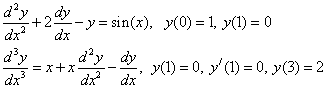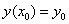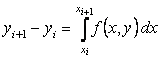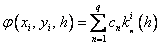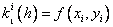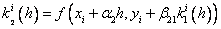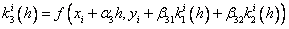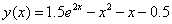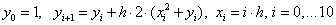Численные методы решения дифференциальных уравнений задача коши

Pers.narod.ru. Обучение. Лекции по численным методам. Численное решение обыкновенных дифференциальных уравнений

5. Численное решение обыкновенных дифференциальных уравнений

Многие задачи науки и техники сводятся к решению обыкновенных дифференциальных уравнений (ОДУ). ОДУ называются такие уравнения, которые содержат одну или несколько производных от искомой функции. В общем виде ОДУ можно записать следующим образом:

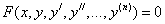
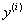
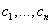
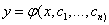
, где x – независимая переменная, — i-ая производная от искомой функции. n — порядок уравнения. Общее решение ОДУ n–го порядка содержит n произвольных постоянных , т.е. общее решение имеет вид .

Для выделения единственного решения необходимо задать n дополнительных условий. В зависимости от способа задания дополнительных условий существуют два различных типа задач: задача Коши и краевая задача. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями. Если же дополнительные условия задаются в более чем одной точке, т.е. при различных значениях независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются краевыми или граничными.

Ясно, что при n=1 можно говорить только о задачи Коши.

Примеры постановки задачи Коши:

Примеры краевых задач:

Решить такие задачи аналитически удается лишь для некоторых специальных типов уравнений.

Численные методы решения задачи Коши для ОДУ первого порядка

Постановка задачи. Найти решение ОДУ первого порядка

на отрезке при условии

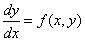
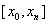
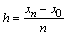
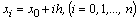
При нахождении приближенного решения будем считать, что вычисления проводятся с расчетным шагом , расчетными узлами служат точки промежутка [x₀, x_n].

Целью является построение таблицы

т.е. ищутся приближенные значения y в узлах сетки.

Интегрируя уравнение на отрезке 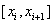, получим

Вполне естественным (но не единственным) путем получения численного решения является замена в нем интеграла какой–либо квадратурной формулой численного интегрирования. Если воспользоваться простейшей формулой левых прямоугольников первого порядка

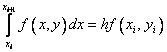
то получим явную формулу Эйлера:

, .

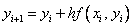
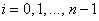
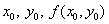
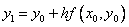
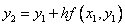
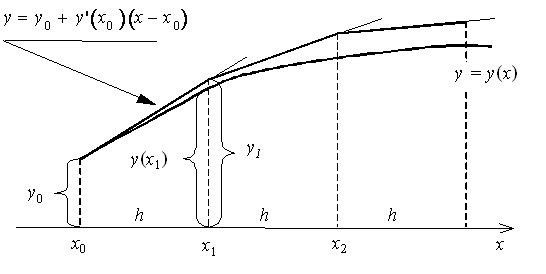
Зная , находим , затем т.д.

Геометрическая интерпретация метода Эйлера:

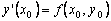
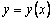
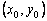
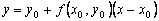
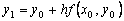
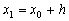
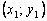
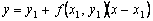
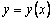
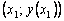
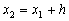
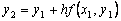
Пользуясь тем, что в точке x₀ известно решение y(x₀) = y₀ и значение его производной , можно записать уравнение касательной к графику искомой функции в точке : . При достаточно малом шаге h ордината этой касательной, полученная подстановкой в правую часть значения , должна мало отличаться от ординаты y(x₁) решения y(x) задачи Коши. Следовательно, точка пересечения касательной с прямой x = x₁ может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую , которая приближенно отражает поведение касательной к в точке . Подставляя сюда (т.е. пересечение с прямой x = x₂), получим приближенное значение y(x) в точке x₂: и т.д. В итоге для i–й точки получим формулу Эйлера.

Явный метод Эйлера имеет первый порядок точности или аппроксимации.

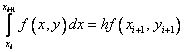
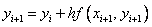
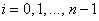
Если использовать формулу правых прямоугольников: , то придем к методу

, .

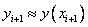
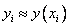
Этот метод называют неявным методом Эйлера, поскольку для вычисления неизвестного значения по известному значению требуется решать уравнение, в общем случае нелинейное.

Неявный метод Эйлера имеет первый порядок точности или аппроксимации.

Модифицированный метод Эйлера: в данном методе вычисление 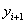состоит из двух этапов:

Данная схема называется еще методом предиктор – корректор (предсказывающее – исправляющее). На первом этапе приближенное значение предсказывается с невысокой точностью (h), а на втором этапе это предсказание исправляется, так что результирующее значение имеет второй порядок точности.

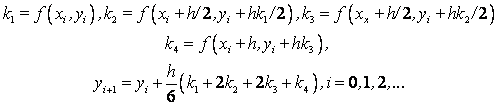
Методы Рунге – Кутта: идея построения явных методов Рунге–Кутты p–го порядка заключается в получении приближений к значениям y(x_i₊₁) по формуле вида

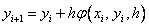
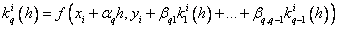
Здесь a_n, b_nj, p_n, 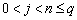– некоторые фиксированные числа (параметры).

При построения методов Рунге–Кутты параметры функции 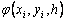(a_n, b_nj, p_n) подбирают таким образом, чтобы получить нужный порядок аппроксимации.

Схема Рунге – Кутта четвертого порядка точности:

Пример. Решить задачу Коши:

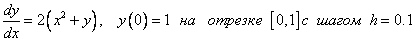
Рассмотреть три метода: явный метод Эйлера, модифицированный метод Эйлера, метод Рунге – Кутта.

Точное решение:

Расчетные формулы по явному методу Эйлера для данного примера:

Расчетные формулы модифицированного метода Эйлера:

Задачи с начальными условиями для систем обыкновенных дифференциальных уравнений

Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений $$ \begin \tag <1>\frac &= f_i (t, u_1, u_2, \ldots, u_n), \quad t > 0\\ \tag <2>u_i(0) &= u_i^0, \quad i = 1, 2, \ldots, m. \end $$

Используя векторные обозначения, задачу (1), (2) можно записать как задачу Коши $$ \begin \tag <3>\frac> &= \pmb(t, \pmb), \quad t > 0, \\ \tag <4>\pmb(0) &= \pmb_0 \end $$ В задаче Коши необходимо по известному решению в точке $ t = 0 $ необходимо найти из уравнения (3) решение при других $ t $.

Численные методы решения задачи Коши

Существует большое количество методов численного решения задачи (3), (4). Вначале рассмотрим простейший явный метод Эйлера и его программную реализацию. Затем будут представлены методы Рунге—Кутта и многошаговые методы.

При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.

Идея численных методов решения задачи (3), (4) состоит из четырех частей:

1. Вводится расчетная сетка по переменной $ t $ (время) из $ N_t + 1 $ точки $ t_0 $, $ t_1 $, $ \ldots $, $ t_ $. Нужно найти значения неизвестной функции $ \pmb $ в узлах сетки $ t_n $. Обозначим через $ \pmb^n $ приближенное значение $ \pmb(t_n) $.

2. Предполагаем, что дифференциальное уравнение выполнено в узлах сетки.

3. Аппроксимируем производные конечными разностями.

4. Формулируем алгоритм, который вычисляет новые значения $ \pmb^ $ на основе предыдущих вычисленных значений $ \pmb^k $, $ k 0 $ при $ \tau\to 0 $.

Явный метод Эйлера

Проиллюстрируем указанные шаги. Для начала введем расчетную сетку. Очень часто сетка является равномерной, т.е. имеет одинаковое расстояние между узлами $ t_n $ и $ t_ $: $$ \omega_\tau = \< t_n = n \tau, n = 0, 1, \ldots, N_t \>. $$

Затем, предполагаем, что уравнение выполнено в узлах сетки, т.е.: $$ \pmb^\prime (t_n) = \pmb(t_n, u(t_n)), \quad t_n \in \omega_\tau. $$

Заменяем производные конечными разностями. С этой целью, нам нужно знать конкретные формулы, как производные могут быть аппроксимированы конечными разностями. Простейший подход заключается в использовании определения производной: $$ \pmb^\prime(t) = \lim_ <\tau \to 0>\frac<\pmb(t+\tau) — \pmb(t)><\tau>. $$

В произвольном узле сетки $ t_n $ это определение можно переписать в виде: $$ \begin \pmb^\prime(t_n) = \lim_ <\tau \to 0>\frac<\pmb(t_n+\tau) — \pmb(t_n)><\tau>. \end $$ Вместо того, чтобы устремлять шаг сетки к нулю, мы можем использовать малый шаг $ \tau $, который даст численное приближение $ u^\prime(t_n) $: $$ \begin \pmb^\prime(t_n) \approx \frac<\pmb^ — \pmb^><\tau>. \end $$ Такая аппроксимация известна как разностная производная вперед и имеет первый порядок по $ \tau $, т.е. $ O(\tau) $. Теперь можно использовать аппроксимацию производной. Таким образом получим явный метод Эйлера: $$ \begin \tag <5>\frac<\pmb^ — \pmb^n> <\tau>= \pmb(t_n, \pmb^). \end $$

Четвертый шаг заключается в получении численного алгоритма. Из (5) следует, что мы должны знать значение $ y^n $ для того, чтобы решить уравнение (5) относительно $ y^ $ и получить формулу для нахождения приближенного значения искомой функции на следующем временном слое $ t_ $: $$ \begin \tag <6>\pmb^ = \pmb^n + \tau \pmb(t_n, \pmb^) \end $$

При условии, что у нас известно начальное значение $ \pmb^0 = \pmb_0 $, мы можем использовать (6) для нахождения решений на последующих временных слоях.

Программная реализация явного метода Эйлера

Выражение (6) может быть как скалярным так и векторным уравнением. И в скалярном и в векторном случае на языке Python его можно реализовать следующим образом

При решении системы (векторный случай), u[n] — одномерный массив numpy длины $ m+1 $ ($ m $ — размерность задачи), а функция F должна возвращать numpy -массив размерности $ m+1 $, t[n] — значение в момент времени $ t_n $.

Таким образом численное решение на отрезке $ [0, T] $ должно быть представлено двумерным массивом, инициализируемым нулями u = np.zeros((N_t+1, m+1)) . Первый индекс соответствует временному слою, а второй компоненте вектора решения на соответствующем временном слое. Использование только одного индекса, u[n] или, что то же самое, u[n, :] , соответствует всем компонентам вектора решения.

Функция euler решения системы уравнений реализована в файле euler.py:

Строка F_ = lambda . требует пояснений. Для пользователя, решающего систему ОДУ, удобно задавать функцию правой части в виде списка компонент. Можно, конечно, требовать чтобы пользователь возвращал из функции массив numpy , но очень легко осуществлять преобразование в самой функции решателе. Чтобы быть уверенным, что результат F будет нужным массивом, который можно использовать в векторных вычислениях, мы вводим новую функцию F_ , которая вызывает пользовательскую функцию F «прогоняет» результат через функцию assaray модуля numpy .

Неявный метод Эйлера

При построении неявного метода Эйлера значение функции $ F $ берется на новом временном слое, т.е. для решении задачи (5) используется следующий метод: $$ \begin \tag <7>\frac<\pmb^ — \pmb^n> <\tau>= \pmb(t_, \pmb^). \end $$

Таким образом для нахождения приближенного значения искомой функции на новом временном слое $ t_ $ нужно решить нелинейное уравнение относительно $ \pmb^ $: $$ \begin \tag <8>\pmb^ — \tau \pmb(t_, \pmb^) — y^n = 0. \end $$

Для решения уравнения (8) можно использовать, например, метод Ньютона.

Программная реализация неявного метода Эйлера

Функция backward_euler решения системы уравнений реализована в файле euler.py:

Отметим, что для нахождения значения u[n+1] используется функция fsolve модуля optimize библиотеки scipy . В качестве начального приближения для решения нелинейного уравнения используется значение искомой функции с предыдущего слоя u[n] .

Методы Рунге—Кутта

Одношаговый метод Рунге—Кутта в общем виде записывается следующим образом: $$ \begin \tag <9>\frac<\pmb^ — \pmb^n> <\tau>= \sum_^s b_i \pmb_i, \end $$ где $$ \begin \tag <10>\pmb_i = \pmb\left( t_n + c_i\tau, \pmb^n + \tau \sum_^s a_\pmb_j \right), \quad i = 1, 2, \ldots, s. \end $$ Формула (9) основана на $ s $ вычислениях функции $ \pmb $ и называется $ s $-стадийной. Если $ a_ = 0 $ при $ j \geq i $ имеем явный метод Рунге—Кутта. Если $ a_ = 0 $ при $ j > i $ и $ a_ \ne 0 $, то $ \pmb_i $ определяется неявно из уравнения $$ \begin \tag <11>\pmb_i = \pmb\left( t_n + c_i\tau, \pmb^n + \tau \sum_^ a_\pmb_j + \tau a_ \pmb_i \right), \quad i = 1, 2, \ldots, s. \end $$ О таком методе Рунге—Кутта говорят как о диагонально-неявном.

Одним из наиболее распространенных является явный метод Рунге-Кутта четвертого порядка: $$ \begin \tag <12>\pmb_1 & = \pmb(t_n, \pmb^n), &\quad \pmb_2 &= \pmb\left( t_n + \frac<\tau><2>, \pmb^n + \tau \frac<\pmb_1> <2>\right),\\ \pmb_3 &= \pmb\left( t_n + \frac<\tau><2>, \pmb^n + \tau \frac<\pmb_2> <2>\right), &\quad \pmb_4 &= \pmb\left( t_n + \tau, \pmb^n + \tau \pmb_3 \right),\\ \frac<\pmb^ -\pmb^n> <\tau>&= \frac<1> <6>(\pmb_1 + 2\pmb_2 + 2\pmb_3 + \pmb_4) & & \end $$

Многошаговые методы

В методах Рунге—Кутта в вычислениях участвуют значения приближенного решения только в двух соседних узлах $ \pmb^n $ и $ \pmb^ $ — один шаг по переменной $ t $. Линейный $ m $-шаговый разностный метод записывается в виде $$ \begin \tag <13>\frac<1> <\tau>\sum_^m a_i \pmb^ = \sum_^ b_i \pmb(t_, \pmb^), \quad n = m-1, m, \ldots \end $$ Вариант численного метода определяется заданием коэффициентов $ a_i $, $ b_i $, $ i = 0, 1, \ldots, m $, причем $ a_0 \ne 0 $. Для начала расчетов по рекуррентной формуле (13) необходимо задать $ m $ начальных значений $ \pmb^0 $, $ \pmb^1 $, $ \dots $, $ \pmb^ $ (например, можно использовать для их вычисления метод Эйлера).

Различные варианты многошаговых методов (методы Адамса) решения задачи с начальными условиями для систем обыкновенных дифференциальных уравнений могут быть получены на основе использования квадратурных формул для правой части равенства $$ \begin \tag <14>\pmb(t_) — \pmb(t_n) = \int_^> \pmb(t, \pmb) dt \end $$

Для получения неявного многошагового метода используем для подынтегральной функции интерполяционную формулу по значениям функции $ \pmb^ = \pmb(t_, \pmb^) $, $ \pmb^n $, $ \dots $, $ \pmb^ $, т.е. $$ \begin \tag <15>\frac<\pmb^ — \pmb^n> <\tau>= \sum_^ b_i \pmb(t_, \pmb^) \end $$

Для интерполяционного метода Адамса (15) наивысший порядок аппроксимации равен $ m+1 $.

Для построения явных многошаговых методов можно использовать процедуру экстраполяции подынтегральной функции в правой части (14). В этом случае приближение осуществляется по значениям $ \pmb^n $, $ \pmb^ $, $ \dots $, $ \pmb^ $ и поэтому $$ \begin \tag <16>\frac<\pmb^ — \pmb^n> <\tau>= \sum_^ b_i \pmb(t_, \pmb^) \end $$

Для экстраполяционного метода Адамса (16) погрешность аппроксимации имеет $ m $-ый порядок.

На основе методов Адамса строятся и схемы предиктор–корректор. На этапе предиктор используется явный метод Адамса, на этапе корректора — аналог неявного метода Адамса. Например, при использовании методов третьего порядка аппроксимации в соответствии с (18) для предсказания решения положим $$ \frac<\pmb^ — \pmb^n> <\tau>= \frac<1> <12>(23 \pmb^ -16\pmb^ + 5\pmb^). $$ Для уточнеия решения (см. (17)) используется схема $$ \frac<\pmb^ — \pmb^n> <\tau>= \frac<1> <24>(9\pmb^ + 19\pmb^ — 5\pmb^ + \pmb^). $$ Аналогично строятся и другие классы многошаговых методов.

Жесткие системы ОДУ

При численном решении задачи Коши для систем обыкновенных дифференциальных уравнений (3), (4) могут возникнуть дополнительные трудности, порожденные жесткостью системы. Локальные особенности поведения решения в точке $ u = w $ передаются линейной системой $$ \begin \frac

= \sum_^ \frac<\partial f_i> <\partial u_j>(t, w) v + \bar(t), \quad t > 0. \end $$
Пусть $ \lambda_i(t) $, $ i = 1, 2, \ldots, m $ — собственные числа матрицы $$ \begin A(t) = \< a_(t) \>, \quad a_(t) = \frac<\partial f_i><\partial u_j>(t, w). \end $$ Система уравнений (3) является жесткой, если число $$ \begin S(t) = \frac <\max_<1 \leq i \leq m>|Re \lambda_i(t)|> <\min_<1 \leq i \leq m>|Re \lambda_i(t)|> \end $$ велико. Это означает, что в решении присутствуют составляющие с сильно различающимися масштабами изменения по переменной $ t $.
Для численное решения жестких задач используются вычислительные алгоритмы, которые имеют повышенный запас устойчивости. Необходимо ориентироваться на использование $ A $-устойчивых или $ A(\alpha) $-устойчивых методов.
Метод называется $ A $-устойчивым, если при решении задачи Коши для системы (3) область его устойчивости содержит угол $$ \begin |\arg(-\mu)| —>
Численные методы решения задачи Коши
Основные понятия и определения
Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную [math]x[/math] , неизвестную функцию [math]y(x)[/math] этой независимой переменной и ее производные [math]y'(x),y»(x),\ldots,y^<(n)>(x)\colon[/math]
где [math]F(x,y, y’,\ldots,y^<(n)>)[/math] — функция указанных аргументов, заданная в некоторой области их изменения.
Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.
Если в соотношении (6.1) функция [math]F[/math] такова, что его можно представить в виде
то уравнение называется обыкновенным дифференциальным уравнением л-го порядка, разрешенным относительно старшей производной.
Уравнение называется линейным, если функция [math]f[/math] линейна относительно искомой функции и ее производных, т.е. если уравнение может быть записано в виде
где [math]a_n(x),a_(x),\ldots,a_0(x),f(x)[/math] — известные в общем случае нелинейные функции от [math]x[/math] .
Решением дифференциального уравнения n-го порядка называется функция [math]y(x)[/math] , непрерывная на некотором интервале [math](a,b)[/math] вместе со своими производными до [math](n-1)[/math] порядка включительно, имеющая производную [math]y^<(n)>(x)[/math] и такая, что подстановка [math]y(x)[/math] в уравнение обращает его в тождество.
График решения дифференциального уравнения называется интегральной кривой.
Одной из важнейших задач в теории и приложениях дифференциальных уравнений является задана Коши (начальная задана), в которой требуется найти решение дифференциального уравнения, удовлетворяющее заданным начальным условиям. Для уравнения (6.2) она записывается следующим образом:
где [math]x_0\in (a,b),
y_0,y’_0,\ldots,y_0^<(n-1)>[/math] — заданные числа.
Теорема 6.1 (о существовании и единственности решения задачи Коши (6.4)). Пусть выполнены следующие условия:
а) функция [math]f(x,y,\ldots,y^<(n-1)>)[/math] определена и непрерывна в некоторой замкнутой области [math]\overline[/math] , а также имеет в [math]\overline[/math] ограниченные частные производные по переменным [math]y,y’,\ldots,y^<(n-1)>[/math] ;
б) точка [math](x_0,y_0,y’_0,\ldots,y_0^<(n-1)>)[/math] лежит внутри области [math]\overline[/math] .
Тогда решение задачи Коши (6.4) существует и единственно.
Общим решением дифференциального уравнения л-го порядка в области [math]G\subset \overline[/math] ( [math]\overline[/math] — область, в которой выполнены условия теоремы 6.1) называется функция [math]y=y(x,C_1,\ldots,C_n)[/math] , зависящая от [math]n[/math] произвольных постоянных, и такая, что при подстановке в уравнение она обращает его в тождество при любых значениях [math]C_1,\ldots,C_n[/math] . Геометрически общее решение в области [math]G[/math] представляет собой семейство непересекающихся интегральных кривых, полностью покрывающих всю область.
Общим интегралом дифференциального уравнения называется соотношение вида [math]\varphi(x,y,C_1,\ldots,C_n)=0[/math] , неявно определяющее общее решение.
При конкретных значениях [math]C_1,\ldots,C_n[/math] , включая [math]\pm\infty[/math] , из общего решения выделяется частное решение, а общий интефал становится частным интегралом. В каждой точке [math](x,y)[/math] частного решения или частного интефала выполняются условия теоремы 6.1.
Наряду с проблемой решения дифференциальных уравнений л-го порядка на практике возникает проблема решения систем обыкновенных дифференциальных уравнений первого порядка, связывающих независимую переменную [math]x[/math] , неизвестные функции [math]y_1(x),\ldots, y_n(x)[/math] и их производные [math]y’_1(x),\ldots, y’_n(x)[/math] .
В случае, если уравнения разрешимы относительно производных, систему можно записать в нормальной форме Коши (где [math]f_i(x,y_1,\ldots,y_n),
i=\overline<1,n>[/math] — известные функции):
Решением системы (6.5) называется совокупность [math]n[/math] функций [math]y_1(x),\ldots, y_n(x)[/math] , непрерывных на некотором интервале (д,6), такая, что подстановка этих функций в (6.5) обращает все уравнения в тождества.
Задача Коши для системы (6.5) состоит в нахождении решения системы, удовлетворяющего начальным условиям (где [math]y_<1\,0>,y_<2\,0>,\ldots,y_[/math] — известные числа):
В векторной форме задача Коши (6.5),(6.6) имеет вид
F(x,Y)= \bigl(f_1(x,Y),\ldots, f_n(x,Y)\bigr)^T,
Теорема 6.2 (о существовании и единственности решения задачи Коши (6.5),(6.6)). Пусть выполнены следующие условия:
а) функции [math]f_i(x,y_1,\ldots,y_n),
i=\overline<1,n>[/math] , определены и непрерывны в некоторой замкнутой области [math]\overline[/math] , а также имеют в [math]\overline[/math] ограниченные частные производные по переменным [math]y_1,\ldots,y_n[/math] ;
б) точка [math](x_0,y_<1\,0>,y_<2\,0>,\ldots,y_)[/math] лежит внутри области [math]\overline[/math] .
Тогда решение задачи Коши (6.5),(6.6) существует и единственно.
1. Во многих практических приложениях независимая переменная обозначается через [math]t[/math] и имеет смысл времени, поэтому задача Коши называется начальной задачей.
2. Понятия общего и частного решений, общего и частного интегралов для уравнения первого порядка и систем совпадают по форме, если заменить функцию [math]y(x)[/math] на вектор-функцию [math]Y(x),
f(x,y)[/math] на [math]F(x,Y)[/math] , а [math]y_0[/math] — на [math]Y_0[/math] .
Численные методы, рассматриваемые в данном разделе, пригодны для решения задач Коши, записанных в форме (6.5),(6.6). Чтобы решить задачу Коши (6.4) этими методами, ее необходимо привести к системе [math]n[/math] уравнений первого порядка, т.е. к виду (6.5),(6.6).
y_n(x)= y^<(n-1)>(x)[/math] , получаем
Получим точное решение модельного примера, используемого далее для демонстрации применения различных численных методов.
Пример 6.1. Найти аналитическое решение задачи Коши [math]Ty’+y=1,
y(0)=0[/math] , где 0″>[math]T>0[/math] — известное число, называемое постоянной времени.
Решение задачи Коши найдем с помощью известной методики.
1. Определим общее решение однородного уравнения [math]Ty’+y=0[/math] . Поскольку корень [math]\lambda=-1\!\!\not<\phantom<|>>\,T[/math] соответствующего характеристического уравнения [math]T\lambda+1=0[/math] действительный, то [math]y_0(x)=Ce^<\lambda x>= Ce^<-x\!\not<\phantom<|>>\,\,T>[/math] — общее решение однородного уравнения.
2. Частное решение неоднородного уравнения ищется в форме [math]y_<\text>=A[/math] , где [math]A=\text[/math] . После подстановки в решаемое уравнение получаем [math]y_<\text>=1[/math] .
3. Общее решение неоднородного уравнения получается как сумма общего решения однородного уравнения и частного решения неоднородного уравнения:
Ему соответствует семейство интегральных кривых, характеризующееся параметром [math]C[/math] , который может принимать произвольные значения.
4. Частное решение неоднородного уравнения находим из начального условия: [math]y(0)=C+1=0[/math] . Отсюда [math]C=-1[/math] и [math]y(x)=1-e^<-x\!\not<\phantom<|>>\,\,T>[/math] .
Пример 6.2. Записать дифференциальное уравнение второго порядка [math]2y»+y’+4y=6\sin,
y'(0)=2[/math] , в виде системы дифференциальных уравнений в нормальной форме Коши.
Введем обозначения: [math]y_1(x)=y(x),
y_2(x)=y’_1(x)[/math] и запишем уравнение в форме [math]y»=-\frac<1><2>y’-2y+3\sin[/math] , разрешенной относительно старшей производной. Тогда получим
Численные и приближенно-аналитические методы решения задачи Коши в отличие от аналитических методов позволяют найти искомую функцию [math]y(x)[/math] лишь приближенно. Но при этом численные методы являются более универсальными, так как с их помощью можно приближенно решать многие из задач, точные решения которых аналитическими методами не могут быть найдены. Аналитическими методами в основном решаются только линейные задачи и некоторые типы нелинейных задач, в то время как для численных методов эти ограничения отсутствуют.
Чтобы упростить изложение и в силу того, что численные методы легко обобщаются на системы уравнений, в дальнейшем будем рассматривать решение задачи Коши для уравнения первого порядка
Численное решение задачи ищется в узлах сетки [math]\Omega_n= \[/math] , где [math]h_=x_-x_,
i=\overline<0,n-1>[/math] — расстояние между соседними узлами, называемое шагом интегрирования (параметром сетки). Если [math]h_=h=\text[/math] , сетка называется равномерной (регулярной), а если [math]h_=\text[/math] — неравномерной (нерегулярной). В случае равномерной сетки узлы находятся по формуле [math]x_= x_0+ih,
i=\overline<0,n>[/math] , а в случае неравномерной (где [math]\delta_= \frac>>[/math] — параметр нерегулярности):
Решение находится в виде последовательности значений [math]\widehat_0,\widehat_1, \widehat_2,\ldots, \widehat_n[/math] , являющихся приближением значений [math]y_0,y(x_1),y(x_2),\ldots,y(x_n)[/math] точного решения [math]y(x)[/math] в узлах сетки [math]\Omega_[/math] (рис. 6.1).
Сеточное представление [math]y(x_i),
i=\overline<0,n>[/math] , известной функции [math]y(x)[/math] (точного решения задачи Коши) называется проекцией [math]y(x)[/math] на сетку [math]\Omega_n[/math] .
Дискретные и непрерывно-дискретные методы
Численные методы решения обыкновенных дифференциальных уравнений делятся на две группы:
– дискретные методы , позволяющие найти решение только в узлах сетки. Эти методы называются еще разностными методами или методами сеток;
– непрерывно-дискретные методы , основанные на использовании дискретных методов и сплайн-функций для восполнения численных результатов. Они позволяют найти непрерывные решения дифференциальных уравнений.
Дискретные методы (методы сеток) подразделяются на явные и неявные. Значение [math]\widehat_[/math] , на (i+1)-м шаге может определяться явно:
где [math]\Phi(.)[/math] — некоторая функция, зависящая от конкретного метода (кроме последней рассчитанной точки [math](x_,\widehat_)[/math] могут использоваться еще [math](k-1)[/math] предыдущих точек), или неявно:
где искомая величина [math]\widehat_[/math] входит одновременно и в левую, и в правую часть.
Явные и неявные методы делятся также на одношаговые и многошаговые (k-шаговые). В одношаговых методах для расчета очередной точки [math](x_,\widehat_)[/math] требуется информация только о последней рассчитанной точке [math](x_,\widehat_)[/math] . В k-шаговых методах для нахождения точки [math]x_,\widehat_[/math] требуется информация о [math]k[/math] предыдущих точках (рис. 6.2).
Формулы (6.10),(6.11) в общем случае представляют собой нелинейные уравнения относительно [math]\widehat_[/math] и называются разностными схемами.
Численный алгоритм (метод) называется устойчивым, если численные результаты непрерывно зависят от входных данных и если погрешность остается ограниченной при заданных пределах изменения параметров численного алгоритма (шагов сетки, числа итераций и др.).
Сходимость приближенных методов является основной проблемой, от успешного преодоления которой зависит точность решения всей задачи. Численный алгоритм называется сходящимся, если при стремлении его параметров к определенным предельным значениям, например, при [math]h\to0[/math] (или при [math]s\to\infty[/math] , где [math]s[/math] — число итераций), результаты стремятся к точному решению.
При известном точном решении некоторой модельной задачи сходимость может быть проверена следующим образом. Фиксируется некоторая точка x_0″>[math]x>x_0[/math] и строится последовательность сеток [math]\Omega_[/math] , таких, что [math]h\to0,[/math] [math]x=x_= x_<0>+nh[/math] . Здесь для простоты считаем, что все сетки, образующие указанную последовательность, являются равномерными. Тогда, если [math]|\widehat_-y(x_)|\to0[/math] при [math]h\to0
(n\to\infty)[/math] , то метод является сходящимся в точке [math]x[/math] . Если метод сходится в каждой точке [math]x\in[c,d]\subset (a,b)[/math] , то он сходящийся на [math][c,d][/math] .
Локальная и глобальная ошибки
Локальной ошибкой численного метода на (i+1) -м шаге называется величина
где [math]y(x_)[/math] — значение точного решения при [math]x=x_[/math] , а [math]\widehat_[/math] — приближенное решение, получаемое по формуле (6.10) или (6.11) при условии, что вместо приближенных значений [math]\widehat_, \widehat_,\ldots, \widehat_[/math] используются значения, соответствующие точному решению, т.е. [math]y(x_), y(x_),\ldots, y(x_)[/math] .
Глобальной ошибкой называется величина [math]e_(h)= \widehat_-y(x_)[/math] , где [math]\widehat_[/math] — значение, получаемое по формулам (6.10) или (6.11) при [math]i=n-1[/math] .
Глобальная ошибка определяется:
а) ошибками округления и ошибками арифметических действий, обусловленными числом разрядов компьютера и характером выполняемых операций для расчета значения искомой функции в очередной точке [math]x_[/math] ;
б) методическими ошибками, определяемыми выбранным алгоритмом;
в) переходными ошибками, обусловленными тем, что при расчете значения р/+1 вместо точных значений [math]y(x_), y(x_),\ldots, y(x_)[/math] берутся приближенные значения [math]\widehat_, \widehat_,\ldots, \widehat_[/math] , полученные на предыдущих шагах.
Локальные ошибки «переносятся» в точку [math]x_n[/math] и формируют глобальную ошибку.
Число [math]p[/math] называется порядком (точностью) численного метода, если его глобальная ошибка есть [math]O[/math] большое от [math]h^p[/math] , то есть [math]e_n(h)= O(h^p)[/math] .
На практике в качестве характеристики точности метода часто используется величина [math]\varepsilon(h)= \max_\bigl|\widehat_-y(x_)\bigr|[/math] .
Рассмотрим введенные понятия более подробно на примере явных одношаговых методов, построенных для задачи (6.9). При этом формулу (6.10) представим в виде
где [math]\Psi(\widehat_,x_,h)[/math] — некоторая функция, определяемая конструкцией того или иного метода.
Обозначим [math]y(x,x_,\widehat_)[/math] — решение задачи Коши [math]u’=f(x,u),
u(x_)= \widehat_[/math] . Тогда локальная ошибка определяется выражением
Геометрическая интерпретация возникновения локальных и глобальной ошибок изображена на рис. 6.3.
Можно показать, что если локальная ошибка имеет порядок [math](p+1)[/math] , то есть [math]\varepsilon_(h)= O(h^)[/math] , то глобальная погрешность имеет на единицу меньший порядок, т.е. [math]e_(h)= O(h^p)[/math] .
Перейдем теперь к рассмотрению устойчивости численных методов. Она проверяется на «тестовом примере»
где [math]\mu[/math] — в общем случае комплексная константа. Дифференциальное уравнение в (6.12) является простейшим линейным уравнением, и для него можно получить значимые критерии устойчивости в явной форме.
Устойчивость методов решения задачи Коши
Метод называется устойчивым (ограниченно устойчивым), если существует такое число 0″>[math]h_<\text>>0[/math] , что при использовании метода для решения задачи (6.12), где [math]\operatorname\mu , с шагом [math]0 при [math]i\to\infty[/math] глобальная ошибка ограничена. Величина [math]h_<\text>[/math] называется критическим шагом. Если h_<\text>»>[math]h>h_<\text>[/math] , глобальная ошибка может неограниченно возрастать.
В ограниченно устойчивых методах при задании величины шага [math]h[/math] необходимо учитывать значение критического шага [math]h_<\text>[/math] . Для сложных дифференциальных уравнений и систем нахождение [math]h_<\text>[/math] является самостоятельной задачей, а свойство ограниченной устойчивости предупреждает вычислителя о возможных проблемах. Поэтому на практике становится актуальной задача конструирования таких методов, которые были бы устойчивы при любом значении шага, а его величина выбиралась бы только исходя из желаемой точности расчетов (при этом класс решаемых задач может быть ограничен).
Метод называется A-устойчивым , если при его применении с любым фиксированным положительным шагом [math]h[/math] все численные решения задачи (6.12) с комплексной константой [math]\mu
(\operatorname\mu стремятся к нулю при [math]i\to\infty[/math] .
Область A-устойчивости — совокупность значений [math]h[/math] и [math]\mu[/math] , удовлетворяющих условию [math]\operatorname(h\mu) . Она изображена на рис. 6.4,а. Выполнение свойства A-устойчивости является желательным, поскольку если решение задачи (6.12) асимптотически устойчиво (в силу условия [math]\operatorname\mu корень характеристического уравнения находится в левой полуплоскости), то погрешность численного решения стремится к нулю при любой величине шага 0″>[math]h>0[/math] .
При исследовании устойчивости численного метода необходимо использовать соответствующую ему разностную схему для решения задачи (6.12) и привести ее к линейному разностному уравнению с постоянными коэффициентами:
Известно, что критерием устойчивости решения линейного разностного уравнения является требование расположения корней [math]\lambda_[/math] соответствующего характеристического уравнения [math]a_n \lambda^n+ a_\lambda^+ \ldots+a_0=0[/math] внутри круга единичного радиуса с центром в начале координат, т.е.
1. Численные методы, которые можно представить в виде (где | [math]|\alpha_0|+|\beta_0|\ne0,
f_= f(x_, \widehat_)[/math] называются линейными k-шаговыми методами)
\sigma(\xi)= \sum\limits_^ \beta_\xi^>[/math] . Линейный многошаговый метод является устойчивым, если для фиксированного значения [math]h\mu[/math] корни уравнения
лежат внутри круга единичного радиуса с центром в начале координат.
2. Для ограниченно устойчивых методов важной задачей является нахождение величины критического шага [math]h_<\text>[/math] . Если константа [math]\mu[/math] в уравнении (6.12) действительная, то можно найти интервал устойчивости .
3. Существуют определения, смягчающие свойство A-устойчивости. Приведем одно из них. Метод называется A(α)-устойчивым, [math]\alpha\in(0,\pi\!\!\not<\phantom<|>>\,2)[/math] , если при его применении все численные решения уравнения (6.12) с фиксированным положительным шагом [math]h[/math] стремятся к нулю при [math]i\to\infty[/math] для всех [math]\mu[/math] , удовлетворяющих условию [math]|\arg(-\mu)| , где [math]\arg(-\mu)[/math] — аргумент комплексного числа [math](-\mu)[/math] . Область A(α)-устойчивости показана на рис. 6.4,5. Это условие применимо и для линейных систем с постоянными коэффициентами [math]y’=Ay[/math] , где [math]A[/math] — матрица коэффициентов, имеющая собственные значения [math]\lambda_,
i=\overline<1,n>[/math] . Геометрическая интерпретация изображена на рис. 6.4,в.
4. Можно показать, что явные линейные многошаговые методы не могут быть A-устойчивыми.

источники:
http://slemeshevsky.github.io/num-mmf/ode/html/._ode-FlatUI001.html
http://mathhelpplanet.com/static.php?p=chislennyye-metody-resheniya-zadachi-koshi