Численные методы решения эволюционных функционально-дифференциальных уравнений Текст научной статьи по специальности « Математика»
Аннотация научной статьи по математике, автор научной работы — Жуковская Татьяна Владимировна, Молоканова Елена Анатольевна
Рассматривается общий метод приближенного решения задачи Коши для функционально-дифференциального уравнения эволюционного типа. На основании общего метода получены аналоги классических методов Эйлера и Рунге-Кутты для численного решения функционально-дифференциальных уравнений . Приведены условия сходимости методов
Похожие темы научных работ по математике , автор научной работы — Жуковская Татьяна Владимировна, Молоканова Елена Анатольевна
NUMERICAL METHODS FOR SOLUTION OF EVOLUTIONARY FUNCTIONAL-DIFFERENTIAL EQUATIONS
General method for construction of approximate solution to the Cauchy problem for evolutionary functional-differential equation is described. Analogs of the Euler method and the Runge-Kutta method for numerical methods of solution of evolutionary functional-differential equations are given on the basis of this method. Conditions for convergence of methods are presented.
Текст научной работы на тему «Численные методы решения эволюционных функционально-дифференциальных уравнений»
УДК 517.988.6, 519.62
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЭВОЛЮЦИОННЫХ ФУНКЦИОНАЛЬНО-ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
© Т. В. Жуковская, Е. А. Молоканова
Ключевые слова: вольтерров оператор; т -вольтерров оператор; функционально-дифференциальное уравнение; задача Коши; приближенное решение; численные методы. Рассматривается общий метод приближенного решения задачи Коши для функционально-дифференциального уравнения эволюционного типа. На основании общего метода получены аналоги классических методов Эйлера и Рунге-Кутты для численного решения функционально-дифференциальных уравнений. Приведены условия сходимости методов.
Функционально-дифференциальные уравнения описывают многочисленные процессы в физике, технике, экономике, медицине и т. д. Найти «точное» решение таких уравнений можно только в исключительных случаях, поэтому особенно актуальной является задача приближенного решения функционально-дифференциальных уравнений. В работах 1 для линейного уравнения рассматриваются методы приближенного построения функции Коши, основанные на построении обратного оператора и аппроксимации ядра оператора ступенчатыми функциями. Ряд работ посвящен численным методам решений специальных типов функционально-дифференциальных уравнений 7: с авторегулируемым запаздыванием, нейтрального типа, интегро-дифференциальным и др. В случае, когда решение дифференциального уравнения не продолжаемо на весь отрезок [a, b] и имеет вертикальную асимптоту, в [10, 11] предлагается модификация метода Эйлера для численного построения решения.
В настоящей работе предлагается общий подход к построению численных методов решения уравнения
Здесь оператор F : ACp[a,b] ^ Lp[a,b] является вольтерровым [12], т. е.
Vy £ [0,b — a] Vxi, x2 £ ACp[a, b]
(xi(t) = X2(t) Vt £ [a,a + 7]) ^ ((Fxi)(t) = (Fx2)(t) Vt £ [a,a + 7]).
Свойство вольтерровости оператора F позволяет рассматривать решение данного уравнения, определенное не на всем [a, b] , а на его части — отрезке [a,a + 7] , 7 £ (0, b — a), и определить понятие продолжения решения. Вот почему уравнение с вольтерровым оператором F называют эволюционным [13]. Предлагаемые численные методы решения такого уравнения используют специфику вольтеррового оператора F и являются эволюционными в том смысле, что значение решения вычисляются постепенно при все больших значениях аргументов. Таким свойством обладают, например, известные методы решения обыкновенных дифференциальных уравнений (методы Эйлера, Рунге-Кутты, Адамса).
1. Метод Тонелли
На примере метода Тонелли, известного для обыкновенных дифференциальных уравнений (см., например, [14]), удобно проследить основную идею многих эволюционных методов приближенного решения уравнений с последействием.
Рассмотрим задачу Коши
X(t) = (GHx)(t), t £ [a,b], x(a) = а. (1)
Здесь операторы H : ACp[a,b] ^ Lr[a,b], G : Lr[a,b] ^ Lp[a,b] вольтерровы. Разобьем
отрезок [a,b] на к равновеликих частей точками a, a + Tk, a + 2r^, b (тk = )■
Алгоритм состоит в замене оператора H оператором Hk : ACp[a,b] ^ Lr[a,b] ,
Вследствие т -вольтерровости оператора Hk решение Xk задачи
Xk(t) = (GHkXk)(t), t £ [a,b], Xk(a) = а, (2)
находится по формулам
xk(t) = а + f(G0)(s)ds, если t £ [a,a + Tk];
Xk(t) = (xk)(a + iTk)+ f (GHkXk)(s)ds, (3)
если t £ [a + iTk,a + (i + 1)Tk], i = 0, 1. k — 1.
Достаточные условия сходимости метода Тонелли предоставляет следующее утверждение.
Теорема 1. Пусть операторы H : ACp[a, b] ^ Lr [a, b], G : Lr [a, b] ^ Lp[a, b] непрерывны, ограничены и хотя бы один из них является вполне непрерывным. Пусть, далее, для решений Xk задач (2) при любом к выполнено неравенство \\Xk\\acv х1 при І£ [tl,t2),
х2 = х1 + / (Тyl)(s)ds,
хі = хі-1 + / (ТУі-1 )(,з)сІ,в. ІІ— 1
Пример 1. Найдем приближенное решение задачи
х(Ь) = х2(-) — 4 + 1, Ье [0,1], х(0) = 0. (8)
Предварительно проверим выполнение условий теоремы 2. Оператор Т, определяемый равенством (Ту)(Ь) = у2(|) —14 + 1, переводит каждое ограниченное множество пространства 1^2р[а,Ъ] в ограниченное множество пространства Ьр[а,Ъ] и непрерывен [15]. Из результатов работы [16] следует однозначная разрешимость задачи (8). Сравним точное решение задачи (8) х = Ь с приближенным решением, найденным по формулам (7). Возьмем к = 10, т = 0,1, получим
х1 = (—— + 1)dі = 0, 0999,
х2 = 0, 0999 + (-— + 1)dі = 0,1993,
хз = 0,1993 + (0, 09992 — — + 1)dі = 0, 3078,
х10 = 0, 9034 + (0, 80432 — 4 + 1^і = 0, 9980.
Теперь применим формулу (7) к численному интегрированию задачи Коши для обыкновенного дифференциального уравнения
х(Ь) = /(Ь,х(Ь)), Ь Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Хг = Х—1 + J / (8,Хг-г)“8, I = 1, 2. к.
Если функция / : [а,Ь] х Я ^ Я непрерывна по совокупности аргументов, то для вычисления интегралов можно воспользоваться методом прямоугольников. Тогда
Хг = Хг-1 + Тк ■ /(г-1, Хг-1), г = 1,2,к.
Таким образом, в применении к обыкновенному дифференциальному уравнению предлагаемый метод аналогичен известному методу Эйлера.
Отметим, в заключение, что если для любого х Е АСр[а, Ь] функция (ТРкх)(Ь) кусочно
непрерывна на интервале (Ьг-1,Ьг), то интеграл в формуле (7) можно вычислить прибли-
женно методом прямоугольников. В этом случае получаем
Хг = Хг-1 + Тк ■ (Ту-Щ-г). (9)
3. Улучшенный метод Эйлера
В основе рассмотренных методов лежит идея замены задачи Коши (5) «приближенной задачей», эквивалентной уравнению с т -вольтерровым оператором. Эту идею применим для распространения методов Рунге-Кутты на решение функционально-дифференциальных уравнений. Выведем формулу улучшенного метода Эйлера (метода Рунге-Кутты второго порядка). Для приближенного решения задачи (5) заменим ее задачей
Хк(Ь) = (Т[Ркх + ТкТРкх])(Ь), Ь Е [а, Ь], х(а) = а. (10)
Здесь оператор Тк : Ьр[а,Ь] ^ Ьг [а,Ь] определяется равенством (Тку)(Ь) = / Тк(Ь, 8)у(з)й8,
%(Ь,8) = ( 1 если [— ]тк + а -8 к
Хг+1 = Хг + J /(8,Хг + J /(£,Хг)“£)“,8.
= Хг + / / (8,Хг + J / (t,xг
Будем предполагать, что функция / : [а, Ь] х Я ^ Я непрерывна по совокупности аргументов. Для вычисления интегралов воспользуемся методом прямоугольников. Тогда
Хг+г = Хг + Тк ■ /(Ьг + 0, 5тк,хг + 0, 5тк/(Ьг,хг)).
Таким образом, для обыкновенных дифференциальных уравнений формула (11) является формулой улучшенного метода Эйлера.
Пусть для любого х Е АСР [а,Ь] функция (ТРкх)(Ь) кусочно непрерывна на интервале (и,и+\). В этом случае определенные интегралы в формуле (11) можно приближенно вычислить с помощью метода прямоугольников. Тогда решение задачи (10) запишется в виде
у0(8) = а, у0(8) = а + 0, 5тк(Ту0)(а), 8Е [а,Ьг],
Хг = а + Тк(Ту0)(а + 0, 5тк);
(8) = \ Уг-г(8), если 8 Е [a,tг],
\ Хг, если 8 Е (и,к+г],
уг-г(8), если 8Е [а,Ьг], (12)
уг(8 1 хг + 0, 5тк(Туг)(Ьг), если 8Е (Ьг,Ьг+г],
Хг+г = хг + Тк(Туг)(Ьг + 0, 5тк).
Пример 2. Применим формулы метода Эйлера и улучшенного метода Эйлера для численного решения задачи
Х(Ь) = 4у х ^2^ — 2, Ь £ [0,1], х(0) = 1.
Эта задача имеет единственное решение х = (Ь + 1)2. Вычисления будем производить по формулам (9) и (12), взяв к = 10, т = 0,1.
Ь£ [0; 0,1] хх = 1 + 0,1 (4л/1 — 2) = 1,2; t £ (0,1; 0,2] Х2 = 1,2 + 0,1 (4^1 — 2) = 1,4;
t £ (0,2; 0,3] Хз = 1,4 + 0,1 (4^1,2 — 2) = 1,638.
И т. д., полностью результаты счета приведены в табл. 1.
2. Улучшенный метод Эйлера.
Уо(з) = 1, уо(з) = 1 + 0,05 (4у/1 — 2) = 1,1; 5£ [0; 0,1],
Хх = 1 + 0,1 (4^/1Д — 2) ^ 1,2195;
Ух(в)^ 1,2195; у1(в) = 1,2195 + 0,05 (4л/1 — 2) = 1,3195; ¿£ [0,1; 0,2),
Х2 = 1,2195 + 0,1 (4^1! — 2)^ 1,4390;
У2(в) = 1, 4390; у2(в) = 1,4390 + 0,05 (4^/ 1,2195 — 2)^ 1,5598; й£ [0,2; 0,3),
уз = 1,4390 + 0,1 (4^1,3195 — 2) = 1,6985.
И т. д., полностью результаты вычислений приведены в табл. 1.
Решение задачи Х(Ь) = 4 у х ^2^ — 2 , t £ [0, 1] , х(0) = 1, методом Эйлера и улучшенным методом Эйлера
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
Метод Эйлера 1,200 1,400 1,638 1,838 2,111 2,385 2,697 3,009 3,351 3,693
метод Эйлера 1,2195 1,4390 1,6985 1,9580 5 5 ,2 2, 2,5571 6 6 9 ,8 2, 1 6 3 ,2 3, 3,6155 3,9948
Точное решение 1,21 1,44 1,69 1,96 2,25 2,56 2,89 3,24 3,61 4,00
1 . Азбелев Н.В., Смолин И.М., Цалюк З.Б. Об одном приближенном методе построения функции
Коши // Доклады АН СССР. 1960. Т. 135. № 3. С. 511-514.
2 . Жуковская ТВ, Жуковский Е.С. Формула для вычисления значений функции Коши //
Функц. дифференц. уравнения и их приложения. Пермь: Изд-во Пермского политехн. ин-та, 1988. С. 34.
3 . Жуковская Т.В. Интерполяция функции Коши // Вестник Тамбовского университета. Серия
Естественные и технические науки. Тамбов, 2002. Т. 7. Вып. 1. С. 110-111.
4 . Жуковская Т.В. Метод построения функции Коши уравнения с обобщенно вольтерровым опе-
ратором // Вестник Тамбовского университета. Серия Естественные и технические науки. Тамбов, 2003. Т. 8. Вып. 1. С. 162-163.
5 . Юганова С.А. К вопросу о приближенном построении оператора Коши. Пермь, 1981. 11 с.
Деп. в ВИНИТИ, № 3820-81.
6 . Жуковская Т.В. О приближенных методах решения задачи Коши // Современ. методы теории
краев. задач. Воронеж: Изд-во Воронежского гос. ун-та, 2005. С. 59.
7. Жуковская ТВ, Жуковский Е.С. Численные методы решения функциональнодифференциальных уравнений // Функц. дифференц. уравнения. Пермь: Изд-во Пермского политехн. ин-та, 1988. С. 110-113.
8 . Жуковская Т.В, Жуковский Е.С. Об уравнении Риккати // Современные проблемы механики
и прикладной математики. Воронежская математическая школа. Воронеж, 1998. С.116.
9 . Драхлина Н.Ш. О сходимости одного приближенного метода решения функционально-
дифференциального уравнения // Краевые задачи. Пермь: Изд-во Перм. политех. ин-та, 1988. С. 82-87.
10 . Жуковский Е.С. О параметрическом задании решения дифференциального уравнения и его
приближенном нахождении // Известия ВУЗов. Математика. 1995. № 4 (407). С. 31-34.
11 . Жуковская Т.В, Молоканова Е.А., Стуров Д.Л. О вертикальных асимптотах интегральных
кривых обыкновенных дифференциальных уравнений // Вестник Тамбовского гос. техн. ун-та. Тамбов, 2011. Т. 17. № 3. С. 744-751.
12 . Тихонов А.Н. О функциональных уравнениях типа Вольтерра и их применениях к некоторым
задачам математической физики // Бюл. Москов. ун-та. Секц. А. 1938. Т. 1. Вып. 8. С. 1-25.
13 . Азбелев Н.В., Березанский Л.М., Рахматуллина Л.Ф. О линейном функционально-
дифференциальном уравнении эволюционного типа // Дифференциальные уравнения. 1977. Т. 13. № 11. С. 1915-1925.
14 . Мамедов Я.Д. Приближенные методы решения обыкновенных дифференциальных уравнений.
Баку: МААРИФ, 1974. 176 с.
15 . Данфорд Н., Шварц Дж. Линейные операторы. Общая теория. М: Едиториал УРСС, 2004.
16 . Азбелев Н.В., Максимов В.П. Априорные оценки решений задачи Коши и разрешимость кра-
евых задач для уравнений с запаздывающим аргументом // Дифференциальные уравнения. 1979. Т. 15. № 10. С. 1731-1749.
БЛАГОДАРНОСТИ: Работа выполнена при поддержке РФФИ (проект № 11-01-00645) и Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России на 2009-2013 годы».
Поступила в редакцию 28 сентября 2012 г.
Zhukovskaya T.V., Molokanova E.A. NUMERICAL METHODS FOR SOLUTION OF EVOLUTIONARY FUNCTIONAL-DIFFERENTIAL EQUATIONS
General method for construction of approximate solution to the Cauchy problem for evolutionary functional-differential equation is described. Analogs of the Euler method and the Runge-Kutta method for numerical methods of solution of evolutionary functional-differential equations are given on the basis of this method. Conditions for convergence of methods are presented.
Key words: Volterra operator; t-Volterra operator; functional-differential equation; Cauchy problem; approximate solution; numerical methods.
Лекция «Численные методы решения уравнений»
учебно-методический материал
Лекция по разделу «Численные методы».
Рассматриваются следующие методы решения алгебраических и трансцендентных уравнений:
1) метод дихотомии (метод деления отрезка пополам),
3) метод касательных,
4) метод итераций.
Скачать:
| Вложение | Размер |
|---|---|
| численные методы решения уравнений | 87 КБ |
Предварительный просмотр:
Тема 12.2.Приближенное решение алгебраических и трансцендентных уравнений.
Задача о нахождении приближенных значений действительных корней уравнения f(x)=0 предусматривает предварительное отделение корня , т.е. установления промежутка, в котором других корней данного уравнения нет.
Будем предполагать, что функция f(x) в промежутке [a; b] непрерывна вместе со своими производными f’(x) и f’’(x) , значения f(а) и f(b) функции на концах промежутка имеют разные знаки, т.е. f(а) ∙ f(b) , и обе производные f’(x) и f’’(x) сохраняют знак во всем промежутке [a; b].
Т.к. действительными корнями уравнения f(x)=0 являются абсциссы точек пересечения кривой y=f(x) с осью ОХ , то отделение корня можно произвести графически.
Иногда полезно уравнение f(x)=0 записать в виде . Действительными корнями исходного уравнения служат абсциссы точек пересечения графиков функций .
Мы рассмотрим 4 численных решения уравнений.
1. Метод дихотомии (метод деления отрезка пополам).
Этот метод можно использовать когда нам предположительно или точно известны границы отрезка, содержащего корень и на этих границах f(x) принимает значения разных знаков, тогда по теореме о достаточных условиях существования корня на заданном отрезке существует хотя бы один корень.
y
- Делим отрезок [a; b] пополам.
- Определяем, на границах какой из частей первоначального интервала функция f(x) меняет знак.
- Полученный интервал снова делим на две части и т.д.
Такой процесс продолжаем до тех пор, пока не перестанут изменяться сохраняемые в ответе десятичные знаки.
Пусть требуется вычислить действительный корень уравнения f(x)=0 , изолированный на отрезке [a;b]. Рассмотрим график функции у= f(x) . Пусть f(а) и f(в) >0. Точки графика А[a;f(a)] и В[b;f(b)] соединим хордой .За приближенное значение искомого корня примем абсциссу х 1 точки пересечения хорды АВ с осью Ох .
Это приближенное значение находится по формуле , где x 1 ∈ (a;b)
Пусть, например, f(x 1 ) тогда за новой (более узкий) промежуток изоляции корня принять [x 1 ,b].
Соединив точки А 1 [x 1 ;f(x 1 )] и В[b;f(b)] , получим в точке пересечения хорды с осью Ох второе приближение x 2 , которое вычислим по формуле: и т.д.
Последовательность чисел a 1 , x 1 , x 2 ,… стремится к искомому корню уравнения f(x)=0 .Вычисление приближенных значений корней уравнения следует вести до тех пор, пока не перестанут изменятся те десятичные знаки, которые мы хотим сохранить в ответе (т.е.пока не будет достигнута заданная степень точности)
Если Х-точный корень уравнения f(x)=0 , изолированный на отрезке [а,в] , а ξ- приближенное значение корня ,найденное методом хорд ,то оценка погрешности этого приближенного значения такова:
- Метод касательных (Метод Ньютона)
Пусть действительный корень уравнения f(x)=0 изолирован на отрезке [а,в] . Будем предполагать, что все ограничения, сформулированные выше относительно f(x) , сохраняют силу и в этом случае. Выделяем на отрезке [а,в] такое число x 0 , при котором f(x 0 ) имеет тот же знак, что и f’’(x 0 ) т.е. f(x 0 ) f’’(x 0 )>0 (в частности , за x 0 может быть принят тот из концов отрезка [а,в] , в котором соблюдено это условие). Проведем в точке Мо[x 0 , f(x 0 )] касательную к кривой y=f(x) .
y= f(x)
За приближенное значение корня примем абсциссу точки пересечения этой касательной с осью Ох . Это приближенное значение корня находится по формуле: .
Применив этот прием вторично в точке M 1 [x 1 ; f(x 1 )] , найдем и т.д.
Полученная т.об. последовательность x 0 , x 1 , x 2 ,… имеет своим пределом искомый корень.
Для оценки погрешности приближенного значения корня, найденного, методом Ньютона, может быть .использовано неравенство:
4. Метод итераций.
Если данное уравнение приведено к виду , где всюду на отрезке [а,в] , на котором исходное уравнение имеет единственный корень, то исходя из некоторого начального .значения x 0 , принадлежащего отрезку [а,в] , можно построить такую последовательность: …
Пределом этой последовательности является единственный корень уравнения f(x)=0 на отрезке [а,в]. Погрешность приближенного значения x n корня Х , найденного методом итерации, оценивается неравенством.
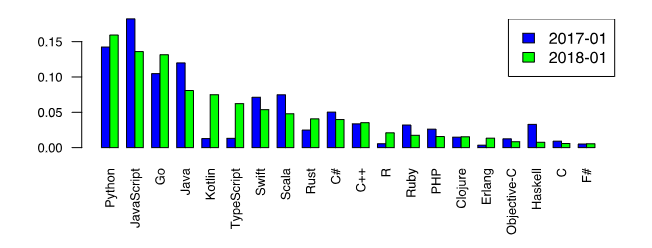
y y=x Численные методы решения систем нелинейных уравненийВведениеМногие прикладные задачи приводят к необходимости нахождения общего решения системы нелинейных уравнений. Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы. Следует отметить интересный факт о том, что любая система уравнений над действительными числами может быть представлена одним равносильным уравнением, если взять все уравнения в форме Для численного решения применяются итерационные методы последовательных приближений (простой итерации) и метод Ньютона в различных модификациях. Итерационные процессы естественным образом обобщаются на случай системы нелинейных уравнений вида: Обозначим через Теперь вернёмся к всеми любимому Python и отметим его первенство среди языков программирования, которые хотят изучать [1]. Этот факт является дополнительным стимулом рассмотрения числительных методов именно на Python. Однако, среди любителей Python бытует мнение, что специальные библиотечные функции, такие как scipy.optimize.root, spsolve_trianular, newton_krylov, являются самым лучшим выбором для решения задач численными методами. С этим трудно не согласится хотя бы потому, что в том числе и разнообразие модулей подняло Python на вершину популярности. Однако, существуют случаи, когда даже при поверхностном рассмотрении использование прямых известных методов без применения специальных функций библиотеки SciPy тоже дают неплохие результаты. Иными словами, новое- это хорошо забытое старое. Так, в публикации [2], на основании проведенных вычислительных экспериментов, доказано, что библиотечная функция newton_krylov, предназначенная для решения больших систем нелинейных уравнений, имеет в два раза меньшее быстродействие, чем алгоритм TSLS+WD Целью настоящей публикации является сравнение по числу итераций, быстродействию, а главное, по результату решения модельной задачи в виде системы из ста нелинейных алгебраических уравнений при помощи библиотечной функции scipy.optimize.root и методом Ньютона, реализованного средствами библиотеки NumPy. Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравненийБиблиотечная функция scipy.optimize.root выбрана в качестве базы сравнения, потому что имеет обширную библиотеку методов, пригодных для сравнительного анализа. scipy.optimize.root(fun, x0, args=(), method=’hybr’, jac=None, tol=None,callback=None, ptions=None) method: Методы решения систем нелинейных уравненийПриведенный далее материал действительно можно прочитать в литературе, например в [4], но я уважаю своего читателя и для его удобства приведу вывод метода по возможности в сокращенном виде. Те, кто не любит формулы, этот раздел пропускают. В методе Ньютона новое приближение для решения системы уравнений (2) определяется из решения системы линейных уравнений: Определим матрицу Якоби: Запишем(3) в виде: Многие одношаговые методы для приближенного решения (2) по аналогии с двухслойными итерационными методами для решения систем линейных алгебраических уравнений можно записать в виде: где При использовании записи (6) метод Ньютона (5) соответствует выбору: Система линейных уравнений (5) для нахождения нового приближения При решении систем нелинейных уравнений можно использовать прямые аналоги стандартных итерационных методов, которые применяются для решения систем линейных уравнений. Нелинейный метод Зейделя применительно к решению (2) дает: В этом случае каждую компоненту нового приближения из решения нелинейного уравнения, можно получить на основе метода простой итерации и метода Ньютона в различных модификациях. Тем самым снова приходим к двухступенчатому итерационному методу, в котором внешние итерации проводятся в соответствии с методом Зейделя, а внутренние — с методом Ньютона. Основные вычислительные сложности применения метода Ньютона для приближенного решения систем нелинейных уравнений связаны с необходимостью решения линейной системы уравнений с матрицей Якоби на каждой итерации, причем от итерации к итерации эта матрица меняется. В модифицированном методе Ньютона матрица Якоби обращается только один раз: Выбор модельной функцииТакой выбор не является простой задачей, поскольку при увеличении числа уравнений в системе в соответствии с ростом числа переменных результат решения не должен меняться, поскольку в противном случае невозможно отследить правильность решения системы уравнений при сравнении двух методов. Привожу следующее решение для модельной функции: Функция f создаёт систему из n нелинейных уравнений, решение которой не зависит от числа уравнений и для каждой из n переменных равно единице. Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корнейТолько один из методов, приведенных в документации [3] прошёл тестирование по результату решения модельной функции, это метод ‘krylov’. Решение для n=100: Solution: Вывод: С увеличением числа уравнений вдвое заметно появление ошибок в решении. При дальнейшем увеличении n решение становится не приемлемым, что возможно из-за автоматической адаптации к шагу, эта же причина резкого падения быстродействия. Но это только моё предположение. Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу НьютонаРешение для n=100: Solution: Решение для n=200: Solution: Чтобы убедиться в том, что программа действительно решает систему, перепишем модельную функцию для ухода от корня со значением 1 в виде: Получим: Вывод: Программа работает и при изменении модельной функции. Теперь вернёмся к начальной модельной функции и проверим более широкий диапазон для n, например в 2 и 500. источники: http://nsportal.ru/npo-spo/estestvennye-nauki/library/2019/05/07/lektsiya-chislennye-metody-resheniya-uravneniy http://habr.com/ru/post/419453/ |

 , возвести их в квадрат и сложить.
, возвести их в квадрат и сложить.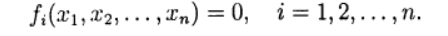 (1)
(1)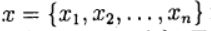 вектор неизвестных и определим вектор-функцию
вектор неизвестных и определим вектор-функцию 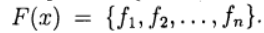 Тогда система (1) записывается в виде уравнения:
Тогда система (1) записывается в виде уравнения: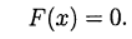 (2)
(2)
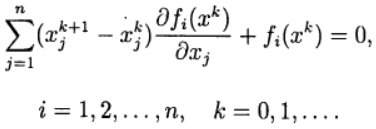 (3)
(3)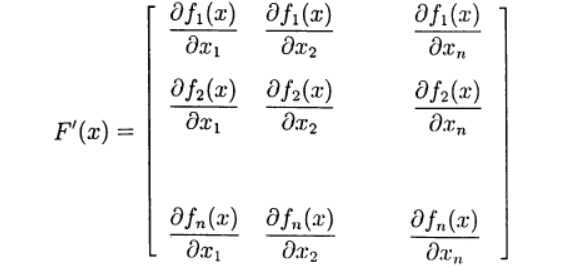 (4)
(4) (5)
(5) (6)
(6)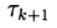 — итерационные параметры, a
— итерационные параметры, a 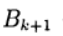 — квадратная матрица n х n, имеющая обратную.
— квадратная матрица n х n, имеющая обратную.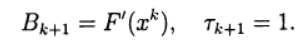
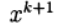 может решаться итерационно. В этом случае мы имеем двухступенчатый итерационный процесс с внешними и внутренними итерациями. Например, внешний итерационный процесс может осуществляться по методу Ньютона, а внутренние итерации — на основе итерационного метода Зейделя
может решаться итерационно. В этом случае мы имеем двухступенчатый итерационный процесс с внешними и внутренними итерациями. Например, внешний итерационный процесс может осуществляться по методу Ньютона, а внутренние итерации — на основе итерационного метода Зейделя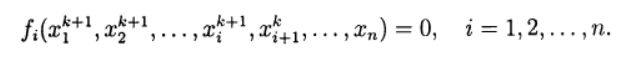 (7)
(7)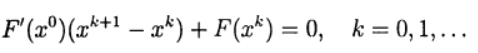 (8)
(8)