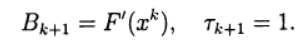Численные методы решения уравнений и решения задач

Численные методы решения краевых задач

Постановка задачи и основные положения

Рассмотрим двухточечные краевые задачи, часто встречающиеся в приложениях, например, при решении задач вариационного исчисления, оптимального управления, механики жидкости и газа и др. Пусть дано обыкновенное дифференциальное уравнение

и краевые условия

где [math]F \bigl(x,y,y’,\ldots,y^<(n)>\bigr);

j=\overline[/math] — функции указанных аргументов, заданные в некоторой области их изменения; [math]L[/math] и [math](n-L)[/math] — число условий на левом и правом концах отрезка [math][a,b][/math] соответственно. Общее количество условий равно порядку дифференциального уравнения. Требуется найти функцию [math]y=y(x)[/math] , которая на отрезке [math][a,b][/math] удовлетворяет уравнению (7.1), а на концах отрезка — краевым условиям (7.2).

Если уравнения (7.1),(7.2) линейны относительно искомой функции и ее производных, то краевая задача называется линейной.

Для простоты ограничимся частным случаем линейной краевой задачи для дифференциального уравнения второго порядка [math](n=2)[/math] , которая наиболее часто ставится в вычислительной практике и записывается в виде

(\Omega \equiv [a,b]),[/math]

где [math]p(x),\, q(x),\, f(x)\in C_2[a,b][/math] — заданные функции, а [math]\alpha_0,\,\alpha_1,\, \beta_0,\, \beta_1,\,A,\,B[/math] — заданные числа, 0,

j=0;1[/math] . Требуется найти функцию [math]y(x)[/math] , удовлетворяющую уравнению (7.3) и краевым условиям (7.4). Краевые условия при [math]\alpha_\ne0,

j=0;1[/math] , задают линейную связь между значениями искомого решения и его производной на концах отрезка [math][a,b][/math] .

В простейшем случае, когда [math]\beta_0=0,

\beta_1=0[/math] , краевые условия задают на концах отрезка [math][a,b][/math] только значения функции [math]y(a),\,y(b)[/math] . Такие функциональные условия называют краевыми условиями первого рода. В этом случае краевая задача называется первой краевой задачей.

В случае, когда [math]\alpha_0=0,

\alpha_1=0[/math] , т.е. на концах отрезка заданы только значения производных, краевые условия являются дифференциальными. Такие краевые условия называют условиями второго рода или «мягкими». Последнее название обусловлено тем, что они определяют на концах отрезка [math][a,b][/math] всего лишь наклоны интегральных кривых, а не значения функции [math]y(x)[/math] . В этом случае задача (7.3),(7.4) называется второй краевой задачей.

В общем случае, когда [math]\alpha_0[/math] и (или) [math]\alpha_1;

\beta_0[/math] и (или) [math]\beta_1[/math] не равны нулю, краевые условия носят функционально-дифференциальный характер и называются условиями третьего рода. Тогда задача (7.3),(7.4) называется третьей краевой задачей.

Например, условия [math]y(a)=A,

y(b)=B[/math] являются условиями первого рода. Геометрически это означает, что при решении первой краевой задачи требуется найти интегральную кривую уравнения (7.3), проходящую через данные точки [math](a,A),\, (b,B)[/math] (рис. 7.1,а). Условия [math]y'(a)=A,\, y'(b)=B[/math] являются условиями второго рода. Геометрически вторая краевая задача сводится к отысканию интегральной кривой уравнения, пересекающей прямые [math]x=a,

x=b[/math] под заданными углами [math]\alpha,\,\beta[/math] , где [math]\operatorname\alpha=A,

\operatorname\beta=B[/math] (рис. 7.1,6). Условия [math]y'(a)=A,

y(b)=B[/math] являются частным случаем краевых условий третьего рода, так как [math]\alpha_0=0,

\beta_1=0[/math] . Геометрически данная краевая задача сводится к отысканию интегральной кривой уравнения, проходящей через точку [math](b,B)[/math] и пересекающей прямую [math]x=a[/math] под данным углом [math]\alpha[/math] , где [math]\operatorname\alpha= A[/math] (рис. 7.1,в).

В общем случае краевая задача может:

а) иметь единственное решение;

б) не иметь решений;

в) иметь несколько или бесконечно много решений.

Утверждение 7.1 (о существовании и единственности решения краевой задачи (7.3),(7.4)). Для того чтобы существовало единственное решение краевой задачи (7.3),(7.4), необходимо и достаточно, чтобы однородная краевая задача

имела только тривиальное решение [math]y(x)\equiv0[/math] .

Пример 7.1. Найти аналитическое решение следующих краевых задач:

0 \leqslant x \leqslant \frac<\pi><2>,

y\! \left(\frac<\pi><2>\right)-y’\! \left(\frac<\pi><2>\right)=2[/math] (третья краевая задача);

0 \leqslant x \leqslant 1,

y(1)=0[/math] (первая краевая задача).

Воспользуемся известной методикой отыскания общих решений дифференциальных уравнений. Подставив в них заданные краевые условия, получим аналитические решения данных краевых задач.

1. Найдем общее решение однородного уравнения [math]y»+y=0[/math] , одинакового для обеих рассматриваемых задач. Так как характеристическое уравнение [math]\lambda^2+1=0[/math] имеет комплексные сопряженные корни [math]\lambda_<1,2>=\pm i= \alpha\pm \beta i[/math] [math](\alpha=0,

\beta=1)[/math] , то общее решение будет

2. Частные решения неоднородных уравнений находятся методом подбора. Подставляя [math]y_<\text>(x)=C[/math] в уравнение [math]y»+y=1[/math] , а [math]y_<\text>(x)=Dx[/math] в уравнение [math]y»+y=-x[/math] , получаем [math]C=1,

D=-1[/math] . Поэтому [math]y_<\text>(x)=1[/math] в случае «а», [math]y_<\text>(x)=-x[/math] в случае «б».

3. Найдем общее решение неоднородного уравнения как сумму общего решения однородного уравнения и частного решения неоднородного уравнения:

а) [math]y(x)=C_1\cos x+C_2\sin x+1[/math] ; б) [math]y(x)=C_1\cos x+C_2\sin x-x[/math] .

4. Определим значения произвольных постоянных из краевых условий третьего рода (случай «а») и первого рода (случай «б»):

а) найдем [math]y'(x)=-C_1\sin x+C_2\cos x[/math] . Тогда

Отсюда [math]C_1=1[/math] и [math]y(x)=1+\cos x[/math] — решение краевой задачи «а»;

б) общее решение [math]y(x)=C_1\cos x+C_2\sin x-x[/math] и, следовательно, [math]y(0)=C_1=0,

y(1)=C_1\cos1+ C_2\sin1-1=0[/math] , отсюда [math]C_2= \frac<1><\sin1>[/math] и [math]y(x)=\frac<\sin x><\sin1>-x[/math] — решение краевой задачи «б». Таким образом, решение краевой задачи представляет собой такое частное решение, которое удовлетворяет краевым условиям.

Рассмотренный метод нахождения аналитического решения краевых задач применим для ограниченного класса задач. Поэтому в вычислительной практике используются численные и приближенно-аналитические методы, позволяющие найти приближенное решение краевых задач, точные аналитические решения которых не могут быть найдены.

Метод сеток

Рассмотрим линейную краевую задачу с краевыми условиями первого рода (первую краевую задачу):

где [math]p(x),q(x),f(x)\in C_2[a,b][/math] — заданные функции; [math]A,\,B[/math] — заданные числа.

Очевидно, любой отрезок [math][a,b][/math] , на котором ищется решение краевой задачи, можно привести к отрезку [math][0;1][/math] с помощью линейного преобразования [math]\widetilde= \frac[/math] . Действительно, тогда новая переменная [math]\widetilde\in [0;1][/math] . В результате без ограничения общности краевая задача (7.5) может быть решена сначала на отрезке [math][0;1][/math] , а затем это решение с помощью преобразования [math]x=a+(b-a)\cdot \widetilde[/math] может быть записано на отрезке [math][a,b][/math] . То же относится и к исследованию свойств полученного решения.

Утверждение 7.2 (о единственности решения краевой задачи (7.5)). Если функции [math]p(x),q(x),f(x)[/math] принадлежат классу [math]C_2[a,b],

q(x) \geqslant 0[/math] на [math][0;1][/math] , то краевая задача (7.5) имеет единственное решение [math]y(x)\in C_4[0;1][/math] .

Для решения задачи (7.5) применим метод сеток, получаемый путем аппроксимации первой и второй производных. Введем равномерную сетку (где [math]n[/math] — число отрезков разбиения)

Функции [math]p(x),q(x),f(x)[/math] заменяются их проекциями на сетку [math]\Omega_n[/math] , то есть [math]p(x)\to p(x_)=p_i,[/math] [math]q(x)\to q(x_)=q_i,[/math] [math]f(x)\to f(x_)= f_i,[/math] . Вместо точного решения [math]y(x)[/math] отыскивается некоторое приближение [math]\widehat_= \widehat(x_)\approx y(x_),

i=\overline<0,n>[/math] . Первая и вторая производные аппроксимируются на трехточечном шаблоне [math](x_,x_,x_)[/math] по формулам второго порядка (5.10),(5.14):

Краевые условия для этой задачи аппроксимируются точно, т.е. [math]y(a)[/math] и [math]y(b)[/math] заменяются на [math]\widehat_<0>[/math] и [math]\widehat_[/math] . После замены от дифференциальной задачи (7.5) переходим к разностной схеме:

представляющей собой систему алгебраических уравнений трехдиагонального вида:

\delta_=f_[/math] . Здесь система (7.6) записана для внутренних узлов сетки [math]\Omega_n[/math] . Она является трехдиагональной системой линейных алгебраических уравнений и решается методом прогонки.

1. Изложенный метод сеток допускает обобщение. Например, его можно применять для решения нелинейной краевой задачи:

где [math]F(x,y)[/math] — нелинейная по [math]y[/math] функция (в общем случае, который здесь не рассматривается, функция [math]F[/math] зависит также и от [math]y'[/math] ).

Рассуждая аналогично рассмотренному выше способу, перейдем к разностной задаче:

В силу нелинейности правой части полученная алгебраическая система является нелинейной и для ее решения нельзя использовать метод прогонки в том виде, в каком он изложен для линейной задачи. Поэтому для ее решения используем метод простых итераций, с помощью которого при фиксированном [math]k[/math] (номер итерации) система алгебраических уравнений (7.8) превращается в линейную, так как величины, входящие в правую часть системы, известны из предыдущей итерации. Действительно, для k-й итерации получается система (которая решается на каждой итерации методом прогонки)

Можно показать, что итерации сходятся при выполнении условия [math]q=\frac<1><8>(x_n-x_0)^2M_1 [math]M_1=\max_<[a,b]>\left|\frac<\partial F><\partial y>\right|[/math] с линейной скоростью.

2. Краевые условия второго и третьего рода в задаче, аналогичной (7.5), могут быть аппроксимированы несколькими способами.

Первый способ. Использование аппроксимационных формул (5.4) первого порядка

В силу первого порядка этих аппроксимаций метод сеток в этом случае также будет иметь первый порядок аппроксимации.

Второй способ. Применение формулы Тейлора и ее преобразование с использованием дифференциального уравнения. Таким способом может быть достигнут второй порядок аппроксимации.

Третий способ. Применение левосторонней (5.8) и правосторонней (5.9) формул, аппроксимирующих производные со вторым порядком:

3. Порядок аппроксимации схемы определяется минимальным порядком аппроксимации дифференциального уравнения и краевых условий.

Алгоритм применения метода сеток

1. Задать сетку [math]\Omega_n[/math] на отрезке [math][a,b][/math] или сформировать ее из условий достижения требуемой точности.

2. Используя аппроксимационные формулы (5.10),(5.14) и один из трех способов аппроксимации краевых условий (в случае, если они второго или третьего рода), перейти от исходной дифференциальной задачи к системе алгебраических уравнений (разностной схеме), неизвестными в которой являются величины, «близкие» к решению краевой задачи в узлах сетки.

3. Найти решение разностной задачи путем решения трехдиагональной системы уравнений и таким образом определить приближенное решение краевой задачи.

Пример 7.2. Найти приближенное решение краевой задачи [math]y»+y=1,

0 \leqslant x \leqslant \frac<\pi><2>,[/math] [math]y'(0)=0,[/math] [math]y\! \left(\frac<\pi><2>\right)-y’\! \left(\frac<\pi><2>\right)=2[/math] при [math]n=3[/math] , используя первый способ аппроксимации краевых условий. Записать разностные схемы для второго и третьего способов при произвольном [math]n[/math] .

В поставленной задаче

Для решения задачи воспользуемся методикой.

1. Так как [math]n=3[/math] , то сетка имеет вид [math]\Omega_3=\[/math] , где [math]x_=ih,

y\! \left(\frac<\pi><6>\right)=y_1,[/math] [math]y\! \left(\frac<\pi><3>\right)=y_2,[/math] [math]y\! \left(\frac<\pi><2>\right)=y_3[/math] . Будем искать приближенные значения [math]\widehat_0,\widehat_1, \widehat_2, \widehat_3[/math] . Проекции функций [math]p(x), q(x), f(x)[/math] на сетку имеют вид [math]p_=0,

2. Составим разностную схему. Согласно (7.6), для внутренних узлов сетки получаем

i=1;2[/math] или [math]\widehat_-(2-h^2)\widehat_+ \widehat_=h^2,

Применим первый способ аппроксимации краевых условий. По формуле (5.4) с учетом условия [math]y'(0)=0[/math] на левом конце имеем

На правом конце [math]y\! \left(\frac<\pi><2>\right)=y_3,

y’\! \left(\frac<\pi><2>\right)=y’_3[/math] , и по второй из формул (7.9) [math]\widehat\,’_<3>= \frac<\widehat_<3>-\widehat_<2>>[/math] . Тогда краевое условие [math]y\! \left(\frac<\pi><2>\right)-y’\! \left(\frac<\pi><2>\right)=2[/math] аппроксимируется выражением

В результате получаем разностную схему первого порядка аппроксимации (трехдиагональную систему линейных алгебраических уравнений)

Сравнивая первое уравнение этой системы с рекуррентным соотношением [math]\widehat_= P_\cdot \widehat_+ Q_[/math] метода прогонки, характеризующим обратный ход, получаем [math]P_0=1,

После этого вычисляются все последующие прогоночные коэффициенты по формулам:

Здесь [math]\alpha_,\beta_,\gamma_[/math] соответствуют коэффициентам левой части полученной алгебраической системы, а [math]\delta_[/math] — правой части.

Далее выполняется обратный ход: [math]\widehat_<3>=Q_3,

\widehat_<2>= P_2\widehat_<3>+ Q_2,

\widehat_<1>= P_1\widehat_<2>+ Q_1[/math] .

Результаты решения краевой задачи приведены в табл. 7.1, в которой последний столбец соответствует точному решению [math]y(x)=1+\cos x[/math] , найденному в примере 7.1.

7.1>>\\\hline i& \alpha_& \beta_& \gamma_& \delta_& P_& Q_& \widehat_& y(x) \\\hline 0& 0&-1,\!0000&-1& 0,\!00000& 1,\!00000& 0& 1,\!8648& 2,\!0000\\\hline 1& 1& 1,\!72584& 1& 0,\!27415& 1,\!37771&-0,\!37770& 1,\!8648& 1,\!8666\\\hline 2& 1& 1,\!72584& 1& 0,\!27415& 2,\!87240&-1,\!87242& 1,\!6277& 1,\!5000\\\hline 3& 1& 0,\!47640&-& 1,\!04200&-& 1,\!21853& 1,\!21853& 1,\!0000\\\hline \end[/math]

В силу того, что краевые условия аппроксимированы с первым порядком относительно [math]h[/math] , в данном случае получена разностная схема первого порядка, так как порядок аппроксимации схемы определяется минимальным порядком аппроксимации дифференциального уравнения и краевых условий.

Воспользуемся вторым способом аппроксимации краевых условий для построения разностной схемы второго порядка аппроксимации. Разложим [math]y(x)[/math] в точке [math]x=x_1[/math] относительно точки [math]x_0[/math] по формуле Тейлора:

Выразим из этого соотношения [math]y'(x_0)[/math] и подставим в него вместо [math]y»(x_0)[/math] выражение [math]y»(x_0)=1-y(x_0)=1-y_0[/math] , определяемое исходным дифференциальным уравнением:

Как показывает это соотношение, дифференциальное условие на левой границе аппроксимируется на двухточечном шаблоне [math](x_0,x_1)[/math] со вторым порядком аппроксимации двухточечным алгебраическим уравнением:

Аналогично получается двухточечное алгебраическое уравнение при / [math]i=n-1[/math] и [math]i=n[/math] . Разложение [math]y(x)[/math] в точке [math]x=x_[/math] относительно точки [math]x_n[/math] по формуле Тейлора имеет вид

Выражая отсюда [math]y'(x_n)[/math] с учетом связи [math]y»(x_n)=1-y(x_n)=1-y_n[/math] , следующей из исходного дифференциального уравнения, получаем

Подставим это выражение в граничное условие:

Таким образом, система линейных алгебраических уравнений в окончательном виде записывается следующим образом:

Эта трехдиагональная система, отличающаяся от полученной первым способом только первым и последним уравнениями, решается численно методом прогонки.

Применим третий способ аппроксимации краевых условий для построения разностной схемы второго порядка. Так, для крайней левой точки используется левосторонняя формула (5.8):

Тогда получается трехточечное алгебраическое уравнение:

Аппроксимация производной [math]y’\! \left(\frac<\pi><2>\right)[/math] в крайней правой точке по правосторонней формуле [math]\widehat\,’_= \frac<1> <2h>\bigl(\widehat_-4\widehat_+ 3\widehat_\bigr)[/math] приводит к трехточечному алгебраическому уравнению:

Тогда в этом случае получается следующая система линейных алгебраических уравнений:

Здесь [math]\widehat_<2>[/math] в первом уравнении и [math]\widehat_[/math] в последнем нарушают ее трехдиагональный характер. В этом случае система приводится к трехдиагональному виду путем исключения [math]\widehat_<2>[/math] и [math]\widehat_[/math] из первых двух и последних двух уравнений системы и после этого решается методом прогонки.

Методы минимизации невязки

Описываемые здесь методы относятся к приближенно-аналитическим и могут применяться при решении достаточно широкого класса задач. На основе одного из приближенно-аналитических методов (метода Галеркина) строится метод конечных элементов, излагаемый в разд. 7.5.

Рассмотрим линейную краевую задачу (7.3),(7.4). Ее решение будем искать в виде

где [math]\varphi_0(x), \varphi_1(x), \ldots, \varphi_m(x)[/math] — элементы заданной системы функций; [math]a_1,\ldots,a_m[/math] — неопределенные коэффициенты. Заданная система функций называется базисной, и ее элементы должны удовлетворять условиям:

а) [math]\varphi_(x)\in C_2[a,b],

б) при любом конечном [math]m[/math] функции [math]\varphi_1(x), \ldots, \varphi_m(x)[/math] линейно независимы на отрезке [math][a,b][/math] ;

в) [math]\varphi_0(x)[/math] удовлетворяет краевым условиям (7.4)

г) [math]\varphi_1(x), \ldots, \varphi_m(x)[/math] удовлетворяют условиям

называется невязкой . Она равна разности левой и правой частей уравнения (7.3), образующейся при подстановке [math]\widehat_(x)[/math] вместо [math]y(x)[/math] в дифференциальное уравнение, и характеризует степень отклонения функции [math]\widehat_(x)[/math] от точного решения краевой задачи. Если при некоторых значениях коэффициентов [math]a_1,\ldots,a_m[/math] невязка тождественно равна нулю на отрезке [math][a,b][/math] , а именно

то функция [math]\widehat_(x)[/math] совпадает с точным решением краевой задачи (7.3),(7.4), так как удовлетворяются и уравнение, и краевые условия.

Однако при решении краевых задач, как правило, не удается получить невязку тождественно равной нулю. Поэтому ставится задача: вычислить коэффициенты [math]a_1,\ldots,a_m[/math] таким образом, чтобы невязка в каком-либо смысле стала меньшей. Полученные в результате коэффициенты определяют приближенное решение (7.11).

Выражение для невязки [math]\varepsilon(x; a_1,\ldots, a_m)[/math] с учетом (7.11) удобно записывать в следующей эквивалентной форме:

где [math]L\widehat_\equiv \widehat\,»_(x)+ p(x)\widehat\,’_(x)-q(x) \widehat_(x),

L[/math] — линейный оператор задачи (7.3),(7.4) (выполняются равенства [math]L(y+z)= Ly+Lz,[/math] [math]L(Cy)=C\cdot Ly[/math] для любых [math]y,\,z[/math] и постоянной [math]C[/math] ).

Рассмотрим различные методы, минимизирующие невязку .

А. Метод коллокации. На интервале [math](a,b)[/math] задаются т точек [math]x_1,\ldots, x_n[/math] (точек коллокации) и требуется, чтобы в каждой из них невязка (7.14) обращалась в нуль:

С учетом (7.16) эта система принимает вид

Если полученная система [math]m[/math] линейных уравнений совместна, то из нее определяются коэффициенты [math]a_1,\ldots, a_m[/math] , которые затем подставляются в (7.11).

Б. Метод наименьших квадратов (непрерывный вариант). Неизвестные коэффициенты [math]a_1,\ldots, a_m[/math] должны обеспечивать минимум интеграла от квадрата невязки:

Для решения задачи применяются необходимые условия безусловного экстремум:

Подставляя (7.16) в (7.19), получаем систему [math]m[/math] линейных алгебраических уравнений для нахождения коэффициентов [math]a_1,\ldots, a_m\colon[/math]

В. Метод наименьших квадратов (дискретный вариант). Неизвестные коэффициенты [math]a_1,\ldots,a_m[/math] должны обеспечивать минимум суммы квадратов значений невязки в заданном наборе точек [math]x_1,\ldots,x_n;

n \geqslant m[/math] , то есть [math]x_\in (a,b),

Для решения задачи применяются необходимые условия безусловного экстремума

Отсюда следует система [math]m[/math] линейных уравнений для нахождения коэффициентов [math]a_1,\ldots,a_m[/math] , которая по форме записи совпадает с (7.20), но скалярное произведение определяется по формуле [math]\textstyle<(f,g)= \sum\limits_^ f(x_)g(x_)>[/math] .

Замечание. При [math]n=m[/math] результаты, полученные точечным методом наименьших квадратов и методом коллокации, совпадают. В этом случае точки [math]x_1,\ldots, x_n[/math] являются точками коллокации.

Г. Метод моментов (взвешенных невязок). Неизвестные коэффициенты ах. ат находятся из условия равенства нулю /и моментов невязки:

j=\overline<1,m>[/math] — функции, удовлетворяющие условиям:

б) функции [math]\psi_(x)[/math] являются элементами системы степеней [math]x[/math] или системы тригонометрических функций.

j=\overline<1,m>[/math] называются весовыми, а условие (7.22) является условием ортогональности невязки к весовым функциям.

Д. Метод Галсркина. Он является частным случаем метода моментов, когда в качестве весовых функций используются базисные. Коэффициенты [math]a_1,\ldots,a_m[/math] находятся из условия ортогональности функций базисной системы [math]\varphi_1(x),\ldots, \varphi_(x)[/math] к невязке:

Отсюда следует система [math]m[/math] линейных уравнений для нахождения коэффициентов:

Известно, что при достаточно большом [math]m[/math] условие (7.23) обеспечивает малость невязки в среднем.

Алгоритм применения методов минимизации невязки

1. В выражении (7.11) выбрать систему базисных функций, задать число [math]m[/math] в зависимости от требуемой точности.

2. Найти коэффициенты [math]a_1,\ldots,a_m[/math] путем решения одной из систем алгебраических уравнений (7.18),(7.20),(7.24) в зависимости от выбранного метода.

3. Выписать приближенное решение краевой задачи по формуле (7.11).

Пример 7.3. Найти приближенное решение краевой задачи [math]y»+y=-x,

0 \leqslant x \leqslant 1,[/math] [math]y(0)=0,

y(1)=0[/math] методом коллокации, интегральным методом наименьших квадратов, методом Галеркина

В поставленной задаче

Точное решение найдено в примере 7.1.

Воспользуемся сначала методом коллокации.

1. Зададим [math]m=2[/math] и будем искать решение в виде

где [math]\varphi_0(x)\equiv0[/math] (эта функция удовлетворяет каждому из краевых условий, т.е. [math]\varphi_0(0)=0,

\varphi_0(1)=0[/math] ), функции [math]\varphi_1(x)= x(1-x),

\varphi_2(x)= x^2(1-x)[/math] . Функции [math]\varphi_1(x),\, \varphi_2(x)[/math] линейно независимые, дважды непрерывно дифференцируемые и удовлетворяют условию (7.13). Действительно,

Таким образом, решение краевой задачи ищется в форме

2. Так как [math]m=2[/math] и [math]\varphi_0(x)\equiv 0[/math] , то система (7.18) имеет вид

Выберем узлы коллокации: [math]x_1=1\!\!\not<\phantom<|>>\,4,

Таким образом, имеем линейную систему относительно [math]a_1[/math] и [math]a_2\colon[/math]

3. Приближенное решение задачи: [math]\widehat_2(x)= \frac<217>(42+40x)[/math] .

Решим теперь задачу методом наименьших квадратов (см. непрерывный вариант).

1. Решение краевой задачи ищется в форме [math]\widehat_2(x)= a_1\cdot x(1-x)+ a_2\cdot x^2(1-x)[/math] .

2. Так как [math]f(x)=-x,

\varphi_0(x)\equiv 0[/math] , то система (7.20) имеет вид

Итак, имеем линейную систему относительно [math]a_1[/math] и [math]a_2\colon[/math]

Приближенное решение задачи: [math]\widehat_2(x)=0,\!1875419x(1-x)+ 0,\!1694707x^2(1-x).[/math] .

Решим задачу методом Галеркина.

1. Пусть сначала [math]m=1[/math] . Решение ищется в форме [math]\widehat_1(x)= a_1\cdot x(1-x)[/math] .

2. Тогда система (7.24) преобразуется к виду

Так как [math]\varphi_1(x)= x(1-x),

L\varphi_1(x)= \varphi»_1(x)+ \varphi_1(x)=-2+x(1-x)[/math] , получаем

После вычисления интегралов имеем уравнение [math]-\frac<3><10>\,a_1=-\frac<1><12>[/math] , откуда [math]a_1=\frac<5><18>[/math] .

3. Приближенное решение краевой задачи: [math]\widehat_1(x)=\frac<5><18>\,x(1-x)[/math] . Пусть теперь [math]m=2[/math] .

1. Решение краевой задачи ищется в форме [math]\widehat_2(x)=a_1\cdot x(1-x)+ a_2\cdot x^2(1-x)[/math] .

2. Тогда система (7.24) имеет вид

Вычисляя интегралы, находим

3. Приближенное решение краевой задачи: [math]\widehat_2(x)= x(1-x)\! \left(\frac<71><369>+ \frac<7><41>\,x\right)[/math] .

Сопоставим полученные решения с точным (табл. 7.2).

7.2>>\\\hline x& y_<\text>& y_<\text>& y_<\text>& \text \\\hline 0,\!25& 0,\!045& 0,\!04311& 0,\!0440& 0,\!044014 \\\hline 0,\!50& 0,\!071& 0,\!06807& 0,\!0698& 0,\!069747 \\\hline 0,\!75& 0,\!062& 0,\!05899& 0,\!0600& 0,\!060050 \\\hline \end[/math]

Очевидно, метод Галеркина дал более точный результат.

Пример 7.4. Найти приближенное решение краевой задачи [math]y»+2xy’-2y=2x^2,

0 \leqslant x \leqslant 1,[/math] [math]y'(0)=-2,

y(1)+y'(1)=0[/math] методом Галеркина.

В поставленной задаче

1. Зададим [math]m=2[/math] и подберем функции [math]\varphi_0(x),\, \varphi_1(x),\, \varphi_2(x)[/math] , используя систему [math]1,x,x^2,\ldots[/math] . Функция [math]\varphi_0(x)[/math] должна удовлетворять условиям (7.12):

Пусть [math]\varphi_0(x)=b+cx[/math] , где [math]b,\,c[/math] — неопределенные коэффициенты. Тогда

Отсюда [math]b=4[/math] и [math]\varphi_0(x)=4-2x[/math] .

Функции [math]\varphi_1(x),\, \varphi_2(x)[/math] должны удовлетворять условиям (7.13):

Первое условие выполняется для функций вида [math]\varphi_= x^+b_[/math] . Значения [math]b_[/math] находятся из второго условия [math]1+b_+j+1=0[/math] , откуда [math]b_=-j-2[/math] . Тогда получаем [math]\varphi_1(x)=x^2-3,

Таким образом, решение краевой задачи ищется в форме

2. Тогда система (7.24) имеет вид

3. Приближенное решение краевой задачи [math]\widehat_2(x)= x^2-2x+1[/math] .

Методы сведения краевой задачи к задаче Коши

Метод стрельбы. Суть этого метода заключается в сведении решения краевой задачи к многократному решению задачи Коши. Принцип построения метода стрельбы рассмотрим на примере нелинейной краевой задачи:

где [math]f(x,y,y’)[/math] — нелинейная функция, обусловливающая нелинейность дифференциального уравнения (7.25).

При введении новой переменой [math]z=y'[/math] уравнение (7.25) записывается в нормальной форме Коши, а краевые условия видоизменяются:

где [math]\eta=y'(a)=\operatorname\alpha[/math] — параметр, равный тангенсу угла наклона интегральной кривой в точке [math]x=a[/math] . Угол [math]\alpha[/math] (параметр [math]\eta[/math] ) в процессе многократного решения краевой задачи должен принять такое значение, чтобы интегральная кривая «попала в цель», т.е. в точку [math](b,B)[/math] (рис.7.2 ,а). В общем случае полученное при некотором значении [math]\eta[/math] решение [math]y(x,\eta)[/math] не будет удовлетворять условию [math]y(b,\eta)=B[/math] на правом конце отрезка.

Следовательно, требуется найти такое значение параметра [math]\eta[/math] , чтобы оно было корнем нелинейного уравнения [math]\Phi(\eta)= y(b,n)-B=0[/math] . Для решения этого уравнения, как правило, используются методы половинного деления или секущих. В случае использования метода половинного деления сначала делают «пробные» выстрелы при выбранных наугад или в соответствии с некоторым алгоритмом значениях [math]\eta[/math] до тех пор, пока среди значений [math]\Phi(\eta)[/math] не окажется двух противоположных по знаку. Им соответствует начальный интервал неопределенности, который далее последовательно сокращается путем деления пополам. При применении метода секущих используется формула

где [math]\eta^<(0)>,\,\eta^<(1)>[/math] — начальные значения параметра, [math]k[/math] — номер итерации. Итерации прекращаются при выполнении условия окончания [math]\bigl|\Phi(\eta^<(k)>)\bigr| \leqslant \varepsilon[/math] или [math]\bigl|\eta^<(k+1)>-\eta^<(k)>\bigr| \leqslant \varepsilon[/math] с некоторым положительным [math]\varepsilon[/math] , характеризующим точность решения задачи.

Замечание. Точность решения краевой задачи зависит не только от точности определения параметра [math]\eta[/math] , но также и от точности решения соответствующей задачи Коши. Поэтому одновременно с уточнением параметра [math]\eta[/math] рекомендуется уменьшать шаг при решении задачи Коши, либо выбирать более точный метод.

Рассмотрим применение метода стрельбы для решения линейной краевой задачи (7.3),(7.4):

Численные методы решения в алгебре и геометрии

Современная вычислительная техника требует от пользователей знаний основ вычислительной математики и применения этих знаний к решению различных задач народного хозяйства. Сложные вычислительные задачи, включающие при моделировании различных процессов и явлений можно разбить на ряд элементарных: решение уравнений, установление функциональной зависимости между результатами эксперимента, вычисление интегралов и т.д.. При решении очень многих практических задач математическая модель выражается уравнением. В школьном курсе математики мы рассматривали линейные, квадратные уравнения, уравнения третьей и четвертой степени, при решении этих уравнений получали целые, дробные и рациональные решения.

При подготовке к итоговой аттестации в одном из сборников мне встретилось уравнение х 3 +2х -7=0, которое я не смогла решить, применяя способы рассматриваемые в школьной программе. Преподователь сказал, что такое уравнение имеет приближенные корни.

А как решить уравнение, если корни его выражаются приближенными числами? На этот вопрос мне удалось найти ответ, только после изучения темы «Производная».

Скачать:

Вложение	Размер
исследовательская работа по алгебре и теории чисел	362 КБ

Предварительный просмотр:

Муниципальное образовательное учериждение

Кировская средняя общеобразовательная школа

Исследовательская работа по математике

«Численные методы решения

в алгебре и геометрии.»

Выполнила: ученица 11 класса

МОУ Кировская СОШ

Руководитель: учитель математики

МОУ Кировская СОШ

п. Средний Маныч

I. Историческая справка.

II. Численные методы решения уравнений.

1. Традиционный способ определения корней уравнения.

3. Метод косательной (метод Ньютона).

4. Комбинированный метод хорд и касательных.

5. Метод (метод последовательных приближений).

6. Метод проб (метод половинного деления).

III. Решение задач.

IV. Численные методы в геометрии.

Цель работы: научиться находить приблизительные корни уравнений n-ной степени и трансцендентных уравнений.

При решении уравнений f(x) = 0 вначале графически находим интервал изоляции, в котором находится корень уравнения. Затем, после такого отделения корней, каждый из них может быть вычислен с любой степенью точности посредством аналитических методов. В работе рассматривается метод хорд, метод касательных (метод Ньютона), метод итераций(метод последовательных приближений) и метод проб (половиного деления).

С помощью описанных методов можно решать задачи практического содержания в различных отраслях народного хозяйства: бухгалтерии, ветеринарии, медицине, промышленности и т.д. – там, где поставленна любая математическая модель задач, сводящаяся к алгебраическим уравнениям.

I. Историческая справка.

Представьте, что в очень легком – практически невесомом – кошельке содержится какое-то количество монет одинакового достоинства. Как узнать, сколько монет в кошельке, не заглядывая внутрь? Есть очень простой способ: положить кошелек на одну чашу рычажных весов и уравновесить его монетками на другой чаше. Сколько монет для этого потребуется – столько же их и в кошельке.

Испытанный измерительный инструмент продавцов, химиков и аптекарей приходит на помощь и в чуть более сложном случае: пусть на левой чаше находящихся в равновесии весов лежат кошелек с неизвестным числом монет и еще 5 монет рядом с ним, а на правой чаше – 15 точно таких же монеток. Для того чтобы узнать, сколько монет в кошельке, снимем по 5 монет с обеих чаш – равновесие при этом не нарушится. Следовательно, внутри кошелька 10 монет.

В те далекие времена, когда мудрецы впервые стали задумываться о равенствах, содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. «Ищется куча, которая вместе с двумя третями ее, половиной и одной седьмой составляет 37. », – поучал во II тысячелетии до новой эры египетский писец Ахмес. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущуства. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.

Дошедшие до нас источники свидетельствуют, что древние ученные владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описание этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: «Смотри!», «Делай так!», «Ты правильно нашел». В этом смысле исключением является «Арифметика» греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений.

Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово «аль-джебр» из арабского названия этого тракта – «Китаб аль-джебр валь-мукабала» («Книга о восстановлении и противопоставлении») – со временем превратилось в хорошо знакомое всем слово «алгебра», а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.

Большой вклад в теорию о решении уравнений внес итальянский ученный Леонардо Пизанский.

Среди современников ему не было равных. И в последующие три столетия нельзя назвать ни одного ученного такого масштаба. Творчество Леонардо Пизанского (1180 – 1240) оказало решающее влияние на развитие алгебры и теории чисел, в частности на исследования таких математиков, как Франсуа Виет и Пьер Ферма.

При дворе Фридриха II устраивались научные диспуты. На одном из них придворный философ магистр Иоганн Палермский предложил Леонардо пизанскому два вопроса, которые в современных обозначениях выглядят так:

1) найти корень уравнения

х 3 + 2х 2 + 10х = 20;

2) найти рациональные решения системы уравнений

х 2 +5= и 2 ,

Леонардо провел тщательные исследования обеих хадач и написал две книги – «Цветок» и «Книга квадратов» (или «Книга о квадратных числах») 1225.), посвященные их решению. Хотя обе работы изданы типографическим способом только в 1862 г., математикам средневековой Европы они были хорошо известны.

В первой книге Леонардо установил, что корень уравнения (1) не является ни целым числом, ни дробью. Он также не может иметь вид n, n + m или n – m. Наконец, Леонардо вычислил его с точностью до шестого шестидесятеричного знака:

х = 1; 22, 7, 42, 33, 4, 40

(здесь точка с запятой отделяют целую часть от дробной, а запятые – шестидесятиричные разряды). Каким способом было полученно это значение, до сих пор остается неизвестным.

Если квадратные уравнения умели решать еще математики Вавилонии и Древней Индии, то решение урувненийпри n > 3 появились немного в конце XV века. А вот применение численных методов при нахождении корней уравнений впервые встречаются в работах Исаака Ньютона.

II. Численные методы решения алгебраических уравнений

Пусть требуется решить алгебраическое уравнение

Методы исследования поведения функции дают возможность находить приближенные значения корней уравнения (1.1).

Если данное уравнение есть алгебраическое уравнение, т.е. f ‘(х) есть многочлен, первой, второй, третьей или четвертой степени, то существуют формулы, позволяющие выразить корни уравнения через его коэффициенты с помощью конечного числа операций сложения, вычитания, умножения, деления и извлечения корней. Для уравнения выше четвертой таких формул, вообще говоря, нет.

Если коэффициенты любого уравнения, алгебраического или неалгебраического (трансцендентного), не буквенные, а числовые, то корни уравнения могут быть вычислены приближенно с любой степенью точности. Отметим, что даже в тех случаях, когда корни алгебраического уравнения выражаются через радикалы, на практике иногда целесообразно применять приближенный метод решения уравнения.

i. 1 .Графический метод, отделение корней

Задача о нахождении приближенных значений действительных корней уравнения (1.1) предусматривает предварительное отделение корня, т.е. установление промежутка, в котором других корней данного уравнения нет.

Будем предполагать, что функция f(х) в промежутке [а; b ] непрерывна со своими производными f'(х) и f «(х), значения f (а) и f (b) функции на концах промежутка имеют разные знаки, т.е. f(а) •f(b) /»(х) сохраняют знак во всем промежутке [а’,b].

Действительные корни уравнения (1.1) являются абсциссами точек пересечения кривой у =f(х) с осью Ох, а если это уравнение преобразуется к виду f 1 (х) = f 2 (х), то его действительные корни будут абсциссами точек пересечения кривых у f,(х) и у = f г (х) (см. рис.).

Численные методы решения систем нелинейных уравнений

Введение

Многие прикладные задачи приводят к необходимости нахождения общего решения системы нелинейных уравнений. Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.

Следует отметить интересный факт о том, что любая система уравнений над действительными числами может быть представлена одним равносильным уравнением, если взять все уравнения в форме , возвести их в квадрат и сложить.

Для численного решения применяются итерационные методы последовательных приближений (простой итерации) и метод Ньютона в различных модификациях. Итерационные процессы естественным образом обобщаются на случай системы нелинейных уравнений вида:

(1)

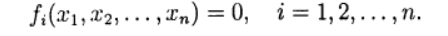
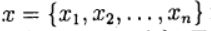
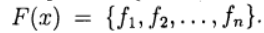
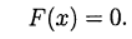
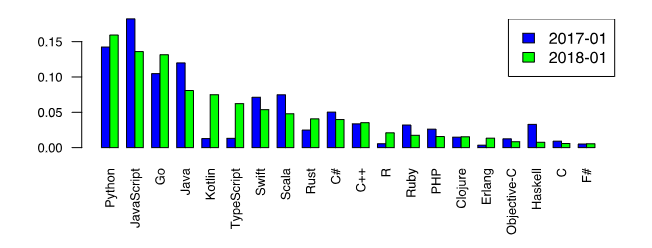
Обозначим через вектор неизвестных и определим вектор-функцию Тогда система (1) записывается в виде уравнения:

(2)

Теперь вернёмся к всеми любимому Python и отметим его первенство среди языков программирования, которые хотят изучать [1].

Этот факт является дополнительным стимулом рассмотрения числительных методов именно на Python. Однако, среди любителей Python бытует мнение, что специальные библиотечные функции, такие как scipy.optimize.root, spsolve_trianular, newton_krylov, являются самым лучшим выбором для решения задач численными методами.

С этим трудно не согласится хотя бы потому, что в том числе и разнообразие модулей подняло Python на вершину популярности. Однако, существуют случаи, когда даже при поверхностном рассмотрении использование прямых известных методов без применения специальных функций библиотеки SciPy тоже дают неплохие результаты. Иными словами, новое- это хорошо забытое старое.

Так, в публикации [2], на основании проведенных вычислительных экспериментов, доказано, что библиотечная функция newton_krylov, предназначенная для решения больших систем нелинейных уравнений, имеет в два раза меньшее быстродействие, чем алгоритм TSLS+WD
(two-step least squares), реализованный средствами библиотеки NumPy.

Целью настоящей публикации является сравнение по числу итераций, быстродействию, а главное, по результату решения модельной задачи в виде системы из ста нелинейных алгебраических уравнений при помощи библиотечной функции scipy.optimize.root и методом Ньютона, реализованного средствами библиотеки NumPy.

Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений

Библиотечная функция scipy.optimize.root выбрана в качестве базы сравнения, потому что имеет обширную библиотеку методов, пригодных для сравнительного анализа.

scipy.optimize.root(fun, x0, args=(), method=’hybr’, jac=None, tol=None,callback=None, ptions=None)
fun — Векторная функция для поиска корня.
x0 –Начальные условия поиска корней

method:
hybr -используется модификация Пауэлл гибридный метод;
lm – решает системы нелинейных уравнений методом наименьших квадратов.
Как следует из документации [3] методы broyden1, broyden2, anderson, linearmixing, diagbroyden, excitingmixing, krylov являются точными методами Ньютона. Остальные параметры являются «не обязательными» и с ними можно ознакомится в документации.

Методы решения систем нелинейных уравнений

Приведенный далее материал действительно можно прочитать в литературе, например в [4], но я уважаю своего читателя и для его удобства приведу вывод метода по возможности в сокращенном виде. Те, кто не любит формулы, этот раздел пропускают.

В методе Ньютона новое приближение для решения системы уравнений (2) определяется из решения системы линейных уравнений:

(3)

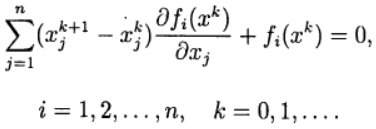
Определим матрицу Якоби:

(4)

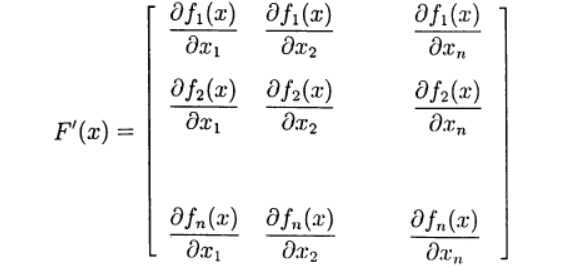
Запишем(3) в виде:

(5)

Многие одношаговые методы для приближенного решения (2) по аналогии с двухслойными итерационными методами для решения систем линейных алгебраических уравнений можно записать в виде:

(6)

где — итерационные параметры, a — квадратная матрица n х n, имеющая обратную.

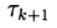
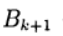
При использовании записи (6) метод Ньютона (5) соответствует выбору:

Система линейных уравнений (5) для нахождения нового приближения 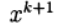может решаться итерационно. В этом случае мы имеем двухступенчатый итерационный процесс с внешними и внутренними итерациями. Например, внешний итерационный процесс может осуществляться по методу Ньютона, а внутренние итерации — на основе итерационного метода Зейделя

При решении систем нелинейных уравнений можно использовать прямые аналоги стандартных итерационных методов, которые применяются для решения систем линейных уравнений. Нелинейный метод Зейделя применительно к решению (2) дает:

(7)

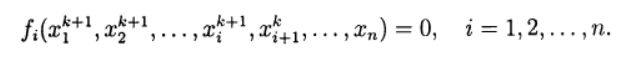
В этом случае каждую компоненту нового приближения из решения нелинейного уравнения, можно получить на основе метода простой итерации и метода Ньютона в различных модификациях. Тем самым снова приходим к двухступенчатому итерационному методу, в котором внешние итерации проводятся в соответствии с методом Зейделя, а внутренние — с методом Ньютона.

Основные вычислительные сложности применения метода Ньютона для приближенного решения систем нелинейных уравнений связаны с необходимостью решения линейной системы уравнений с матрицей Якоби на каждой итерации, причем от итерации к итерации эта матрица меняется. В модифицированном методе Ньютона матрица Якоби обращается только один раз:

(8)

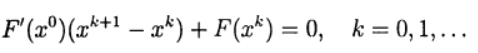
Выбор модельной функции

Такой выбор не является простой задачей, поскольку при увеличении числа уравнений в системе в соответствии с ростом числа переменных результат решения не должен меняться, поскольку в противном случае невозможно отследить правильность решения системы уравнений при сравнении двух методов. Привожу следующее решение для модельной функции:

Функция f создаёт систему из n нелинейных уравнений, решение которой не зависит от числа уравнений и для каждой из n переменных равно единице.

Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней

Только один из методов, приведенных в документации [3] прошёл тестирование по результату решения модельной функции, это метод ‘krylov’.

Решение для n=100:

Вывод: С увеличением числа уравнений вдвое заметно появление ошибок в решении. При дальнейшем увеличении n решение становится не приемлемым, что возможно из-за автоматической адаптации к шагу, эта же причина резкого падения быстродействия. Но это только моё предположение.

Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона

Решение для n=100:

Решение для n=200:

Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1.]
Newton iteration = 14
Newton method time 1.869 seconds

Чтобы убедиться в том, что программа действительно решает систему, перепишем модельную функцию для ухода от корня со значением 1 в виде:

Получим:
Solution:
[ 0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1.31649896 0.6865098 0.89609091 0.98509235]
Newton iteration = 16
Newton method time 0.046 seconds

Вывод: Программа работает и при изменении модельной функции.

Теперь вернёмся к начальной модельной функции и проверим более широкий диапазон для n, например в 2 и 500.
n=2
Solution:
[1. 1.]
Newton iteration = 6
Newton method time 0.048 seconds
n=500

источники:

http://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2014/02/09/chislennye-metody-resheniya-v-algebre-i-geometrii

http://habr.com/ru/post/419453/