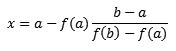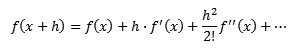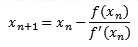Численные методы решения уравнений паскаль

Численные методы решения уравнений паскаль

Nickolay.info. Обучение. Библиотека численных методов на Паскале

Материал публикуется в связи с сессией, так как многие не просто изучают численные методы, но еще и программируют их на старом добром Паскале 🙂 В помощь таким страждущим студентам — наша старая добрая (конца XX века) бибилиотека численных методов на Паскале.

Сами численные методы реализованы в библиотеке LPM2.TPU (исходник в соответствующем файле .PAS), все остальные файлы с расширением .PAS — демки для вызовов разных функций библиотеки. Паскаль версии 7.1 можно взять на этой странице сайта.

Скиньте все файлы *.pas из архива в удобную папку, а скомпилированную библиотеку lpm2.tpu — в папку, которая указана в настройке Options -> Unit Directories верхнего меню Паскаля. Затем открывайте и запускайте нужные программы.

Вот текущий список модулей для численных методов (в алфавитном порядке):

• EMPIRICH.PAS — эмпирическая зависимость по массивам X,Y переменной размерности (*).
• FPRM.PAS — определённый интеграл методом средних прямоугольников. Задаются пределы интегрирования a,b, число узловых точек n, в коде определяется функция f(x).
• FSIMP.PAS — определённый интеграл методом Симпсона. Данные задаются, как для модуля FPRM, плюс требуемая точность.
• FTRAP.PAS — определённый интеграл методом трапеций. Данные задаются, как для модуля FPRM.
• INTER.PAS — реализация первой и второй интерполяционной формулы Ньютона. вводятся размер таблицы, массивы значений X и Y, значение аргумента для интерполяционной формулы и номер формулы (1 или 2).
• KLGRAPH.PAS — графопостроитель по данным массивов X,Y. Задаются целочисленные ширина и высота сетки (по сути дела, они обозначают размеры картинки в пикселах), количество горизонтальных и вертикальных осей (ячеек сетки), размер таблицы, затем массивы данных X и Y (могут быть вещественными).
• MITER.PAS — метод итераций решения уравнения. Функция уравнения задана программно как F(X)=D1*x*x*x+D2*x*x+D3*x+D4, вводятся коэффийиенты D1,D2,D3,D4, начальное приближение для x, константа метода и желаемая точность вычисления.
• MNEWTON.PAS — метод Ньютона для решения уравнения. Данные вводятся как для MITER (кроме константы метода).
• ODY1.PAS — обыкновенное дифференциальное уравнение 1 порядка, методы Эйлера (обычный и модифицированный), Рунге-Кутта. Вводятся интервал [a,b], шаг разностной сетки, начальное условие. Функция задается подпрограммой F(X,y). (*).
• ODY2.PAS — обыкновенное дифференциальное уравнение 2 порядка. Вводятся коэффициенты уравнения P,G,F, коэффициенты 1-го и 2-го краевых условий, интервал [a,b], шаг разностной сетки. Функции программируются подпрограммами P1(x), G1(x), F1(x) (*).
• ODY22.PAS — модификация ODY2, не имеет самостоятельного значения (*).
• OPT.PAS — методы оптимизации. Поиск экстремумов унимодальных функций одной переменной. Функция задается подпрограммой F(x). Реализованы методы равномерного поиска, поразрядного приближения, дихотомии (половинного деления), золотого сечения. (*)
• PROG.PAS — решение системы линейных алгебраических уравнений (СЛАУ) методом прогонки. Вводятся порядок системы, матрица коэффициентов системы, вектор свободных членов.
• TGRAPH.PAS — построение графика функции, заданной подпрограммой F(X). Вводятся ширина и высота сетки (по сути дела, размеры картинки графика в пикселах), число горизонтальных и вертикальных осей (линий сетки), интервал построения графика. (*)
• ZEID.PAS — решение системы линейных алгебраических уравнений (СЛАУ) методом Зейделя. Вводятся порядок системы, матрица коэффициентов системы, вектор свободных членов, точность вычисления, максимальное число итераций.

Здесь (*) означает, что предполагается переход в графический режим для вывода картинки.

Если Ваш компьютер — такой новый, что уже не показывает DOS-графику, поставьте DOSBox и DOSShell (ссылка есть внизу этой страницы сайта). Тогда Вы сможете скомпилировать в Паскале исполняемый файл (включив в Паскале настройку верхнего меню Compile -> Destination в значение Disk) и потом запустить его из DOSBox или DOSShell.

Решение нелинейных уравнений на языке программирования Pascal

Практически перед каждым программистом рано или поздно встает задача определения корней уравнения. На сегодняшний день существует достаточно много алгоритмов решения данной задачи. Из этой статьи вы узнаете о наиболее известных алгоритмах численного решения уравнений. Практически все они могут быть разделены на два этапа: отделения и уточнения корней. Первую часть легко выполнить графическим методом. Для выполнения второго этапа решения уравнения можно воспользоваться одним из многих методов уточнения корней уравнения.

Наиболее простым в реализации является метод бисекции, или как его еще называют, метод половинного деления. Это итерационный метод, суть которого заключается в том, что на каждой итерации интервал сокращается вдвое до тех пор, пока не будет найдено решение с заданной точностью.

Данный метод достаточно прост и содержит всего два действия. Сначала находится переменная х – середина интервала [a,b]. После чего вычисляется значение функции в середине интервала. Затем определяется, совпадает ли по знаку значение функции в середине интервала, со знаком функции в левой части. В случаи если их знаки равны, то новой левой границей считается середина интервала, в ином же случаи правой граница интервала считается его середина. Таким образом, при каждой итерации интервал сокращается вдовое то справа, то слева. Очень часто можно встретить следующую реализацию данного метода.

Этот вариант, хотя и очень прост для понимания, содержит один недостаток. Дело в том, что если функция очень сильно изменяется, то при заданной точности, её значение может очень сильно отличаться. Поэтому для исключения этой неточности выгоднее использовать цикл с постусловием и сравнивать с заданным значением точности не разницу границ интервала, а значение функции. Тогда реализация метода примет следующий вид.

Другим очень хорошим методом нахождения корней уравнения, который несколько сложнее в реализации, чем предыдущий, является метод хорд. Отличается он тем, что границы интервала соединяются прямой линией, то есть хордой. Затем определяется точка пересечения этой прямой с осью абсцисс, по формуле:

После чего находится значение функции в точке пересечения. По аналогии с предыдущим методом определяется новая левая или правая граница интервала, которой является точка пересечения. Реализация данного метода на языке программирования Pascal может быть представлена следующим образом.

Еще одним хорошим методом решения уравнений является метод касательных или метод Ньютона. Главное его отличие от представленных ранее методов биссекции и хорд – отсутствие необходимости отделения корня. Вместо этого нужно задать лишь начальное приближение. Однако его главным недостатком остается сложность реализации, связанная, прежде всего с необходимостью определять производные исходного уравнения.

В основе метода Ньютона лежит разложения функции в ряд Тейлора:

Обычно значения ряда, содержащие шаг h во второй и более высоких степенях отбрасывают, так как их влияние на результат незначительны.

Суть метода заключается в экстраполяции функции касательными. После того как пользователь задает начальное приближение, программа должна определить точку пересечения касательной к графику функции с осью абсцисс. Для этого используется формула:

Затем находится значение функции в точке пересечения касательной с осью абсцисс и если получившиеся значение близко к нулю, то считается, что решение уравнения найдено. Реализация данного метода может быть представлена следующим образом

К сожалению, при всех своих достоинствах метод Ньютона не гарантирует сходимости. Отсутствия решения может возникнуть по нескольким причинам. Например, это может произойти из-за того, что касательная будет параллельна оси абсцисс. В этом случаи необходимо предусмотреть выход из цикла при достижении большого количества итераций.

Существуют также и другие методы, например, золотого сечения. Какой из них использовать решать вам, однако следует отметить, что наиболее быстродейственным считается метод Ньютона, затем метод хорд и последним по быстродействию является метод половинного деления. Хотя количество итераций напрямую зависит от введенных начальных данных. При удачном стечении обстоятельств решение каждым из методов может быть найдено даже при единственной итерации.

Численные методы (язык Паскаль) © К.Ю. Поляков, 2008-2009 1.Решение уравненийРешение уравнений 2.Вычисление площади (интеграла)Вычисление площади (интеграла) — презентация

Презентация была опубликована 8 лет назад пользователемmail.g177.ru

Похожие презентации

Презентация на тему: » Численные методы (язык Паскаль) © К.Ю. Поляков, 2008-2009 1.Решение уравненийРешение уравнений 2.Вычисление площади (интеграла)Вычисление площади (интеграла)» — Транскрипт:

1 Численные методы (язык Паскаль) © К.Ю. Поляков, Решение уравненийРешение уравнений 2.Вычисление площади (интеграла)Вычисление площади (интеграла) 3.Вычисление длины кривойВычисление длины кривой 4.ОптимизацияОптимизация

2 Численные методы (язык Паскаль) Тема 1. Решение уравнений © К.Ю. Поляков,

3 3 Основные понятия Типы решения: аналитическое (точное, в виде формулы) приближенное (неточное) Задача: решить уравнение Как? ? численные методы начальное приближение при N графический метод

4 4 Численные методы Идея: последовательное уточнение решения с помощью некоторого алгоритма. Область применения: когда найти точное решение невозможно или крайне сложно. 1)можно найти хоть какое-то решение 2)во многих случаях можно оценить ошибку (то есть можно найти решение с заданной точностью) 1)нельзя найти точное решение 2)невозможно исследовать решение при изменении параметров 3)большой объем вычислений 4)иногда сложно оценить ошибку 5)нет универсальных методов

5 5 Есть ли решение на [a, b] ? x y x*x* a b x y x*x* a b есть решение нет решения x y x*x* a b Если непрерывная функция f (x) имеет разные знаки на концах интервала [a, b], то в некоторой точке x * внутри [a, b] имеем f (x * ) = 0 ! !

6 6 Метод дихотомии (деление пополам) 1.Найти середину отрезка [a,b] : c = (a + b) / 2; 2.Если f(c)*f(a)

7 7 Метод дихотомии (деления пополам) простота можно получить решение с заданной точностью (в пределах точности машинных вычислений) нужно знать интервал [a, b] на интервале [a, b] должно быть только одно решение большое число шагов для достижения высокой точности только для функций одной переменной

eps do begin c := (a + b) / 2; if f(a)*f(c) eps do begin c := (a + b) / 2; if f(a)*f(c) 9 9 Как подсчитать число шагов? function BinSolve (a, b, eps: real; var N: integer ): real; var c:real; begin N := 0; while b — a > eps do begin c := (a + b) / 2; if f(a)*f(c) eps do begin c := (a + b) / 2; if f(a)*f(c) eps do begin c := (a + b) / 2; if f(a)*f(c) eps do begin c := (a + b) / 2; if f(a)*f(c) eps do begin c := (a + b) / 2; if f(a)*f(c) eps do begin c := (a + b) / 2; if f(a)*f(c) eps do begin c := (a + b) / 2; if f(a)*f(c)

10 10 Метод итераций (повторений) Задача: Эквивалентные преобразования: имеет те же решения при Идея решения: – начальное приближение (например, с графика) Проблемы: 1)как лучше выбрать ? 2)всегда ли так можно найти решение?

11 11 Сходимость итераций Сходящийся итерационный процесс: последовательность приближается (сходится) к точному решению. односторонняя сходимость двусторонняя сходимость

12 12 Расходимость итераций Расходящийся итерационный процесс: последовательность неограниченно возрастает или убывает, не приближается к решению. односторонняя расходимость двусторонняя расходимость

13 13 От чего зависит сходимость? сходится расходится Выводы: сходимость итераций зависит от производной итерации сходятся при и расходятся при сходимость определяется выбором параметра b

14 14 Как выбрать b ? наугад, пробовать разные варианты для начального приближения x 0 пересчитывать на каждом шаге, например: Какие могут быть проблемы? ?

16 16 Метод Ньютона (метод касательных) Какая связь с методом итераций? ?

17 17 Метод Ньютона (программа) < Newton решение уравнения методом Ньютона Вход: x – начальное приближение eps - точность решения Выход: решение уравнения f(x)=0, n - число шагов >function Newton (x, eps: real; var N: integer): real; var dx: real; OK: boolean; begin N := 0; OK := False; while not OK and (N

18 18 Метод Ньютона быстрая (квадратичная) сходимость – ошибка на k -ом шаге обратно пропорциональна k 2 не нужно знать интервал, только начальное приближение применим для функция нескольких переменных нужно уметь вычислять производную (по формуле или численно) производная не должна быть равна нулю может зацикливаться

19 Численные методы (язык Паскаль) Тема 2. Вычисление площади (интеграла) © К.Ю. Поляков,

20 20 Площадь криволинейной трапеции x y b a y = f (x) x y b a y = f 1 (x) y = f 2 (x)

21 function Area(x1, x2:real): real; var x, S, h: real; begin S := 0; h := 0.001; x := x1; while x

22 22 Метод (правых) прямоугольников x y x2x2 x1x1 h y = f 1 (x) y = f 2 (x) S1S1S1S1 S2S2S2S2 S3S3S3S3 S4S4S4S4 SiSiSiSi x x+h f 1 (x) f 2 (x) function Area(x1, x2:real): real; var x, S, h: real; begin S := 0; h := 0.001; x := x1; while x

23 function Area(x1, x2:real): real; var x, S, h: real; begin S := 0; h := 0.001; x := x1; while x

25 25 Метод Монте-Карло Применение: вычисление площадей сложных фигур (трудно применить другие методы). Требования: необходимо уметь достаточно просто определять, попала ли точка (x, y) внутрь фигуры. Пример: заданы 100 кругов (координаты центра, радиусы), которые могу пересекаться. Найти площадь области, перекрытой кругами. Как найти S ? ?

26 26 Метод Монте-Карло 1.Вписываем сложную фигуру в другую фигуру, для которой легко вычислить площадь (прямоугольник, круг, …). 2.Равномерно N точек со случайными координатами внутри прямоугольника. 3.Подсчитываем количество точек, попавших на фигуру: M. 4. Вычисляем площадь: Всего N точек На фигуре M точек 1.Метод приближенный. 2.Распределение должно быть равномерным. 3.Чем больше точек, тем точнее. 4.Точность ограничена датчиком случайных чисел. !

27 Численные методы (язык Паскаль) Тема 3. Вычисление длины кривой © К.Ю. Поляков,

28 28 Длина кривой x y b a y = f (x) L Точное решение: нужна формула для производной сложно взять интеграл Приближенное решение: xixi x i +h f (x)f (x) LiLi L1L1 L2L2 LNLN

30 Численные методы Тема 4. Оптимизация © К.Ю. Поляков,

31 31 Найти x, при котором или при заданных ограничениях. Основные понятия Оптимизация – поиск оптимального (наилучшего в некотором смысле) решения. Цель: определить значения неизвестных параметров, при которых заданная функция достигает минимума (затраты) или максимума (доходы). Ограничения – условия, которые делают задачу осмысленной. или

32 32 Локальные и глобальные минимумы y = f (x) глобальный минимум локальные минимумы Задача: найти глобальный минимум. Реальность: большинство известных алгоритмов находят только локальный минимум вблизи начальной точки алгоритмы поиска глобального минимума в общем случае неизвестны Что делать: для функций одной переменной начальная точка определяется по графику случайный выбор начальной точки запуск алгоритма поиска с нескольких разных точек и выбор наилучшего результата

33 33 Минимум функции одной переменной Дано: на интервале [a,b] функция непрерывна и имеет единственный минимум. Найти: x * y = f (x) Принцип сжатия интервала: Как выбрать c и d наилучшим образом? ?

34 34 Минимум функции одной переменной Постоянное сжатие в обоих случаях: y = f (x) Коэффициент сжатия: Самое быстрое сжатие: при должно быть c d Метод «почти половинного» деления: – малое число нужно искать два значения функции на каждом шаге

35 35 Отношение «золотого сечения» Идея: выбрать c и d так, чтобы на каждом шаге вычислять только одно новое значение функции. Уравнение для определения g : Отношение «золотого сечения»:

36 36 Метод «золотого сечения» < Gold поиск минимума функции («золотое сечение») Вход: a, b – границы интервала, eps – точность Выход: x, при котором f(x) имеет минимум на [a,b] >function Gold(a, b, eps:real): real; const g = ; var x1, x2, R: real; begin R := g*(b — a); while abs(b-a) > eps do begin x1 := b — R; x2 := a + R; if f(x1) > f(x2) then a := x1 else b := x2; R := R * g; end; Gold := (a + b) / 2; end; < Gold поиск минимума функции («золотое сечение») Вход: a, b – границы интервала, eps – точность Выход: x, при котором f(x) имеет минимум на [a,b] >function Gold(a, b, eps:real): real; const g = ; var x1, x2, R: real; begin R := g*(b — a); while abs(b-a) > eps do begin x1 := b — R; x2 := a + R; if f(x1) > f(x2) then a := x1 else b := x2; R := R * g; end; Gold := (a + b) / 2; end; Как вычислять только одно значение на каждом шаге? ? eps do begin x1 := b — R; x2 := a + R; if f(x1) > f(x2) then a := x1 else b := x2; R := R * g; end; Gold := (a + b) / 2; end; <---------------------------------------------- Gold поиск минимума функции («золотое сечение») Вход: a, b – границы интервала, eps – точность Выход: x, при котором f(x) имеет минимум на [a,b] ---------------------------------------------->function Gold(a, b, eps:real): real; const g = 0.618034; var x1, x2, R: real; begin R := g*(b — a); while abs(b-a) > eps do begin x1 := b — R; x2 := a + R; if f(x1) > f(x2) then a := x1 else b := x2; R := R * g; end; Gold := (a + b) / 2; end; Как вычислять только одно значение на каждом шаге? ?»>

37 37 Функции нескольких переменных Найти, для которых при заданных ограничениях. Проблемы: нет универсальных алгоритмов поиска глобального минимума неясно, как выбрать начальное приближение (зависит от задачи и интуиции) Подходы: методы локальной оптимизации (результат зависит от выбора начального приближения) случайный поиск (без гарантии) методы глобальной оптимизации (для особых классов функций)

38 38 Метод покоординатного спуска Идея: выбираем начальную точку будем менять только x 1, а остальные переменные «заморозим», находим минимум по x 1 теперь будем менять только x 2, а остальные переменные «заморозим», … начальное приближение минимум простота, сводится к нескольким задачам с одной переменной можно двигаться к минимуму быстрее большой объем вычислений может не найти решение для сложных функций

39 39 Градиентные методы Градиент – это вектор, показывающий направление наискорейшего возрастания функции. Идея: выбираем начальную точку на каждом шаге двигаемся в направлении, противоположном градиенту минимум начальное приближение быстрая сходимость необходимо считать производные (по формуле или численно) плохо работает для быстро меняющихся функций градиент

40 40 Метод случайного поиска Идея: выбираем начальную точку пробуем сделать шаг в случайном направлении если значение функции уменьшилось, шаг удачный (запоминается) минимум начальное приближение простота реализации не требует вычисления производных много вариантов с самообучением хорошо работает для функций с многими локальными минимумами очень большой объем вычислений