Численные методы решения уравнений с одним неизвестным

Общие сведения о численном решении уравнений с одним неизвестным

Пусть задана непрерывная функция f(x). Требуется найти корни уравнения f(x) = 0 численными методами – это и является постановкой задачи. Численное решение уравнения распадается на несколько подзадач:

Анализ количества, характера и расположения корней (обычно путем построения графика функции или исходя из физического смысла исследуемой модели). Здесь возможны следующие варианты:
- единственный корень;
- бесконечное множество решений;
- корней нет;
- имеется несколько решений, как действительных, так и мнимых (например, для полинома степени n). Корни четной кратности выявить сложно.
Локализация корней (разбиение на интервалы) и выбор начального приближения к каждому корню. В простейшем случае можно протабулировать функцию с заданным шагом.

Если в двух соседних узлах функция будет иметь разные знаки, то между этими узлами лежит нечетное число корней уравнения (по меньшей мере один).

Метод дихотомии (бисекций)

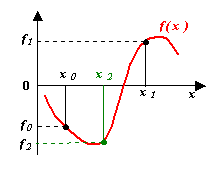
Иначе называется методом половинного деления. Пусть задан начальный интервал [x₀, x₁], на котором f(x₀)f(x₁) ≤ 0 (т.е. внутри имеется не менее чем один корень). Найдем x₂ = ½ (x₀ + x₁) и вычислим f(x₂). Если f(x₀)f(x₂) ≤ 0, используем для дальнейшего деления отрезок [x₀, x₂], если > 0 – используем для дальнейшего деления отрезок [x₁, x₂], и продолжаем деление пополам.

Итерации продолжаются, пока длина отрезка не станет меньше 2ξ – заданной точности. Тогда середина последнего отрезка даст значение корня с требуемой точностью. В качестве иного критерия можно взять
| f(x)| ≤ ξ_y.

Скорость сходимости метода невелика, однако он прост и надежен. Метод неприменим к корням четной кратности. Если на отрезке несколько корней, то заранее неизвестно, к какому из них сойдется процесс.

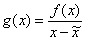
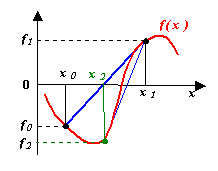
Если на заданном интервале предполагается несколько корней, то существует возможность последовательно исключать найденные корни из рассмотрения. Для этого воспользуемся вспомогательной функцией , где – только что найденный корень. Для функций f(x) и g(x) совпадают все корни, за исключением (в этой точке полюс функции g(x)). Для достижения требуемой точности рекомендуется грубо приблизиться к корню по функции g(x), а затем уточнить его, используя f(x).

Идея метода проиллюстрирована рисунком. Задается интервал [ x₀, x₁], на котором f(x₀)f(x₁) ≤ 0, между точками x₀ и x₁ строится хорда, стягивающая f(x). Очередное приближение берется в точке x₂, где хорда пересекает ось абсцисс. В качестве нового интервала для продолжения итерационного процесса выбирается тот, на концах которого функция имеет разные знаки. Условия выхода из итерационного цикла: 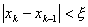или | f(x)| ≤ ξ_y.

Для вывода итерационной формулы процесса найдем точку пересечения хорды (описываемой уравнением прямой) с осью абсцисс: ax₂ + b = 0, где 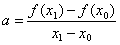; b = f(x₀) — ax₀.

Отсюда легко выразить .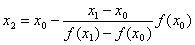

Метод хорд в большинстве случаев работает быстрее, чем метод дихотомии. Недостатки метода те же, что и в предыдущем случае.

Метод Ньютона (касательных.

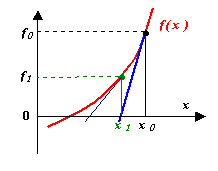
Пусть x₀ – начальное приближение к корню, а f(x) имеет непрерывную производную. Следующее приближение к корню найдем в точке x₁, где касательная к функции f(x), проведенная из точки (x₀, f₀), пересекает ось абсцисс. Затем точно так же обрабатываем точку(x₁, f₁), организуя итерационный процесс. Выход из итерационного процесса по условию .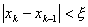

Уравнение касательной, проведенной из точки (x₀, f₀): y(x) = f / (x₀)(x-x₀) + f(x₀) дает для y ( x ₁) = 0 следующее выражение:

, (1)

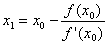
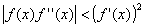
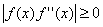
которое и используется для организации итерационного процесса. Итерации сходятся, только если всюду выполняется условие ; в противном случае сходимость будет не при любом начальном приближении, а только в некоторой окрестности корня. Итерации будут сходиться к корню с той стороны, с которой .

Метод обладает самой высокой скоростью сходимости: погрешность очередного приближения примерно равна квадрату погрешности предыдущего приближения. Метод можно использовать для уточнения корней в области комплексных чисел, что необходимо при решении многих прикладных задач, например при численном моделировании электромагнитных колебательных и волновых процессов с учетом временной и пространственной диссипации энергии.

Недостатком метода можно указать необходимость знать явный вид первой и второй производных, так как их численный расчет приведет к уменьшению скорости сходимости метода. Иногда, ради упрощения расчетов, используют т.н. модифицированный метод Ньютона, в котором значениеf / (x) вычисляется только в точке x₀, при этом число итераций увеличивается, но расчеты на каждой итерации упрощаются.

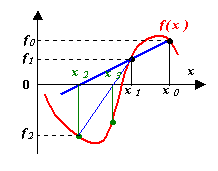
В отличие от метода Ньютона, можно заменить производную первой разделенной разностью, найденной по двум последним итерациям, т.е. заменить касательную секущей. При этом первый шаг итерационного процесса запишется так:

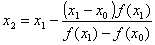
Для начала итерационного процесса необходимо задать x₀ и x₁, которые не обязательно ограничивают интервал, на котором функция должна менять знак; это могут быть любые две точки на кривой. Выход из итерационного процесса по условию .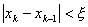

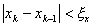
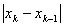
Сходимость может быть немонотонной даже вблизи корня. При этом вблизи корня может происходить потеря точности, т.н. «разболтка решения», особенно значительная в случае кратных корней. От разболтки страхуются приемом Гарвика: выбирают некоторое ξ_x и ведут итерации до выполнения условия . Затем продолжают расчет, пока убывает. Первое же возрастание может свидетельствовать о начале разболтки, а значит, расчет следует прекратить, а последнюю итерацию не использовать.

Метод простых итераций.

Суть метода простых итераций в принципе совпадает с методом, изложенным для решения систем линейных алгебраических уравнений. Для нелинейного уравнения метод основан на переходе от уравнения

К эквивалентному уравнению x = φ(x). Этот переход можно осуществить разными способами, в зависимости от вида f(x). Например, можно положить

где b = const, при этом корни исходного уравнения (2) не изменятся.

Если известно начальное приближение к корню x₀, то новое приближение x₁ = φx(₀), т.е. общая схема итерационного процесса:

Наиболее простой критерий окончания процесса .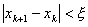

Критерий сходимости метода простых итераций: если вблизи корня |φ / (x)| / (x)| = 0. При этом, исходя из (3), b = –1/f / (x), и итерационная формула (4) переходит в

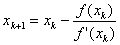
т.е. в формулу метода Ньютона (1). Таким образом, метод Ньютона является частным случаем метода простых итераций, обеспечивающим самую высокую скорость сходимости из всех возможных вариантов выбора функции φ(x).

Численные методы решения систем нелинейных уравнений

Введение

Многие прикладные задачи приводят к необходимости нахождения общего решения системы нелинейных уравнений. Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.

Следует отметить интересный факт о том, что любая система уравнений над действительными числами может быть представлена одним равносильным уравнением, если взять все уравнения в форме , возвести их в квадрат и сложить.

Для численного решения применяются итерационные методы последовательных приближений (простой итерации) и метод Ньютона в различных модификациях. Итерационные процессы естественным образом обобщаются на случай системы нелинейных уравнений вида:

(1)

Обозначим через вектор неизвестных и определим вектор-функцию Тогда система (1) записывается в виде уравнения:

(2)

Теперь вернёмся к всеми любимому Python и отметим его первенство среди языков программирования, которые хотят изучать [1].

Этот факт является дополнительным стимулом рассмотрения числительных методов именно на Python. Однако, среди любителей Python бытует мнение, что специальные библиотечные функции, такие как scipy.optimize.root, spsolve_trianular, newton_krylov, являются самым лучшим выбором для решения задач численными методами.

С этим трудно не согласится хотя бы потому, что в том числе и разнообразие модулей подняло Python на вершину популярности. Однако, существуют случаи, когда даже при поверхностном рассмотрении использование прямых известных методов без применения специальных функций библиотеки SciPy тоже дают неплохие результаты. Иными словами, новое- это хорошо забытое старое.

Так, в публикации [2], на основании проведенных вычислительных экспериментов, доказано, что библиотечная функция newton_krylov, предназначенная для решения больших систем нелинейных уравнений, имеет в два раза меньшее быстродействие, чем алгоритм TSLS+WD
(two-step least squares), реализованный средствами библиотеки NumPy.

Целью настоящей публикации является сравнение по числу итераций, быстродействию, а главное, по результату решения модельной задачи в виде системы из ста нелинейных алгебраических уравнений при помощи библиотечной функции scipy.optimize.root и методом Ньютона, реализованного средствами библиотеки NumPy.

Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений

Библиотечная функция scipy.optimize.root выбрана в качестве базы сравнения, потому что имеет обширную библиотеку методов, пригодных для сравнительного анализа.

scipy.optimize.root(fun, x0, args=(), method=’hybr’, jac=None, tol=None,callback=None, ptions=None)
fun — Векторная функция для поиска корня.
x0 –Начальные условия поиска корней

method:
hybr -используется модификация Пауэлл гибридный метод;
lm – решает системы нелинейных уравнений методом наименьших квадратов.
Как следует из документации [3] методы broyden1, broyden2, anderson, linearmixing, diagbroyden, excitingmixing, krylov являются точными методами Ньютона. Остальные параметры являются «не обязательными» и с ними можно ознакомится в документации.

Методы решения систем нелинейных уравнений

Приведенный далее материал действительно можно прочитать в литературе, например в [4], но я уважаю своего читателя и для его удобства приведу вывод метода по возможности в сокращенном виде. Те, кто не любит формулы, этот раздел пропускают.

В методе Ньютона новое приближение для решения системы уравнений (2) определяется из решения системы линейных уравнений:

(3)

Определим матрицу Якоби:

(4)

Запишем(3) в виде:

(5)

Многие одношаговые методы для приближенного решения (2) по аналогии с двухслойными итерационными методами для решения систем линейных алгебраических уравнений можно записать в виде:

(6)

где — итерационные параметры, a — квадратная матрица n х n, имеющая обратную.

При использовании записи (6) метод Ньютона (5) соответствует выбору:

Система линейных уравнений (5) для нахождения нового приближения может решаться итерационно. В этом случае мы имеем двухступенчатый итерационный процесс с внешними и внутренними итерациями. Например, внешний итерационный процесс может осуществляться по методу Ньютона, а внутренние итерации — на основе итерационного метода Зейделя

При решении систем нелинейных уравнений можно использовать прямые аналоги стандартных итерационных методов, которые применяются для решения систем линейных уравнений. Нелинейный метод Зейделя применительно к решению (2) дает:

(7)

В этом случае каждую компоненту нового приближения из решения нелинейного уравнения, можно получить на основе метода простой итерации и метода Ньютона в различных модификациях. Тем самым снова приходим к двухступенчатому итерационному методу, в котором внешние итерации проводятся в соответствии с методом Зейделя, а внутренние — с методом Ньютона.

Основные вычислительные сложности применения метода Ньютона для приближенного решения систем нелинейных уравнений связаны с необходимостью решения линейной системы уравнений с матрицей Якоби на каждой итерации, причем от итерации к итерации эта матрица меняется. В модифицированном методе Ньютона матрица Якоби обращается только один раз:

(8)

Выбор модельной функции

Такой выбор не является простой задачей, поскольку при увеличении числа уравнений в системе в соответствии с ростом числа переменных результат решения не должен меняться, поскольку в противном случае невозможно отследить правильность решения системы уравнений при сравнении двух методов. Привожу следующее решение для модельной функции:

Функция f создаёт систему из n нелинейных уравнений, решение которой не зависит от числа уравнений и для каждой из n переменных равно единице.

Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней

Только один из методов, приведенных в документации [3] прошёл тестирование по результату решения модельной функции, это метод ‘krylov’.

Решение для n=100:

Вывод: С увеличением числа уравнений вдвое заметно появление ошибок в решении. При дальнейшем увеличении n решение становится не приемлемым, что возможно из-за автоматической адаптации к шагу, эта же причина резкого падения быстродействия. Но это только моё предположение.

Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона

Решение для n=100:

Решение для n=200:

Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1.]
Newton iteration = 14
Newton method time 1.869 seconds

Чтобы убедиться в том, что программа действительно решает систему, перепишем модельную функцию для ухода от корня со значением 1 в виде:

Получим:
Solution:
[ 0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1.31649896 0.6865098 0.89609091 0.98509235]
Newton iteration = 16
Newton method time 0.046 seconds

Вывод: Программа работает и при изменении модельной функции.

Теперь вернёмся к начальной модельной функции и проверим более широкий диапазон для n, например в 2 и 500.
n=2
Solution:
[1. 1.]
Newton iteration = 6
Newton method time 0.048 seconds
n=500

Численные методы решения нелинейного уравнения с одним неизвестным

Вы будете перенаправлены на Автор24

Численные методы решения нелинейного уравнения с одним неизвестным — это методы приближённого определения корня нелинейного уравнения, которое используется в случаях, когда точный метод решения недоступен или весьма трудоёмок.

Введение

Методики решения уравнений могут быть поделены на две группы:

Прямые методы.
Итерационные методы.

Прямые методы применяют законченные выражения, то есть формулы, для вычисления неизвестных. Они позволяют найти решение после осуществления заранее определённого количества операций. Они считаются относительно простыми и самыми универсальными, то есть являются пригодными для решения широкого класса линейных и нелинейных задач.

К недостаткам прямых методов следует отнести:

Необходимо сохранять в оперативной памяти компьютера сразу всю матрицу. При больших размерах матрицы требуется много места в памяти.
Накопление погрешности в процессе решения. Это может быть особенно опасным для больших систем, а также для плохо обусловленных систем, которые чувствительны к погрешностям.

Итерационными методами являются методы последовательных приближений. В этих методах следует задавать определённое приближённое решение, именуемое начальным приближением. Затем при помощи заданного алгоритма выполняется один цикл вычислений, который называется итерацией. Итогом итерации является нахождение нового приближения. Итерации осуществляются до тех пор, пока не будет получено решение с необходимой точностью.

К преимуществам итерационных, то есть численных методов, следует отнести:

Эти методы предполагают хранение в памяти компьютера не всей матрицы системы, а только нескольких векторов с n элементами.
Погрешность окончательного результата при использовании итерационных методик не может накапливаться, поскольку точность вычислений во всех итерациях должна определяться по итогам предыдущей итерации и фактически не зависти от ранее осуществлённых операций.

Готовые работы на аналогичную тему

Численные методы решения нелинейного уравнения с одним неизвестным

Технологическая последовательность вычислительного процесса может состоять из следующих этапов:

Создание математической модели исследуемого объекта. Сюда же необходимо отнести и анализ модели, поверку корректности полученной математической задачи.
Создание алгоритма вычислений, то есть, методики приблизительного решения поставленной задачи.
Формирование программной реализации алгоритма на компьютере и её проверка.
Осуществление серии вычислений при варьировании основных параметров начальной задачи и алгоритма.
Осуществление анализа полученных результатов.

Все перечисленные этапы допускают возможность возврата к любому из предшествующих этапов для его уточнения и изменения. Иногда вычислительные алгоритмы разрешения непростых задач создаются из набора главных компонентов, представляющих собой алгоритмы решения некоторых типичных математических задач. Владение численными методами решения подобных задач считается необходимым условием использования передовых технологий математического моделирования.

Идеология модели лежит в основе того, что называется методами вычислительной математики. Как правило, алгоритм приблизительного решения базируется на том положении, что исходная математическая задача будет заменяться (аппроксимироваться) некоторой более простой задачей или даже совокупностью более простых задач.

Предположим, что существует непрерывная функция f(x) и необходимо определить корни уравнения f(x) = 0 численными методами, что, по сути, будет считаться постановкой задачи. Численное решение уравнения подразделяется на следующий набор подзадач:

Осуществление анализа числа, характера и расположения корней, как правило, путем формирования графика функции или на основе физического смысла исследуемой модели. При этом корень может быть единственным, корней может быть также бесконечное множество или не быть вовсе. Есть также вариант, когда существует несколько решений, как действительных, так и мнимых, к примеру, для полинома степени n. Корни четной кратности достаточно сложно выявить.
Осуществление локализации корней, то есть разбиение на интервалы, и выбор начального приближения к каждому корню. В простейшем случае можно выполнить табуляцию функцию с заданным шагом. Если в двух соседних узлах функция имеет различные знаки, то между этими узлами расположено нечетное количество корней уравнения (по крайней мере один).
Определение каждого (или того, который интересует) корня уравнения с необходимой точностью. Уточнение может осуществляться при помощи разных методов.

Одним из численных методов решения нелинейных уравнений является метод дихотомии (бисекций), который по-другому именуется методом половинного деления. Предположим, что имеется начальный интервал $[x_0, x_1]$, на котором $f(x_0)f(x_1) ≤ 0$, то есть внутри интервала расположен по крайней мере один корень.

График показан на рисунке ниже.

Рисунок 1. График. Автор24 — интернет-биржа студенческих работ

А далее необходимо вычислить $f(x_2)$. В случае, если $f(x_0)f(x_2) ≤ 0$, следует использовать для последующего деления отрезок $[x_0, x_2]$. Если же функция больше нуля, то необходимо использовать для последующего деления отрезок $[x_1, x_2]$, и продолжить деление пополам.

Итерации должны продолжаться до тех пор, пока длина отрезка не станет меньше $2ξ$, то есть меньше необходимой точности. В этом случае середина последнего отрезка даёт величину корня с необходимой точностью. В качестве другого критерия может быть принято следующее условие:

Скорость сходимости данной методики невелика, но она является достаточно простой и надёжной. Этот метод не может быть использован при наличии корней с четной кратностью. Когда на отрезке имеется несколько корней, то заранее нельзя предвидеть, к какому именно корню может сойтись данный процесс.

Когда на исследуемом интервале может быть больше одного корня, то имеется возможность поочерёдного исключения найденных корней из рассмотрения.

источники:

http://habr.com/ru/post/419453/

http://spravochnick.ru/informatika/chislennye_metody_resheniya_nelineynogo_uravneniya_s_odnim_neizvestnym/