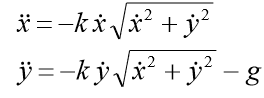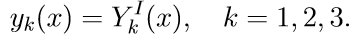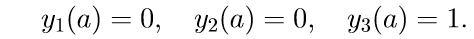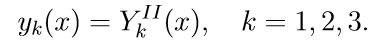Численные решения уравнения функционально дифференциальных уравнение
Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,у’)=0 или у’=f(x,y). Функция y(x), при подстановке которой уравнение обращается в тождество, называется решением дифференциального уравнения.
Рассмотрим несколько численных методов решения дифференциальных уравнений первого порядка. Описание численных методов приводится для уравнения в виде у’=f(x,y).
Рассмотрим два варианта вывода расчетных формул
Численные методы решения эволюционных функционально-дифференциальных уравнений Текст научной статьи по специальности « Математика»
Аннотация научной статьи по математике, автор научной работы — Жуковская Татьяна Владимировна, Молоканова Елена Анатольевна
Рассматривается общий метод приближенного решения задачи Коши для функционально-дифференциального уравнения эволюционного типа. На основании общего метода получены аналоги классических методов Эйлера и Рунге-Кутты для численного решения функционально-дифференциальных уравнений . Приведены условия сходимости методов
Похожие темы научных работ по математике , автор научной работы — Жуковская Татьяна Владимировна, Молоканова Елена Анатольевна
NUMERICAL METHODS FOR SOLUTION OF EVOLUTIONARY FUNCTIONAL-DIFFERENTIAL EQUATIONS
General method for construction of approximate solution to the Cauchy problem for evolutionary functional-differential equation is described. Analogs of the Euler method and the Runge-Kutta method for numerical methods of solution of evolutionary functional-differential equations are given on the basis of this method. Conditions for convergence of methods are presented.
Текст научной работы на тему «Численные методы решения эволюционных функционально-дифференциальных уравнений»
УДК 517.988.6, 519.62
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЭВОЛЮЦИОННЫХ ФУНКЦИОНАЛЬНО-ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
© Т. В. Жуковская, Е. А. Молоканова
Ключевые слова: вольтерров оператор; т -вольтерров оператор; функционально-дифференциальное уравнение; задача Коши; приближенное решение; численные методы. Рассматривается общий метод приближенного решения задачи Коши для функционально-дифференциального уравнения эволюционного типа. На основании общего метода получены аналоги классических методов Эйлера и Рунге-Кутты для численного решения функционально-дифференциальных уравнений. Приведены условия сходимости методов.
Функционально-дифференциальные уравнения описывают многочисленные процессы в физике, технике, экономике, медицине и т. д. Найти «точное» решение таких уравнений можно только в исключительных случаях, поэтому особенно актуальной является задача приближенного решения функционально-дифференциальных уравнений. В работах 1 для линейного уравнения рассматриваются методы приближенного построения функции Коши, основанные на построении обратного оператора и аппроксимации ядра оператора ступенчатыми функциями. Ряд работ посвящен численным методам решений специальных типов функционально-дифференциальных уравнений 6: с авторегулируемым запаздыванием, нейтрального типа, интегро-дифференциальным и др. В случае, когда решение дифференциального уравнения не продолжаемо на весь отрезок [a, b] и имеет вертикальную асимптоту, в [10, 11] предлагается модификация метода Эйлера для численного построения решения.
В настоящей работе предлагается общий подход к построению численных методов решения уравнения
Здесь оператор F : ACp[a,b] ^ Lp[a,b] является вольтерровым [12], т. е.
Vy £ [0,b — a] Vxi, x2 £ ACp[a, b]
(xi(t) = X2(t) Vt £ [a,a + 7]) ^ ((Fxi)(t) = (Fx2)(t) Vt £ [a,a + 7]).
Свойство вольтерровости оператора F позволяет рассматривать решение данного уравнения, определенное не на всем [a, b] , а на его части — отрезке [a,a + 7] , 7 £ (0, b — a), и определить понятие продолжения решения. Вот почему уравнение с вольтерровым оператором F называют эволюционным [13]. Предлагаемые численные методы решения такого уравнения используют специфику вольтеррового оператора F и являются эволюционными в том смысле, что значение решения вычисляются постепенно при все больших значениях аргументов. Таким свойством обладают, например, известные методы решения обыкновенных дифференциальных уравнений (методы Эйлера, Рунге-Кутты, Адамса).
1. Метод Тонелли
На примере метода Тонелли, известного для обыкновенных дифференциальных уравнений (см., например, [14]), удобно проследить основную идею многих эволюционных методов приближенного решения уравнений с последействием.
Рассмотрим задачу Коши
X(t) = (GHx)(t), t £ [a,b], x(a) = а. (1)
Здесь операторы H : ACp[a,b] ^ Lr[a,b], G : Lr[a,b] ^ Lp[a,b] вольтерровы. Разобьем
отрезок [a,b] на к равновеликих частей точками a, a + Tk, a + 2r^, b (тk = )■
Алгоритм состоит в замене оператора H оператором Hk : ACp[a,b] ^ Lr[a,b] ,
Вследствие т -вольтерровости оператора Hk решение Xk задачи
Xk(t) = (GHkXk)(t), t £ [a,b], Xk(a) = а, (2)
находится по формулам
xk(t) = а + f(G0)(s)ds, если t £ [a,a + Tk];
Xk(t) = (xk)(a + iTk)+ f (GHkXk)(s)ds, (3)
если t £ [a + iTk,a + (i + 1)Tk], i = 0, 1. k — 1.
Достаточные условия сходимости метода Тонелли предоставляет следующее утверждение.
Теорема 1. Пусть операторы H : ACp[a, b] ^ Lr [a, b], G : Lr [a, b] ^ Lp[a, b] непрерывны, ограничены и хотя бы один из них является вполне непрерывным. Пусть, далее, для решений Xk задач (2) при любом к выполнено неравенство \\Xk\\acv х1 при І£ [tl,t2),
х2 = х1 + / (Тyl)(s)ds,
хі = хі-1 + / (ТУі-1 )(,з)сІ,в. ІІ— 1
Пример 1. Найдем приближенное решение задачи
х(Ь) = х2(-) — 4 + 1, Ье [0,1], х(0) = 0. (8)
Предварительно проверим выполнение условий теоремы 2. Оператор Т, определяемый равенством (Ту)(Ь) = у2(|) —14 + 1, переводит каждое ограниченное множество пространства 1^2р[а,Ъ] в ограниченное множество пространства Ьр[а,Ъ] и непрерывен [15]. Из результатов работы [16] следует однозначная разрешимость задачи (8). Сравним точное решение задачи (8) х = Ь с приближенным решением, найденным по формулам (7). Возьмем к = 10, т = 0,1, получим
х1 = (—— + 1)dі = 0, 0999,
х2 = 0, 0999 + (-— + 1)dі = 0,1993,
хз = 0,1993 + (0, 09992 — — + 1)dі = 0, 3078,
х10 = 0, 9034 + (0, 80432 — 4 + 1^і = 0, 9980.
Теперь применим формулу (7) к численному интегрированию задачи Коши для обыкновенного дифференциального уравнения
х(Ь) = /(Ь,х(Ь)), Ь Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Хг = Х—1 + J / (8,Хг-г)“8, I = 1, 2. к.
Если функция / : [а,Ь] х Я ^ Я непрерывна по совокупности аргументов, то для вычисления интегралов можно воспользоваться методом прямоугольников. Тогда
Хг = Хг-1 + Тк ■ /(г-1, Хг-1), г = 1,2,к.
Таким образом, в применении к обыкновенному дифференциальному уравнению предлагаемый метод аналогичен известному методу Эйлера.
Отметим, в заключение, что если для любого х Е АСр[а, Ь] функция (ТРкх)(Ь) кусочно
непрерывна на интервале (Ьг-1,Ьг), то интеграл в формуле (7) можно вычислить прибли-
женно методом прямоугольников. В этом случае получаем
Хг = Хг-1 + Тк ■ (Ту-Щ-г). (9)
3. Улучшенный метод Эйлера
В основе рассмотренных методов лежит идея замены задачи Коши (5) «приближенной задачей», эквивалентной уравнению с т -вольтерровым оператором. Эту идею применим для распространения методов Рунге-Кутты на решение функционально-дифференциальных уравнений. Выведем формулу улучшенного метода Эйлера (метода Рунге-Кутты второго порядка). Для приближенного решения задачи (5) заменим ее задачей
Хк(Ь) = (Т[Ркх + ТкТРкх])(Ь), Ь Е [а, Ь], х(а) = а. (10)
Здесь оператор Тк : Ьр[а,Ь] ^ Ьг [а,Ь] определяется равенством (Тку)(Ь) = / Тк(Ь, 8)у(з)й8,
%(Ь,8) = ( 1 если [— ]тк + а -8 к
Хг+1 = Хг + J /(8,Хг + J /(£,Хг)“£)“,8.
= Хг + / / (8,Хг + J / (t,xг
Будем предполагать, что функция / : [а, Ь] х Я ^ Я непрерывна по совокупности аргументов. Для вычисления интегралов воспользуемся методом прямоугольников. Тогда
Хг+г = Хг + Тк ■ /(Ьг + 0, 5тк,хг + 0, 5тк/(Ьг,хг)).
Таким образом, для обыкновенных дифференциальных уравнений формула (11) является формулой улучшенного метода Эйлера.
Пусть для любого х Е АСР [а,Ь] функция (ТРкх)(Ь) кусочно непрерывна на интервале (и,и+\). В этом случае определенные интегралы в формуле (11) можно приближенно вычислить с помощью метода прямоугольников. Тогда решение задачи (10) запишется в виде
у0(8) = а, у0(8) = а + 0, 5тк(Ту0)(а), 8Е [а,Ьг],
Хг = а + Тк(Ту0)(а + 0, 5тк);
(8) = \ Уг-г(8), если 8 Е [a,tг],
\ Хг, если 8 Е (и,к+г],
уг-г(8), если 8Е [а,Ьг], (12)
уг(8 1 хг + 0, 5тк(Туг)(Ьг), если 8Е (Ьг,Ьг+г],
Хг+г = хг + Тк(Туг)(Ьг + 0, 5тк).
Пример 2. Применим формулы метода Эйлера и улучшенного метода Эйлера для численного решения задачи
Х(Ь) = 4у х ^2^ — 2, Ь £ [0,1], х(0) = 1.
Эта задача имеет единственное решение х = (Ь + 1)2. Вычисления будем производить по формулам (9) и (12), взяв к = 10, т = 0,1.
Ь£ [0; 0,1] хх = 1 + 0,1 (4л/1 — 2) = 1,2; t £ (0,1; 0,2] Х2 = 1,2 + 0,1 (4^1 — 2) = 1,4;
t £ (0,2; 0,3] Хз = 1,4 + 0,1 (4^1,2 — 2) = 1,638.
И т. д., полностью результаты счета приведены в табл. 1.
2. Улучшенный метод Эйлера.
Уо(з) = 1, уо(з) = 1 + 0,05 (4у/1 — 2) = 1,1; 5£ [0; 0,1],
Хх = 1 + 0,1 (4^/1Д — 2) ^ 1,2195;
Ух(в)^ 1,2195; у1(в) = 1,2195 + 0,05 (4л/1 — 2) = 1,3195; ¿£ [0,1; 0,2),
Х2 = 1,2195 + 0,1 (4^1! — 2)^ 1,4390;
У2(в) = 1, 4390; у2(в) = 1,4390 + 0,05 (4^/ 1,2195 — 2)^ 1,5598; й£ [0,2; 0,3),
уз = 1,4390 + 0,1 (4^1,3195 — 2) = 1,6985.
И т. д., полностью результаты вычислений приведены в табл. 1.
Решение задачи Х(Ь) = 4 у х ^2^ — 2 , t £ [0, 1] , х(0) = 1, методом Эйлера и улучшенным методом Эйлера
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
Метод Эйлера 1,200 1,400 1,638 1,838 2,111 2,385 2,697 3,009 3,351 3,693
метод Эйлера 1,2195 1,4390 1,6985 1,9580 5 5 ,2 2, 2,5571 6 6 9 ,8 2, 1 6 3 ,2 3, 3,6155 3,9948
Точное решение 1,21 1,44 1,69 1,96 2,25 2,56 2,89 3,24 3,61 4,00
1 . Азбелев Н.В., Смолин И.М., Цалюк З.Б. Об одном приближенном методе построения функции
Коши // Доклады АН СССР. 1960. Т. 135. № 3. С. 511-514.
2 . Жуковская ТВ, Жуковский Е.С. Формула для вычисления значений функции Коши //
Функц. дифференц. уравнения и их приложения. Пермь: Изд-во Пермского политехн. ин-та, 1988. С. 34.
3 . Жуковская Т.В. Интерполяция функции Коши // Вестник Тамбовского университета. Серия
Естественные и технические науки. Тамбов, 2002. Т. 7. Вып. 1. С. 110-111.
4 . Жуковская Т.В. Метод построения функции Коши уравнения с обобщенно вольтерровым опе-
ратором // Вестник Тамбовского университета. Серия Естественные и технические науки. Тамбов, 2003. Т. 8. Вып. 1. С. 162-163.
5 . Юганова С.А. К вопросу о приближенном построении оператора Коши. Пермь, 1981. 11 с.
Деп. в ВИНИТИ, № 3820-81.
6 . Жуковская Т.В. О приближенных методах решения задачи Коши // Современ. методы теории
краев. задач. Воронеж: Изд-во Воронежского гос. ун-та, 2005. С. 59.
7. Жуковская ТВ, Жуковский Е.С. Численные методы решения функциональнодифференциальных уравнений // Функц. дифференц. уравнения. Пермь: Изд-во Пермского политехн. ин-та, 1988. С. 110-113.
8 . Жуковская Т.В, Жуковский Е.С. Об уравнении Риккати // Современные проблемы механики
и прикладной математики. Воронежская математическая школа. Воронеж, 1998. С.116.
9 . Драхлина Н.Ш. О сходимости одного приближенного метода решения функционально-
дифференциального уравнения // Краевые задачи. Пермь: Изд-во Перм. политех. ин-та, 1988. С. 82-87.
10 . Жуковский Е.С. О параметрическом задании решения дифференциального уравнения и его
приближенном нахождении // Известия ВУЗов. Математика. 1995. № 4 (407). С. 31-34.
11 . Жуковская Т.В, Молоканова Е.А., Стуров Д.Л. О вертикальных асимптотах интегральных
кривых обыкновенных дифференциальных уравнений // Вестник Тамбовского гос. техн. ун-та. Тамбов, 2011. Т. 17. № 3. С. 744-751.
12 . Тихонов А.Н. О функциональных уравнениях типа Вольтерра и их применениях к некоторым
задачам математической физики // Бюл. Москов. ун-та. Секц. А. 1938. Т. 1. Вып. 8. С. 1-25.
13 . Азбелев Н.В., Березанский Л.М., Рахматуллина Л.Ф. О линейном функционально-
дифференциальном уравнении эволюционного типа // Дифференциальные уравнения. 1977. Т. 13. № 11. С. 1915-1925.
14 . Мамедов Я.Д. Приближенные методы решения обыкновенных дифференциальных уравнений.
Баку: МААРИФ, 1974. 176 с.
15 . Данфорд Н., Шварц Дж. Линейные операторы. Общая теория. М: Едиториал УРСС, 2004.
16 . Азбелев Н.В., Максимов В.П. Априорные оценки решений задачи Коши и разрешимость кра-
евых задач для уравнений с запаздывающим аргументом // Дифференциальные уравнения. 1979. Т. 15. № 10. С. 1731-1749.
БЛАГОДАРНОСТИ: Работа выполнена при поддержке РФФИ (проект № 11-01-00645) и Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России на 2009-2013 годы».
Поступила в редакцию 28 сентября 2012 г.
Zhukovskaya T.V., Molokanova E.A. NUMERICAL METHODS FOR SOLUTION OF EVOLUTIONARY FUNCTIONAL-DIFFERENTIAL EQUATIONS
General method for construction of approximate solution to the Cauchy problem for evolutionary functional-differential equation is described. Analogs of the Euler method and the Runge-Kutta method for numerical methods of solution of evolutionary functional-differential equations are given on the basis of this method. Conditions for convergence of methods are presented.
Key words: Volterra operator; t-Volterra operator; functional-differential equation; Cauchy problem; approximate solution; numerical methods.
Численное решение математических моделей объектов заданных системами дифференциальных уравнений
Введение:
При математическом моделировании ряда технических устройств используются системы дифференциальных нелинейных уравнений. Такие модели используются не только в технике, они находят применение в экономике, химии, биологии, медицине, управлении.
Исследование функционирования таких устройств требуют решения указанных систем уравнений. Поскольку основная часть таких уравнений являются нелинейными и нестационарными, часто невозможно получить их аналитическое решение.
Возникает необходимость использовать численные методы, наиболее известным из которых является метод Рунге — Кутты [1]. Что касается Python, то в публикациях по численным методам, например [2,3], данных по применение Рунге — Кутты крайне мало, а по его модификации — методу Рунге-Кутта-Фельберга вообще нет.
В настоящее время, благодаря простому интерфейсу, наибольшее распространение в Python имеет функцию odeint из модуля scipy.integrate. Вторая функция ode из этого модуля реализует несколько методов, в том числе и упомянутый пятиранговый метод Рунге-Кутта-Фельберга, но, вследствие универсальности, имеет ограниченное быстродействие.
Целью настоящей публикации является сравнительный анализ перечисленных средств численного решения систем дифференциальных уравнений с модифицированным автором под Python методом Рунге-Кутта-Фельберга. В публикации так же приведены решения по краевым задачам для систем дифференциальных уравнений (СДУ).
Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
Для одного дифференциального уравнения n – го порядка, задача Коши состоит в нахождении функции, удовлетворяющей равенству:
и начальным условиям
Перед решением эта задача должна быть переписана в виде следующей СДУ
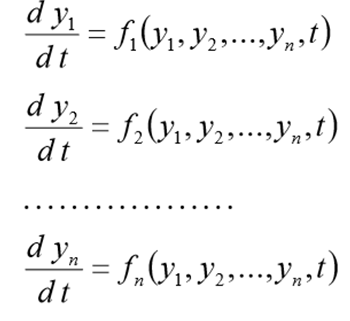
с начальными условиями
Модуль имеет две функции ode() и odeint(), предназначенные для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (задача Коши). Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.
Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат odeint(func, y0, t[,args=(), . ]) Аргумент func – это имя Python функции двух переменных, первой из которых является список y=[y1,y2. yn], а второй – имя независимой переменной.
Функция func должна возвращать список из n значений функций 
Второй аргумент y0 функции odeint() является массивом (или списком) начальных значений 
Третий аргумент является массивом моментов времени, в которые вы хотите получить решение задачи. При этом первый элемент этого массива рассматривается как t0.
Функция odeint() возвращает массив размера len(t) x len(y0). Функция odeint() имеет много опций, управляющих ее работой. Опции rtol (относительная погрешность) и atol (абсолютная погрешность) определяют погрешность вычислений ei для каждого значения yi по формуле
Они могут быть векторами или скалярами. По умолчанию
Вторая функция модуля scipy.integrate, которая предназначена для решения дифференциальных уравнений и систем, называется ode(). Она создает объект ОДУ (тип scipy.integrate._ode.ode). Имея ссылку на такой объект, для решения дифференциальных уравнений следует использовать его методы. Аналогично функции odeint(), функция ode(func) предполагает приведение задачи к системе дифференциальных уравнений вида (1) и использовании ее функции правых частей.
Отличие только в том, что функция правых частей func(t,y) первым аргументом принимает независимую переменную, а вторым – список значений искомых функций. Например, следующая последовательность инструкций создает объект ODE, представляющий задачу Коши.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
При численном решении задачи Коши
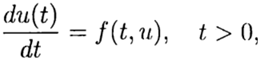

по известному решению в точке t =0 необходимо найти из уравнения (3) решение при других t. При численном решении задачи (2),(3) будем использовать равномерную, для простоты, сетку по переменной t с шагом т > 0.
Приближенное решение задачи (2), (3) в точке 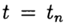

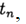


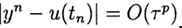

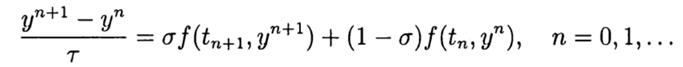
При 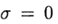
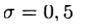
Явные схемы второго и более высокого порядка аппроксимации удобно строить, ориентируясь на метод предиктор-корректор. На этапе предиктора (предсказания) используется явная схема
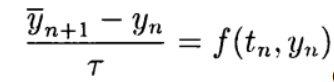
а на этапе корректора (уточнения) — схема
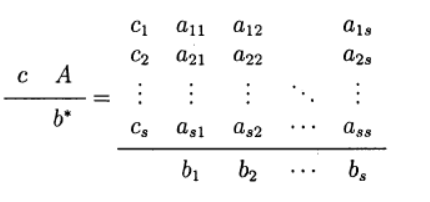
В одношаговых методах Рунге—Кутта идеи предиктора-корректора реализуются наиболее полно. Этот метод записывается в общем виде:

Формула (6) основана на s вычислениях функции f и называется s-стадийной. Если 
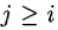

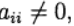

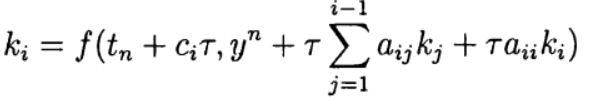
О таком методе Рунге—Кутта говорят как о диагонально-неявном. Параметры 
Одним из наиболее распространенных является явный метод Рунге—Кутта четвертого порядка

Метод Рунге—Кутта— Фельберга
Привожу значение расчётных коэффициентов 
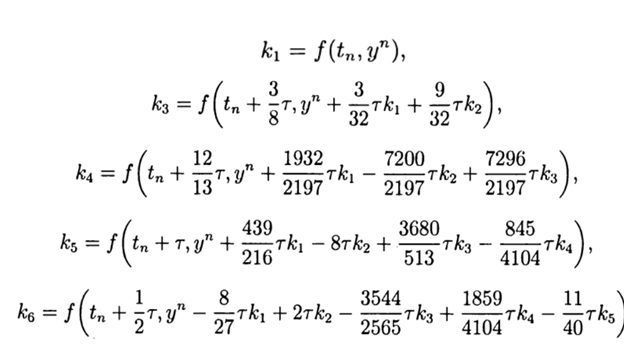
С учётом(9) общее решение имеет вид:
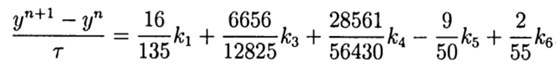
Это решение обеспечивает пятый порядок точности, остаётся его адаптировать к Python.
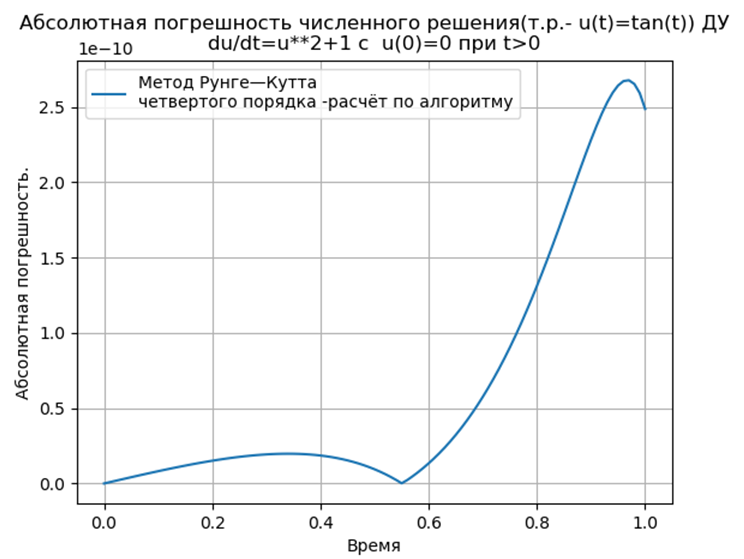
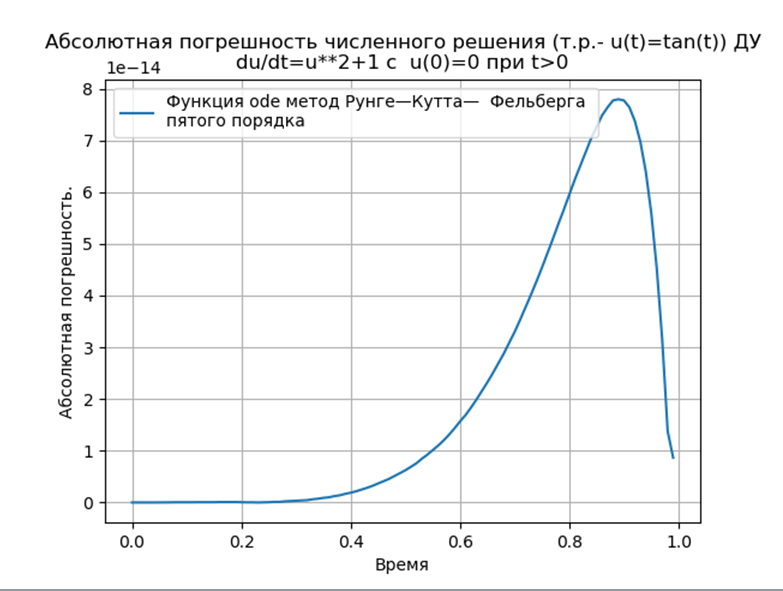
Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения  с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
Адаптированные к Python методы Рунге—Кутта и Рунге—Кутта— Фельберга имеют меньшую абсолютную, чем решение с применением функции odeint, но большую, чем с использованием функции edu. Необходимо провести исследование быстродействия.
Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
Сравнительный анализ проведём на примере модельной задачи, приведенной в [2]. Чтобы не повторять источник, приведу постановку и решение модельной задачи из [2].
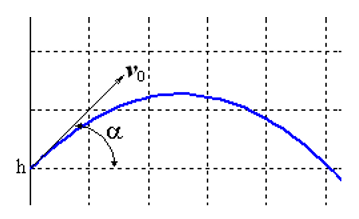
Решим задачу Коши, описывающую движение тела, брошенного с начальной скоростью v0 под углом α к горизонту в предположении, что сопротивление воздуха пропорционально квадрату скорости. В векторной форме уравнение движения имеет вид
где 



Особенность этой задачи состоит в том, что движение заканчивается в заранее неизвестный момент времени, когда тело падает на землю. Если обозначить 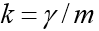
К системе следует добавить начальные условия: 

Для модельной задачи положим 
Flight time = 1.2316 Distance = 5.9829 Height =1.8542
Flight time = 1.1016 Distance = 4.3830 Height =1.5088
Flight time = 1.0197 Distance = 3.5265 Height =1.2912
Flight time = 0.9068 Distance = 2.5842 Height =1.0240
Время на модельную задачу: 0.454787
Для реализации средствами Python численного решения СДУ без использования специальных модулей, мною была предложена и исследована следующая функция:
def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6
Функция increment(f, t, y, tau) обеспечивает пятый порядок численного метода решения. Остальные особенности программы можно посмотреть в следующем листинге:
Время на модельную задачу: 0.259927
Предложенная программная реализация модельной задачи без использования специальных модулей имеет почти в двое большее быстродействие, чем с функцией ode, однако нельзя забывать, что ode имеет более высокую точность численного решения и возможности выбора метода решения.
Решение краевой задачи с поточно разделёнными краевыми условиями
Приведем пример некоторой конкретной краевой задачи с поточно разделенными краевыми условиями:
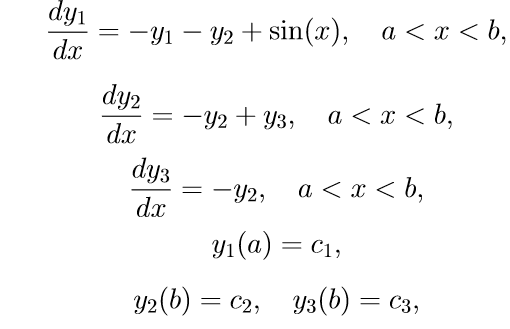
Для решения задачи (11) используем следующий алгоритм:
1. Решаем первые три неоднородные уравнения системы (11) с начальными условиями 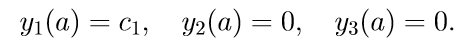
Введем обозначение для решения задачи Коши:
2. Решаем первые три однородные уравнения системы (11) с начальными условиями 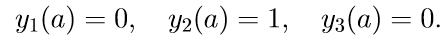
Введем обозначение для решения задачи Коши:
3. Решаем первые три однородные уравнения системы (11) с начальными условиями
Введем обозначение для решения задачи Коши:
4. Общее решение краевой задачи (11) при помощи решений задач Коши записывается в виде линейной комбинации решений: 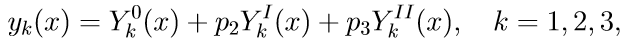
где p2, p3 — некоторые неизвестные параметры.
5. Для определения параметров p2, p3, используем краевые условия последних двух уравнений (11), то есть условия при x = b. Подставляя, получим систему линейных уравнений относительно неизвестных p2, p3:

Решая (12), получим соотношения для p2, p3.
По приведенному алгоритму с применением метода Рунге—Кутта—Фельберга получим следующую программу:
y0[0]= 0.0
y1[0]= 1.0
y2[0]= 0.7156448588231397
y3[0]= 1.324566562303714
y0[N-1]= 0.9900000000000007
y1[N-1]= 0.1747719838716767
y2[N-1]= 0.8
y3[N-1]= 0.5000000000000001
Время на модельную задачу: 0.070878
Вывод
Разработанная мною программа отличается от приведенной в [3] меньшей погрешностью, что подтверждает приведенный в начале статьи сравнительный анализ функции odeint с реализованным на Python метода Рунге—Кутта—Фельберга.
3. Н.М. Полякова, Е.В. Ширяева Python 3. Создание графического интерфейса пользователя (на примере решения методом пристрелки краевой задачи для линейных обыкновенных дифференциальных уравнений). Ростов-на-Дону 2017.
http://cyberleninka.ru/article/n/chislennye-metody-resheniya-evolyutsionnyh-funktsionalno-differentsialnyh-uravneniy
http://habr.com/ru/post/418139/
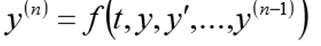
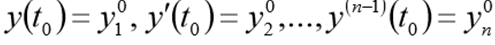


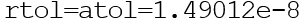
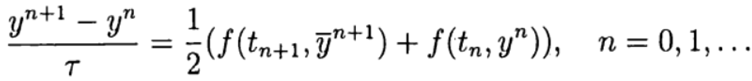
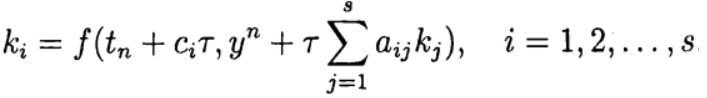
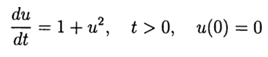 с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга