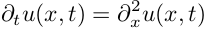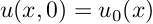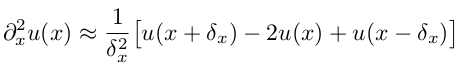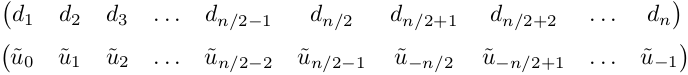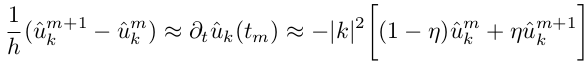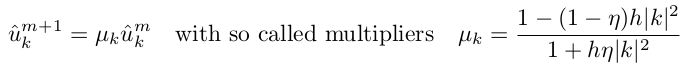Численный метод решения волнового уравнения

Численный метод решения обратной задачи для волнового уравнения в среде с локальной неоднородностью Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Головина С.Г., Захаров Е.В.

Для волнового уравнения рассматривается обратная задача определения границы локальной неоднородности по измерениям поля в ограниченной области расположения приемников в трехмерной среде. Задача сведена к системе интегральных уравнений . В работе предлагается итерационный метод решения обратной задачи и приводятся результаты вычислительных экспериментов.

A numerical method for solving the inverse problem for the wave equation in a medium with local non-homogeneity

We consider the inverse problem for wave equation to determine the boundaries of the local non-homogeneity of the field measurements in the limited area of receivers location in three-dimensional environment. The problem is reduced to the system of integral equations . This paper proposes an iterative method for solving the inverse problem and the results of computational experiments.

Текст научной работы на тему «Численный метод решения обратной задачи для волнового уравнения в среде с локальной неоднородностью»

С. Г. Головин^, Е. В. Захаров2

ЧИСЛЕННЫЙ МЕТОД РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ ДЛЯ ВОЛНОВОГО УРАВНЕНИЯ В СРЕДЕ С ЛОКАЛЬНОЙ НЕОДНОРОДНОСТЬЮ*

Для волнового уравнения рассматривается обратная задача определения границы локальной неоднородности по измерениям поля в ограниченной области расположения приемников в трехмерной среде. Задача сведена к системе интегральных уравнений. В работе предлагается итерационный метод решения обратной задачи и приводятся результаты вычислительных экспериментов.

Ключевые слова: волновое уравнение, уравнение Гельмгольца, неоднородная среда, интегральные уравнения, численный метод.

1. Введение. Граничная задача для волнового уравнения является классической моделью при изучении рассеяния акустических волн локальным включением. Подобные задачи получили широкое распространение в инженерной геофизике, акустике океана, сейсморазведке, дефектоскопии, физике атмосферы, медицине и многих других областях.

В работе исследуется среда, в которой распространение акустических колебаний описывается источниками с временной зависимостью exp(—iut) и рассеяние волн описывается уравнением Гельмгольца. Решение прямой задачи для уравнения Гельмгольца методом интегральных уравнений было предложено в 1. В данной работе рассмотрена задача распространения акустических волн в трехмерной однородной среде, содержащей локальную неоднородность с гладкой поверхностью. Обратная задача состоит в определении поверхности, являющейся границей неоднородности по измерениям отраженного от неоднородности волнового поля, возбуждаемого точечными источниками. Такая постановка задачи распространена в задачах акустического зондирования.

2. Постановка задачи. Рассмотрим распространение акустических волн в трехмерной безграничной однородной среде fio, содержащей односвязную ограниченную область !1[ £ й3 с достаточно гладкой границей díl\ — локальную неоднородность. Однородная среда fio имеет постоянное значение скорости распространения волн со, а в области fii определена кусочно-гладкая функция с(М), где М = (x,y,z). Неоднородность облучается различными точечными источниками Mf = (xf,yf,Zf), расположенными в ограниченной области пространства fi/. Измерение поля, рассеянного неоднородностью, может проводиться лишь в пределах области приема fip. Границы всех областей не имеют общих точек.

Распространение акустических волн малой амплитуды можно описать с помощью волнового уравнения [5, 6]:

AF(M, t) — = F(t)S(M — Mf),

где А — оператор Лапласа, F(M, t) — поле в среде, зависящее от пространственной переменной М(ж, у, z) € i?3, t ^ 0, с(М) — скорость распространения волны в среде, S(-) — дельта-функция Дирака, F(t)S(M — Mf) — функция источника.

В предположении, что распространение акустических волн является установившимся (с временной зависимостью exp(^¿o;í)), поставим следующую граничную задачу для уравнения Гельмгольца:

Av(M) + kjv(M) = 0, Mefi i, ^

1 Факультет BMK МГУ, ст. преп., к.ф.-м.н., e-mail: sgolovina-msuQmail.ru

2 Факультет BMK МГУ, проф., д.ф.-м.н., e-mail: zspecQcs.msu.ru

* Работа выполнена при финансовой поддержке РФФИ, проект № 17-01-00525.

с условиями сопряжения на границе 1

и условиями излучения Зоммерфельда на бесконечности (при г = у/./-1′ + //- + г1′ оо)

где у(М) = у(М,ш) — поле давления, [-]ап! — скачок значения функции на границе раздела сред,

п — внешняя нормаль к границе, ко = —, кЛМ) = ——-. Функцию источника можно аппрок-

симировать дельта-функцией /(ш)6(М — М/), где /(ш) — амплитуда поля, Mf — координаты источников поля, ш — частота. Эта аппроксимация основывается на предположении о малости линейных размеров источников в сравнении с масштабом решаемой задачи.

Введем новую функцию с(М) = с^2 — с

2(М), тогда с(М) = со^— с(М)сд и запишем

уравнение (1) в виде

АУ(М) + к$у(М) = ¡(ш)8(М — Мг) + ш2у(М)с(М). (2)

В этом уравнении правая часть состоит из источников первичного поля и источников вторичного поля ш2’о<М)с<М). Полное поле в уравнении (2) можно представить как сумму первичного и вторичного полей: и(М) = г>о(М) + у\(М). Функции г>о(М) и (М) удовлетворяют уравнениям Гельмгольца с разными правыми частями:

АУО(М) + к?ММ) = ¡(ш)5(М — МД

Д«1 (М) + ф! (М) = ш2у(М)с(М).

Заметим, что первичное и вторичное поля удовлетворяют условиям излучения Зоммерфельда на бесконечности. Используя функцию Грина

0(М, Р) = —I-ехр \i-RMP

где г>о(М) = ] £?(М, Р)/(ш)5(Р — М/) йР имеет физический смысл волны, излучаемой источником

в однородной среде.

Запишем уравнение (4) для случаев, когда М принадлежит локальной неоднородности П1 и области расположения приемников Пр (см. рис. 1):

V!(М) = иг I 0(М, Р)с(Р)у(Р)ёР, М е пр.

Интегрирование проводится по локальной области П1 С Д3, где функция с(М) отлична от нуля. Система (5) является нелинейной относительно функций с(М) и и(М) при М ё 01.

При решении прямой задачи, когда граница неоднородности П1 известна и соответственно известна функция с(М), М е П1, необходимо решить интегральное уравнение Фредгольма второго рода и найти функцию г>(М), М € О1, далее вычислить значение функции (М), М € Ор,

12 ВМУ, вычислительная математика и кибернетика, № 4

Рис. 1. Расположение исследуемых областей: 1 область расположения источников; 2 область расположения приемников; 3 область с локальным включением

используя систему (5) (при фиксированном источнике). Заметим, что при решении обратной задачи использование в вычислениях нескольких частот ш или нескольких источников существенно для единственности решения обратной задачи. В работе [7] приводится пример, когда решение системы (5) не единственно, если измерения рассеянного поля проводятся на одной частоте и при одном источнике.

Для проверки предложенной модели распространения акустических волн в однородной среде. содержащей сферическую локальную неоднородность, в работе [8] были проведены модельные расчеты. Наличие сферической симметрии позволяет применить для решения прямой задачи метод разделения переменных и использовать представление искомого поля в виде разложения в ряд по собственным функциям волнового оператора, построить решение в аналитической форме и сравнить полученные результаты с модельными расчетами. Выполненные расчеты показали достаточно хорошее совпадение решений прямой задачи аналитическим методом и методом интегральных уравнений, погрешность отклонения составила не более 2%.

Разработка численных методов решения обратной задачи, когда неизвестными являются функции с(М) и г>(М), М € Оь встречает ряд трудностей: данные и решение лежат в разных областях, различные размерности множества входных данных и решения, не выполнены обычные условия регулярности [9, 10].

В работе [11] рассмотрен абстрактный аналог системы (5) в виде операторного уравнения -Р(г) = 0, где оператор Р действует из гильбертова пространства И\ в другое гильбертово

пространство Н2, г = (у(М), с(М)) вектор неизвестных. Для решения использован метод Ньютона Гаусса [12]:

где Р’п = Р'(гп). В итеративно-регуляризованном варианте метода Ньютона Гаусса на каждом шаге минимизируется по г функционал

где ап параметр регуляризации, £„ некоторый элемент Н\. Тогда итерационный процесс можно записать в следующем виде:

• 1 — ( ¡’Ц РЦ «Ь » / (М) = О, М е Оь

К2(у,с) = со2 I 0(М, Р)с(Р)у(Р) ЛР — гч(М) = О,

где V = г>(М), с = с(М).

Для решения этой задачи будем использовать следующий итерационный процесс:

1) зададим начальное приближение с0 = 0 для функции с;

2) решив уравнение К1 (г’°, с0) = 0 стандартным методом, найдем функцию г>°;

3) решив уравнение Е^Ас1) = 0 регуляризованным методом Ньютона Гаусса, найдем с1;

4) решив уравнение А’^Дс1) = 0, найдем функцию V1 и т.д.

На каждом шаге предложенного итерационного процесса приходится численно решать интегральное уравнение, что замедляет скорость вычисления итераций, но позволяет на порядок снизить размерность обрабатываемых массивов. Отметим, что первый шаг процесса совпадает с решением обратной задачи в борновском приближении, когда отраженное от неоднородности поле заменяется первичным. Нахождение функции с(Р) сводится к решению уравнения Фредгольма первого рода:

гч (М) =ш2 I С(М, Р)с(Р)г>0(Р) ЛР.

Приведем результаты модельных расчетов, где в качестве входных данных использовалось решение прямой задачи с внесенной погрешностью 5%. Два источника располагались в области Q,f в точках с координатами (0, 0, 271) и (200, 200, 271), измерения проводились на сетке приемников 25 х 25, расположенных в области

5. Горюнов A.A., Сасковец A.B. Обратные задачи рассеяния в акустике. М.: Изд-во МГУ, 1989.

6. Жданов М. С. Теория обратных задач и регуляризации в геофизике. М.: Научный мир, 2007.

7. Davaney A. J. Nonuniqueness in the inverse scattering problem //J. Math. Phys. 1978. 19. N 7. P. 15261531.

8. Головина С. Г., Никитина Е. В. Численный анализ методов определения спектральной амплитуды акустического поля // Вестн. Моск. ун-та. Сер. 15. Вычиел. матем. и киберн. 1997. № 3. С. 20-23. (Golovina S.G., Nikitina Е. Numerical analysis of methods for determining the spectrial amplitude of the acoustic field // Moscow Univ. Comput. Math, and Cybern. 1997. 15. N 3. P. 20-23.)

9. Тихонов A.H., Ареенин В.Я. Методы решения некорректных задач. М.: Наука, 1986.

10. Рамм А. Г. Многомерные обратные задачи рассеяния. М.: Мир, 1994.

11. Бакушинский А.Б., Левитан С.Ю. Некоторые модели и численные методы нелинейной вычислительной диагностики // Сборник трудов ВНИИСИ АН СССР. Вып. 13. М.: Изд-во ВНИИСИ, 1991. С. 3-25.

Волновое уравнение

Одним из наиболее распространенных в инженерной практике уравнений с частными производными второго порядка является волновое уравнение, описывающее различные виды колебаний. Поскольку колебания — процесс нестационарный, то одной из независимых переменных является время t. Кроме того, независимыми переменными в уравнении являются также пространственные координаты х, у, z. В зависимости от их количества различают одномерное, двумерное и трехмерное волновые уравнения.

Одномерное волновое уравнение – уравнение, описывающее продольные колебания стержня, сечения которого совершают плоскопараллельные колебательные движения, а также поперечные колебания тонкого стержня (струны) и другие задачи. Двумерное волновое уравнение используют для исследования колебаний тонкой пластины (мембраны). Трехмерное волновое уравнениеописывает распространение волн в пространстве (например, звуковых волн в жидкости, упругих волн в сплошной среде и т.п.).

Рассмотрим одномерное волновое уравнение, которое можно записать в виде

(2.63)

Для поперечных колебаний струны искомая функция U(x,t) описывает положение струны в момент t. В этом случае а2 = Т/ρ, где Т — натяжение струны, ρ — ее линейная (погонная) плотность. Колебания предполагаются малыми, т.е. амплитуда мала по сравнению с длиной струны. Кроме того, уравнение (2.63) записано для случая свободных колебаний. В случае вынужденных колебаний в правой части уравнения добавляют некоторую функцию f(x,t), характеризующую внешние воздействия, при этом сопротивление среды колебательному процессу не учитывается.

Простейшей задачей для уравнения (2.63) является задача Коши: в начальный момент времени задаются два условия (количество условий равно порядку входящей в уравнение производной по t):

(2.64)

Эти условия описывают начальную форму струны и скорость ее точек .

На практике чаще приходится решать не задачу Коши для бесконечной струны, а смешанную задачу для ограниченной струны некоторой длины l. В этом случае задают граничные условия на ее концах. В частности, при закрепленных концах их смещения равны нулю, и граничные условия имеют вид

(2.65)

Рассмотрим некоторые разностные схемы для решения задачи (2.63)-(2.65). Простейшей является явная трехслойная схема типа крест (шаблон показан на рис. 2.21). Заменим в уравнении (2.63) вторые производные искомой функции Uпо tи х их конечно-разностными соотношениями с помощью значений сеточной функции в узлах сетки :

Рис. 2.21. Шаблон явной схемы

Отсюда можно найти явное выражение для значения сеточной функции на ( j + 1)-ом слое:

(2.66)

Здесь, как обычно в трехслойных схемах, для определения неизвестных значений на (j + 1)-ом слое нужно знать решения на j-ом и (j — 1)-ом слоях. Поэтому начать счет по формулам (2.66) можно лишь для второго слоя, а решения на нулевом и первом слоях должны быть известны. Их находят с помощью начальных условий (2.64). На нулевом слое имеем

(2.67)

Для получения решения на первом слое воспользуемся вторым начальным условием (2.64). Производную заменим конечно-разностной аппроксимацией. В простейшем случае полагают

(2.68)

Из этого соотношения можно найти значения сеточной функции на первом временном слое:

(2.69)

Отметим, что аппроксимация начального условия в виде (2.68) ухудшает аппроксимацию исходной дифференциальной задачи: погрешность аппроксимации становится порядка , т.е. первого порядка по τ, хотя сама схема (2.66) имеет второй порядок аппроксимации по hи τ. Положение можно исправить, если вместо (2.69) взять более точное представление:

(2.70)

Вместо нужно взять . А выражение для второй производной можно найти с использованием исходного уравнения (2.63) и первого начального условия (2.64). Получим

Тогда (2.70) примет вид:

(2.71)

Разностная схема (2.66) с учетом (2.71) обладает погрешностью аппроксимации порядка

При решении смешанной задачи с граничными условиями вида (2.65), т.е. когда на концах рассматриваемого отрезка заданы значения самой функции, второй порядок аппроксимации сохраняется. В этом случае для удобства крайние узлы сетки располагают в граничных точках (х0=0, xI = l). Однако граничные условия могут задаваться и для производной.

Например, в случае свободных продольных колебаний стержня на его незакрепленном конце задается условие

(2.72)

Если это условие записать в разностном виде с первым порядком аппроксимации, то погрешность аппроксимации схемы станет порядка . Поэтому для сохранения второго порядка данной схемы по hнеобходимо граничное условие (2.72) аппроксимировать со вторым порядком.

Рассмотренная разностная схема (2.66) решения задачи (2.63) — (2.65) условно устойчива. Необходимое и достаточное условие устойчивости:

(2.73)

Следовательно, при выполнении этого условия и с учетом аппроксимации схема (2.66) сходится к исходной задаче со скоростью O(h2+τ2). Данная схема часто используется в практи-ческих расчетах. Она обеспечивает приемлемую точность получения решения U(x,t), которое имеет непрерывные производные четвертого порядка.

Рис. 2.22. Алгоритм решения волнового уравнения

Алгоритм решения задачи (2.63)-(2.65) с помощью данной явной разностной схемы приведен на рис. 2.22. Здесь представлен простейший вариант, когда все значения сеточной функции, образующие двумерный массив, по мере вычисления хранятся в памяти компьютера, а после решения задачи выводятся результаты. Можно было бы предусмотреть хранение решения лишь на трех слоях, что сэкономило бы память. Результаты в таком случае можно выводить в процессе счета (см. рис. 2.13).

Существуют и другие разностные схемы решения волнового уравнения. В частности, иногда удобнее использовать неявные схемы, чтобы избавиться от ограничений на величину шага, налагаемых условием (2.73). Эти схемы обычно абсолютно устойчивы, однако алгоритм решения задачи и программа для компьютера усложняются.

Построим простейшую неявную схему. Вторую производную по tв уравнении (2.63) аппроксимируем, как и ранее, по трехточечному шаблону с помощью значений сеточной функции на слоях j— 1, j, j + 1. Производную до х заменяем полусуммой ее аппроксимации на (j + 1)-ом и (j— 1)-ом слоях (рис. 2.23):

Рис. 2.23. Шаблон неявной схемы

Из этого соотношения можно получить систему уравнений относительно неизвестных значений сеточной функции на (j+ 1)-ом слое:

(2.74)

Полученная неявная схема устойчива и сходится со скоростью . Систему линейных алгебраических уравнений (2.74) можно, в частности, решать методом прогонки. К этой системе следует добавить разностные начальные и граничные условия. Так, выражения (2.67), (2.69) или (2.71) могут быть использованы для вычисления значений сеточной функции на нулевом и первом слоях по времени.

При двух или трех независимых пространственных переменных волновые уравнения принимают вид

Для них также могут быть построены разностные схемы по аналогии с одномерным волновым уравнением. Разница состоит в том, что нужно аппроксимировать производные по двум или трем пространственным переменным, что, естественно, усложняет алгоритм и требует значительно больших объемов памяти и времени счета. Подробнее двумерные задачи будут рассмотрены ниже для уравнения теплопроводности.

Спектральный метод на примере простых задач матфизики

В этой статье описан псевдоспектральный метод численного решения уравнений матфизики, используемый в вычислительной гидродинамике, геофизике, климатологии и во многих других областях.

Одномерная задача распространения тепла по стержню

Для начала рассмотрим простую одномерную задачу распространения тепла в стержне. Уравнение, описывающее распространение тепла при некотором начальном распределении температуры по стержню:

Такое уравнение решается аналитически методом разделения переменных, например здесь, но нас интересует как это можно сделать численно. Прежде всего нужно определиться, как считать вторую пространственную производную по х. Проще всего это делается каким-нибудь разностным методом, например:

Но мы поступим иначе. Распределение температуры есть функция координаты и времени, и в каждый момент времени эта функция может быть представлена в виде суммы ряда Фурье, который в численном виде обрезается на n-ом члене:

Где u^«с крышечкой» — это коэффициенты разложения ряда Фурье. Подставим выражение для ряда в уравнение переноса тепла:

Получаем уравнение для коэффициентов Фурье, в котором отсутствует производная по координате! Теперь это обыкновенное дифференциальное уравнение, а не в частных производных, которое можно решить простым разностным методом. Уже легче, теперь остается найти коэффициенты разложения и в этом нам очень поможет быстрое преобразование Фурье (дальше FFT).

Логика здесь следующая:

1) в начальный момент времени дана функция координаты, описывающая распределение температуры по стержню;
2) разбиваем стержень на сетку из n точек;
3) находим комплексные коэффициенты Фурье с помощью алгоритма FFT, обозначим операцию как F(u);
4) умножаем полученные коэффиценты на -|k| 2 , получаем Фурье-образ второй производной. Аналогично можно получить Фурье-образ производной более высоких порядков p, достаточно умножить на (ik) p ;
5) делаем обратное преобразование Фурье F -1 (u), с помощью алгоритма IFFT, получаем значения второй производной в точках на сетке;
6) делаем шаг по времени, уже обычной разностной, явной или неявной, схемой;
7) повторяем.

Рассмотрим теперь как это работает в программе для Matlab/Octave. В качестве начального распределения температуры возьмем гладкую функцию u0=2+sin(x)+sin(2x), стержень длинной 2π разобьем на 50 точек, с шагом по времени h=0.1, граничные условия периодичные (кольцо).

Стоит отметить особенность алгоритма FFT в Matlab, связанную с тем, что полученные коэффициенты разложения на выходе d=fft(u) идут не по порядку, а смещены, первая половина на месте второй и наоборот. Cначала идут коэффициенты с номерами от 0 до n/2-1, потом с номерами от -n/2 до -1. С этим были проблемы…

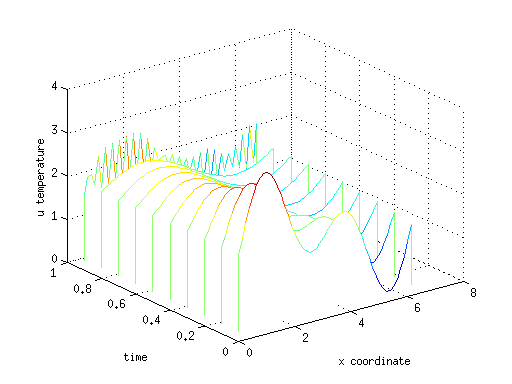
Полученное решение можно видеть на графике в виде «водопада» линий распределения температуры по х для каждого момента времени t. Видно, что решение испытывает ~~сильные осциляции~~ численную неустойчивость, связано это с невыполнением критерия Куранта. Избавиться от неустойчивости можно уменьшив шаг по времени, либо применяя более продвинутую неявную схему, например Кранка-Николсона.

Двумерное уравнение диффузии

Начальные условия: u0 = 1 + sin(2X) + cos(2Y), где u теперь 2d-массив u(i,j). Используем неявную схему интегрирования по времени (т.е. выразим m+1 шаг через m-й):

Можно доказать, что такая неявная схема никогда не расходится при η>0.5, будем использовать η=1. Таким образом каждое новое значение u m+1 получаем умножением u m на коэффициент μ_k, зависящий от временного шага и волновых чисел k, т.е. μ_k — это константа, которую не нужно пересчитывать на каждом шаге!

Двумерное волновое уравнение

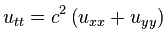
В волновом уравнении присутствует вторая производная по времени, поэтому задача сводится к системе двух обыкновенных диффуров, одна переменная — u, вторая — u_t, схему по времени в коде использовал самую простую явную, поэтому точность небольшая, шаг по времени очень маленький, зато код выглядит относительно просто. Впрочем, этого хватает для демонстрации работоспособности метода.

Периодичные граничные условия:

Фиксированные граничные условия (0 на краях, отражение волн от границ):

Выводы

В статье продемонстрировано несколько примеров применения спектрального метода для простых задач матфизики. Основная суть суть спектрального метода, это замена исходных диффренциальных уравнений в частных произодных на обыкновенные диффуры для коэффициентов разложения искомых функций по некоторому базису. Базисом могут быть синусы-косинусы, комплексные экспоненты, ортогональные полиномы, если требует геометрия — цилиндрические или сферические функции. Найденные коэффициенты в каждый момент времени позволяют восстановить искомое решение, а алгоритм FFT позволяет делать это быстро.

Преимуществами метода являются:

источники:

http://3ys.ru/metody-resheniya-differentsialnykh-uravnenij/volnovoe-uravnenie.html

http://habr.com/ru/post/267401/