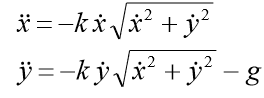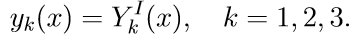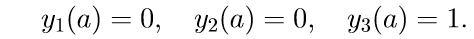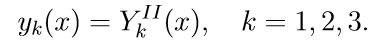Обыкновенные дифференциальные уравнения
Программа DE10 решает систему из m обыкновенных дифференциальных уравнений первого порядка yi‘(x) = fi(x, y1(x), y2(x), . ym(x)) , i=1, 2, . m методом Рунге-Кутта 4-го порядка аппроксимации с постоянным шагом без контроля точности. Предполагается, что решение системы имеет непрерывные производные до 5 порядка включительно.
Решение системы вычисляется по формулам:
call DE10(DS, A, B, N, Y)
DS, A, B, N — входные параметры;
Y — входной и выходной параметр;
DS(X, Y, DY) — процедура, которая вычисляет значения производных в точке X :
Real A, B — начальная и конечная точки интегрирования;
Integer N — число промежутков интегрирования от точки A до точки B . N должно быть >=1;
Real Y(1:m) — массив, который на входе должен содержать начальные значения функций в точке A , на выходе будет содержать решение системы в точке B .
Программа DE15 решает систему из m обыкновенных дифференциальных уравнений первого порядка yi‘(x) = fi(x, y1(x), y2(x), . ym(x)) , i=1, 2, . m методом Рунге-Кутта 5-го порядка аппроксимации с автоматическим выбором величины шага интегрирования. Предполагается, что решение системы имеет непрерывные производные до 6 порядка включительно.
Решение системы вычисляется по формулам:
На каждом шаге интегрирования системы программа вычисляет асимптотическую оценку погрешности решения:
Если погрешность оказывается меньше заданного значения ε , программа переходит к следующему шагу, если больше — программа повторяет вычисления с уменьшенной величиной шага. Величина нового шага hnew расчитывается по формуле:
5 ______
hnew = hold•√ ε/e .
call DE15(DS, X, Xout, H, Eps, Y, Error)
DS, Xout — входные параметры;
X, H, Eps, Y — входные и выходные параметры;
Error — выходной параметр;
DS(X, Y, DY) — процедура, которая вычисляет значения производных (см. прог. DE10 );
Real X, Xout — начальная и конечная точки интегрирования;
Real H — начальный шаг интегрирования, с которым программе предлагается начать вычисления. Допустимо задать абсолютное значение, даже если шаг должен быть отрицательным. На выходе переменная содержит величину шага в конце промежутка интегрирования;
Real Eps — требуемая точность интегрирования на каждом шаге;
Real Y(1:M) — массив, который на входе должен содержать начальные значения функций в точке X , на выходе будет содержать решение системы в точке Xout . Число M задает размерность решаемой системы уравнений;
Integer Error — индикатор ошибки.
Error=0 , если интегрирование системы успешно закончено и решение вычислено с заданной точностью Eps на каждом шаге;
Error=1 , если интегрирование нельзя начать, т.к. значение |Xout-X| меньше минимально-допустимой величины шага hmin , которая вычисляется программой. Параметр H приобретает значение hmin ;
Error=2 , если интегрирование нельзя начать, т.к. заданное значение Eps меньше минимально-допустимой величины εmin , которая вычисляется программой. Параметр Eps приобретает значение εmin ;
Error=65 , если программа прекратила вычисления, т.к. решение не может быть вычислено с заданной точностью Eps . Переменная X получает значение аргумента, при котором произошло прекращение вычислений. Решение в точке X должно быть вычислено правильно.
Программа DE19 вычисляет значение производной f0 и разности назад ∇f0 , ∇ 2 f0 , . ∇ k f0 порядка k в точке x0 (т.н. фронт метода), необходимые для начала интегрирования системы дифференциальных уравнений первого порядка по методу Адамса. Для нахождения этих разностей применяется алгоритм разгона, который основан на итерационном применении явных формул Адамса с последовательно увеличивающимся порядком аппроксимации. Используя начальное значение y0 в точке x0 и формулу Адамса первого порядка, вычисляем
Находим ∇f1 (1) = f1 (1) — f0 и полагаем ∇f0 = ∇f1 (1) . Используя формулу Адамса второго порядка, вычисляем
Находим f2 (2) , ∇f2 (2) , ∇ 2 f2 (2) и полагаем
Используя формулу Адамса третьего порядка, вычисляем
Последовательно применяя формулы Адамса все более высокого порядка получаем все нужные нам разности ∇f0 , ∇ 2 f0 , . ∇ k f0 до заданного порядка k включительно. Более подробную информацию об алгоритме разгона можно найти в книге [Б6].
call DE19(DS, X0, Y0, H, M, Order, DF, XH, YH, Err)
DS, X0, Y0, H, M, Order — входные параметры;
DF, XH, YH, Err — выходные параметры;
DS(X, Y, DY) — процедура, которая вычисляет значения производных (см. программу DE10 );
Real X0 — начальная точка интегрирования;
Real Y0(1:M) — начальные значения функций в точке X0 ;
Real H — шаг интегрирования;
Integer M — размерность системы дифференциальных уравнений;
Integer Order — порядок метода, который будет применен для решения системы. Значение Order должно лежть в пределах от 1 до 6;
Real DF(1:M,0:Order) — массив содержит вычисленные программой значения разностей назад в точке X0 до порядка Order включительно;
Real XH — значение аргумента, равное Order*H ;
Real YH(1:M) — вычисленное програмой значение функции в точке XH ;
Real Err — асимптотическая оценка погрешности вычисленного значаения YH .
Программа DE20 решает систему из m обыкновенных дифференциальных уравнений первого порядка yi‘(x) = fi(x, y1(x), y2(x), . ym(x)) , i=1, 2, . m методом Адамса с порядком аппроксимации от 1 до 6 без контроля точности. Предполагается, что решение системы имеет непрерывные производные на один порядок больше применяемого порядка аппроксимации.
В каждом узле интегрирования решение отыскивается по схеме прогноз-коррекция, которая заключается в следующем. Исходя из точки xn , в которой задано значение функции yn и фронт метода fn , ∇fn , ∇ 2 fn , . ∇ k-1 fn , вычисляется решение в точке xn+1=xn+h по явной формуле Адамса (прогноз):
k-1
yn+1 (p) = yn + h•∑ αj∇ j fn , (1)
j=0
где ∇ j обозначает разность назад j -го порядка, k — порядок аппроксимации. По предсказанному значению yn+1 (p) в точке xn+1 вычисляется значение производной fn+1 = f(xn+1, yn+1 (p) ) и новый фронт метода ∇fn+1 , ∇ 2 fn+1 , . ∇ k-1 fn+1 . Теперь предсказанное значение yn+1 (p) можно уточнить по неявной формуле Адамса (коррекция):
k-1
yn+1 (c) = yn + h•∑ βj∇ j fn+1 . (2)
j=0
Полученное скорректированное значение принимается за значение функции в данном узле и программа переходит к вычислениям в следующем узле и так продолжается, пока не будет достигнута конечная точка интегрирования.
Итерационный процесс (1),(2) может быть преобразован к виду [Б6]:
k-1
yn+1 (c) = yn+1 (p) — αk-1•h•∑ ∇ j fn + αk-1•h•fn+1 .
j=0
Коэффициенты αk и βk для явной и неявной формул Адамса в разностной форме для разного порядка аппроксимации k приведены в таблице 1 ниже. Увеличение поядка аппроксимации осуществляется простым добавлением новых слогаемых в формулах (1) и (2). Локальная погрешность равна коэффициенту при первом отброшенном члене суммы. В таблице 2 приведены формулы Адамса в классической форме.
| j | α | β |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 1/2 | — 1/2 |
| 2 | 5/12 | — 1/12 |
| 3 | 3/8 | — 1/24 |
| 4 | 251/720 | — 19/720 |
| 5 | 95/288 | — 3/160 |
| 6 | 19087/60480 | — 863/60480 |
| Пор | Формулы | Локаль.погр |
|---|---|---|
| Явные формулы | ||
| 1 | yn+1 = yn + hfn | (1/2)h 2 y (2) |
| 2 | yn+2 = yn+1 + (1/2)h(3fn+1 — fn) | (5/12)h 3 y (3) |
| 3 | yn+3 = yn+2 + (1/12)h(23fn+2 — 16fn+1 + 5fn) | (3/8)h 4 y (4) |
| 4 | yn+4 = yn+3 + (1/24)h(55fn+3 — 59 fn+2 + 37fn+1 — 9fn) | (251/720)h 5 y (5) |
| 5 | yn+5 = yn+4 + (1/720)h(1901fn+4 — 2774fn+3 + 2616fn+2 — 1274fn+1 — 251fn) | (95/288)h 6 y (6) |
| Неявные формулы | ||
| 1 | yn+1 = yn + hfn+1 | -(1/2)h 2 y (2) |
| 1 | yn+1 = yn + (1/2)h(fn+1 + fn) | -(1/12)h 3 y (3) |
| 2 | yn+2 = yn+1 + (1/12)h(5fn+2 + 8fn+1 = fn) | -(1/24)h 4 y (4) |
| 3 | yn+3 = yn+2 + (1/24)h(9fn+3 + 19fn+2 — 5fn+1 + fn) | -(19/720)h 5 y (5) |
| 4 | yn+4 = yn+3 + (1/720)h(251fn+4 + 646fn+3 — 264fn+2 + 106fn+1 — 19fn) | -(3/160)h 6 y (6) |
call DE20(DS, A, B, N, M, Order, Y)
DS, A, B, N, M, Order — входные параметры;
Y — входной и выходной параметр;
DS(X, Y, DY) — процедура, которая вычисляет значения производных (см. программу DE10 );
Real A, B — начальная и конечная точки интегрирования;
Integer N — число промежутков интегрирования от точки A до точки B . Значение N должно быть >= Order ;
Integer M — размерность системы дифференциальных уравнений;
Integer Order — порядок метода, который следует применить для решения системы. Значение Order должно лежть в пределах от 1 до 6;
Real Y(1:M) — массив, который на входе должен содержать начальные значения функций в точке A , на выходе будет содержать решение системы в точке B .
В процессе вычислений программа DE20 вызывает программу DE19 .
Программа DE21 решает систему из m обыкновенных дифференциальных уравнений первого порядка yi‘(x) = fi(x, y1(x), y2(x), . ym(x)) , i=1, 2, . m методом Адамса четвертого порядка аппроксимации с автоматическим выбором величины шага интегрирования. Предполагается, что решение системы имеет непрерывные производные до пятого порядка включительно.
Решение системы осуществляется по схеме прогноз-коррекция, которая изложена ранее в описании к программе DE20 .
В каждом узле интегрирования программа вычисляет погрешность полученного решения. Если погрешность оказалась меньше заданного значения ε , программа переходит к следующему узлу. Если погрешность больше ε , программа уменьшает шаг в два раза и повторяет вычисления в данном узле с уменьшенной величиной шага. В том случае, когда погрешность решения оказывается меньше, чем ε/32 несколько шагов подряд, шаг интегрирования удваивается. Вычисления продолжаются, пока не будет достигнута конечная точка промежутка.
Погрешность вычисляется на основе анализа асимптотических формул остаточных членов явного и неявного методов Адамса.
ρ (p) = y (e) — y (p) = (251/720)·h 5 ·y (v) (ξ) ≈ (251/720)·h·∇ 4 fn+1
ρ (c) = y (e) — y (c) = -(19/720)·h 5 ·y (v) (ξ) ≈ -(19/720)·h·∇ 4 fn+1
где ρ (p) и ρ (c) — погрешности явного и неявного методов, y (e) — точное решение (неизвестное), ξ — точка из промежутка ( xn , xn+1 ). Вычитая из первой формулы вторую, имеем:
y (c) — y (p) = (251/720 + 19/720)·h 5 ·y (v) (ξ) = (270/720)·h 5 ·y (v) (ξ) ,
следовательно h 5 ·y (v) (ξ) = (720/270)·(y (c) — y (p) ) . Тогда
ρ (c) = -(19/720)·(720/270)·(y (c) — y (p) ) = -(19/270)·(y (c) — y (p) ) =
= -(19/270)·(3/8)·h·∇ 4 fn+1 = -(19/720)·h·∇ 4 fn+1
Таким образом величина погрешности совпадает с остаточным членом неявной формулы Адамса.
call DE21(DS, X, Xout, H, Eps, Y, Error)
DS, Xout — входные параметры;
X, H, Eps, Y — входные и выходные параметры;
Error — выходной параметр;
DS(X, Y, DY) — процедура, которая вычисляет значения производных (см. программу DE10 );
Real X, Xout — начальная и конечная точки интегрирования;
Real H — начальный шаг интегрирования, с которым программе предлагается начать вычисления. Допустимо задать абсолютное значение, даже если шаг должен быть отрицательным. На выходе переменная содержит величину шага в конце промежутка интегрирования;
Real Eps — требуемая точность интегрирования на каждом шаге;
Real Y(1:M) — массив, который на входе должен содержать начальные значения функций в точке X , на выходе будет содержать решение системы в точке Xout . Число M задает размерность решаемой системы уравнений;
Integer Error — индикатор ошибки.
Error=0 , если интегрирование системы успешно закончено и решение вычислено с заданной точностью Eps на каждом шаге;
Error=1 , если интегрирование нельзя начать, т.к. значение |Xout-X| меньше минимально-допустимой величины шага hmin , которая вычисляется программой. Параметр H приобретает значение hmin ;
Error=2 , если интегрирование нельзя начать, т.к. заданное значение Eps меньше минимально-допустимой величины εmin , которая вычисляется программой. Параметр Eps приобретает значение εmin ;
Error=3 , если интегрирование нельзя начать, т.к. погрешность решения, определенная программой при вычислении начальных значений, меньше Eps . Чтобы начать интегрирование, нужно или увеличить величину шага H , или уменьшить значение Eps ;
Error=65 , если программа прекратила вычисления, т.к. решение не может быть вычислено с заданной точностью Eps . Переменная X получает значение аргумента, при котором произошло прекращение вычислений. Решение в точке X должно быть вычислено правильно.
В процессе вычислений программа DE21 вызывает программу DE19 .
Программа DE30 решает систему из m обыкновенных дифференциальных уравнений второго порядка yi«(x) = fi(x, y1(x), . ym(x), y1‘(x), . ym‘(x)) , i=1, 2, . m методом Рунге-Кутта 4-го порядка аппроксимации без контроля точности. Предполагается, что решение системы имеет непрерывные производные до 6 порядка включительно.
Решение системы вычисляется по формулам:
call DE30(DS2, A, B, N, Y, DY)
DS2, A, B, N — входные параметры;
Y, DY — входной и выходной параметр;
DS2(X, Y, DY, DDY) — процедура, которая вычисляет значения вторых производных в точке X :
Real A, B — начальная и конечная точки интегрирования;
Integer N — число промежутков интегрирования от точки A до точки B . N должно быть >=1;
Real Y(1:m) — массив, который на входе должен содержать начальные значения функций в точке A , на выходе будет содержать решение системы в точке B ;
Real DY(1:m) — массив, который на входе должен содержать начальные значения производных в точке A , на выходе будет содержать значения производных в точке B .
Программа DE34 вычисляет значение производной f0 , вспомогательной переменной z0 и разности назад ∇f0 , ∇ 2 f0 , . ∇ k f0 порядка k в точке x0 , необходимые для начала интегрирования системы дифференциальных уравнений второго порядка по методу Штермера. Указанные величины нходятся с помощью итерационного процесса, в котором применяются явная формула Адамса (для нахождения значения производной y0‘ ) и аналог фрмулы Адамса для уравнения второго порядка (для нахождения значения переменной z0 ):
k-1
y1‘ = y0‘ + h•∑ αj∇ j fn ,
j=0
k-1
z1 = y0 + hy0‘ + h•∑ μj∇ j fn ,
j=0
y1 = y0 + hz1 .
где αj и μj — коэффициенты этих формул, j=0, 1, . k . Применяя эти формулы раз за разом c последовательно увеличивающимся порядком к исходным данным x0 , y0 , y0 ‘, мы получаем необходимые значения для начала интегрирования системы по методу Штермера из точки x0 . Более подробную информацию об этой процедуре можно найти в книге [Б6].
call DE34(DS2, X0, Y0, DY0, H, M, Order, Z, DF, XH, YH, DYH, Err)
DS2, X0, Y0, DY0, H, M, Order — входные параметры;
Z, DF, XH, YH, DYH, Err — выходные параметры;
DS2(X, Y, DY, DDY) — процедура, которая вычисляет значения вторых производных (см. программу DE30 );
Real X0 — начальная точка интегрирования;
Real Y0(1:M), DY0(1:M) — начальные значения функции и ее первой производной в точке X0 ;
Real H — шаг интегрирования;
Integer M — размерность системы дифференциальных уравнений;
Integer Order — порядок метода, который будет применен для решения системы. Значение Order должно лежть в пределах от 1 до 6;
Real Z — вычисленное программой значение вспомогательной переменной в точке X0 ;
Real DF(1:M,0:Order) — массив содержит вычисленные программой значения разностей назад в точке X0 до порядка Order включительно;
Real XH — значение аргумента, равное Order*H ;
Real YH(1:M), DYH(1:M) — вычисленное програмой значение функции и ее первой производной в точке XH ;
Real Err — асимптотическая оценка погрешности вычисленного значаения YH .
Программа DE35 решает систему из m обыкновенных дифференциальных уравнений второго порядка yi«(x) = fi(x, y1(x), . ym(x), y1‘(x), . ym‘(x)) , i=1, 2, . m методом Штермера с порядком аппроксимации от 1 до 6 без контроля точности. Предполагается, что решение системы имеет непрерывные производные на два порядка больше применяемого порядка аппроксимации.
В каждом узле интегрирования решение отыскивается по схеме прогноз-коррекция, которая заключается в следующем. В точке xn+1=xn+h вычисляется приближенное решение по явной формуле Штермера (прогноз):
k-1
yn+1 (p) = yn + ∇yn + h 2 •∑ γj∇ j fn ,
j=0
где ∇ j обозначает разность назад j -го порядка, k — порядок аппроксимации. Полученное приближение можно уточнить, выполнив вычисления по неявной формуле Штермера (коррекция):
k-1
yn+1 (с) = yn + ∇yn + h 2 •∑ δj∇ j fn+1 .
j=0
Здесь γj и δj обозначают коэффициенты явной и неявной формул Штермера. С целью уменьшения вычислительной погрешности при интегрировании системы вводится новая переменная zn и формулы Штермера пиобретают вид:
k-1
zn+1 (p) = zn + h•∑ γj∇ j fn ,
j=0
k-1
zn+1 (c) = zn + h•∑ δj∇ j fn+1 ,
j=0
yn+1 (c) = yn + hzn+1 (c) .
Значения первой производной, также как и в программе DE20 , вычисляются по схеме прогноз-коррекция по явной и неявной формулам Адамса:
k-1
yn+1‘ (p) = yn‘ + h•∑ αj∇ j fn ,
j=0
k-1
yn+1‘ (c) = yn‘ + h•∑ βj∇ j fn+1 .
j=0
Для упрощения вычислений формулы коррекции слегка видоизменяются, чтобы в их состав входили уже вычисленные предсказанные значения zn+1 (p) и yn+1‘ (p) . Окончательно вычислительный процесс выглядит следующим образом. Сначала по явным формулам вычисляются значения функции и производной в точке xn+1 :
k-1
zn+1 (p) = zn + h•∑ γj∇ j fn ,
j=0
yn+1 (p) = yn + hzn+1 (p) ,
k-1
yn+1‘ (p) = yn‘ + h•∑ αj∇ j fn .
j=0
Далее вычисляется значение fn+1=f(xn+1, yn+1 (p) , yn+1‘ (p) ) и новый фронт метода. Скорректированные значения вычисляются по формулам:
k-1
zn+1 (c) = zn+1 (p) — γk-1•h•∑ ∇ j fn + γk-1•h•fn+1 .
j=0
yn+1 (c) = yn + hzn+1 (c) ,
k-1
yn+1‘ (c) = yn+1‘ (p) — αk-1•h•∑ ∇ j fn + αk-1•h•fn+1 .
j=0
Полученные скорректированные значения принимаются за значение функции и ее производной в данном узле и программа переходит к вычислениям в следующем узле и так продолжается, пока не будет достигнута конечная точка интегрирования.
Коэффициенты γk и δk для явной и неявной формул Штермера в разностной форме для разного порядка аппроксимации k можно найти в книге [Б6].
call DE35(DS2, A, B, N, M, Order, Y, DY)
DS2, A, B, N, M, Order — входные параметры;
Y, DY — выходные параметры;
DS2(X, Y, DY, DDY) — процедура, которая вычисляет значения вторых производных (см. программу DE30 );
Real A, B — начальная и конечная точки интегрирования;
Integer N — число промежутков интегрирования от точки A до точки B . Значение N должно быть >= Order ;
Integer M — размерность системы дифференциальных уравнений;
Integer Order — порядок метода, который следует применить для решения системы. Значение Order должно лежть в пределах от 1 до 6;
Real Y(1:M), DY(1:M) — массивы, которые на входе должны содержать начальные значения функций и их первые производные в точке A , на выходе будет содержать решение системы и значения производных в точке B .
В процессе вычислений программа DE35 вызывает программу DE34 .
Программа DE23 решает систему из m обыкновенных дифференциальных уравнений первого порядка yi‘(x) = fi(x, y1(x), y2(x), . ym(x)) , i=1, 2, . m методом трапеций (неявным методом Адамса 1 порядка аппроксимации):
yn+1‘ = yn + (1/2)h(f(xn+1, yn+1) + f(xn, yn))
Для повышения устойчивости итерационный процесс для нахождения yn+1(x) выполняется по методу Ньютона.
На каждом шаге выполняется от 1 до 3 итераций. Итерации прерываются, если каждая из компонент вектоа решения становится меньше заданного числа Eps . Если после выполнения 3-х итераций какая-либо из компонент не достигла заданной точности, специальная переменная nErr увеличивается на 1. На выходе из программы эта переменная содержит общее число шагов, на которых не была достигнута заданная точность Eps .
Для реализации итераций по методу Ньютона на каждой итерации требуется обращение матрицы Якоби, что для сложных систем уравнений может быть достаточно трудоёмко. Если от итерации к итерации матрица Якоби меняется незначительно, заданием специального значения в переменной nWex можно оставить обращение матрицы только перед первой итерацией, а в остальных итерациях пользоваться уже вычисленным значением. Это позволяет значительно уменьшить объём вычислений. В некоторых случаях (для систем уравнений с постоянными коэффициентами) матрица Якоби не зависит от аргумента и функций, т.е. является числовой матрицей. Тогда матрица Якоби обращается только один раз в начале выполнения программы и далее на всём выполнении программы используется уже вычисленное значение.
В процессе вычислений программа DE23 вызывает программу AIG2R обращения матрицы.
call DE23(DS, DSJ, A, B, Y, N, Eps, met, nWex, nErr)
DS, DSJ, A, B, N, met, nWex — входные параметры;
Y, Eps — входные и выходные параметры;
nErr — выходной параметр;
DS(X, Y, DY) — процедура, которая вычисляет значения производных;
DSJ(X, Y, DYJ) — процедура, которая вычисляет значения матрицы Якоби. Частная производня от правой части i-го уравнения по j-ой переменной Y(i) запоминается в элементе DYJ(i,j) ;
Real A, B — начальная и конечная точки интегрирования;
Integer N — число промежутков интегрирования от точки A до точки B . N должно быть >=1;
Real Y(1:M) — массив, который на входе должен содержать начальные значения функций в точке A , на выходе будет содержать решение системы в точке B . Число M задает размерность решаемой системы уравнений;
Real Eps — требуемая точность интегрирования на каждом шаге; если задано значение меньшее, чем минимально-допустимое, программа увеличит его до минимально-допусимого;
Character met — метод решения уавнения: met = ‘T’ — метод трапеций, met = ‘E’ — неявный метод Эйлера;
Integer nWex — задаёт режим вычисления Якобиана, может принимать значения 0, 1 или 2; 0 — Якобиан вычисляется только один раз в начале программы; 1 — вычисляется 1 раз на кждом шаге перед первой итерацией; 2 — вычисляется перед каждой итерацией, т.е. от 1 до 3 раз на каждом шаге.
Integer nErr — счётчик количества точек, при которых за 3 итерации не удалось достигнуть заданной точности по какой-либо компоненте решения.
Программа DE23 решает систему из m обыкновенных дифференциальных уравнений первого порядка yi‘(x) = fi(x, y1(x), y2(x), . ym(x)) , i=1, 2, . m по формуле дифференцирования назад 2-го поядка аппроксимации:
yn+2‘ = (4/3)yn+1 — (1/3)yn + (2/3)hf(xn+2, yn+2)
Для повышения устойчивости итерационный процесс для нахождения yn+2(x) выполняется по методу Ньютона. Первый шаг программа выполняет неявным методом Эйлера. На следующих шагах предсказание начального приближения осуществляется вычислением экстраполяционного многочлена Эрмита.
На каждом шаге выполняется от 1 до 3 итераций. Итерации прерываются, если каждая из компонент вектоа решения становится меньше заданного числа Eps . Если после выполнения 3-х итераций какая-либо из компонент не достигла заданной точности, специальная переменная nErr увеличивается на 1. На выходе из программы эта переменная содержит общее число шагов, на которых не была достигнута заданная точность Eps .
Для реализации итераций по методу Ньютона на каждой итерации требуется обращение матрицы Якоби, что для сложных систем уравнений может быть достаточно трудоёмко. Если от итерации к итерации матрица Якоби меняется незначительно, заданием специального значения в переменной nWex можно оставить обращение матрицы только перед первой итерацией, а в остальных итерациях пользоваться уже вычисленным значением. Это позволяет значительно уменьшить объём вычислений. В некоторых случаях (для систем уравнений с постоянными коэффициентами) матрица Якоби не зависит от аргумента и функций, т.е. является числовой матрицей. Тогда матрица Якоби обращается только один раз в начале выполнения программы и далее на всём выполнении программы используется уже вычисленное значение.
В процессе вычислений программа DE23 вызывает программу AIG2R обращения матрицы.
call DE26(DS, DSJ, A, B, Y, N, Eps, nWex, nErr)
DS, DSJ, A, B, N, nWex — входные параметры;
Y, Eps — входные и выходные параметры;
nErr — выходной параметр;
DS(X, Y, DY) — процедура, которая вычисляет значения производных;
DSJ(X, Y, DYJ) — процедура, которая вычисляет значения матрицы Якоби. Частная производня от правой части i-го уравнения по j-ой переменной Y(i) запоминается в элементе DYJ(i,j) ;
Real A, B — начальная и конечная точки интегрирования;
Integer N — число промежутков интегрирования от точки A до точки B . N должно быть >=1;
Real Y(1:M) — массив, который на входе должен содержать начальные значения функций в точке A , на выходе будет содержать решение системы в точке B . Число M задает размерность решаемой системы уравнений;
Real Eps — требуемая точность интегрирования на каждом шаге; если задано значение меньшее, чем минимально-допустимое, программа увеличит его до минимально-допусимого;
Integer nWex — задаёт режим вычисления Якобиана, может принимать значения 0, 1 или 2; 0 — Якобиан вычисляется только один раз в начале программы; 1 — вычисляется 1 раз на кждом шаге перед первой итерацией; 2 — вычисляется перед каждой итерацией, т.е. от 1 до 3 раз на каждом шаге.
Integer nErr — счётчик количества точек, при которых за 3 итерации не удалось достигнуть заданной точности по какой-либо компоненте решения.
Программа DE53 решает задчу Коши для жесткой автономной системы из m обыкновенных дифференциальных уравнений первого порядка yi‘(x) = fi(y1(x), y2(x), . ym(x)) , i=1, 2, . m методом типа Розенброка 3-го порядка аппроксимации с автоматическим выбором величины шага интегрирования. В случае неавтономной системы y’ = f(x, y(x)) введением дополнительной переменной y’m+1 = 1 , ym+1(x0) = x0 она приводится к автономному виду.
Решение системы вычисляется по формулам:
где Dn = E + α•h•fn′ ;
E — единичная матрица; h — шаг интегрирования;
fn′ = ∂f(yn)/∂y — матрица Якоби системы;
α, β21, β31, β32, p1, p2, p3 — числовые коэффициенты, определяющие свойства точности и устойчивости алгоритма.
В каждом узле интегрирования программа вычисляет погрешность полученного решения. Для оценки погрешности используется идея вложенных методов, а именно, дополнительно вычисляется
yn+1/2 = yn + b1k1 + b2k2
Теперь оценить погрешность можно по фомуле
εn(2) ≈ (1/c)·Dn -1 ·(yn+1 + yn+1/2)
где c — коэффициент, Dn -1 — матрица, обратная к матрице Dn .
В программе вычисляется коэффициент q2 из формулы
q2 3 ·║εn(2)║ = C·ε
где ε — заданная пользователем точность вычислений, C — коэффициент. Если q2 , то программа повторяет вычисления из прежней точки с меньшей величиной шага. Если q2 > 1 , то программа считает, что требуемая точность получена и переходит к вычислению следующего шага. В обоих случаях новый шаг расчитывается по формуле hnew = k·q2·hold , где k — понижающий коэффициент.
Норма ║ξ║ расчитывается по формуле
║ξ║ = max1≤j≤m<|ξj|/(|yn j | + r)>
где yn j — j-ая компонента решения, r – малый положительный параметр. Если |yn j | , применяется абсолютная погрешность, иначе относительная погрешность.
call DE53R(DSA, DSJA, X, Xout, H, Y, Eps, nWex, Error)
DSA, DSJA, Xout, nWex — входные параметры;
X, H, Y, Eps — выходные и выходные параметры;
Error — выходной параметр;
DSA(Y, DY) — процедура, которая вычисляет значения производных для автономной системы;
DSJA(Y, DYJ) — процедура, которая вычисляет значения матрицы Якоби для автономной системы. Частная производня от правой части i-го уравнения по j-ой переменной Y(i) запоминается в элементе DYJ(i,j) ;
Real X, Xout — начальная и конечная точки интегрирования, после удачного (не аварийного) завершения прграммы X = Xout ;
Real H — начальный шаг интегрирования, с которым программе предлагается начать вычисления. Допустимо задать абсолютное значение, даже если шаг должен быть отрицательным. На выходе переменная содержит величину шага в конце промежутка интегрирования;
Real Y(1:M) — массив, который на входе должен содержать начальные значения функций в точке X , на выходе будет содержать решение системы в точке Xout . Число M задает размерность решаемой системы уравнений;
Real Eps — требуемая точность интегрирования на каждом шаге. Так как алгоритм имеет 3-й порядок аппроксимации, оптимальным значением будет ε = 10 -4 ;
Integer nWex — задаёт режим вычисления Якобиана, может принимать значения 0 или 1; 0 — Якобиан вычисляется только один раз в начале программы; 1 — вычисляется на каждом шаге.
Integer Error — индикатор ошибки.
Error=0 , если интегрирование системы успешно закончено и решение вычислено с заданной точностью Eps на каждом шаге;
Error=1 , если интегрирование нельзя начать, т.к. значение |Xout-X| меньше минимально-допустимой величины шага hmin , которая вычисляется программой. Параметр H приобретает значение hmin ;
Error=2 , если интегрирование нельзя начать, т.к. заданное значение Eps меньше минимально-допустимой величины εmin , которая вычисляется программой. Параметр Eps приобретает значение εmin ;
Error=65 , если программа прекратила вычисления, т.к. решение не может быть вычислено с заданной точностью Eps . Переменная X получает значение аргумента, при котором произошло прекращение вычислений. Решение в точке X должно быть вычислено правильно.
В процессе вычислений программа DE53 вызывает программу AIG2R .
Программа DT10 решает краевую задачу для линейного дифференциального уравнения 2-го порядка y»(x) + q(x)y'(x) + p(x)y(x) = f(x) на промежутке [a, b] с граничными условиями y(a)=ya, y(b)=yb методом прогонки. Первая и вторая производные заменяются разностными схемами y’ = (yi+1 — yi-1)/2h и y» = (yi+1 — 2yi + yi-1)/h² , i = 1, . n-1; x0 = a , xn = b ; h = xi+1 — xi — шаг сетки. Подстановка прводит к системе из n-2 уравнений:
ai·yi-1 + bi·yi + ci·yi+1 = di, i = 1, . n-1
где ai = 2 — h·q(xi) , bi = -2(2 — h²·p(xi)) , ci = 2 + h·q(xi) , di = 2h²·f(xi) . Два недостающих уравнения беруться из граничных условий y(x0) = y0 и y(xn) = yn .
Получившаяся система из n уравнений с трёхдиагональной матрицей решается стандартным методом прогонки.
call DT10R(Q, P, F, A, B, YA, YB, X, Y)
Q, P, F, A, B, YA, YB — входные параметры;
X, Y — выходные параметры;
Real Q(x), P(x), F(x) — функции, определяющие дифференциальное уравнение;
Real A, B — граничные точки промежутка интегрирования;
Real YA, YB — значение фунуции в граничных точках;
Real X(1:n), Y(1:n) — массивы, которые по завершении работы программы содержат значения аргумента и функции. Число n задает разрядность сетки.
Программа DT11 решает краевую задачу для линейного дифференциального уравнения 2-го порядка y»(x) + q(x)y'(x) + p(x)y(x) = f(x) на промежутке [a, b] со смешанными граничными условиями методом прогонки. Первая и вторая производные заменяются разностными схемами y’ = (yi+1 — yi-1)/2h и y» = (yi+1 — 2yi + yi-1)/h² , i = 1, . n-1; x0 = a , xn = b ; h = xi+1 — xi — шаг сетки. Подстановка прводит к системе из n-2 уравнений:
ai·yi-1 + bi·yi + ci·yi+1 = di, i = 1, . n-1
где ai = 2 — h·q(xi) , bi = -2(2 — h²·p(xi)) , ci = 2 + h·q(xi) , di = 2h²·f(xi) . Два недостающих уравнения берём из смешанных граничных условий:
y'(x0) + α·y(x0) = α1
y'(xn) + β·y(xn) = β1
Данные граничные условия заменяем разностными схемами:
(1/2h)·(y1 — y-1) + α·y0 = α1
(1/2h)·(yn+1 — yn-1) + β·yn = β1
из которых выражаем неизвестные y-1 и yn+1 :
y-1 = y1 — 2h·(α1 — α·y0)
yn+1 = yn-1 + 2h·(β1 — β·yn)
Подставляем их в уравнения:
a0·y-1 + b0·y0 + c0·y1 = d0
an·yn-1 + bn·yn + cn·yn+1 = dn
и получаем два недостающих уравнения для решения системы:
(b0 + 2h·α·a0)·y0 + (a0 + c0)·y1 = d0 + 2h·α1·a0
(an + cn)·yn-1 + (bn — 2h·β·cn)·yn = dn — 2h·β1·cn
Получившаяся система из n уравнений с трёхдиагональной матрицей решается стандартным методом прогонки.
call DT11R(Q, P, F, A, B, Alpha, Alpha1, Beta, Beta1, X, Y)
Q, P, F, A, B, Alpha, Alpha1, Beta, Beta1 — входные параметры;
X, Y — выходные параметры;
Real Q(x), P(x), F(x) — функции, определяющие дифференциальное уравнение;
Real A, B — граничные точки промежутка интегрирования;
Real Alpha, Beta — коэффициент при функциях в граничных условиях;
Real Alpha1, Beta1 — правые части граничных условий;
Real X(1:n), Y(1:n) — массивы, которые по завершении работы программы содержат значения аргумента и функции. Число n задает разрядность сетки.
Численный метод штермера решения дифференциальных уравнений
Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,у’)=0 или у’=f(x,y). Функция y(x), при подстановке которой уравнение обращается в тождество, называется решением дифференциального уравнения.
Рассмотрим несколько численных методов решения дифференциальных уравнений первого порядка. Описание численных методов приводится для уравнения в виде у’=f(x,y).
Рассмотрим два варианта вывода расчетных формул
Численное решение математических моделей объектов заданных системами дифференциальных уравнений
Введение:
При математическом моделировании ряда технических устройств используются системы дифференциальных нелинейных уравнений. Такие модели используются не только в технике, они находят применение в экономике, химии, биологии, медицине, управлении.
Исследование функционирования таких устройств требуют решения указанных систем уравнений. Поскольку основная часть таких уравнений являются нелинейными и нестационарными, часто невозможно получить их аналитическое решение.
Возникает необходимость использовать численные методы, наиболее известным из которых является метод Рунге — Кутты [1]. Что касается Python, то в публикациях по численным методам, например [2,3], данных по применение Рунге — Кутты крайне мало, а по его модификации — методу Рунге-Кутта-Фельберга вообще нет.
В настоящее время, благодаря простому интерфейсу, наибольшее распространение в Python имеет функцию odeint из модуля scipy.integrate. Вторая функция ode из этого модуля реализует несколько методов, в том числе и упомянутый пятиранговый метод Рунге-Кутта-Фельберга, но, вследствие универсальности, имеет ограниченное быстродействие.
Целью настоящей публикации является сравнительный анализ перечисленных средств численного решения систем дифференциальных уравнений с модифицированным автором под Python методом Рунге-Кутта-Фельберга. В публикации так же приведены решения по краевым задачам для систем дифференциальных уравнений (СДУ).
Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
Для одного дифференциального уравнения n – го порядка, задача Коши состоит в нахождении функции, удовлетворяющей равенству:
и начальным условиям
Перед решением эта задача должна быть переписана в виде следующей СДУ
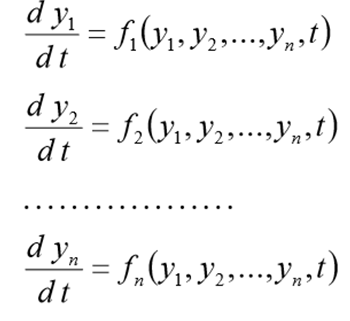
с начальными условиями
Модуль имеет две функции ode() и odeint(), предназначенные для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (задача Коши). Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.
Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат odeint(func, y0, t[,args=(), . ]) Аргумент func – это имя Python функции двух переменных, первой из которых является список y=[y1,y2. yn], а второй – имя независимой переменной.
Функция func должна возвращать список из n значений функций 
Второй аргумент y0 функции odeint() является массивом (или списком) начальных значений 
Третий аргумент является массивом моментов времени, в которые вы хотите получить решение задачи. При этом первый элемент этого массива рассматривается как t0.
Функция odeint() возвращает массив размера len(t) x len(y0). Функция odeint() имеет много опций, управляющих ее работой. Опции rtol (относительная погрешность) и atol (абсолютная погрешность) определяют погрешность вычислений ei для каждого значения yi по формуле
Они могут быть векторами или скалярами. По умолчанию
Вторая функция модуля scipy.integrate, которая предназначена для решения дифференциальных уравнений и систем, называется ode(). Она создает объект ОДУ (тип scipy.integrate._ode.ode). Имея ссылку на такой объект, для решения дифференциальных уравнений следует использовать его методы. Аналогично функции odeint(), функция ode(func) предполагает приведение задачи к системе дифференциальных уравнений вида (1) и использовании ее функции правых частей.
Отличие только в том, что функция правых частей func(t,y) первым аргументом принимает независимую переменную, а вторым – список значений искомых функций. Например, следующая последовательность инструкций создает объект ODE, представляющий задачу Коши.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
При численном решении задачи Коши
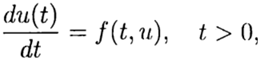

по известному решению в точке t =0 необходимо найти из уравнения (3) решение при других t. При численном решении задачи (2),(3) будем использовать равномерную, для простоты, сетку по переменной t с шагом т > 0.
Приближенное решение задачи (2), (3) в точке 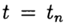

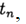


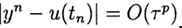

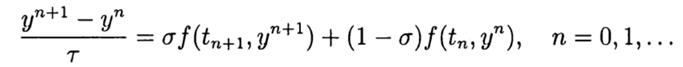
При 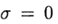
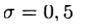
Явные схемы второго и более высокого порядка аппроксимации удобно строить, ориентируясь на метод предиктор-корректор. На этапе предиктора (предсказания) используется явная схема
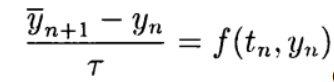
а на этапе корректора (уточнения) — схема
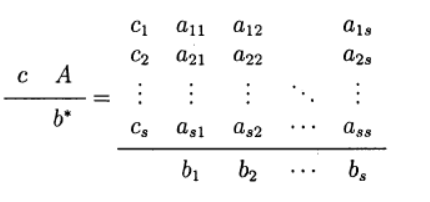
В одношаговых методах Рунге—Кутта идеи предиктора-корректора реализуются наиболее полно. Этот метод записывается в общем виде:

Формула (6) основана на s вычислениях функции f и называется s-стадийной. Если 
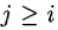

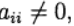

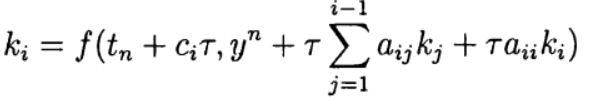
О таком методе Рунге—Кутта говорят как о диагонально-неявном. Параметры 
Одним из наиболее распространенных является явный метод Рунге—Кутта четвертого порядка

Метод Рунге—Кутта— Фельберга
Привожу значение расчётных коэффициентов 
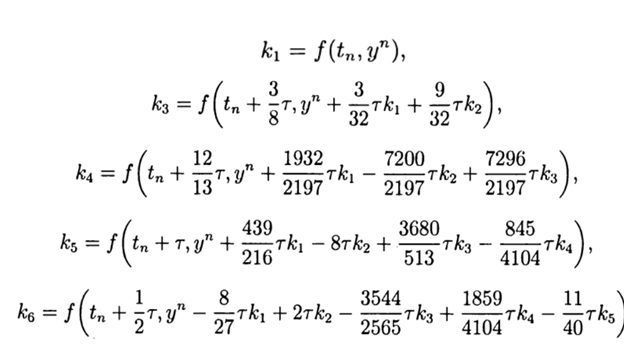
С учётом(9) общее решение имеет вид:
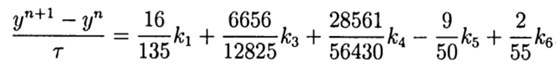
Это решение обеспечивает пятый порядок точности, остаётся его адаптировать к Python.
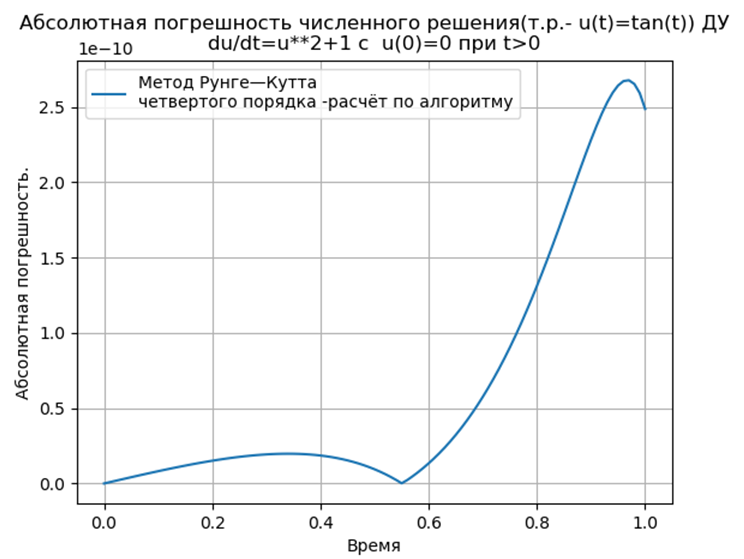
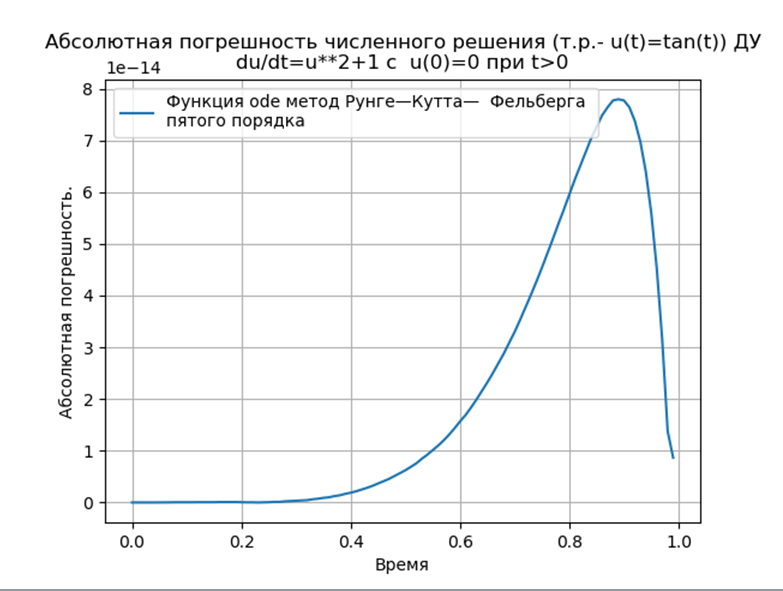
Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения  с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
Адаптированные к Python методы Рунге—Кутта и Рунге—Кутта— Фельберга имеют меньшую абсолютную, чем решение с применением функции odeint, но большую, чем с использованием функции edu. Необходимо провести исследование быстродействия.
Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
Сравнительный анализ проведём на примере модельной задачи, приведенной в [2]. Чтобы не повторять источник, приведу постановку и решение модельной задачи из [2].
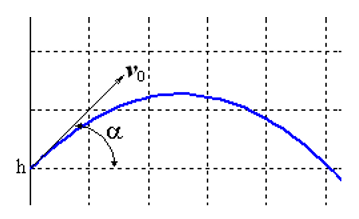
Решим задачу Коши, описывающую движение тела, брошенного с начальной скоростью v0 под углом α к горизонту в предположении, что сопротивление воздуха пропорционально квадрату скорости. В векторной форме уравнение движения имеет вид
где 



Особенность этой задачи состоит в том, что движение заканчивается в заранее неизвестный момент времени, когда тело падает на землю. Если обозначить 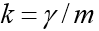
К системе следует добавить начальные условия: 

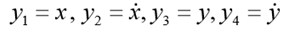
Для модельной задачи положим 
Flight time = 1.2316 Distance = 5.9829 Height =1.8542
Flight time = 1.1016 Distance = 4.3830 Height =1.5088
Flight time = 1.0197 Distance = 3.5265 Height =1.2912
Flight time = 0.9068 Distance = 2.5842 Height =1.0240
Время на модельную задачу: 0.454787
Для реализации средствами Python численного решения СДУ без использования специальных модулей, мною была предложена и исследована следующая функция:
def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6
Функция increment(f, t, y, tau) обеспечивает пятый порядок численного метода решения. Остальные особенности программы можно посмотреть в следующем листинге:
Время на модельную задачу: 0.259927
Предложенная программная реализация модельной задачи без использования специальных модулей имеет почти в двое большее быстродействие, чем с функцией ode, однако нельзя забывать, что ode имеет более высокую точность численного решения и возможности выбора метода решения.
Решение краевой задачи с поточно разделёнными краевыми условиями
Приведем пример некоторой конкретной краевой задачи с поточно разделенными краевыми условиями:
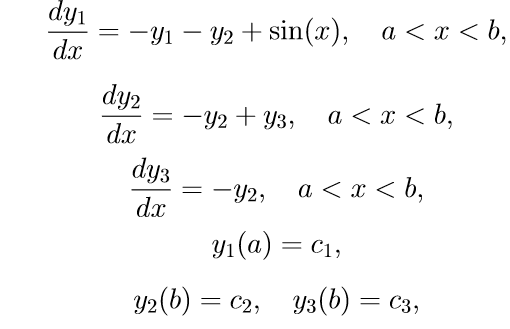
Для решения задачи (11) используем следующий алгоритм:
1. Решаем первые три неоднородные уравнения системы (11) с начальными условиями 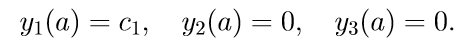
Введем обозначение для решения задачи Коши:
2. Решаем первые три однородные уравнения системы (11) с начальными условиями 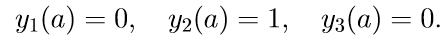
Введем обозначение для решения задачи Коши:
3. Решаем первые три однородные уравнения системы (11) с начальными условиями
Введем обозначение для решения задачи Коши:
4. Общее решение краевой задачи (11) при помощи решений задач Коши записывается в виде линейной комбинации решений: 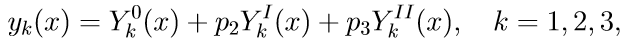
где p2, p3 — некоторые неизвестные параметры.
5. Для определения параметров p2, p3, используем краевые условия последних двух уравнений (11), то есть условия при x = b. Подставляя, получим систему линейных уравнений относительно неизвестных p2, p3:

Решая (12), получим соотношения для p2, p3.
По приведенному алгоритму с применением метода Рунге—Кутта—Фельберга получим следующую программу:
y0[0]= 0.0
y1[0]= 1.0
y2[0]= 0.7156448588231397
y3[0]= 1.324566562303714
y0[N-1]= 0.9900000000000007
y1[N-1]= 0.1747719838716767
y2[N-1]= 0.8
y3[N-1]= 0.5000000000000001
Время на модельную задачу: 0.070878
Вывод
Разработанная мною программа отличается от приведенной в [3] меньшей погрешностью, что подтверждает приведенный в начале статьи сравнительный анализ функции odeint с реализованным на Python метода Рунге—Кутта—Фельберга.
3. Н.М. Полякова, Е.В. Ширяева Python 3. Создание графического интерфейса пользователя (на примере решения методом пристрелки краевой задачи для линейных обыкновенных дифференциальных уравнений). Ростов-на-Дону 2017.
http://toehelp.ru/theory/informat/lecture13.html
http://habr.com/ru/post/418139/
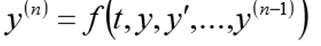
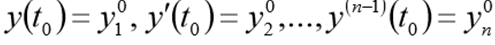


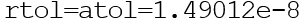
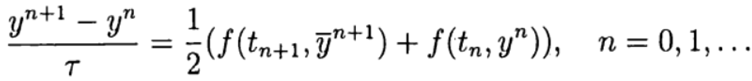
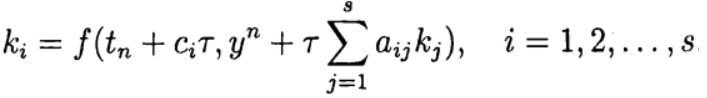
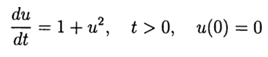 с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга