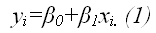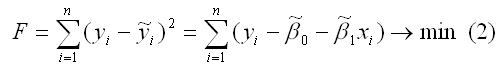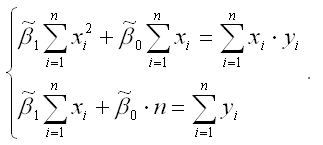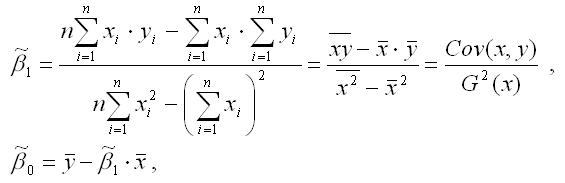Число нормальных уравнений равно числу

Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели парной регрессии

Предположим, что в ходе регрессионного анализа была установлена линейная взаимосвязь между исследуемыми переменными х и у, которая описывается моделью регрессии вида:

В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

Метод наименьших квадратов позволяет получить такие оценки параметров β₀и β₁, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) y˜ минимальна:

В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β₀ и β₁, потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции двух переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (2):

.

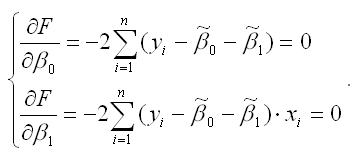
Если разделить обе части каждого уравнения системы на (-2), раскрыть скобки и привести подобные члены, то получим систему нормальных уравнений для функции регрессии вида yi=β₀+β₁xi:

Если решить данную систему нормальных уравнений, то мы получим искомые оценки неизвестных коэффициентов модели регрессии β₀ и β₁:

y – среднее значение зависимой переменной;

x – среднее значение независимой переменной;

xy – среднее арифметическое значение произведения зависимой и независимой переменных;

G 2 (x) – дисперсия независимой переменной;

Gcov (x, y) – ковариация между зависимой и независимой переменными.

Таким образом, явный вид решения системы нормальных уравнений может быть записан следующим образом:

30. Системы дифференциальных уравнений. Общие определения. Нормальные системы уравнений

ОпреДеление. Системой дифференциальных уравнений называется совокупность уравнений, в каждое из которых входят независимая переменная, искомые функции и их производНЫе.

Всегда предполагается, что число уравнений равно числу неизвестных функций.

Например, система двух дифференциальных уравнений первого порядка имеет вид

Наша задача состоит в том, чтобы найти функции и , удовлетворяющие обоим уравнениям. С системами дифференциальных уравнений мы сталкиваемся при изучении процессов, для описания которых одной функции недостаточно. Мы видели, что отыскание векторных линий поля приводит нас к системе дифференциальных уравнений. Ранее было отмечено, что изучение динамики криволинейного движения требует решения системы трех дифференциальных уравнений, в которых неизвестными функциями являются проекции движущейся точки на оси координат, а независимой переменной—время.

В настоящем параграфе будут рассмотрены некоторые простейшие системы дифференциальных уравнений.

Определение. Нормальной системой дифференциальных уравнений называется система уравнений вида

(*)

Решением такой системы называется совокупность П функций удовлетворяющих всем уравнениям системы.

Частным решением системы (*) называется решение, удовлетворяющее заданным начальным условиям

Где — Заданные постоянные величины.

Покажем, не приводя доказательства, что, как правило, данную систему дифференциальных уравнений можно привести к нормальной, ей эквивалентной.

1. Приведем к нормальной систему линейных уравнений

Разрешив данные уравнения относительно производных и :

Мы и получаем нормальную систему.

2. Систему уравнений

Нельзя разрешить относительно и . Следовательно, эту систему нельзя привести к нормальной. Подобные системы мы Рассматривать не будем.

3. Приведем к нормальной систему уравнений

Здесь для приведения системы к нормальной мы введем вспомогательные функции и . Тогда , И заданная система заменится следующей:

Полученная система уже является нормальной.

Покажем теперь, что одно дифференциальное уравнение N-го порядка, разрешенное относительно старшей производной, с помощью введения новых вспомогательных функций всегда можно свести к нормальной системе дифференциальных уравнений.

Возьмем, например, уравнение третьего порядка

И введем две новые вспомогательные функции

Тогда заданное уравнение заменится системой трех уравнений

Которая является частным случаем нормальной системы (*). Ясно, что так можно поступать в случае уравнения любого порядка П; При этом число вспомогательных функций будет равно N-1.

В обычно встречающихся случаях верно и обратное утверждение:

Нормальная система уравнений может быть заменена однИМ дифференциальным уравнением, порядок которого равен числУ Уравнений системы.

Рассмотрим, например, систему уравнений

Продифференцируем первое уравнение по переменной T и ЗАменим производную ее выражением из второго уравнения:

Продифференцируем еще раз это уравнение и заменим производную ее выражением из третьего уравнения:

Так как , А , то окончательно получим:

Т. Е. линейное дифференциальное уравнение третьего порядка с постоянными коэффициентами.

Обращаем внимание читателя, что в процессе исключения функций У и Z мы выражаем их через функцию Х и ее производные. Найдя общее решение полученного дифференциального уравнения высшего порядка, мы получим выражение для функции Х, зависящее от трех произвольных постоянных. Остальные неизвестные функции (У и Z) находятся уже не при помощи интегрирования, а из их выражений через найденную функцию. Таким образом, общее число произвольных постоянных не увеличится и будет равно порядку системы. Решим полученное уравнение третьего порядка

Характеристическое уравнение, ему соответствующее: , имеет корни Следовательно,

Поскольку при исключении У и Z мы получали и , то

На основании рассмотренного примера МЫ сделаем следующий вывод (доказательство его мы опускаем):

Общее решение нормальной системы

(*)

Где — произвольные постоянные.

Задаваясь начальными условиями, мы получаем П уравнений для определения этих произвольных постоянных:

(**)

Для нормальных систем уравнений также имеет место теорема, гарантирующая существование и единственность частного решения.

Теорема. Если правые части нормальной системы непрерывны вместе со своими частными производными при значениях , то существует единственная система функций , являющаяся решением системы и удовлетворяющая заданным начальным условиям.

Число нормальных уравнений равно числу

Параметры уравнений регрессии находят решением системы нормальных уравнений, отвечающих требованию способа наименьших квадратов. [c.390]

Величины указанных параметров были рассчитаны решением системы нормальных уравнений, получаемых способом наименьших квадратов [c.24]

Это условие приводит к системе нормальных уравнений, решение которых позволяет определить параметры уравнения регрессии. Эти уравнения имеют вид [c.99]

Считая формулу связи линейной (Y = a0 + aiX ), определяем зависимость рентабельности производства плащей в зависимости от рентабельности выпуска зонтов. Для этого решается система нормальных уравнений [c.83]

Этап 3. Система нормальных уравнений для функции имеет вид [c.223]

Считая формулу связи линейной (у = а0 + щх), определим зависимость выпуска промышленных изделий от их запуска. Для этого решается система нормальных уравнений [c.160]

Для исчисления параметров я0 и я, используется система нормальных уравнений [c.368]

В случае выравнивания по прямой способ наименьших квадратов приводит к следующей системе нормальных уравнений [c.322]

По такому же принципу рассчитываются и параметры криволинейного уравнения. Так, в случае параболической зависимости параметры а0, аь а2 находятся по следующей системе нормальных уравнений [c.322]

Вторым этапом является поиск значений параметров уравнения. Параметры трендовых моделей определяются с помощью системы нормальных уравнений. В случае применения линейного тренда используют следующую систему уравнений, которую решают способом наименьших квадратов [c.612]

Величина k определяет гармонику ряда Фурье и определяется целым числом, как правило, в пределах от 1 до 4. Параметры уравнения находят с помощью системы нормальных уравнений способом наименьших квадратов. [c.616]

Отсюда система нормальных уравнений имеет вид [c.239]

Коэффициенты регрессии для представления (4.16) находятся с помощью системы нормальных уравнений (чтобы не загромождать запись, индекс k, по которому идет суммирование у результативного и факторных признаков, подразумевается, но не приводится k — 1,2,. . п). [c.125]

Параметры уравнения OQ, а и а находим из системы нормальных уравнений, при ] / = 0 значения параметров рассчитываются по формулам [c.185]

Значения констант а0, а,, а2,. .. могут быть вычислены путем решения системы нормальных уравнений. [c.126]

Анализ зависимости между ценой продукта и его количеством в динамике позволяет выбрать для функции спроса линейную форму связи вида Р= а0 + а[ + a(Q. По методу наименьших квадратов определяются неизвестные параметры ай и а[ на основе составления и решения системы нормальных уравнений вида [c.74]

Анализ зависимости между издержками и количеством выпускаемой продукции в динамике позволяет для функции издержек выбрать также линейную форму связи вида С= Ь0 + b Q. Неизвестные параметры Ь0 и Ь( также находятся по методу наименьших квадратов на основе составления и решения системы нормальных уравнений вида [c.75]

Уравнение прямой имеет вид у, = а0 + а t. В связи с этим система нормальных уравнений для оценивания параметров прямой имеет вид [c.81]

Упрощенный расчет параметров уравнений заключается в переносе начала координат в середину ряда динамики. В этом случае упрощаются сами нормальные уравнения, а кроме того, уменьшаются абсолютные значения величин, участвующих в расчете. В самом деле, если до переноса начала координат / было равно 1,2,3,. . п, то после переноса — t=. .. —4, — 3, —2, -1,0,1,2,3,4. если число члена ряда нечетное. Когда же число ряда четное, то f =. —5, —3, — 1, 1,3,5. Следовательно, /и все f, у которых р нечетное число, равны 0. Таким образом, все члены уравнений, содержащие /с такими степенями, могут быть исключены. Системы нормальных уравнений теперь упрощаются для прямой [c.82]

Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид [c.115]

В данном случае задача сводится к определению неизвестных параметров а0 а а2. Они определяются на основе системы нормальных уравнений [c.115]

А, а, р и у — параметры производственной функции, которые определяются в результате решения системы нормальных уравнений. [c.363]

При функциональной форме мультиколлинеарности по крайней мере одна из парных связей между объясняющими переменными является линейной функциональной зависимостью. В этом случае матрица Х Х особенная, так как содержит линейно зависимые векторы-столбцы и ее определитель равен нулю, т. е. нарушается предпосылка 6 регрессионного анализа. Это приводит к невозможности решения соответствующей системы нормальных уравнений и получения оценок параметров регрессионной модели. [c.108]

Система нормальных уравнений 54 ——в матричной форме 85 [c.304]

Определение зависимости изменения затрат от изменения технико-экономических параметров изделий включает следующие основные этапы объединение изделий в параметрические ряды отбор параметров, в наибольшей степени влияющих на себестоимость изделий установление формы связи зависимости изменения себестоимости от изменения параметров построение системы нормальных уравнений в соответствии с принятой функцией и расчет коэффициентов. [c.185]

Система нормальных уравнений будет выглядеть следующим образом [c.158]

По данным, приведенным в табл. 5.7 (итоги гр. 2-6), построена система нормальных уравнений [c.204]

Полученная система называется системой нормальных уравнений для нахождения параметров а0 и ах при выравнивании по прямой линии. — [c.47]

Для получения конкретного математического выражения функциональной связи между двумя переменными у» is. х при гиперболической их взаимозависимости составлена система нормальных уравнений [c.52]

Из системы нормальных уравнений находим параметры b и а [c.29]

Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии [c.49]

Система нормальных уравнений составит [c.115]

Для определения параметров а и Ь применяется МНК. Система нормальных уравнений следующая [c.146]

Система нормальных уравнений будет иметь вид [c.45]

Применение МНК для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений [c.63]

Напомним, что в математической статистике для получения несмещенной оценки дисперсии случайной величины соответствующую сумму квадратов отклонений от средней делят не на число наблюдений я, а на число степеней свободы (degress of freedom) я — т, равное разности между числом независимых наблюдений случайной величины п и числом связей, ограничивающих свободу их изменения, т. е. число т уравнений, связывающих эти наблюдения. Поэтому в знаменателе выражения (3.26) стоит число степеней свободы п — 2, так как две степени свободы теряются при определении двух параметров прямой из системы нормальных уравнений (3.5). [c.62]

Напомним, что согласно методу наименьших квадратов параметры прямой1 у, = /(0 = Ь0 + bit находятся из системы нормальных уравнений (3.5), в которой в качестве х, берем t [c.141]

При применении метода наименьших квадратов для оценки параметров экспоненциальной, логистической функций или функции Гомперца возникают сложности с решением получаемой системы нормальных уравнений, поэтому предварительно, до получения соответствующей системы, прибегают к некоторым преобразованиям этих функций (например, логарифмированию и др.) (см. 5.5). [c.143]

В этом модуле реализовано решение системы нормальных уравнений методом наименьших квадратов. Прогноз с использованием модуля М107 осуществляется на базе небольшого числа данных (N > 10) по упрощенной схеме, т. е. по трем наиболее распространенным функциям [c.41]

На основе коэффициентов парной корреляции обра зуется система нормальных уравнений, однако, относящаяся ие к. самим коэффициентам уравнения О , а к таким же величинам в стандартизованном масштабе р [c.45]