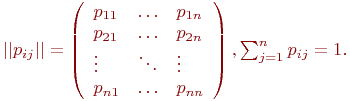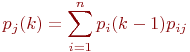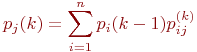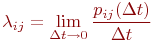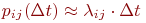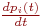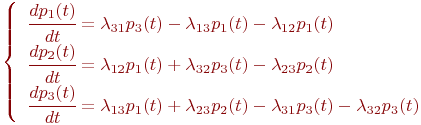Компьютерное моделирование — тест 2
Упражнение 1: Номер 1
Ответ:
Упражнение 2: Номер 1
Ответ:
Упражнение 3: Номер 1
Ответ:
Упражнение 4: Номер 1
Ответ:
Упражнение 5: Номер 1
Ответ:
Упражнение 6: Номер 1
Ответ:
Упражнение 7: Номер 1
Ответ:
Упражнение 8: Номер 1
Ответ:
Упражнение 9: Номер 1
Ответ:
Упражнение 10: Номер 1
Ответ:
Упражнение 11: Номер 1
Ответ:
Упражнение 12: Номер 1
Ответ:
Упражнение 13: Номер 1
Ответ:
Упражнение 14: Номер 1
Ответ:
Упражнение 15: Номер 1
Ответ:
Конспект лекций по дисциплине «Моделирование и анализ бизнес-процессов» (стр. 2 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 |
Однако система уравнений (1) является вырожденной, и для нахождения единственного решения в этой системе одно любое уравнение нужно заменить на условие нормировки

Пример 2. Автоматизированная сборочная линия предприятия в среднем 1 раз в месяц выходит из строя и ремонтируется в среднем 3 дня. Кроме того, в среднем 2 раза в месяц она проходит техническое обслуживание, которое длится в среднем 1 день.
В среднем в одном случае из трех при техническом обслуживании обнаруживается неполадка, и линия ремонтируется. Определить, какую среднюю прибыль приносит линия за месяц, если за один день безотказной работы прибыль равна 15 тыс. р. Один день технической обработки обходится в 20 тыс. р., а один день ремонта — 30 тыс. р.
Решение. Найдем вероятности состояний, равные долям времени работы, ремонта и технического обслуживания. Пусть:
S1 — линия работает;
S2 — техническое обслуживание;
Граф состояний будет иметь вид:
Составляем систему уравнений. В состояние S1 входят 2 стрелки: из S2 с интенсивностью 20 и из S3 с интенсивностью 10, поэтому левая часть первого уравнения имеет вид 

Однако данная система является вырожденной, и для ее решения нужно заменить одно любое (например, первое) уравнение условием нормировки 
Выражаем из 1-го и 2-го уравнений Р1 и Р3 через Р2: 



Пример 3. В туристическом агентстве работает продавец и менеджер. В среднем в агентство приходят 2 клиента за час. Если продавец свободен, он обслуживает клиента, если – занят, то клиента обслуживает менеджер, если оба заняты — клиент уходит. Среднее время обслуживания продавцом 20 минут, менеджером — 30 минут. Каждый клиент приносит среднюю прибыль 100 рублей.
Определить среднюю прибыль агентства за 1 час и среднее число упущенных клиентов за час.
Решение. Определяем состояния системы:
S1 — продавец и менеджер свободны;
S2 — продавец занят, менеджер свободен;
S3 — продавец свободен, менеджер занят;
Строим граф состояний
Составляем систему уравнений, заменяя 4-е уравнение условием нормировки:
Решая систему уравнений, находим:

Следовательно, продавец занимается обслуживанием P2 + P4 = 0,25 + 0,15 = 0,4, то есть 40 % времени. Если бы он обслуживал 100 % времени, то за час обслуживал бы 3-х клиентов, а реально: 3 Ч 0,4 = 1,2 и приносит прибыль за 1 час 120 рублей. Менеджер работает P3 + P4 = 0,11 + 0,15 = 0,26, т. е. 26 % времени и поэтому за час обслужит 2 Ч 0,26 = 0,52 клиента и принесет прибыль 52 рубля в час. Средняя прибыль за 1 час составит 172 рубля. Клиенты теряются в состоянии S4. Так как P4 = 0,15, то в час теряется 15 % клиентов из 2-х возможных или 0,3 клиента. Убытки составляют
30 рублей в час из-за потерянных клиентов.
4. Процессы гибели и размножения
Во многих экономических системах, в которых функционирует СП, возникают ситуации, когда из любого (кроме первого и последнего) состояния Si возможен переход только в соседние состояния Si+1 и Si-1. Такие процессы называются процессами гибели и размножения, и они описываются графом состояний
Интенсивности 




Пример 4. В автохозяйстве 5 автомобилей. Каждый из них в среднем 4 раза в год ломается, и ремонт длится в среднем
1 месяц. Определить, какую долю времени все автомобили исправны и среднее число исправных автомобилей в произвольный момент времени.
Решение. Вводим состояния системы:
S0 — все автомобили сломаны;
S1 — 1 автомобиль исправен;
S2 — 2 автомобиля исправны;
S3 — 3 автомобиля исправны;
S4 — 4 автомобиля исправны;
S5 — 5 автомобилей исправны.
Построим граф состояний и расставим переходные интенсивности. Например, для перехода из S1 в S0 имеем ситуацию: исправен 1 автомобиль, и он ломается,— это происходит 4 раза в год, т. е. интенсивность равна 4. Для перехода из S2 в S1: исправны 2 автомобиля и каждый из них ломается 4 раза в год, т. е. интенсивность равна 8. Остальные интенсивности гибели расставляются по аналогии.
Для перехода из S4 в S5 имеем ситуацию: неисправен 1 автомобиль, и он ремонтируется, — это длится 1 месяц или 12 раз в год, т. е. интенсивность равна 12. Для перехода из S3 в S4 имеем ситуацию: неисправны 2 автомобиля и каждый из них может быть отремонтирован с интенсивностью 12, т. е. общая интенсивность равна 24. Остальные интенсивности размножения расставляются по аналогии.
Вычисляем вероятности состояний, равные средней доле времени нахождения системы в этих состояниях.





Все автомобили исправны в состоянии S5, средняя доля времени, когда автомобили исправны – 0,24. Среднее число исправных автомобилей находится как математическое ожидание:

Пример 5. Организация принимает заявки от населения на проведение ремонтных работ. Заявки принимаются по телефону по двум линиям, и их обслуживают два диспетчера. Если одна линия занята, заявка автоматически переключается на вторую. Если обе линии заняты — заявка теряется. Среднее число обслуживания одной заявки — 6 минут. В среднем одна заявка приносит прибыль в 30 рублей. Какова прибыль за час? Целесообразно ли организовывать третий канал с третьим диспетчером, если его обслуживание обойдется в 150 рублей в час?
Решение. Рассмотрим сначала систему с двумя каналами.
Введем возможные состояния:
S0 — нет заявок (оба телефона свободны);
S1 — одна заявка обслуживается (один телефон занят);
S2 — две заявки обслуживаются (оба телефона заняты).
Граф состояний будет иметь вид
Применяя формулы для расчета вероятностей состояний, имеем:
В среднем за час теряется 54 % заявок или 0,54 Ч 30 = 16,2 заявки. Обслуживается 13,8 заявок в час и средняя прибыль 13,8 Ч 30 =
= 414 рублей.
Рассмотрим ситуацию с тремя линиями. Граф состояний при этом будет иметь вид
Находим вероятности состояний:

В среднем теряется 35 % заявок или 10,4 заявки в час. Обслуживается 19,6 заявок. Средняя прибыль — 588 рублей в час. Прибыль выросла на 174 р. При затратах 150 рублей третий канал обслуживания вводить целесообразно.
Марковские случайные процессы. Уравнения Колмогорова для вероятностей состояний.
Наиболее полное исследование процесса функционирования систем получается, если известны явные математические зависимости, связывающие искомые показатели с начальными условиями, параметрами и переменными исследуемой системы. Для многих современных систем, являющихся объектами моделирования, такие математические зависимости отсутствуют или малопригодны, и следует применять другое моделирование, как правило, имитационное.
Большой класс случайных процессов составляют процессы без последействия, которые в математике называют марковскими процессами в честь Андрея Андреевича Маркова — старшего (1856 — 1922), выдающегося русского математика, разработавшего основы теории таких процессов.
Случайный процесс называется марковским, если вероятность перехода системы в новое состояние зависит только от состояния системы в настоящий момент и не зависит от того, когда и каким образом система перешла в это состояние.
Практически любой случайный процесс является марковским или может быть сведен к марковскому. В последнем случае достаточно в понятие состояния включить всю предысторию смен состояний системы.
Марковские процессы делятся на два класса:
· дискретные марковские процессы (марковские цепи);
· непрерывные марковские процессы.
Дискретной марковской цепьюназывается случайный процесс, при котором смена дискретных состояний происходит в определенные моменты времени.
Непрерывным марковским процессомназывается случайный процесс, при котором смена дискретных состояний происходит в случайные моменты времени.
Рассмотрим ситуацию, когда моделируемый процесс обладает следующими особенностями.
Система 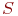
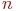
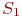
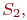
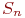
Смена состояний происходит, будем считать, мгновенно и в строго определенные моменты времени 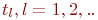
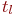
Известны вероятности перехода 

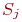
Цель моделирования: определить вероятности состояний системы после 
Обозначим эти вероятности 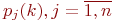

Если в системе отсутствует последействие, то есть вероятности 

Марковская цепь называется однородной, если переходные вероятности 
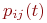
Значения 
Значения 
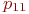
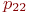
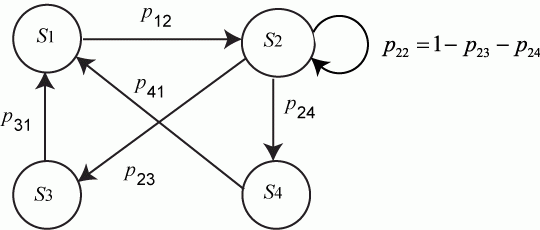
Не указываются также нулевые вероятности переходов. Например, на рис. это вероятности 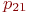
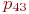
Математической моделью нахождения вероятностей состояний однородной марковской цепи является рекуррентная зависимость
где 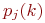
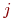

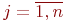
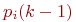
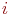

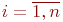

Рис.Размеченный граф состояний системы
Для неоднородной марковской цепи вероятности состояний системы находятся по формуле:
где 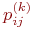

Сформулируем методику моделирования по схеме дискретных марковских процессов (марковских цепей).
1. Зафиксировать исследуемое свойство системы.
Определение свойства зависит от цели исследования. Например, если исследуется объект с целью получения характеристик надежности, то в качестве свойства следует выбрать исправность. Если исследуется загрузка системы, то — занятость. Если состояния объектов, то — поражен или непоражен.
2. Определить конечное число возможных состояний системы и убедиться в правомерности моделирования по схеме дискретных марковских процессов.
3. Составить и разметить граф состояний.
4. Определить начальное состояние.
5. По рекуррентной зависимости определить искомые вероятности.
В рамках изложенной методики моделирования исчерпывающей характеристикой поведения системы является совокупность вероятностей 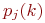
При моделировании состояния систем с непрерывными марковскими процессами мы уже не можем воспользоваться переходными вероятностями 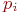

Поэтому вместо переходных вероятностей вводятся в рассмотрение плотности вероятностей переходов 
где 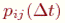


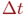
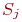
С точностью до бесконечно малых второго порядка из приведенной формулы можно представить:
Непрерывный марковский процесс называется однородным,если плотности вероятностей переходов 

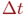
Целью моделирования,как и в случае дискретных процессов, является определение вероятностей состояний системы 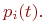
Сформулируем методику моделирования по схеме непрерывных марковских процессов.
1. Определить состояния системы и плотности вероятностей переходов 
2. Составить и разметить граф состояний.
3. Составить систему дифференциальных уравнений Колмогорова. Число уравнений в системе равно числу состояний. Каждое уравнение формируется следующим образом.
4. B левой части уравнения записывается производная вероятности 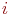
5. В правой части записывается алгебраическая сумма произведений 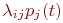
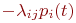
6. Определить начальные условия и решить систему дифференциальных уравнений.
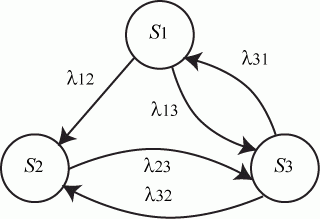
Пример. Составить систему дифференциальных уравнений Колмогорова для нахождения вероятностей состояний системы, размеченный граф состояний которой представлен на рисунке.
Рис. Размеченный граф состояний
Очевидно, 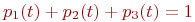
Поэтому любое из первых трех уравнений можно исключить, как линейно зависимое.
Для решения уравнений Колмогорова необходимо задать начальные условия. Для рассмотренного примера можно задать такие начальные условия: 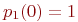
Дата добавления: 2015-04-03 ; просмотров: 7881 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://pandia.ru/text/80/457/74164-2.php
http://helpiks.org/3-4019.html