Уравнение колебаний маятника
Рис.1
Исследуем выражение (2) в зависимости от разности фаз (φ2 — φ1):
1) φ2 — φ1 = ±2mπ (m = 0, 1, 2, . ), тогда A=A1+A2, т. е. амплитуда результирующего колебания А будет равна сумме амплитуд складываемых колебаний;
2) φ2 — φ1 = ±(2m+1)π (m = 0, 1, 2, . ), тогда A=|A1–A2|, т. е. амплитуда результирующего колебания будет равна разности амплитуд складываемых колебаний.
Для практики представляет особый интерес случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. После сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, которые возникают при сложении двух гармонических колебаний с близкими частотами, называются биениями.
Пусть амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω
23 Колебания физического маятника.
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Определения
— угол отклонения маятника от равновесия;
— начальный угол отклонения маятника;
— масса маятника;
— расстояние от точки подвеса до центра тяжести маятника;
— радиус инерции относительно оси, проходящей через центр тяжести.
— ускорение свободного падения.
Момент инерции относительно оси, проходящей через точку подвеса:

[править] Дифференциальное уравнение движения физического маятника
Основная статья: Приведённая длина
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:
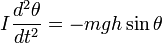
Полагая 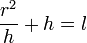
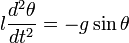
Последнее уравнение аналогично уравнению колебаний математического маятника длиной 

[править] Центр качания физического маятника
Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.
Поместим на луче, проходящем от точки подвеса через центр тяжести точку на расстоянии 
Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром масс. Тогда момент инерции относительно оси подвеса будет равен 
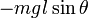
[править] Теорема Гюйгенса
[править] Формулировка
Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.
[править] Доказательство
Вычислим приведенную длину для нового маятника:
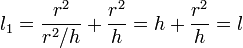
Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.
[править] Период колебаний физического маятника
Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания. Для этого умножим левую часть этого уравнения на 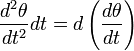
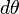
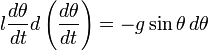
Интегрируя это уравнение, получаем.
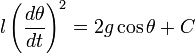
где 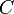
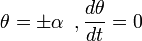
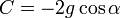
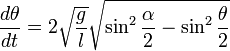
Отделяем переменные и интегрируем это уравнение:
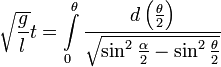
Удобно сделать замену переменной, полагая 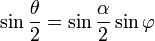
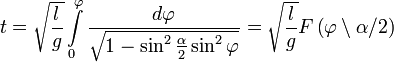
Здесь 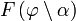
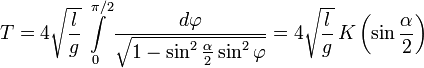
Здесь 
[править] Период малых колебаний физического маятника
Если амплитуда колебаний 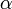
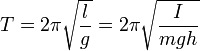
24 Колебания математического маятника
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины l неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит [1] от амплитуды и массы маятника.
Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.
При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.
Уравнение колебаний маятника
Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида
где ω ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция x(t) ― это угол отклонения маятника в момент t от нижнего положения равновесия, выраженный в радианах; 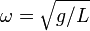
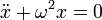
[править] Решения уравнения движения
[править] Гармонические колебания
Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:
где A — амплитуда колебаний маятника, θ0 — начальная фаза колебаний, ω — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями
[править] Нелинейный маятник
Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:
где 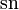

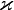
Параметр 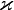
где 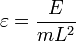
Период колебаний нелинейного маятника
где K — эллиптический интеграл первого рода.
[править] Движение по сепаратрисе
Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, и останавливается, возвратившись в исходное положение.
25 Затухающие колебания. Зависимость амплитуды от времени.
Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида 
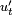
Пускай имеется система, состоящая из пружины (подчиняющейся закону Гука), один конец которой жёстко закреплён, а на другом находится тело массой m. Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c (см. вязкое трение).
Тогда второй закон Ньютона для рассматриваемой системы запишется так:
где Fc — сила сопротивления, Fy — сила упругости
или в дифференциальной форме
где k — коэффициент упругости в законе Гука, c — коэффициент сопротивления, устанавливающий соотношение между скоростью движения грузика и возникающей при этом силой сопротивления.
Для упрощения вводятся следующие обозначения:
Величину ω называют собственной частотой системы, ζ — коэффициентом затухания.
Тогда дифференциальное уравнение принимает вид
Сделав замену x = e λt , получают характеристическое уравнение
Корни которого вычисляются по следующей формуле
[править] Решения
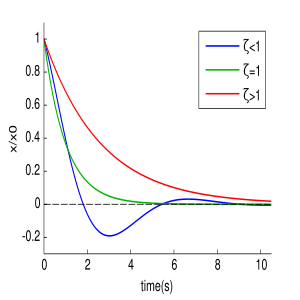
Зависимость графиков колебаний от значения ζ.
В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта.
Если 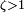
В этом случае колебания с самого начала экспоненциально затухают.
- Граница апериодичности
Если 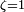
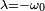
В данном случае может иметь место вре́менный рост, но потом — экспоненциальное затухание.
Если 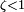
Тогда решением исходного дифференциального уравнения является
Где 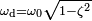
Константы c1 и c2 в каждом из случаев определяются из начальных условий:
26 Вынужденные колебания. Понятие резонанса.
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону: 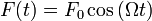
Что будет решением дифференциального уравнения физического маятника
Определите дифференциальное уравнение физического маятника:
Савельев И.В, т.1, стр. 196
В случае малых колебаний (54.8) переходит в уже известное нам уравнение:

Трофимова Т.И. Курс физики, 2001 г., стр. 202

идентичное с (142.1), решение которого (140.1) известно.
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:

Полагая 

Последнее уравнение аналогично уравнению колебаний математического маятника длиной 

Вывод дифференциального уравнения колебаний физического маятника
6.11. Физический маятник
Твердое тело произвольной формы, свободно совершающее колебания вокруг неподвижной горизонтальной оси, не проходящей через его центр масс, называют физическим маятником .
Согласно определению, физический маятник при колебаниях имеет одну степень свободы, т.е. действительно является одномерным гармоническим классическим осциллятором (рис. 6.14, где точка 0 называется осью качаний, а точка 0 * — центром качания физического маятника, точка C — центр масс).
При гармонических колебаниях угол отклонения от положения равновесия q мал и составляет не более трех-пяти градусов, что позволяет в некоторых случаях полагать sin q » q (если угол q брать в радианах, а не в градусах), а сами колебания считать гармоническими и изохронными , т.е. их период или частота не зависят от амплитуды колебания.
Сначала напишем дифференциальное уравнение колебаний физического маятника. Для этого рассмотрим, какие на него действуют силы. Силу трения в точке подвеса 0 (ось Z ) физического маятника не учитываем. На физический маятник при колебаниях действуют сила тяжести G и нормальная реакция опоры F (рис. 6.14). Для нахождения результирующей силы разложим силу тяжести на две взаимно перпендикулярные силы: G ^ = mg · sin q и G | | = mg · cos q (рис. 6.14). Тогда силы нормальной реакции опоры и параллельная составляющая силы тяжести взаимно компенсируют друг друга (третий закон Ньютона). Поэтому силой, заставляющей физический маятник продолжать совершать гармонические колебания, остается перпендикулярная составляющая силы тяжести, которую часто называют возвращающей силой.
Такой же результат можно получить, если сложить вектор силы тяжести и вектор силы нормальной реакции опоры по правилу параллелограмма. (Представляем читателю выполнить эту операцию самостоятельно).
Из динамики вращательного движения ( 5.17 ) следует , что в этом случае на физический маятник (как любое твердое тело) действует момент силы М относительно оси Z, равный произведению момента инерции тела I на угловое ускорение e относительно этой же оси:
| M = I ×e , |
 . . |
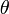 — угол отклонения маятника от равновесия;
— угол отклонения маятника от равновесия; — масса маятника;
— масса маятника;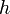 — расстояние от точки подвеса до центра тяжести маятника;
— расстояние от точки подвеса до центра тяжести маятника; — радиус инерции относительно оси, проходящей через центр тяжести.
— радиус инерции относительно оси, проходящей через центр тяжести.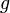 — ускорение свободного падения.
— ускорение свободного падения.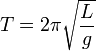

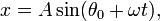
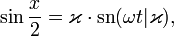
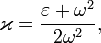


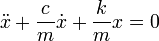
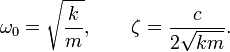
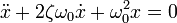

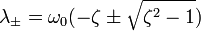

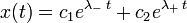

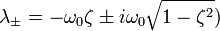
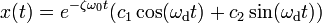
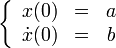



 , (4.18)
, (4.18) ,
, . (4.19)
. (4.19) . (4.20)
. (4.20) , то придём к уравнению
, то придём к уравнению , (4.21)
, (4.21) Физическим маятником называют колебания твёрдого тела под действием силы тяжести вокруг горизонтальной оси, не проходящей через центр масс тела (точку С на рис. 4.6). Отведём маятник из положения равновесия на некоторый малый угол α. Запишем теперь 2-й закона Ньютона для вращательного движения
Физическим маятником называют колебания твёрдого тела под действием силы тяжести вокруг горизонтальной оси, не проходящей через центр масс тела (точку С на рис. 4.6). Отведём маятник из положения равновесия на некоторый малый угол α. Запишем теперь 2-й закона Ньютона для вращательного движения . (4.22)
. (4.22) . (4.23)
. (4.23) . (4.24)
. (4.24) и окончательно получим
и окончательно получим . (4.25)
. (4.25) . (4.26)
. (4.26) и периодом
и периодом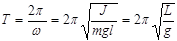 , (4.27)
, (4.27) называется приведенной длиной физического маятника. Точка O’, которая находится на расстоянии приведенной длины от точки подвеса, называется центром качаний физического маятника. Точка подвеса маятника О и центр качаний обладают свойством взаимности – если маятник перевернуть и подвесить за точку O’, то период колебания маятника не изменится.
называется приведенной длиной физического маятника. Точка O’, которая находится на расстоянии приведенной длины от точки подвеса, называется центром качаний физического маятника. Точка подвеса маятника О и центр качаний обладают свойством взаимности – если маятник перевернуть и подвесить за точку O’, то период колебания маятника не изменится. . (4.29)
. (4.29) | 7530 —
| 7530 —  или читать все.
или читать все.