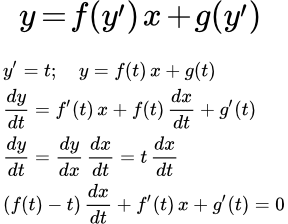Что мы находим из уравнения лагранжа

Дифференциальное уравнение Лагранжа

Решение дифференциального уравнения Лагранжа

Рассмотрим дифференциальное уравнение Лагранжа:
(1) ,
где и – это функции.
Будем искать его решение в параметрическом виде. То есть будем считать, что , , а также производная являются функциями от параметра . Положим
.
Поставим в (1):
(2) .
Продифференцируем по :
(3) .
С другой стороны:
(4) .
Левые части уравнений (3) и (4) равны. Приравниваем правые части и выполняем преобразования:
;
.

Разделим на . При уравнение принимает вид:
.
Это линейное дифференциальное уравнение относительно переменной . Решая его, получаем зависимость переменной от параметра : . Затем подставляем в (2):
.
В результате получаем зависимость переменной от параметра : . То есть мы получили параметрическое представление решения уравнения (1).

Дополнительные решения дифференциального уравнения Лагранжа

В процессе приведения уравнения к линейному, мы разделили уравнение на . Поэтому мы рассматривали решение при . В заключении следует рассмотреть случай , то есть исключить параметр из уравнений:
(5) ;
(6) .

Уравнение (5) содержит только переменную t . Поэтому его нужно решить и определить корни. Если корней нет, то дополнительных решений также нет.

Предположим, что мы нашли корни уравнения (5) (один или несколько). Обозначим такой корень как :
(7) .
Тогда уравнение (6) дает нам зависимость y от x , которая является линейной функцией:
.
Поскольку в силу (7), , то
(8) .

Покажем, что (8) является решением исходного уравнения (1). Для этого найдем производную (8). Она равна постоянной:
.
Подставим (8) и в (1):
;
;
.
Это уравнение выполняется, поскольку в силу (7), .

Таким образом, мы нашли, что уравнение (1) может иметь решения
,
где – корни уравнения
.

Пример

Решить уравнение:
(1.1)

Разделим на . При имеем:
(1.2) .
Это уравнение Лагранжа. Ищем решение в параметрическом виде. Считаем, что , , а также — это функции от параметра . Положим . Тогда
(1.3) .

Чтобы упростить выкладки, умножим (1.3) на знаменатель дроби и продифференцируем по :
;
;
(1.4) .
Далее имеем:
(1.5) .
Поставляем (1.3) и (1.5) в (1.4) и выполняем преобразования:
;
;
.
Разделим на . При ( или при и при ) имеем:
.

Разделяем переменные и интегрируем:
;
;
.
Потенцируем:
.
Заменим постоянную . Знак модуля сводится к умножению на постоянную ±1, которую включаем в .
.
Отсюда
;
.
Подставляем в (1.3):
.
Заменим постоянную :
.

Теперь рассмотрим значения , которые мы исключили из рассмотрения при выполнении операций деления. Для этого подставим эти значения в исходное уравнение (1.1),
(1.1) .
Проверим, существует ли для этих значений дополнительные решения.

1) Подставим в (1.1):
.
Отсюда . Решение удовлетворяет исходному уравнению (1.1).

2) Подставим в (1.1):
;
.
Значение не удовлетворяет исходному уравнению. Отбрасываем его.

3) Подставим в (1.1):
;
;
.
Решение удовлетворяет исходному уравнению.

Общее решение уравнения имеет вид:
;
;
.

Автор: Олег Одинцов . Опубликовано: 26-08-2012 Изменено: 24-11-2021

Условный экстремум. Метод множителей Лагранжа. Первая часть.

Для начала рассмотрим случай функции двух переменных. Условным экстремумом функции $z=f(x,y)$ в точке $M_0(x_0;y_0)$ называется экстремум этой функции, достигнутый при условии, что переменные $x$ и $y$ в окрестности данной точки удовлетворяют уравнению связи $\varphi (x,y)=0$.

Название «условный» экстремум связано с тем, что на переменные наложено дополнительное условие $\varphi(x,y)=0$. Если из уравнения связи можно выразить одну переменную через другую, то задача определения условного экстремума сводится к задаче на обычный экстремум функции одной переменной. Например, если из уравнения связи следует $y=\psi(x)$, то подставив $y=\psi(x)$ в $z=f(x,y)$, получим функцию одной переменной $z=f\left(x,\psi(x)\right)$. В общем случае, однако, такой метод малопригоден, поэтому требуется введение нового алгоритма.

Метод множителей Лагранжа для функций двух переменных.

Метод множителей Лагранжа состоит в том, что для отыскания условного экстремума составляют функцию Лагранжа: $F(x,y)=f(x,y)+\lambda\varphi(x,y)$ (параметр $\lambda$ называют множителем Лагранжа). Необходимые условия экстремума задаются системой уравнений, из которой определяются стационарные точки:

Достаточным условием, из которого можно выяснить характер экстремума, служит знак $d^2 F=F_^<''>dx^2+2F_^<''>dxdy+F_^<''>dy^2$. Если в стационарной точке $d^2F > 0$, то функция $z=f(x,y)$ имеет в данной точке условный минимум, если же $d^2F 0$, то $d^2F 0$, т.е. имеем условный минимум функции $z=f(x,y)$.

Примечание относительно формы записи определителя $H$. показать\скрыть

Некоторые авторы записывают определитель $H$ в иной форме (с знаком «-«):

В этой ситуации сформулированное выше правило изменится следующим образом: если $H > 0$, то функция имеет условный минимум, а при $H m$):

Обозначив множители Лагранжа как $\lambda_1,\lambda_2,\ldots,\lambda_m$, составим функцию Лагранжа:

Необходимые условия наличия условного экстремума задаются системой уравнений, из которой находятся координаты стационарных точек и значения множителей Лагранжа:

Выяснить, условный минимум или условный максимум имеет функция в найденной точке, можно, как и ранее, посредством знака $d^2F$. Если в найденной точке $d^2F > 0$, то функция имеет условный минимум, если же $d^2F 0.$$

Следовательно, в точке $M_1(1;3)$ функция $z(x,y)=x+3y$ имеет условный максимум, $z_<\max>=z(1;3)=10$.

Аналогично, в точке $M_2(-1;-3)$ найдем:

$$H=8\cdot\left| \begin 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \end \right|= 8\cdot\left| \begin 0 & -1 & -3\\ -1 & 1/2 & 0 \\ -3 & 0 & 1/2 \end \right|=-40$$

Так как $H 0$. Следовательно, знак $H$ противоположен знаку $\lambda$. Можно и довести вычисления до конца:

Вопрос о характере экстремума в стационарных точках $M_1(1;3)$ и $M_2(-1;-3)$ можно решить и без использования определителя $H$. Найдем знак $d^2F$ в каждой стационарной точке:

Отмечу, что запись $dx^2$ означает именно $dx$, возведённый в вторую степень, т.е. $\left( dx \right)^2$. Отсюда имеем: $dx^2+dy^2>0$, посему при $\lambda_1=-\frac<1><2>$ получим $d^2F 0$, посему в данной точке функция имеет условный максимум, $z_<\max>=\frac<500><243>$.

Исследуем характер экстремума в каждой из точек иным методом, основываясь на знаке $d^2F$:

Из уравнения связи $x+y=0$ имеем: $d(x+y)=0$, $dx+dy=0$, $dy=-dx$.

Так как $ d^2F \Bigr|_=10 dx^2 > 0$, то $M_1(0;0)$ является точкой условного минимума функции $z(x,y)=3y^3+4x^2-xy$. Аналогично, $d^2F \Bigr|_=-10 dx^2 0$, то $M_1$ – точка минимума функции $u(x)$, при этом $u_<\min>=u(0)=0$. Так как $u_^<''>(M_2) 0; \; y > 0. \end \right. $$

Все дальнейшие преобразования осуществляются с учетом $x > 0; \; y > 0$ (это оговорено в условии задачи). Из второго уравнения выразим $\lambda=-\frac<5x>$ и подставим найденное значение в первое уравнение: $5y-\frac<5x>\cdot \frac<4>=0$, $4y^2-x^2=0$, $x=2y$. Подставляя $x=2y$ в третье уравнение, получим: $\frac<4y^2><8>+\frac<2>-1=0$, $y^2=1$, $y=1$.

Так как $y=1$, то $x=2$, $\lambda=-10$. Характер экстремума в точке $(2;1)$ определим, исходя из знака $d^2F$.

В принципе, здесь можно сразу подставить координаты стационарной точки $x=2$, $y=1$ и параметра $\lambda=-10$, получив при этом:

Однако в других задачах на условный экстремум стационарных точек может быть несколько. В таких случаях лучше $d^2F$ представить в общем виде, а потом подставлять в полученное выражение координаты каждой из найденных стационарных точек:

Подставляя $x=2$, $y=1$, $\lambda=-10$, получим:

Ответ: в точке $(2;1)$ функция имеет условный максимум, $z_<\max>=6$.

В следующей части рассмотрим применение метода Лагранжа для функций большего количества переменных.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Уравнение Лагранжа

Вы будете перенаправлены на Автор24

Общий метод решения уравнения Лагранжа

Предположим, что некоторое дифференциальное уравнение первого порядка $F\left(x,y,y’\right)=0$, не разрешенное относительно производной, удалось разрешить относительно $y$, то есть представить в виде $y=f\left(x,y’\right)$.

Частным случаем дифференциального уравнения такого вида является уравнение Лагранжа $y=x\cdot \phi \left(y’\right)+\psi \left(y’\right)$, в котором $\phi \left(y’\right)\ne y’$.

Дифференциальное уравнение Лагранжа решают методом введения параметра $y’=p$.

При этом исходное дифференциальное уравнение можно переписать в виде $y=x\cdot \phi \left(p\right)+\psi \left(p\right)$.

Выполнив дифференцирование по $x$ с учетом $dy=p\cdot dx$, после несложных алгебраических преобразований получаем линейное дифференциальное уравнение относительно функции $x\left(p\right)$ и её производной $\frac $, а именно: $\frac -\frac<\phi '\left(p\right)>\cdot x=\frac<\psi '\left(p\right)>$.

Это уравнение решается известным методом, в результате чего получим его общее решение $x=F\left(p,C\right)$.

Подставив полученный результат в соотношение $y=x\cdot \phi \left(p\right)+\psi \left(p\right)$, получим $y=F\left(p,C\right)\cdot \phi \left(p\right)+\psi \left(p\right)$.

Дополнительные частные либо особые решения уравнения Лагранжа могут быть получены в результате нахождения действительных корней уравнения $p-\phi \left(p\right)=0$ и подстановки их в $y=x\cdot \phi \left(p\right)+\psi \left(p\right)$.

Решение типичных задач

Решить дифференциальное уравнение $y=-x\cdot y’+y’^ <2>$.

Имеем дифференциальное уравнение Лагранжа, в котором $\phi \left(y’\right)=-y’$ и $\psi \left(y’\right)=y’^ <2>$.

Вводим параметр $y’=p$ и получаем $y=-x\cdot p+p^ <2>$, а также $\phi \left(p\right)=-p$ и $\psi \left(p\right)=p^ <2>$.

Теперь получим уравнение вида $\frac -\frac<\phi '\left(p\right)>\cdot x=\frac<\psi '\left(p\right)>$. Для этого находим: $\phi ‘\left(p\right)=-1$; $\psi ‘\left(p\right)=2\cdot p$; $p-\phi \left(p\right)=p-\left(-p\right)=2\cdot p$.

Уравнение приобретает вид: $\frac +\frac<1> <2\cdot p>\cdot x=1$.

Применяем алгоритм решения линейного неоднородного дифференциального уравнения:

1. Стандартный вид $\frac+\frac<1><2\cdot p>\cdot x=1$, где $P\left(p\right)=\frac<1><2\cdot p>$, $Q\left(p\right)=1$.
2. Вычисляем интеграл $I_ <1>=\int P\left(p\right)\cdot dp =\int \frac<1><2\cdot p>\cdot dp =\frac<1><2>\cdot \ln \left|p\right|$.

Записываем частное решение $v\left(p\right)=e^<-\frac<1> <2>\cdot \ln \left|p\right|> $, выполняем упрощающие преобразования: $\ln v\left(p\right)=-\frac<1> <2>\cdot \ln \left|p\right|$; $\ln \left(v\left(p\right)\right)^ <2>+\ln \left|p\right|=0$; $\left(v\left(p\right)\right)^ <2>\cdot \left|p\right|=1$.

Выбираем для $v\left(p\right)$ простейший ненулевой вариант: $v\left(p\right)=\frac<1> <\sqrt

> $.