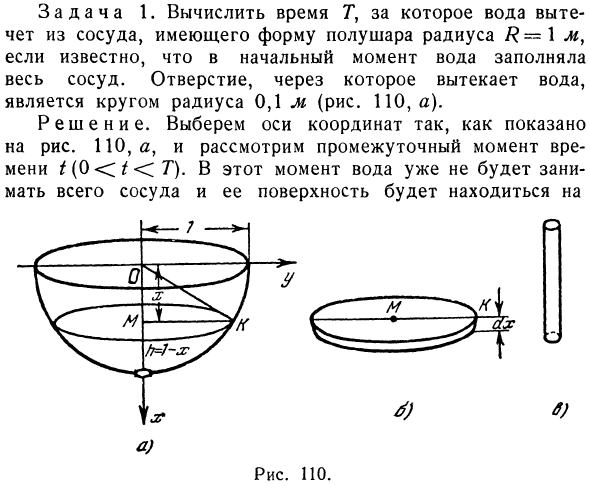
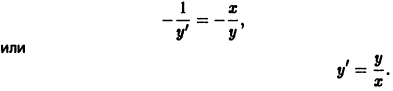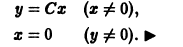Обыкновенные дифференциальные уравнения
Содержание:
Обыкновенные дифференциальные уравнения
При решении многих задач математики, техники, экономики и других отраслей науки бывает трудно установить закон, связывающий искомые и известные переменные величины. Но удается установить связь между производными или дифференциалами этих переменных, которая выражается уравнениями или системами уравнений. Такие уравнения называют дифференциальными уравнениями. Термин «дифференциальное уравнение» введен в 1676 году В. Лейбницом.
Мы рассмотрим только уравнения с функциями одной переменной и обычными производными, которые называют обычными дифференциальными уравнениями.
Основные понятия о дифференциальных уравнениях
Определение. Дифференциальным уравнением называется уравнение, которое связывает независимую переменную x, искомую функцию y = f (x) и еепроизводные или дифференциалы разных порядков, то есть уравнение

Важно понять, что искомая функция в дифференциальном уравнении входит под знак дифференциала или под знак производной.
Определение. Порядком дифференциального уравнения называется наивысший порядок производной от неизвестной функции, входящей в дифференциальное уравнение.
Так, уравнение y’ – 2 xy 2 + 5 = 0 является дифференциальным уравнением первого порядка, а уравнения y» + 2 y’ – y – sin x = 0 — дифференциальным уравнением второго порядка.
Определение. Решением дифференциального уравнения (7.1) называется такая функция y = φ (x), которая при подстановке в уравнение (7.1) превращает его в тождество.
Например, для дифференциального уравнения
y’- 2 x = 0 (7.2)
решением является функция y = x 2 . Найдем производную y’= 2x и подставим в уравнение, получим: 2x – 2x = 0, 0 ≡ 0.
Следует заметить, что y = x 2 не единственное решение уравнения. Это уравнение имеет бесконечное множество решений, которые можно записать так: y = x 2 + C.
Дифференциальные уравнения первого порядка
Определение. Дифференциальным уравнением первого порядка называется уравнение, которое связывает независимую переменную x, искомую функцию y = f (x) и ее первую производную:
F (x, y, y’) = 0. (7.3)
Поскольку производную можно записать в виде отношения дифференциалов, то в уравнение производная может не входить, а будут входить дифференциалы неизвестной функции и независимой переменной.
Если уравнение (7.2) решить относительно у’, то оно будет иметь вид:
y’= f (x, y) или 
Простые примеры показывают, что дифференциальное уравнение может иметь бесконечное множество решений. Это мы видим на примере уравнения (7.2). Легко убедиться также, что дифференциальное уравнение 


Как видим, в решение указанных дифференциальных уравнений входит произвольное число C. Предоставляя постоянной C различные значения, будем получать различные решения дифференциального уравнения.
Определение. Общим решением дифференциального уравнения (7.3) называется функция
у = φ (х, С), (7.5)
которая зависит от одной произвольной постоянной и удовлетворяет дифференциальное уравнение при произвольном значении C.
Если функция (7.5) выражается неявно, то есть в виде
Ф (х, у, С) = 0, (7.6)
то (7.6) называется общим интегралом дифференциального уравнения.
Определение. Частным решением дифференциального уравнения (7.3) называется такое решение, которое получается из общего решения (7.5) при некотором конкретном значении постоянной C.
Ф (х, у, С0) называется частным интегралом дифференциального уравнения.
На практике при решении конкретных задач часто приходится находить не все решения, а решение, которое удовлетворяет определенным начальным условиям. Одной из таких задач является задача Коши, которая для дифференциального уравнения первого порядка формулируется так: среди всех решений дифференциального уравнения (7.3) найти такое решение y, которое при заданном значении независимой переменной x = x0 равна заданному значению y0 , то есть y (x0) = y0 или 
Условие (7.7) называется начальным условием решения.
Покажем на примере, как найти частное решение дифференциального уравнения, когда известно общее решение и задано начальное условие.
Мы видим, что дифференциальное уравнение 

Ответ на вопрос о том, при каких условиях уравнение (7.4) имеет
решение, дает теорема Коши.
ТЕОРЕМА (о существовании и единственности решения). Если функция f (x, y) и ее частная производная 
Теорема Коши дает достаточные условия существования единого решения дифференциального уравнения (7.4). Заметим, что в условии теоремы не требуется существования частной производной 
График произвольного частного решения дифференциального уравнения называется интегральной кривой. Общему решению отвечает семья кривых. Так мы проверили, что уравнение 
которые проходят через начало координат (рис. 1).
Уравнение 
Если задано начальное условие 
интегральных кривых мы выбираем проходящую через точку M0 (x0; y0).
Надо заметить, что нахождение решения дифференциального уравнения часто называют интегрированием уравнения. При этом операцию интегрирования функций называют квадратурой.
Общего метода решения дифференциальных уравнений первого порядка не существует. Рассмотрим некоторые методы решения отдельных типов дифференциальных уравнений.
Дифференциальные уравнения с разделенными переменными
Определение. Уравнение вида
f1 (y) dy = f2 (x) dx, (7.8)
где f1 (y) и f2 (x) — заданные функции, называется дифференциальным уравнением с разделенными переменными.
В этом уравнении каждая из переменных находится только в той части уравнения, где находится ее дифференциал. Уравнение dy = f (x) dx является частным случаем уравнения (7.8). Чтобы решить уравнение (7.8), надо проинтегрировать обе его части: 
Понятно, что произвольную постоянную С можно записывать в любой части равенства.
Пример 1. Решить дифференциальное уравнение: 
Решение. Проинтегрируем левую и правую части уравнения, причем для удобства потенцирования, произвольную постоянную запишем в виде ln |C| получим: 


Подставляя в общее решение начальное условие, найдем С: 2 = С.
Итак,

Дифференциальные уравнения с разделяющимися переменными
Определение. Уравнение вида
f1 (x) f2 (y) + g1 (x) g2 (y) = 0 (7.9)
называется дифференциальным уравнением с разделяющимися переменными.
В этом уравнении переменные еще не разделены, но, поделив обе части уравнения на произведение f2 (y) g1 (x), получим уравнение с разделенными переменными:
Интегрируя это уравнение, запишем 
Получили общий интеграл данного уравнения.
Пример 2. Решить дифференциальное уравнение
x (y + 1) dx – (x 2 + 1) ydy = 0.
Решение. Поделим обе части этого уравнения на (y + 1) (x 2 + 1), после чего получим 
Интегрируя, получим



Пример 3. Найти частное решение дифференциального уравнения (1 + x 2 ) dy + ydx = 0, удовлетворяющее начальному условию y (0) = 1.
Решение. Отделим переменные, поделив уравнение на y ⋅ (1 + x 2 ), и проинтегрируем данное уравнение:
Получили общий интеграл дифференциального уравнения.
Используя начальное условие, найдем произвольную постоянную С:
ln 1 + arctg 0 = C, откуда C = 0.
Найденную постоянную подставим в общий интеграл и отыщем частное решение:

Однородные дифференциальные уравнения
Определение. Функция двух переменных f (x, y) называется однородной n- го измерения, если выполняется условие
Например, f (x, y) = x 2 + y 2 , f (tx, ty) = t 2 f (x 2 + y 2 ) — однородная функция второго измерения.
Определение. Дифференциальное уравнение
y ‘= f (x, y) (7.10)
называется однородным, если функция f (x, y) однородная нулевого измерения.
Покажем, что это уравнение можно свести к уравнению с разделенными переменными.
Рассмотрим функцию f (tx, ty). Сделаем замену 

Тогда уравнение (7.10) запишется в виде 
В общем случае переменные в однородном уравнение не разделяются сразу. Но, если ввести вспомогательную неизвестную функцию u = u (x) по формуле

то мы сможем превратить однородное уравнение в уравнение с разделенными переменными.
Из формулы (7.12) найдем y’ = u + xu’ и уравнение 
то есть 

После интегрирования получим 
Отсюда находим выражение для функции u, возвращаемся к переменной y = xu и получим решение однородного уравнения.
Чаще всего не удается найти функцию u явно выраженной, тогда, после интегрирования, в левую часть следует подставить 
В результате получим решение уравнения в неявном виде.
Пример 1. Найти решение однородного уравнения
Решение. Заменой y = xu сведем заданное уравнение к уравнению


Отделяя переменные, найдем




Возвращаясь к переменной y, получим общее решение: 
Линейные дифференциальные уравнения
Определение. Линейным дифференциальным уравнением первого порядка называется уравнение, которое содержит искомую функцию и ее производную в первой степени без их произведения:
y’ + P (x) y = Q (x). (7.13)
Здесь P (x), Q (x) — известные функции независимой переменной x. Например, y’ + 2 xy = x 2 .
Если Q (x) = 0, то уравнение (7.13) называется линейным однородным и является уравнением с разделяющимися переменными.
Если Q (x) ≠ 0, то уравнение (7.13) называется линейным неоднородным, которое можно решить несколькими способами.
Рассмотрим метод Бернулли, с помощью которого уравнение (7.13) можно свести к интегрированию двух дифференциальных уравнений первого порядка с разделяющимися переменными.
Решение дифференциального уравнения (7.13) ищем в виде y = u (x) v (x) или y = uv, (7.14)
где u (x), v (x) — неизвестные функции. Одну из этих функций можно взять произвольную, а другая определяется из уравнения (7.13).
Из равенства y = uv найдем производную y’:
y’= u’ ⋅ v + u⋅ v’.
Подставим y и y’ в уравнение (7.13):
u’v + uv’ + P (x) ⋅ u⋅ v = Q (x) или u’v + u (v’ + P (x) ⋅ v) = Q (x).
Выберем функцию v такой, чтобы v’ + P (x) v = 0. (7.15)
Тогда для отыскания функции u получим уравнение:
u’v = Q (x). (7.16)
Сначала найдем v из уравнения (7.15).
Отделяя переменные, имеем 
Под неопределенным интегралом здесь будем понимать какую-то одну первообразную от функции P (x), то есть v будет определенной функцией от x.
Зная v, находим u из уравнения (7.16): 
откуда
Здесь мы уже берем для u все первообразные.
Найденные функции u и v подставляем в (7.14) и получаем общее решение линейного дифференциального уравнения:

При решении конкретных примеров проще выполнять эти выкладки, чем применять громоздкую формулу (7.17).
Пример 1. Решить дифференциальное уравнение 
Решение. Решение ищем в виде y = uv, тогда y’= u’ ⋅ v + u⋅ v’.
Подставим y и y’ в уравнение: 

Выражение, стоящее в скобках, приравниваем к нулю, имеем

Отделим переменные, домножив обе части уравнения на 

После интегрирования, получим ln |v| = ln |x| (здесь ограничимся одной первообразной), откуда v = x.
Подставим v = x в уравнение (7.18):
Общее решение запишется:
y = x (x + C) = x 2 + Cx.
Пример 2. Найти частное решение дифференциального уравнения 
Решение. Заданное уравнение — это линейное неоднородное уравнение первого порядка, решение которого ищем в виде y = u⋅v.
Тогда 
Подставим v в уравнение и найдем u:
Общее решение дифференциального уравнения будет:
Подставляем начальные условия в найденное решение и находим С:
Из общего решения получаем частное решение 
Дифференциальное уравнение Бернулли
Определение. Уравнения вида


называется дифференциальным уравнением Бернулли.
Данное уравнение отличается от уравнения (7.13) только множителем y» (или x») в правой части. Для того, чтобы права часть данного уравнения была такой, как в (7.13), разделим его левую и праву часть на y»:
Сделаем замену: 
Домножим левую и правую части полученного уравнения на (n + 1) и, используя замену, получим: 
Мы получили линейное дифференциальное уравнение относительно новой переменной
Пример 1. Найти общее решение дифференциального уравнения xy’ + y = y 2 ln x.
Решение. 
Сделаем замену 
Данное уравнение решим, сделав замену z = u (x) ⋅ v (x).
Выбираем функцию v (x) так, чтобы выражение в скобках равнялось нулю, и эта функция была бы частным решением уравнения
Тогда 
Проинтегрировав правую часть этого уравнения по частям, получим 
Обыновенное дефференциальное уравнение
Обыкновенным дифференциальным уравнением называется любое соотношение, связывающее независимую переменную 


Обыкновенное дифференциальное уравнение может быть приведено к виду
Здесь 
Число 
Обыкновенные дифференциальные уравнения первого порядка, разрешенные относительно производной. уравнения, интегрируемые в квадратурах
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Основные понятия и определения
Понятие об уравнении первого порядка, разрешенном относительно производной. В соответствии со сказанным во введении, уравнение первого порядка имеет вид
В этой главе мы будем рассматривать уравнение, разрешенное относительно производной:
Наряду с этим уравнением мы всегда будем рассматривать перевернутое уравнение
используя последнее в окрестности тех точек, в которых 
Во многих случаях оказывается целесообразным «место уравнении (2) и (2′) рассматривать одно равносильное им дифференциальное уравнение
Обе переменные 

Умножая обе части уравнения (3) на некоторую функцию 
где 


Иногда уравнение записывают *з так называемой симметрической форме:
Возможно вам будут полезны данные страницы:
Решение уравнения. Предположим, что правая часть уравнения (2), 




- Существует производная
для всех значений
из интервала
(Отсюда следует, что решение
представляет собою функцию, непрерывную ею всей области определения).
- Функция
обращает уравнение (2) в тождество:
справедливое для всех значений 





Так как наряду с уравнением (2) рассматривается перевернутое уравнение (2′), то и решения 
В этом смысле в дальнейшем мы будем для краткости называть решения уравнения (2′) решениями уравнения (2).
Примеры с решением
Пример 1.
является решением уравнения
в интервале 
справедливое при всех значениях
Пример 2.
Функция 

Пример 3.
является решением уравнения
в интервале
Иногда функцию 
Системы обыкновенных дифференциальных уравнений
При решении многих задач нужно найти функции y1 = y1 (x), y2 = y2 (x), . yn = yn (x), которые удовлетворяют системе дифференциальных уравнений, содержащих независимую переменную x , искомые y1 , y2 , . yn и их производные.
Пример. Пусть материальная точка массы m имеет криволинейную траекторию движения в пространстве. Определить положение точки в любой момент времени t, когда на нее действует сила 
Положение точки в любой момент времени t определяется ее координатами x, y, z; следовательно, x, y, z являются функциями от t. Проекциями вектора скорости точки на оси координат будут производные x’ , y’ , z’.
Положим, что сила

функции определяются из уравнений динамики:
Мы получили систему трех дифференциальных уравнений второго порядка. В случае движения, когда траектория является плоской кривой, лежит, например, в плоскости Оxy, получим систему двух уравнений для определения неизвестных функций x (t) и y (t):
Рассмотрим простейшие системы дифференциальных уравнений.
Системы дифференциальных уравнений первого порядка
Система n уравнений первого порядка с n неизвестными функциями имеет вид:

где x — независимая переменная, y1, y2, . yn — неизвестные функции.
Если в левой части уравнений системы стоят производные первого порядка, а правые части уравнений вовсе не содержат производных, то такая система уравнений называется нормальной.
Решением системы называется совокупность функций y1, y2, . yn, которые превращают каждое уравнение системы в тождество относительно x.
Задача Коши для системы (7.38) состоит в нахождении функций y1, y2, . yn , удовлетворяющих систему (7.38) и заданные начальные условия:

Интегрирование системы (7.38) делают следующим образом. Дифференцируем по x первое уравнение системы (7.38): 
Заменим производные


Дифференцируем полученное уравнение и, подставив в это равенство значения производных из системы (7.38), найдем 
Продолжая дальше таким образом, получим 
В результате получаем следующую систему уравнений:

Из первых (n-1) уравнений определим y2, y3, . yn:

и подставим их значения в последнее уравнение системы (7.40) для определения y1:
Продифференцируем это выражение (n-1) раз, определим


Для того, чтобы полученное решение удовлетворяло заданным начальным условиям, остается только найти значение произвольных постоянных из уравнений (7.42) и (7.43) так, как мы это делали для одного дифференциального уравнения.
Пример 1. Проинтегрировать систему 
когда заданы начальные условия 
Решение. Дифференцируем по x первое уравнение, имеем: 



Из первого уравнения системы найдем 

Общим решением этого уравнения является

и тогда 
Подберем постоянные С1 и С2 так, чтобы выполнялись начальные условия. На основании (*) и (**) имеем:
1 = С1 – 9; 0 = С2 – 2С1 + 14, откуда С1 = 10, С2 = 6.
Таким образом, решением системы, которое удовлетворяет заданным начальным условиям, будет:
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Система дифференциальных уравнений:

где коэффициенты aij — постоянные числа, t — независимая переменная, x1 (t), . xn (t) —
неизвестные функции, называется системой линейных дифференциальных уравнений с постоянными коэффициентами.
Эту систему можно решать путем сведения к одному уравнению n-го порядка, как это было показано выше. Но эту систему можно решить и другим способом. Покажем, как это делается.
Будем искать решение системы (7.44) в виде:

Надо определить постоянные α1, α2, . αn и k так, чтобы функции (7.45) удовлетворяли систему (7.44). Подставим функции (7.45) в систему (7.44):
Сократим на e kt и преобразуем систему, сведя ее к такой системе:

Это система линейных алгебраических уравнений относительно α1, α2, . αn. Составим определитель системы:
Мы получим нетривиальные (ненулевые) решения (7.45) только при таких k, при которых определитель превратится в ноль. Получаем уравнение n-го порядка для определения k:
Это уравнение называется характеристическим уравнением для системы (7.44).
Рассмотрим отдельные случаи на примерах:
1) Корни характеристического уравнения действительны и различны. Решение системы записывается в виде:
Пример 2. Найти общее решение системы уравнений:
Решение. Составим характеристическое уравнение:

Решение системы ищем в виде
Составим систему (7.46) для корня k1 и найдем 


Откуда 


Итак, мы получили решение системы:
Далее составляем систему (7.46) для k = 4:
Откуда 
Получим второй решение системы: 
Общее решение системы будет:
2) Корни характеристического уравнения различны, но среди них есть комплексные:
k1 = α + iβ, k2 = α – iβ. Этим корням будут отвечать решения:


Можно доказать также, что истинные и мнимые части комплексного решения также будут решениями. Таким образом, получим два частных решения:

где 

Соответствующие комбинации функций (7.49) войдут в общий решение системы.
Пример 3. Найти общее решение системы
Решение. Составляем характеристическое уравнение:

Подставляем поочередно k1, k2 в систему (7.46), найдем
Запишем уравнение (7.47) и (7.48) для наших данных
Перепишем эти решения в таком виде:
За частные решения можно взять отдельно действительные и отдельно мнимые части:
Общим решением системы будет
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Методические рекомендации для преподавателей математики и студентов средних специальных учебных заведений по теме «Дифференциальные уравнения»
Разделы: Математика
I. Обыкновенные дифференциальные уравнения
1.1. Основные понятия и определения
Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную x, искомую функцию y и её производные или дифференциалы.
Символически дифференциальное уравнение записывается так:
Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.
Решением дифференциального уравнения называется такая функция 
Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение
1. Рассмотрим дифференциальное уравнение первого порядка
Решением этого уравнения является функция y = 5 ln x. Действительно, 

А это и значит, что функция y = 5 ln x– есть решение этого дифференциального уравнения.
2. Рассмотрим дифференциальное уравнение второго порядка y» — 5y’ +6y = 0. Функция 
Действительно, 
Подставляя эти выражения в уравнение, получим: 

А это и значит, что функция 
Интегрированием дифференциальных уравнений называется процесс нахождения решений дифференциальных уравнений.
Общим решением дифференциального уравнения называется функция вида 
Частным решением дифференциального уравнения называется решение, полученное из общего решения при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находится при определённых начальных значениях аргумента и функции.
График частного решения дифференциального уравнения называется интегральной кривой.
1.Найти частное решение дифференциального уравнения первого порядка
xdx + ydy = 0, если y = 4 при x = 3.
Решение. Интегрируя обе части уравнения, получим
Замечание. Произвольную постоянную С, полученную в результате интегрирования, можно представлять в любой форме, удобной для дальнейших преобразований. В данном случае, с учётом канонического уравнения окружности произвольную постоянную С удобно представить в виде 

Частное решение уравнения, удовлетворяющее начальным условиям y = 4 при x = 3 находится из общего подстановкой начальных условий в общее решение: 3 2 + 4 2 = C 2 ; C=5.
Подставляя С=5 в общее решение, получим x 2 +y 2 = 5 2 .
Это есть частное решение дифференциального уравнения, полученное из общего решения при заданных начальных условиях.
2. Найти общее решение дифференциального уравнения
Решением этого уравнения является всякая функция вида 



Следовательно, данное дифференциальное уравнение имеет бесконечное множество решений, так как при различных значениях постоянной С равенство 

Например, непосредственной подстановкой можно убедиться, что функции 

Задача, в которой требуется найти частное решение уравнения y’ = f(x,y) удовлетворяющее начальному условию y(x0) = y0, называется задачей Коши.
Решение уравнения y’ = f(x,y), удовлетворяющее начальному условию, y(x0) = y0, называется решением задачи Коши.
Решение задачи Коши имеет простой геометрический смысл. Действительно, согласно данным определениям, решить задачу Коши y’ = f(x,y) при условии y(x0) = y0,, означает найти интегральную кривую уравнения y’ = f(x,y) которая проходит через заданную точку M0(x0,y0).
II. Дифференциальные уравнения первого порядка
2.1. Основные понятия
Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,y’) = 0.
В дифференциальное уравнение первого порядка входит первая производная и не входят производные более высокого порядка.
Уравнение y’ = f(x,y) называется уравнением первого порядка, разрешённым относительно производной.
Общим решением дифференциального уравнения первого порядка называется функция вида 
Пример. Рассмотрим дифференциальное уравнение первого порядка 
Решением этого уравнения является функция 
Действительно, заменив в данном уравнении, 


Следовательно, функция 

Найти частное решение данного уравнения, удовлетворяющее начальному условию y(1)=1 Подставляя начальные условия x = 1, y =1 в общее решение уравнения 

Таким образом, частное решение получим из общего 


2.2. Дифференциальные уравнения с разделяющимися переменными
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида: y’=f(x)g(y) или через дифференциалы 
Для тех y, для которых 

Уравнение вида 
Проинтегрировав обе части уравнения 

Алгоритм решения дифференциального уравнения первого порядка с разделяющимися переменными
- Производную функции переписать через её дифференциалы
- Разделить переменные.
- Проинтегрировать обе части равенства, найти общее решение.
- Если заданы начальные условия, найти частное решение.
Решить уравнение y’ = xy
Решение. Производную функции y’ заменим на
разделим переменные
проинтегрируем обе части равенства:
Ответ:
Найти частное решение уравнения
Это—уравнение с разделенными переменными. Представим его в дифференциалах. Для этого перепишем данное уравнение в виде 
Интегрируя обе части последнего равенства, найдем
Подставив начальные значения x0 = 1, y0 = 3 найдем С 9=1-1+C, т.е. С = 9.
Следовательно, искомый частный интеграл будет 
Составить уравнение кривой, проходящей через точку M(2;-3) и имеющей касательную с угловым коэффициентом
Решение. Согласно условию
Это уравнение с разделяющимися переменными. Разделив переменные, получим:
Проинтегрировав обе части уравнения, получим:
Используя начальные условия, x = 2 и y = — 3 найдем C:
Следовательно, искомое уравнение имеет вид
2.3. Линейные дифференциальные уравнения первого порядка
Линейным дифференциальным уравнением первого порядка называется уравнение вида y’ = f(x)y + g(x)
где f(x) и g(x) — некоторые заданные функции.
Если g(x)=0 то линейное дифференциальное уравнение называется однородным и имеет вид: y’ = f(x)y
Если 
Общее решение линейного однородного дифференциального уравнения y’ = f(x)y задается формулой: 
В частности, если С =0, то решением является y = 0 Если линейное однородное уравнение имеет вид y’ = ky где k — некоторая постоянная, то его общее решение имеет вид: 
Общее решение линейного неоднородного дифференциального уравнения y’ = f(x)y + g(x) задается формулой 
т.е. равно сумме общего решения соответствующего линейного однородного уравнения и частного решения 
Для линейного неоднородного уравнения вида 
где k и b— некоторые числа и 


Пример. Решить уравнение y’ + 2y +3 = 0
Решение. Представим уравнение в виде y’ = -2y — 3 где k = -2, b= -3 Общее решение задается формулой 
Следовательно, 
Ответ:
2.4. Решение линейных дифференциальных уравнений первого порядка методом Бернулли
Нахождение общего решения линейного дифференциального уравнения первого порядка y’ = f(x)y + g(x) сводится к решению двух дифференциальных уравнений с разделенными переменными с помощью подстановки y=uv, где u и v — неизвестные функции от x. Этот метод решения называется методом Бернулли.
Алгоритм решения линейного дифференциального уравнения первого порядка
1. Ввести подстановку y=uv.
2. Продифференцировать это равенство y’ = u’v + uv’
3. Подставить y и y’ в данное уравнение: u’v + uv’ = f(x)uv + g(x) или u’v + uv’ + f(x)uv = g(x).
4. Сгруппировать члены уравнения так, чтобы u вынести за скобки:
5. Из скобки, приравняв ее к нулю, найти функцию
Это уравнение с разделяющимися переменными:
Разделим переменные и получим:
Откуда 

6. Подставить полученное значение v в уравнение 
и найти функцию 
7. Записать общее решение в виде: 

Найти частное решение уравнения y’ = -2y +3 = 0 если y =1 при x = 0
Решение. Решим его с помощью подстановки y=uv, .y’ = u’v + uv’
Подставляя y и y’ в данное уравнение, получим
Сгруппировав второе и третье слагаемое левой части уравнения, вынесем общий множитель u за скобки
Выражение в скобках приравниваем к нулю и, решив полученное уравнение, найдем функцию v = v(x)
Получили уравнение с разделенными переменными. Проинтегрируем обе части этого уравнения: 
Подставим полученное значение v в уравнение 
Это уравнение с разделенными переменными. Проинтегрируем обе части уравнения: 


Ответ:
III. Дифференциальные уравнения высших порядков
3.1. Основные понятия и определения
Дифференциальным уравнением второго порядка называется уравнение, содержащее производные не выше второго порядка. В общем случае дифференциальное уравнение второго порядка записывается в виде: F(x,y,y’,y») = 0
Общим решением дифференциального уравнения второго порядка называется функция вида 
Частным решением дифференциального уравнения второго порядка называется решение, полученное из общего 
3.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида y» + py’ +qy = 0, где pи q— постоянные величины.
Алгоритм решения однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
1. Записать дифференциальное уравнение в виде: y» + py’ +qy = 0.
2. Составить его характеристическое уравнение, обозначив y» через r 2 , y’ через r, yчерез 1: 
3.Вычислить дискриминант D = p 2 -4q и найти корни характеристического уравнения; при этом если:
а) D > 0; следовательно, характеристическое уравнение имеет два различных действительных корня 

б) D = 0; следовательно, характеристическое уравнение имеет равные действительные корни 
Общее решение
Дифференцируя общее решение, получим
Составим систему из двух уравнений
Подставим вместо 




Таким образом, искомым частным решением является функция

2. Найти частное решение уравнения


































 для всех значений
для всех значений  из интервала
из интервала  (Отсюда следует, что решение
(Отсюда следует, что решение  представляет собою функцию, непрерывную ею всей области определения).
представляет собою функцию, непрерывную ею всей области определения). обращает уравнение (2) в тождество:
обращает уравнение (2) в тождество: 


























































































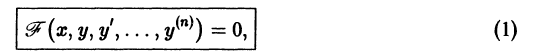
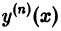 (наличие хотя бы одной производной обязательно). Здесь
(наличие хотя бы одной производной обязательно). Здесь  — заданная функция своих аргументов.
— заданная функция своих аргументов.
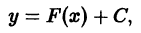
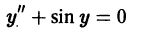
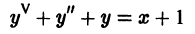
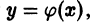 имеющая на этом интервале производные до n-го порядка включительно и такая, что подстановка функции
имеющая на этом интервале производные до n-го порядка включительно и такая, что подстановка функции 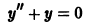
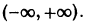 В самом деле,
В самом деле, 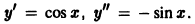 Подставив в данное уравнение найденные значения
Подставив в данное уравнение найденные значения 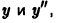 получим —
получим — 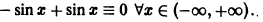
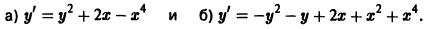
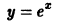
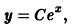
 выражающую пройденный путь как функцию времени. По условию имеем
выражающую пройденный путь как функцию времени. По условию имеем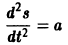
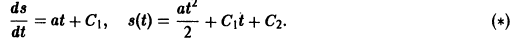
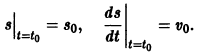
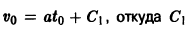 =
= 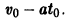 Из второго соотношения (*) при t = tо имеем
Из второго соотношения (*) при t = tо имеем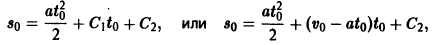

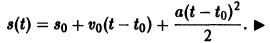

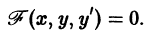


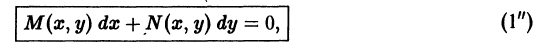
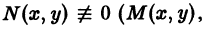
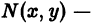 известные функции своих аргументов).
известные функции своих аргументов).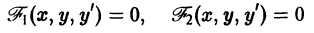
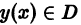 одного из этих уравнений является решением другого уравнения и наоборот. При преобразовании дифференциальных уравнений надо следить затем, чтобы преобразованное уравнение было эквивалентным исходному.
одного из этих уравнений является решением другого уравнения и наоборот. При преобразовании дифференциальных уравнений надо следить затем, чтобы преобразованное уравнение было эквивалентным исходному.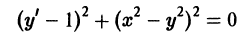
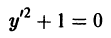
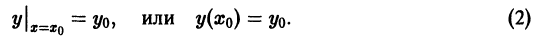
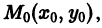 через которую должна проходить искомая интегральная кривая.
через которую должна проходить искомая интегральная кривая.
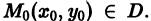 Если существует окрестность
Если существует окрестность 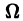 этой точки, в которой функция f(x,y)
этой точки, в которой функция f(x,y)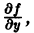 то найдется интервал
то найдется интервал 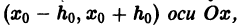 на котором существует, и притом единственная, функция
на котором существует, и притом единственная, функция 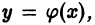 являющаяся решением уравнения (1) и принимающая при X = Xo значение Yо (рис. 1)
являющаяся решением уравнения (1) и принимающая при X = Xo значение Yо (рис. 1)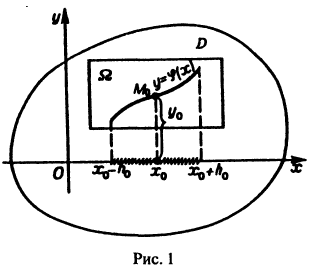
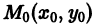 проходит одна и только одна интегральная кривая уравнения (1).
проходит одна и только одна интегральная кривая уравнения (1).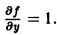 В силу теоремы 1 через каждую точку (Xо, Yо) плоскости хОу проходит единственная интегральная кривая этого уравнения.
В силу теоремы 1 через каждую точку (Xо, Yо) плоскости хОу проходит единственная интегральная кривая этого уравнения.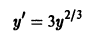
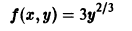
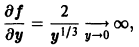
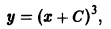
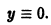
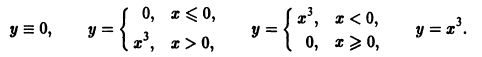
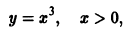
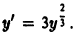 Если квадрат
Если квадрат 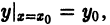 хотя в точке (Xo, Yо) не выполняются условия 1) или 2) теоремы или оба вместе.
хотя в точке (Xo, Yо) не выполняются условия 1) или 2) теоремы или оба вместе.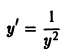
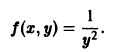
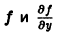 разрывны, причем
разрывны, причем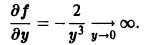
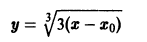
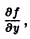 то получается следующая теорема существования решения.
то получается следующая теорема существования решения.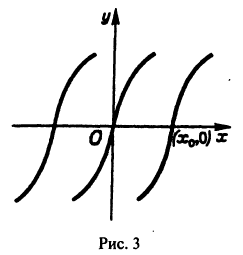
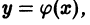 принимающее при х = х0 значение у0.
принимающее при х = х0 значение у0.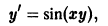
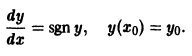

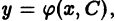 зависящих от переменной х и одной произвольной постоянной С (параметра), такое, что
зависящих от переменной х и одной произвольной постоянной С (параметра), такое, что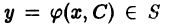 является решением уравнения (1):
является решением уравнения (1):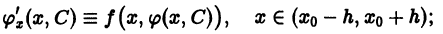
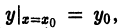 можно подобрать такое значение С0 постоянной С, что решение
можно подобрать такое значение С0 постоянной С, что решение 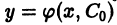 будет удовлетворять начальному условию
будет удовлетворять начальному условию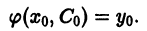
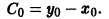
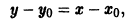
 ). Таким образом, общее решение этого дифференциального уравнения можно определить как множество всех частных решений уравнения.
). Таким образом, общее решение этого дифференциального уравнения можно определить как множество всех частных решений уравнения.
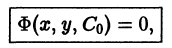
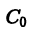 — некоторое конкретное значение постоянной С, называется частным интегралом.
— некоторое конкретное значение постоянной С, называется частным интегралом.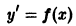
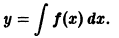
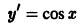
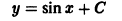
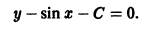
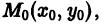 если точка
если точка 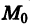 лежит на графике этого решения.
лежит на графике этого решения.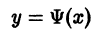
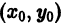 кроме этого решения проходит и другое решение уравнения (1), не совпадающее с
кроме этого решения проходит и другое решение уравнения (1), не совпадающее с 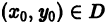 проходит единственная интегральная кривая
проходит единственная интегральная кривая 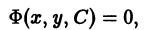
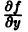 становится бесконечной.
становится бесконечной.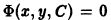 называется такая кривая, которая в каждой своей точке касается некоторой кривой семейства и каждого отрезка которой касается бесконечное множество кривых из этого семейства.
называется такая кривая, которая в каждой своей точке касается некоторой кривой семейства и каждого отрезка которой касается бесконечное множество кривых из этого семейства.
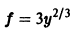 непрерывна всюду, но производная
непрерывна всюду, но производная 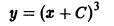
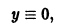
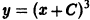 ни при каком числовом значении параметра С (включая
ни при каком числовом значении параметра С (включая 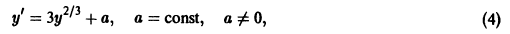
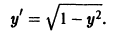

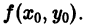
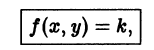
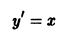
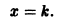
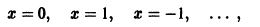
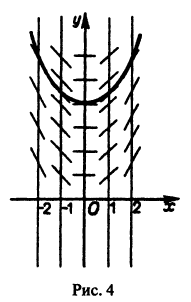
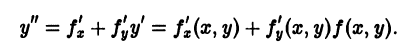
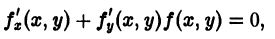
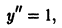


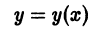
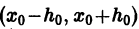 точки
точки 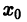 и удовлетворяющее начальному условию (3). Тогда при
и удовлетворяющее начальному условию (3). Тогда при 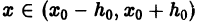 имеет место тождество
имеет место тождество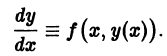
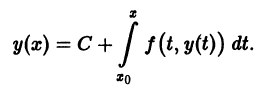
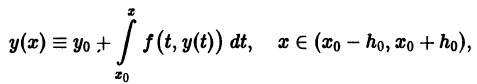
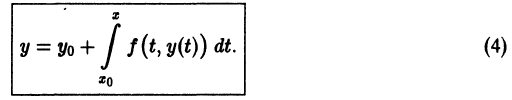
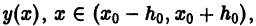 удовлетворяет интегральному уравнению (4), то, как легко проверить, у(х) является решением задачи Коши (2)-(3).
удовлетворяет интегральному уравнению (4), то, как легко проверить, у(х) является решением задачи Коши (2)-(3).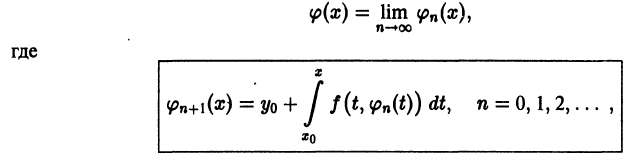
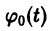 можно взять любую непрерывную на отрезке
можно взять любую непрерывную на отрезке 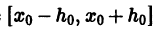 функцию, в частности,
функцию, в частности, 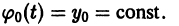
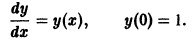
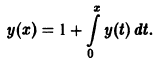
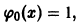
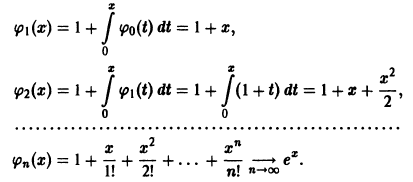
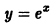 есть решение задачи.
есть решение задачи.

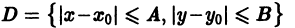 функция f(x, у) непрерывна и имеет непрерывные частные производные достаточно высокого порядка по всем аргументам, так что решение задачи Коши (1)-(2) существует, единственно и является функцией, дифференцируемой достаточное число раз.
функция f(x, у) непрерывна и имеет непрерывные частные производные достаточно высокого порядка по всем аргументам, так что решение задачи Коши (1)-(2) существует, единственно и является функцией, дифференцируемой достаточное число раз.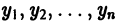 решения задачи в точках
решения задачи в точках 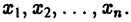 Чаще всего выбирают
Чаще всего выбирают 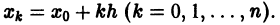 Точки Хк называют узлами сетки, а величину h > 0 — шагом сетки. Так как по определению производная
Точки Хк называют узлами сетки, а величину h > 0 — шагом сетки. Так как по определению производная 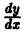 есть предел разностного отношения
есть предел разностного отношения 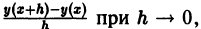 то, заменяя производную этим отношением, вместо дифференциального уравнения (1) получим разностное уравнение (разностную схему Эйлера)
то, заменяя производную этим отношением, вместо дифференциального уравнения (1) получим разностное уравнение (разностную схему Эйлера)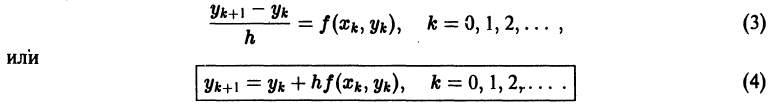
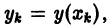 учитывая, что
учитывая, что 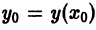 — заданная величина.
— заданная величина.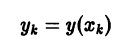
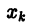 (сеточную функцию), дающую приближенное решение задачи (1)-(2). Геометрически искомая интегральная кривая у = у(х), проходящая через точку
(сеточную функцию), дающую приближенное решение задачи (1)-(2). Геометрически искомая интегральная кривая у = у(х), проходящая через точку  с вершинами в точках
с вершинами в точках 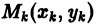 (см. рис. 5).
(см. рис. 5).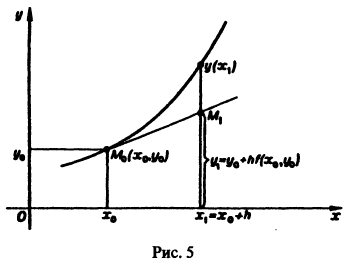
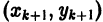 требуется знание только предыдущей вычисленной точки
требуется знание только предыдущей вычисленной точки 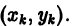 Для оценки погрешности метода на одном шаге сетки разложим точное решение у = у(х) в окрестности узла
Для оценки погрешности метода на одном шаге сетки разложим точное решение у = у(х) в окрестности узла 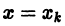 по формуле Тейлора
по формуле Тейлора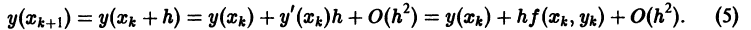
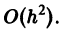 Поэтому говорят, что метод Эйлера имеет первый порядок.
Поэтому говорят, что метод Эйлера имеет первый порядок.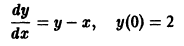
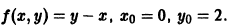 Пользуясь формулой (4),
Пользуясь формулой (4),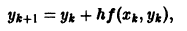
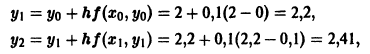
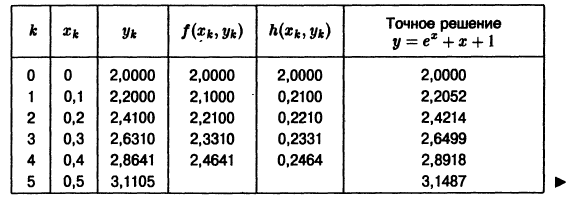
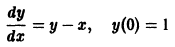
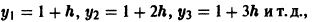 так что в этом случае ломаная Эйлера «распрямляется» и совпадает с прямой у = х + 1 — точным решением поставленной задачи Коши.
так что в этом случае ломаная Эйлера «распрямляется» и совпадает с прямой у = х + 1 — точным решением поставленной задачи Коши.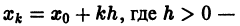 шаг сетки. В методе Рунге—Кутта величины
шаг сетки. В методе Рунге—Кутта величины 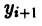 вычисляются по следующей схеме
вычисляются по следующей схеме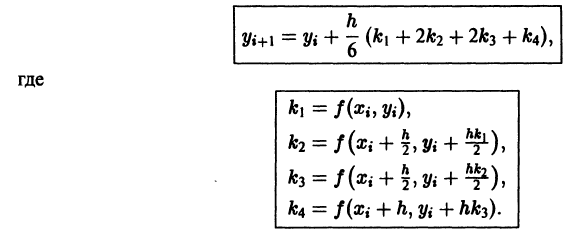

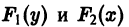 — первообразные функции
— первообразные функции 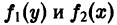 соответственно. Равенство (1) равносильно тому, что дифференциалы этих функций должны совпадать
соответственно. Равенство (1) равносильно тому, что дифференциалы этих функций должны совпадать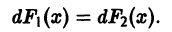

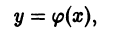
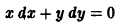
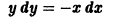
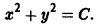
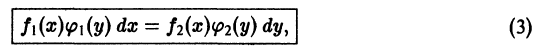
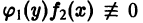 оно приводится к уравнению с разделенными переменными
оно приводится к уравнению с разделенными переменными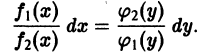
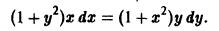
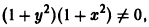 приведем его к виду
приведем его к виду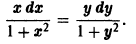

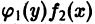 может привести к потере решений, обращающих в нуль произведение
может привести к потере решений, обращающих в нуль произведение 
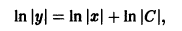
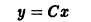
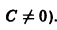 При делении на у потеряно решение
При делении на у потеряно решение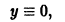
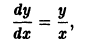
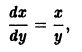


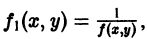 используя уравнение (4′) там, где уравнение (4) не имеет смысла, а уравнение (4′) имеет смысл.
используя уравнение (4′) там, где уравнение (4) не имеет смысла, а уравнение (4′) имеет смысл.
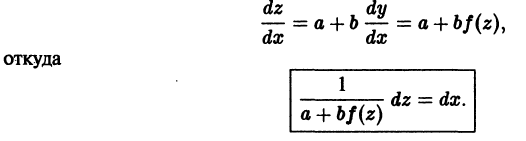
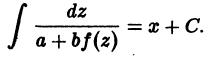
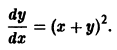
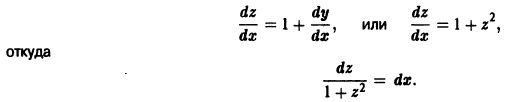

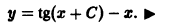
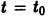 имелось
имелось 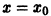 вещества.
вещества.
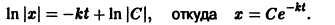
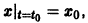 находим, что
находим, что 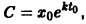 поэтому
поэтому

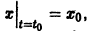 имеет вид
имеет вид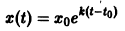

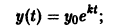

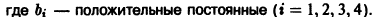
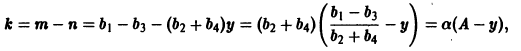
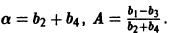
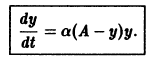

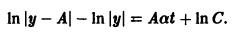
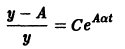
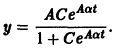
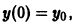 найдем уравнение логистической кривой
найдем уравнение логистической кривой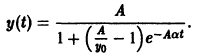
 Логистическая кривая содержит два параметра А и а. Для их определения надо иметь два дополнительных значения y(t) при каких-то t1 и t2.
Логистическая кривая содержит два параметра А и а. Для их определения надо иметь два дополнительных значения y(t) при каких-то t1 и t2.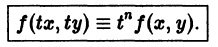
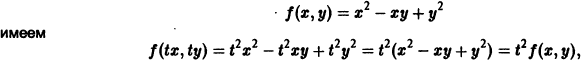
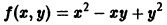 — однородная функция относительно переменных x и у второго измерения.
— однородная функция относительно переменных x и у второго измерения.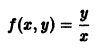
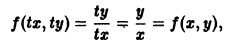
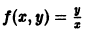 есть однородная функция нулевого измерения. Дифференциальное уравнение первого порядка
есть однородная функция нулевого измерения. Дифференциальное уравнение первого порядка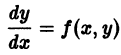
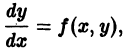
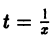 в тождестве f(tx, ty) = f(x, у), получим
в тождестве f(tx, ty) = f(x, у), получим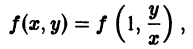
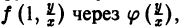 видим, что однородное относительно переменных х и у дифференциальное уравнение всегда можно представить в виде
видим, что однородное относительно переменных х и у дифференциальное уравнение всегда можно представить в виде
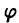 переменные не разделяются. Введем новую искомую функцию
переменные не разделяются. Введем новую искомую функцию 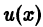 формулой
формулой 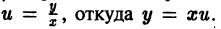 Подставляя выражение
Подставляя выражение 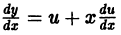 в уравнение (6), получаем
в уравнение (6), получаем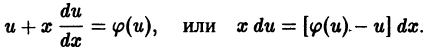
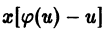 и интегрируя, находим
и интегрируя, находим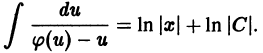
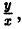 получаем общий интеграл уравнения (6).
получаем общий интеграл уравнения (6).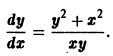
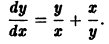
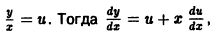 и уравнение преобразуется к виду
и уравнение преобразуется к виду
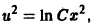 или
или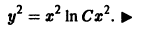
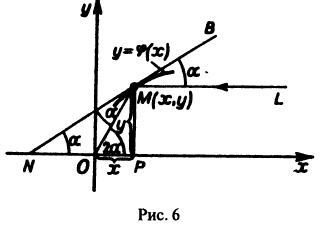
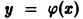 (рис.6). В точке М (х,у) падения луча L на зеркало проведем касательную BN к сечению и обозначим ее угол с осью Ох через а. Пусть N — точка пересечения этой касательной с осью Ох. По закону отражения углы NMO и BML равны. Нетрудно видеть, что угол МОР равен 2а. Так как
(рис.6). В точке М (х,у) падения луча L на зеркало проведем касательную BN к сечению и обозначим ее угол с осью Ох через а. Пусть N — точка пересечения этой касательной с осью Ох. По закону отражения углы NMO и BML равны. Нетрудно видеть, что угол МОР равен 2а. Так как 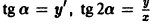
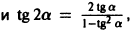 то во всякой точке кривой
то во всякой точке кривой 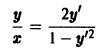
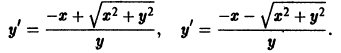
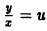 преобразуется к виду
преобразуется к виду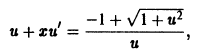
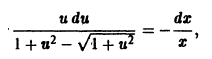
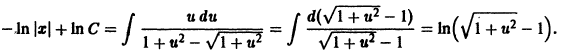
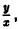 после несложных преобразований имеем
после несложных преобразований имеем
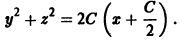
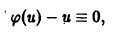
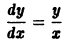
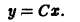
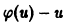 и обращается в нуль при значении
и обращается в нуль при значении 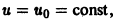 то существует также решение
то существует также решение 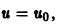 или
или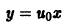

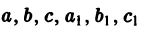 — постоянные числа, при
— постоянные числа, при 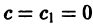 является однородным. Пусть теперь по крайней мере одно из чисел
является однородным. Пусть теперь по крайней мере одно из чисел 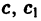 отлично от нуля. Здесь следует различать два случая.
отлично от нуля. Здесь следует различать два случая.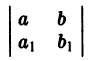 отличен от нуля. Введем новые переменные
отличен от нуля. Введем новые переменные 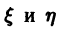 по формулам
по формулам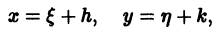
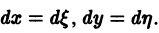 Уравнение (7) преобразуется при этом в уравнение
Уравнение (7) преобразуется при этом в уравнение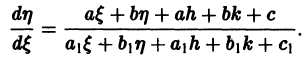

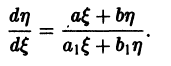
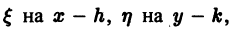 найдем общий интеграл уравнения (7).
найдем общий интеграл уравнения (7).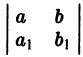 равен нулю. Система (8) в общем случае не имеет решения и изложенный выше метод неприменим. Но в этом случае
равен нулю. Система (8) в общем случае не имеет решения и изложенный выше метод неприменим. Но в этом случае 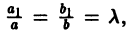 т. е. уравнение (7) имеет вид
т. е. уравнение (7) имеет вид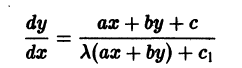
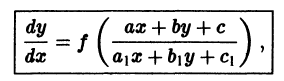
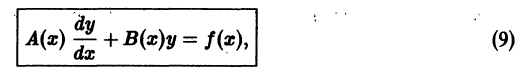
 то это уравнение называется однородным, в противном случае оно называется неоднородным. Считая
то это уравнение называется однородным, в противном случае оно называется неоднородным. Считая 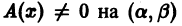 и деля обе части уравнения (9) на А(х), приведем (9) к виду
и деля обе части уравнения (9) на А(х), приведем (9) к виду
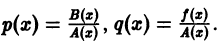
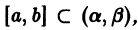 то уравнение (10) всегда имеет единственное решение, удовлетворяющее начальному условию
то уравнение (10) всегда имеет единственное решение, удовлетворяющее начальному условию 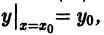 точка
точка 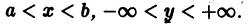
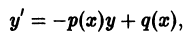
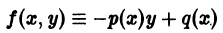
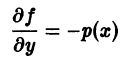

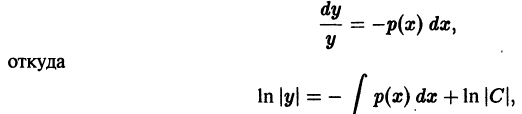

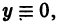 однако оно может быть включено в найденное семейство решений (12), если считать, что С может принимать значение, равное нулю. Формула (12) дает общее решение уравнения (11) в указанной выше полосе
однако оно может быть включено в найденное семейство решений (12), если считать, что С может принимать значение, равное нулю. Формула (12) дает общее решение уравнения (11) в указанной выше полосе 
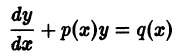
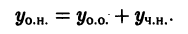
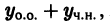 получим
получим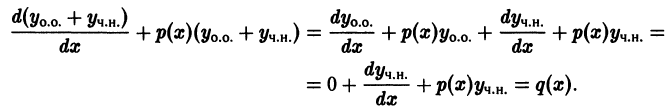
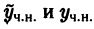 уравнения (10) является решением однородного уравнения (11)
уравнения (10) является решением однородного уравнения (11)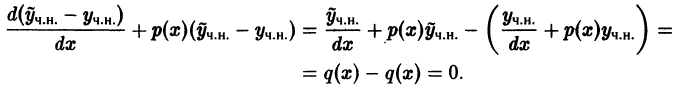
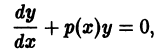
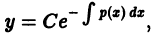

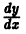 и подставляя значения
и подставляя значения 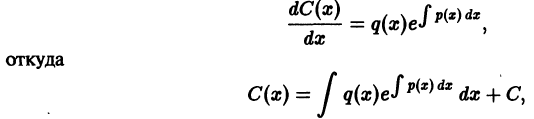
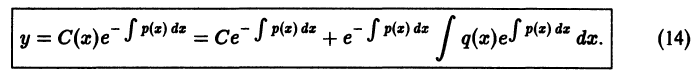
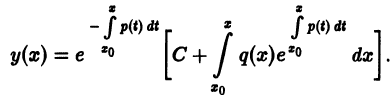
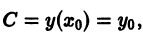 поэтому общее решение уравнения (10) можно записать в виде
поэтому общее решение уравнения (10) можно записать в виде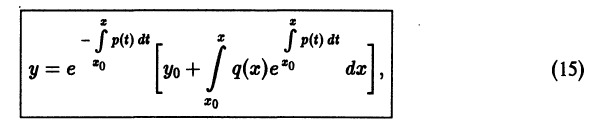
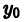 искомой функции у(х).
искомой функции у(х).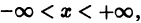 то и решение у(х) уравнения (10) с любыми начальными данными
то и решение у(х) уравнения (10) с любыми начальными данными 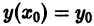 будет непрерывным и даже непрерывно дифференцируемым при всех конечных значениях х, так что интегральная кривая, проходящая через любую точку
будет непрерывным и даже непрерывно дифференцируемым при всех конечных значениях х, так что интегральная кривая, проходящая через любую точку 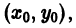 будет гладкой кривой в интервале
будет гладкой кривой в интервале 
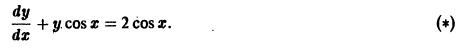
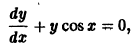
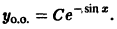

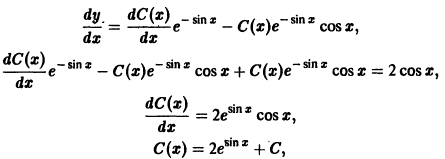
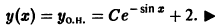
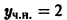 неоднородного уравнения (*) легко усматривается. Вообще, если удается «угадать» частное решение линейного неоднородного уравнения, то разыскание его общего решения значительно упрощается.
неоднородного уравнения (*) легко усматривается. Вообще, если удается «угадать» частное решение линейного неоднородного уравнения, то разыскание его общего решения значительно упрощается.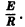
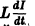 и направленная противоположно внешней ЭДС. На основании закона Ома, по которому в каждый момент t произведение силы тока на сопротивление равно фактически действующей ЭДС, получаем
и направленная противоположно внешней ЭДС. На основании закона Ома, по которому в каждый момент t произведение силы тока на сопротивление равно фактически действующей ЭДС, получаем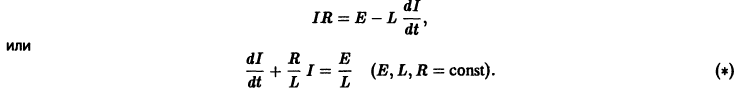
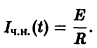
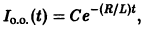
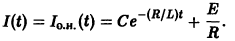
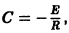 так что окончательно
так что окончательно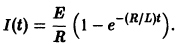
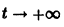 к своему стационарному значению
к своему стационарному значению 

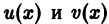 — неизвестные функции, одна из которых, например v(x), может быть выбрана произвольно. Подставляя у(х) в форме (16) в уравнение (10), после элементарных преобразований получим
— неизвестные функции, одна из которых, например v(x), может быть выбрана произвольно. Подставляя у(х) в форме (16) в уравнение (10), после элементарных преобразований получим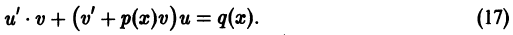
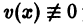 уравнения
уравнения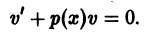
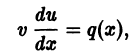
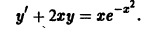
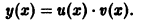
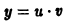 в исходное уравнение, получим
в исходное уравнение, получим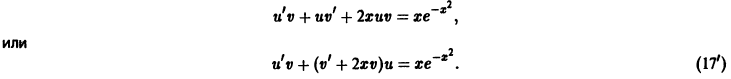
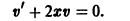
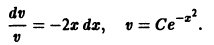
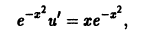
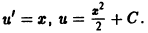
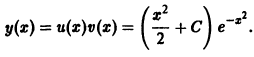
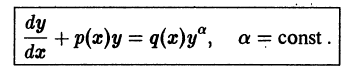
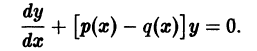
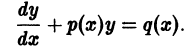
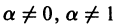 (для а нецелого считаем, что у > 0).
(для а нецелого считаем, что у > 0).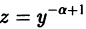 уравнение Бернулли приводится к линейному уравнению относительно функции z(x).
уравнение Бернулли приводится к линейному уравнению относительно функции z(x).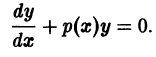
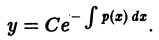

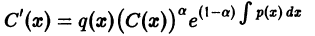
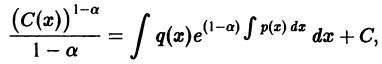
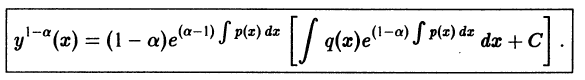
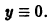
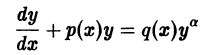
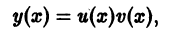
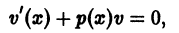
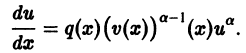
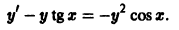
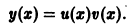
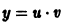 в исходное уравнение, получим
в исходное уравнение, получим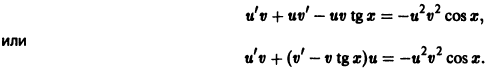
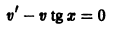
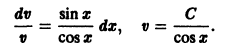
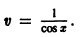 Тогда для и(х) получим уравнение
Тогда для и(х) получим уравнение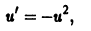
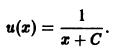
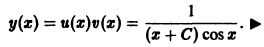
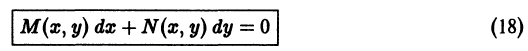
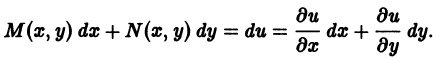

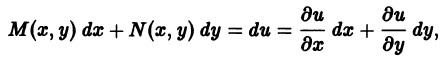
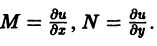 Дифференцируем первое соотношение по у, а второе по х:
Дифференцируем первое соотношение по у, а второе по х: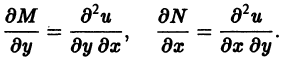
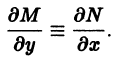
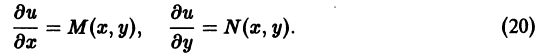
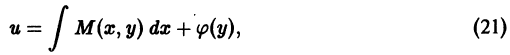
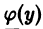 — произвольная функция от у.
— произвольная функция от у.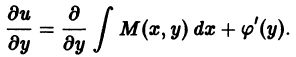
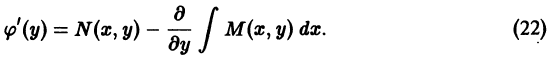
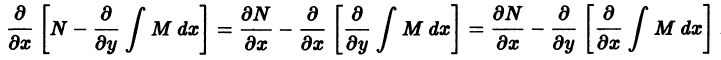
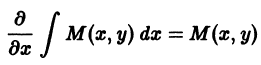
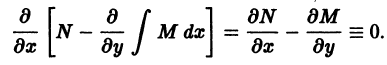
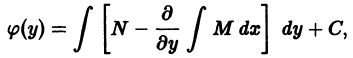
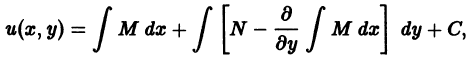
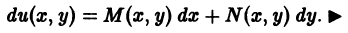

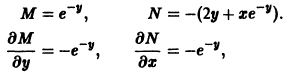
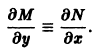
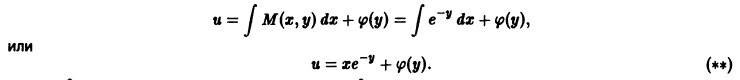
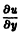 от функции и из (**) и приравнивая
от функции и из (**) и приравнивая 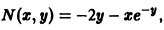 получаем
получаем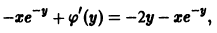
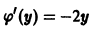 и, следовательно,
и, следовательно,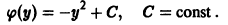
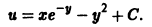
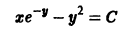
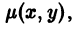 что
что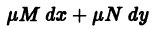
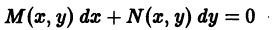
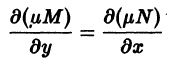
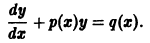
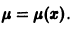
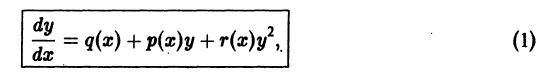
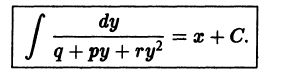
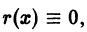 уравнение (1) оказывается линейным, в случае
уравнение (1) оказывается линейным, в случае 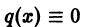 — уравнением Бернулли. В общем случае уравнение (1) не интегрируется в квадратурах.
— уравнением Бернулли. В общем случае уравнение (1) не интегрируется в квадратурах.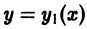 уравнения (1), тогда
уравнения (1), тогда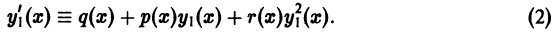
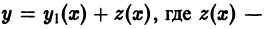 новая искомая функция, в силу тождества (2) получаем
новая искомая функция, в силу тождества (2) получаем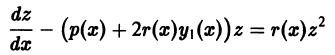
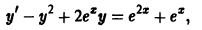
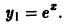
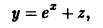

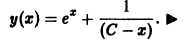
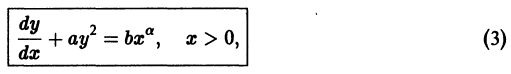
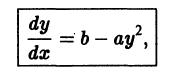
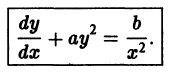
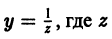 — новая неизвестная функция, находим
— новая неизвестная функция, находим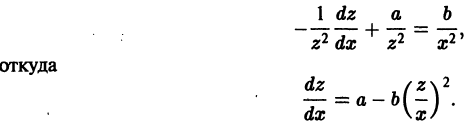
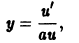
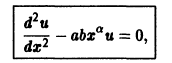

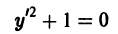
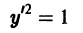
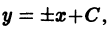 так что через каждую точку плоскости хОу проходят две взаимно перпендикулярные интегральные линии. Поле интегральных кривых уравнения
так что через каждую точку плоскости хОу проходят две взаимно перпендикулярные интегральные линии. Поле интегральных кривых уравнения 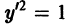 получается наложением полей уравнений
получается наложением полей уравнений 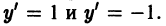 Если уравнение
Если уравнение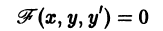
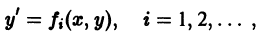
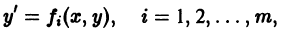
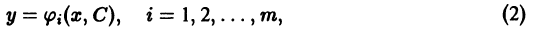
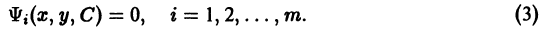
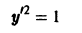
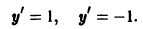
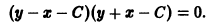
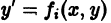 интегрируются в квадратурах. Рассмотрим некоторые методы интегрирования уравнения (1).
интегрируются в квадратурах. Рассмотрим некоторые методы интегрирования уравнения (1).
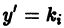 этого уравнения. Так как это уравнение не содержит
этого уравнения. Так как это уравнение не содержит 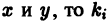 — постоянная. Интегрируя уравнение
— постоянная. Интегрируя уравнение 
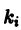 является корнем уравнения; следовательно,
является корнем уравнения; следовательно,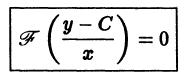
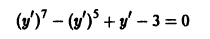
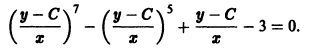

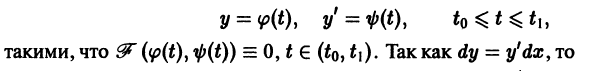
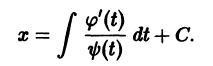
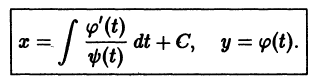
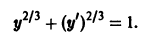
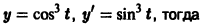
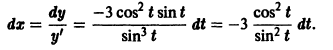
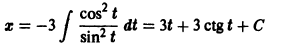
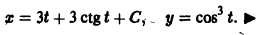
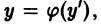 то, полагая у’ = р, получаем
то, полагая у’ = р, получаем 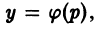 так что
так что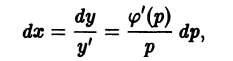
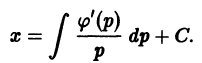
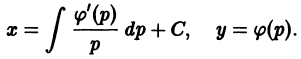
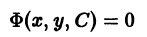
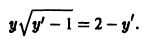
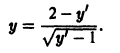
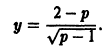
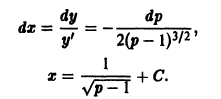
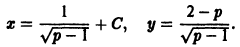
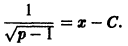
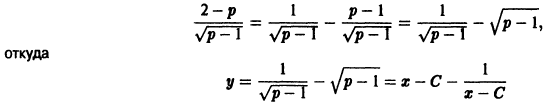

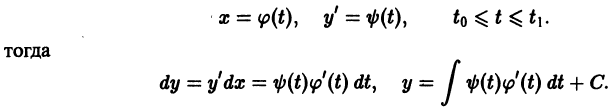
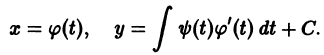
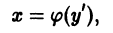
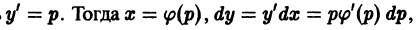 откуда
откуда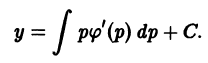
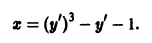
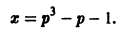
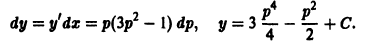
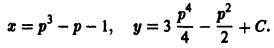

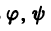 — известные функции.
— известные функции.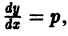 получаем
получаем
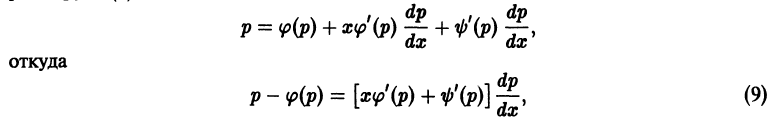
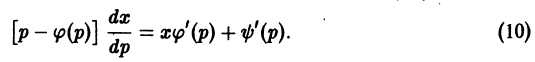
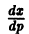 и, следовательно, легко интегрируется, например, методом вариации постоянной. Получив общее решение
и, следовательно, легко интегрируется, например, методом вариации постоянной. Получив общее решение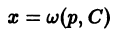
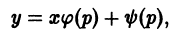
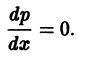
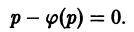
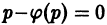 имеет действительные корни
имеет действительные корни 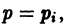 то к найденным выше решениям уравнения Лагранжа надо еще добавить решения
то к найденным выше решениям уравнения Лагранжа надо еще добавить решения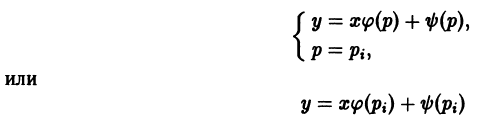

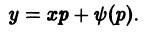
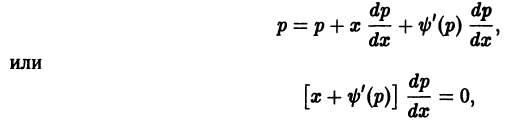
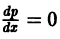 и, значит, р = С, или
и, значит, р = С, или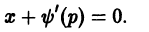
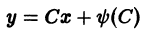
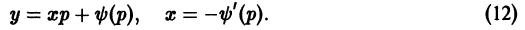
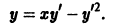
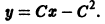
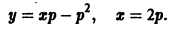
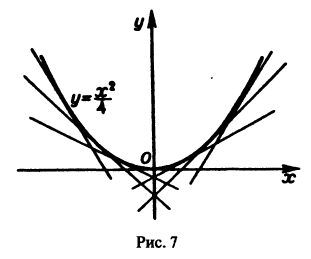
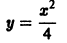
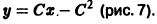
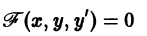
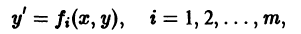
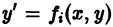 в окрестности точки
в окрестности точки 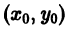 удовлетворяет условиям теоремы существования и единственности решения, то для каждого из этих уравнений найдется единственное решение, удовлетворяющее условию
удовлетворяет условиям теоремы существования и единственности решения, то для каждого из этих уравнений найдется единственное решение, удовлетворяющее условию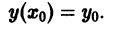
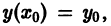 обычно понимается в том смысле, что через данную точку
обычно понимается в том смысле, что через данную точку 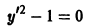
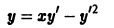
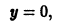
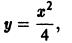
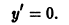
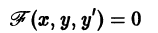
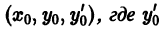 — один из действительных корней уравнения
— один из действительных корней уравнения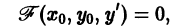
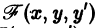 удовлетворяет условиям:
удовлетворяет условиям: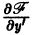 существует и отлична от нуля;
существует и отлична от нуля;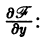
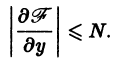
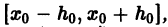 на котором существует единственное решение у = у(х) уравнения
на котором существует единственное решение у = у(х) уравнения 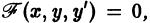 удовлетворяющее условию
удовлетворяющее условию 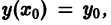 для которого
для которого 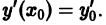
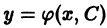 дифференциального уравнения 1-го порядка определяет семейство плоских кривых, зависящее от одного параметра С.
дифференциального уравнения 1-го порядка определяет семейство плоских кривых, зависящее от одного параметра С.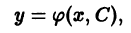


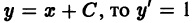 будет дифференциальным уравнением семейства прямых у = х + С.
будет дифференциальным уравнением семейства прямых у = х + С.

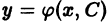 представляет собой общее решение уравнения (4).
представляет собой общее решение уравнения (4).


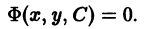
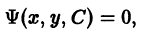
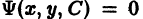 под прямым углом, т. е. чтобы касательные к кривым семейства
под прямым углом, т. е. чтобы касательные к кривым семейства 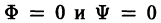 в точке (х, у) были ортогональны (рис.8). Семейство
в точке (х, у) были ортогональны (рис.8). Семейство 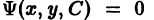 называется семейством ортогональных траекторий к
называется семейством ортогональных траекторий к 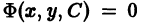 (и наоборот). Если, например, кривые семейства Ф = 0 — силовые линии некоторого силового поля, то ортогональные траектории — эквипотенциальные линии.
(и наоборот). Если, например, кривые семейства Ф = 0 — силовые линии некоторого силового поля, то ортогональные траектории — эквипотенциальные линии.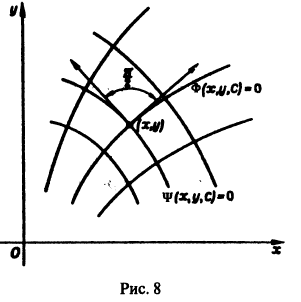
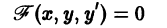
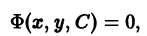
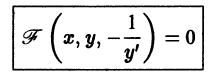
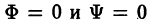 в каждой точке должны быть связаны условием ортогональности
в каждой точке должны быть связаны условием ортогональности 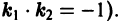
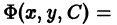 0, надо составить дифференциальное уравнение
0, надо составить дифференциальное уравнение 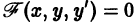 этого семейства и заменить в нем
этого семейства и заменить в нем 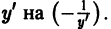 Интегрируя полученное таким образом уравнение, найдем семейство ортогональных траекторий.
Интегрируя полученное таким образом уравнение, найдем семейство ортогональных траекторий.
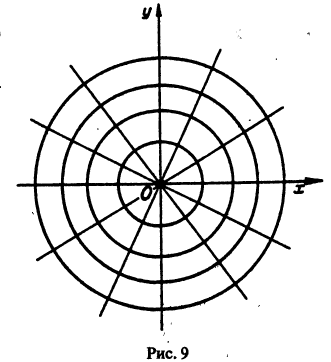
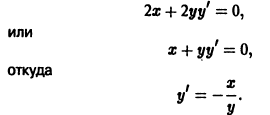
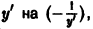 найдем дифференциальное уравнение семейства ортогональных траекторий:
найдем дифференциальное уравнение семейства ортогональных траекторий: