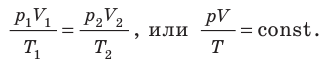Уравнение состояния вещества
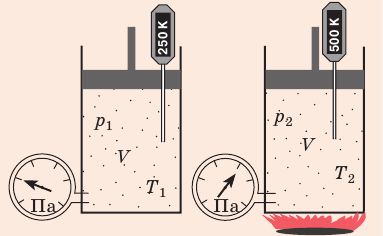
Параметры состояния связаны друг с другом. Соотношение, при котором определяется данная связь, называют уравнением состояния данного тела. В самом простом случае равновесное состояние тела определяется значением следующих параметров: давления p , объема V и температуры (масса тела или системы, как правило, известна).
Что такое идеальный газ
Уравнение состояния так называемого идеального газа является простым, но достаточно информативным.
Идеальный газ – это газ, в котором пренебрегают взаимодействием молекул между собой.
Идеальными считают разреженные газы. Особенно близки к идеальным газы гелий и водород. Идеальный газ – это упрощенная математическая модель реального газа: молекулы движутся хаотически, а соударения между молекулами и удары молекул о стенки сосуда упругие, не приводящие к потерям энергии в системе. Подобная упрощенная модель весьма удобна, поскольку не требует учета силы взаимодействия между молекулами газа. Множество реальных газов не отличаются в своем поведении от идеального газа в условиях, когда суммарный объем молекул пренебрежимо мал в сравнении с объемом сосуда (то есть при атмосферном давлении и комнатной температуре). Это дает возможность применять уравнение состояния идеального газа для сложных расчетов.
Уравнение состояния идеального газа запишем несколько раз ( 2 ) , ( 3 ) , ( 5 ) :
p V = m μ R T = ν R T ( 2 ) .
Уравнение ( 2 ) – уравнение Менделеева-Клапейрона, где m – это масса газа, μ – это молярная масса газа, R = 8 , 31 Д ж м о л ь · К – это универсальная газовая постоянная, ν – это число молей вещества.
где N – это количество молекул газа в массе m , k = 1 , 38 · 10 — 23 Д ж К , постоянная Больцмана, определяющая «долю» газовой постоянной, которая приходится на 1 молекулу и
N A = 6 , 02 · 10 23 м о л ь — 1 – это постоянная Авогадро.
Если поделить в ( 4 ) обе части на V , то получаем следующий вид записи уравнения состояния идеального газа:
где n = N V – это количество частиц в единице объема или же концентрация частиц.
Что такое реальный газ
Рассмотрим теперь более сложные системы: неидеальные газы и жидкости.
Реальный газ – это газ, между молекулами которого наблюдаются заметные силы взаимодействия.
Необходимо учитывать, что в неидеальных, плотных газах взаимодействие молекул высоко. Известно, что взаимодействие молекул очень сильно усложняет физическую картину, потому точную формулу уравнения состояния неидеального газа не получается записать в простом виде. В данном случае прибегают к приближенным формулам, найденным полу-эмпирическим путем. Самая удачная формула – это уравнение Ван-деp-Ваальса.
Взаимодействие молекул обладает сложным характером. На достаточно больших расстояниях между молекулами действуют силы притяжения. С уменьшением расстояния силы притяжения вначале растут, однако потом уменьшаются и преобразуются в силы отталкивания. Притяжение и отталкивание молекул будем рассматривать и учитывать отдельно. Уравнение Ван-дер-Ваальса, которое описывает состояние одного моля реального газа, имеет вид:
p + a V μ 2 V μ — b = R T ( 6 ) ,
где a V μ 2 – это внутреннее давление, обусловленное силами притяжения между молекулами, b – это поправка на собственный объем молекул, учитывающая действие сил отталкивания между молекулами, при этом:
b = N A 2 3 πd 3 ( 7 ) ,
где d – это диаметр молекулы. Значение a рассчитывается по формуле:
a = — 2 πN A 2 ∫ d ∞ W p ( r ) r 2 dr ( 8 ) ,
где W p ( r ) – это потенциальная энергия притяжения 2 -х молекул.
При увеличении объема значение поправок в уравнении ( 6 ) становится менее существенным. И в пределе уравнение ( 6 ) превращается в уравнение ( 2 ) . Это согласовано с тем фактом, что с уменьшением плотности реальные газы по своим характеристикам приближаются к идеальным.
Положительным в уравнении Ван-деp-Ваальса является тот факт, что данное равенство при очень больших плотностях приблизительно описывает также и свойства жидкости, в частности, плохую ее сжимаемость. Потому существует основание предполагать, что уравнение Ван-деp-Ваальса позволяет отразить и переход от жидкости к газу (либо от газа к жидкости).
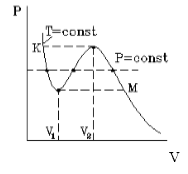
На рисунке 1 представлена изотерма Ван-дер-Ваальса для некоторого постоянного значения температуры T , которая построена из соответствующего уравнения.
В месте “извилины” (участок КМ) изотерма 3 раза пересекает изобару. На участке
V 1 , V 2 давление увеличивается с ростом объема.
Подобная зависимость невозможна. Это означает, что в этой области с веществом происходит что-то необыкновенное. Что именно, не видно в уравнении Ван-деp-Ваальса. Обратимся к опыту. В месте “извилины” на изотерме в состоянии равновесия вещество расслаивается на 2 фазы: жидкую и газообразную. Обе фазы существуют одновременно и находятся в фазовом равновесии. В таком состоянии происходит испарение жидкости и конденсация газа. Процессы протекают с такой интенсивностью, что полностью компенсируют друг друга: объем жидкости и газа со временем не изменяется.
Газ, который находится в фазовом равновесии со своей жидкостью, называется насыщенным паром. Если фазовое равновесие отсутствует, отсутствует также компенсация испарения и конденсации, тогда газ называется ненасыщенным паром.
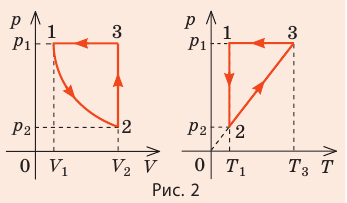
Что происходит с изотермой в области двухфазного состояния вещества (то есть в месте «извилины» изотермы Ван-деp-Ваальса)? Эксперимент показывает, что в этом месте при изменении объема давление остается неизменным. График изотермы идет параллельно оси V (рисунок 2 ).
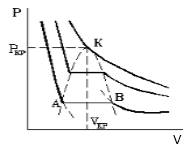
С увеличением температуры участок двухфазных состояний на изотермах уменьшается до тех пор, пока не превращается в точку (рисунок 2 ). Это особая точка К , в которой исчезает разница между жидкостью и паром. Ее называют критической точкой.
Параметры, которые соответствуют критическому состоянию, являются критическими (критическая температура, критическое давление, критическая плотность вещества).
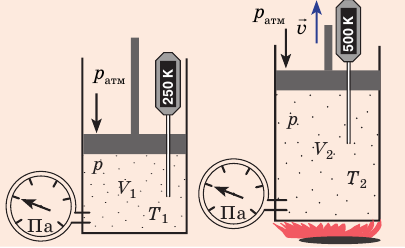
Необходимо найти величину n . В процессе, представленном на рисунке 3 , давление p
Из графика, приведенного на рисунке 3 , запишем уравнение процесса в параметрах p ( V ) :
С учетом уравнения Менделеева-Клайперона:
V вместо объема, получаем:
Моль кислорода охлаждают до — 100 ° C . Необходимо определить давление, которое оказывает газ на стенки сосуда, если занимаемый газом объем V = 0 , 1 л . Необходимо также сравнить p с давлением идеального газа p i d , если бы кислород вел себя как идеальный газ. Величина постоянных Ван-дер-Ваальса a и b , для кислорода a = 0 , 1358 П а · м 6 / м о л ь 2 , b = 3 , 167 · 10 — 5 м 3 / м о л ь .
Из уравнения Ван-Дер-Ваальса имеем:
p = R T V μ — b — a V μ 2
Переведем температуру в систему измерения: T = t + 273 , По условию T = 173 K , V = 0 , 1 л = 10 — 4 м 3 .
Произведем расчет: p = 8 , 31 · 173 ( 10 — 3 , 2 ) · 10 — 5 — 0 , 1358 ( 10 — 4 ) 2 = 75 , 61 · 10 5 ( П а ) .
Для идеального газа:
Рассчитаем: p i d = 1 · 8 , 31 · 173 10 — 4 = 143 · 10 5 ( П а ) .
Уравнение состояния идеального газа — основные понятия, формулы и определение с примерами
Содержание:
Уравнение состояния идеального газа:
Уравнения Клапейрона и Менделеева — клапейрона; законы Шарля, Гей-Люссака, Бойля — Мариотта, Авогадро, Дальтона, — пожалуй, такого количества «именных» законов нет ни в одном разделе физики. за каждым из них — кропотливая работа в лабораториях, тщательные измерения, длительные аналитические размышления и точные расчеты. нам намного проще. Мы уже знаем основные положения теории, и «открыть» все вышеупомянутые законы нам не составит труда.
Уравнение состояния идеального газа
Давление газа полностью определяется его температурой и концентрацией молекул: p=nkT. Запишем данное уравнение в виде: pV = NkT. Если состав и масса газа известны, число молекул газа можно найти из соотношения
Произведение числа Авогадро 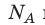
Обратите внимание! Состояние данного газа некоторой массы однозначно определяется двумя его макроскопическими параметрами; третий параметр можно найти из уравнения Менделеева — Клапейрона.
Уравнение Клапейрона
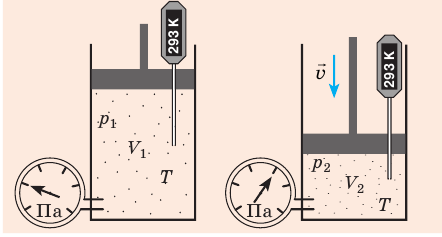
С помощью уравнения Менделеева — Клапейрона можно установить связь между макроскопическими параметрами газа при его переходе из одного состояния в другое. Пусть газ, имеющий массу m и молярную массу М, переходит из состояния (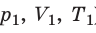
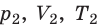
Для каждого состояния запишем уравнение Менделеева — Клапейрона: 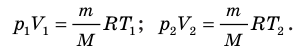
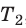
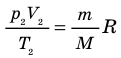
Для данного газа некоторой массы отношение произведения давления на объем к температуре газа является неизменным.
Изопроцессы
Процесс, при котором один из макроскопических параметров данного газа некоторой массы остается неизменным, называют изопроцессом. Поскольку состояние газа характеризуется тремя макроскопическими параметрами, возможных изопроцессов тоже три: происходящий при неизменной температуре; происходящий при неизменном давлении; происходящий при неизменном объеме. Рассмотрим их.
Какой процесс называют изотермическим. Закон Бойля — Мариотта
Пузырек воздуха, поднимаясь со дна глубокого водоема, может увеличиться в объеме в несколько раз, при этом давление внутри пузырька падает, поскольку вследствие дополнительного гидростатического давления воды (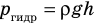
Рис. 30.2. Изотермическое сжатие газа. Если медленно опускать поршень, температура газа под поршнем будет оставаться неизменной и равной температуре окружающей среды. Давление газа при этом будет увеличиваться
Изотермический процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменной температуре.
Пусть некий газ переходит из состояния (
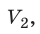
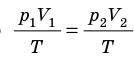
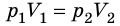
Закон Бойля — Мариотта:
Для данного газа некоторой массы произведение давления газа на его объем остается постоянным, если температура газа не изменяется:
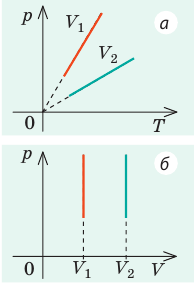
Графики изотермических процессов называют изотермами. Как следует из закона Бойля — Мариотта, при неизменной температуре давление газа данной массы обратно пропорционально его объему: 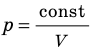
Какой процесс называют изобарным. Закон Гей-Люссака
Изобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном давлении.
Пусть некий газ переходит из состояния (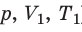
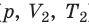
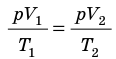
Рис. 30.4. Изобарное расширение газа. Если газ находится под тяжелым поршнем массой M и площадью S, который может перемещаться практически без трения, то при увеличении температуры объем газа будет увеличиваться, а давление газа будет оставаться неизменным и равным p
Закон Гей-Люссака
Для данного газа некоторой массы отношение объема газа к температуре остается постоянным, если давление газа не изменяется:
Графики изобарных процессов называют изобарами. Как следует из закона Гей-Люссака, при неизменном давлении объем газа данной массы прямо пропорционален его температуре: V = const⋅T. График данной зависимости — прямая, проходящая через начало координат (рис. 30.5, а). По графику видно, что с приближением к абсолютному нулю объем идеального газа должен уменьшиться до нуля. Понятно, что это невозможно, поскольку реальные газы при низких температурах превращаются в жидкости. В координатах p, V и p, T изобары перпендикулярны оси давления (рис. 30.5, б, в).
Изохорный процесс. Закон Шарля
Если газовый баллон сильно нагреется на солнце, давление в нем повысится настолько, что баллон может взорваться. В данном случае имеем дело с изохорным нагреванием.
Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном объеме.
Пусть некий газ переходит из состояния (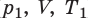
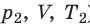
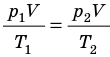
Рис. 30.6. Изохорное нагревание газа. Если газ находится в цилиндре под закрепленным поршнем, то с увеличением температуры давление газа тоже будет увеличиваться. Опыт показывает, что в любой момент времени отношение давления газа к его температуре неизменно:
Закон Шарля
Для данного газа некоторой массы отношение давления газа к его температуре остается постоянным, если объем газа не изменяется:
Графики изохорных процессов называют изохорами. Из закона Шарля следует, что при неизменном объеме давление газа данной массы прямо пропорционально его температуре: p T = ⋅ const . График этой зависимости — прямая, проходящая через начало координат (рис. 30.7, а). В координатах p, V и V, T изохоры перпендикулярны оси объема (рис. 30.7, б, в).
Пример №1
В вертикальной цилиндрической емкости под легкоподвижным поршнем находится 2 моль гелия и 1 моль молекулярного водорода. Температуру смеси увеличили в 2 раза, и весь водород распался на атомы. Во сколько раз увеличился объем смеси газов?
Анализ физической проблемы. Смесь газов находится под легкоподвижным поршнем, поэтому давление смеси не изменяется:
Решение:
Воспользуемся уравнением состояния идеального газа: pV = νRT. Запишем это уравнение для состояний смеси газов до и после распада: 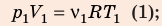
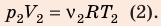

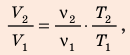
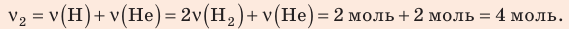
Ответ: примерно в 2,7 раза.
Пример №2
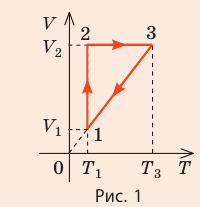
На рис. 1 представлен график изменения состояния идеального газа неизменной массы в координатах V, T. Представьте график данного процесса в координатах p, V и p, T.
Решение:
1. Выясним, какой изопроцесс соответствует каждому участку графика (рис. 1).
Зная законы, которым подчиняются эти изопроцессы, определим, как изменяются макроскопические параметры газа. Участок 1–2: изотермическое расширение; T = const, V ↑, следовательно, по закону Бойля — Мариотта p ↓. Участок 2–3: изохорное нагревание; V = const, T ↑, следовательно, по закону Шарля p ↑ . Участок 3–1: изобарное охлаждение; p = const , T ↓, следовательно, по закону Гей-Люссака V ↓ .
2. Учитывая, что точки 1 и 2 лежат на одной изотерме, точки 1 и 3 — на одной изобаре, а точки 2 и 3 на одной изохоре, и используя результаты анализа, построим график процесса в координатах p, V и p, T (рис. 2)
- Из соотношения p=nkT можно получить ряд важных законов, большинство из которых установлены экспериментально.
- Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):
— универсальная газовая постоянная.
- Уравнение Клапейрона:
- Законы, которым подчиняются изопроцессы, то есть процессы, при которых один из макроскопических параметров данного газа некоторой массы остается неизменным:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Что называется уравнением состоянием системы
Согласно молекулярно-кинетическим представлениям, тело в любом агрегатном состоянии состоит из большого числа малых обособленных частиц — молекул. Молекулы всякого вещества находятся в беспорядочном хаотическом движении, интенсивность которого зависит от температуры. Непосредственным доказательством существования хаотического движения молекул служит броуновское движение: под микроскопом можно наблюдать, что малые взвешенные в жидкости частицы всегда беспорядочно движутся, подвергаясь ударам молекул жидкости.
Для характеристики масс атомов и молекул применяют такие величины, как атомная масса А (эту величину называют также массовым числом ) и молекулярная масса М. Атомной массой А химического элемента называют отношение массы атома этого элемента к 1/12 массы атома С 12 . 1/12 массы атома С 12 , выраженная в килограммах, обозначается m ед . Тогда масса атома (в килограммах) равна Аm ед , масса молекулы — Мm ед .
Если взять простые химические вещества в таких количествах, что выполняется отношение:
то оба вещества будут содержать по одинаковому количеству атомов. Такое количество данного элемента, масса которого, выраженная в килограммах, численно равна его атомной массе, называют килограмм-атомом . Количество химически сложного вещества, масса которого, выраженная в килограммах, численно равна его молекулярной массе, называют килограмм-молекулой (киломолем). Поскольку массы килограмм-молей относятся как соответствующие молекулярные массы, киломоли всех веществ содержат одно и то же количество молекул, равное числу Авогадро :
Опытным числом найдено, что NA = 6,023·10 26 кмоль -1 . Зная число Авогадро, можно найти единичную массу: Поэтому масса любого атома равна: 1,66·10 -27 А кг, масса любой молекулы равна: 1,66·10 -27 М кг.
Произведем оценку размеров молекул. В жидкостях молекулы располагаются довольно близко друг к другу. Поэтому приближенную оценку объема одной молекулы можно сделать, разделив объем киломоля какой-либо жидкости, например, воды, на число молекул в киломоле (NA). Киломоль (т.е. 18 кг) воды занимает объем 0,018 м³. Следовательно, на одну молекулу приходится объем, равный .
Отсюда следует, что линейные размеры молекулы воды приблизительно равны .
2.1.2. Состояние системы. Внутренняя энергия.
Равновесные и неравновесные состояния газа
Системой тел называется совокупность рассматриваемых тел. Всякая система может находиться в различных состояниях, отличающихся температурой, давлением, объемом и т.п. Подобные величины, характеризующие состояние системы, называются параметрами состояния .
Не всегда какой-либо параметр имеет определенное значение. Если, например, температура неодинакова в разных точках тела, то телу нельзя приписать определенное значение параметра Т. В этом случае состояние системы будет неравновесным. Если такое тело изолировать и предоставить самому себе, то температура выровняется и примет одинаковое для всех точек значение Т, и тело перейдет в равновесное состояние. Это значение Т не изменится до тех пор, пока тело не будет выведено из равновесного состояния воздействием извне.
Равновесным состоянием системы называется такое состояние, при котором все параметры системы имеют определенные значения, остающиеся постоянными сколь угодно долго при неизменных внешних условиях.
Всякий равновесный процесс может быть представлен в виде графика, причем любое равновесное состояние изображается точкой, например точка 1 (Рис. 2.1.1).
Рис. 2.1.1. Равновесное состояние системы
Всякий процесс, т.е. переход системы из одного состояния в другое, связан с нарушением равновесия системы. Следовательно, при протекании в системе какого-либо процесса она проходит через последовательность неравновесных состояний. Если, однако, нарушение равновесия происходит очень медленно, то равновесие нарушается незначительно. Следовательно, в таком случае состояние системы в каждый момент времени является равновесным, и бесконечно медленный процесс будет состоять из непрерывной последовательности равновесных состояний. Такой процесс называется равновесным .
Внутренней энергией какого-либо тела называется энергия этого тела за вычетом кинетической энергии тела как целого и потенциальной энергии тела во внешнем поле сил. Например, при определении внутренней энергии некоторой массы газа не должна учитываться энергия движения газа вместе с сосудом и энергия, обусловленная нахождением сосуда в поле силы тяжести.
Следовательно, в понятие внутренней энергии включаются:
- кинетическая энергия хаотического движения молекул,
- потенциальная энергия взаимодействия между молекулами,
- внутримолекулярная энергия.
Внутренняя энергия является функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, ее внутренняя энергия принимает присущее данному состоянию значение. Следовательно, изменение внутренней энергии при переходе системы из одного состояния в другое будет всегда равно разности значений внутренней энергии в этих состояниях, независимо от пути, по которому совершался переход.
2.1.3. Первое начало термодинамики
Внутренняя энергия может изменяться за счет двух процессов: совершения над телом работы А’ и сообщения ему количества тепла Q. Например, поршень, вдвигаемый в сосуд, перемещаясь, совершает над газом работу А’. По третьему закону Ньютона газ при этом совершает над поршнем работу А = А’.
Сообщение телу количества тепла Q не связано с перемещением тел и, следовательно, не связано с совершением над телом макроскопической работы. В этом случае изменение внутренней энергии обусловлено тем, что отдельные молекулы более нагретого тела совершают работу над отдельными молекулами тела, нагретого менее. Совокупность микроскопических процессов, приводящих к передаче энергии от тела к телу, носит название теплопередачи.
Таким образом, приращение внутренней энергии должно быть равно сумме совершенной над системой работы и количества сообщенного системе тепла:
Обычно вместо работы внешних сил над системой A’ рассматривают работу А = — A’, совершаемую системой над внешними телами. Тогда уравнение (2.1.3) можно привести к виду:
Уравнение (2.1.4) выражает закон сохранения энергии и представляет собой содержание первого начала термодинамики : количество тепла, сообщенное системе, идет на приращение внутренней энергии системы и на совершение системой работы над внешними телами.
Внутреннюю энергию измеряют, как и работу, в системе СИ в джоулях. Есть также особая единица — 1 калория, которая равна количеству тепла, необходимому для нагревания 1 г воды от 19,5 до 20,5 °С. Опытным путем было установлено, что 1 кал = 4,18 Дж. Величина I = 4,18 Дж/кал называется механическим эквивалентом тепла .
При вычислении совершенной системой работы или полученного системой тепла приходится разбивать рассматриваемый процесс на ряд элементарных процессов, каждый из которых соответствует малому изменению параметров системы. Уравнение (2.1.4) для элементарного процесса имеет вид:
где ΔQ — элементарное количество тепла, Δ’A — элементарная работа, ΔU — приращение внутренней энергии. Надо иметь в виду, что Δ’Q и Δ’A нельзя рассматривать как приращения величин Q и А. В действительности величина совершенной телом работы и количество полученного системой тепла зависят от пути перехода системы из одного состояния в другое. Следовательно, ни А, ни Q не являются функциями состояния, в силу чего нельзя говорить о запасе тепла или работы, которыми обладала бы система в различных состояниях. Данное обстоятельство отмечено в уравнении (2.1.5) штрихом при знаке Δ. При этом ΔU — это действительно приращение внутренней энергии системы.
При переходе к бесконечно малым величинам уравнение (2.1.5) будет иметь вид:
где dU — полный дифференциал.
2.1.4. Работа, совершаемая телом
при изменении его объема
Взаимодействие данного тела с соприкасающимися с ним телами можно охарактеризовать давлением. Пусть газ заключен в цилиндрический сосуд, закрытый плотно пригнанным легко скользящим поршнем (Рис. 2.1.2).
Рис. 2.1.2. Работа газа
Если газ будет расширяться, он будет перемещать поршень и совершать над ним работу:
где f — сила, с которой газ действует на поршень.
Уравнение (2.1.7) может быть записано так:
где р — давление газа, S — площадь поршня, ΔV = SΔh — изменение объема газа.
При сжатии газа направления перемещения и силы, с которой газ действует на поршень, противоположны, вследствие чего работа будет отрицательна.
Если давление газа постоянно, работа при изменении объема равна:
В общем случае работу следует вычислять так:
2.1.5. Температура
Если несколько соприкасающихся тел находятся в состоянии теплового равновесия, т.е. не обмениваются энергией путем теплопередачи, то этим телам приписывается одинаковая температура. Если при установлении теплового контакта одно из тел передает другому энергию, то первому тему приписывают температуру, большую, чем у второго тела.
Приведем тело, выбранное нами для термометрических измерений (термометрическое тело), в тепловое равновесие с тающим льдом и припишем телу в этом случае температуру 0°С. В качестве термометрических тел выбирают, например, спирт или ртуть. Пусть в качестве признака изменения температуры выбрано изменение объема тела, и значение объема, соответствующее 0° С, обозначим V0. Затем приведем то же тело в тепловое равновесие с кипящей при атмосферном давлении водой, припишем телу в этом случае температуру 100°С, и определим соответствующий объем V100. Принимая, что объем изменяется с температурой линейно, можно состоянию тела с произвольным объемом V приписать температуру:
Установленная таким образом температурная шкала называется шкалой Цельсия.
2.1.6. Уравнение состояния идеального газа.
Экспериментальные газовые законы.
Идеальный газ — это такой газ, внутренняя энергия которого определяется только кинетической энергией составляющих его молекул. Считают также, что в этом случае объем молекул равен нулю. Потенциальной энергией взаимодействия между молекулами и внутримолекулярной энергией можно пренебречь при условии, что такой газ имеет низкую плотность и находится при не слишком высоких температуре и давлении. Этому условию обычно удовлетворяют многие газы при нормальных условиях.
Состояние некоторой массы газа определяется значениями трех параметров: давления, объема и температуры. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение других. Такая связь может быть задана аналитически в виде функции:
Соотношения, подобные (2.1.13), называются уравнениями состояния тела. Если разрешить (2.1.13) относительно какого-либо из параметров, например р, уравнение состояния примет вид:
Например, закон Бойля-Мариотта гласит, что при данной массе газа произведение давления на объем есть величина постоянная:
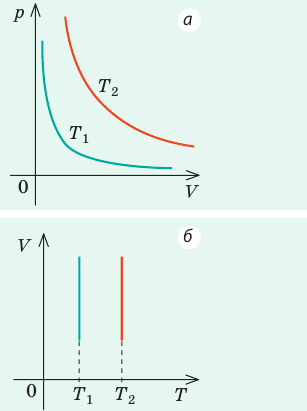
Совокупность состояний, отвечающих одной и той же температуре, изображается гиперболой на p — V диаграмме (Рис. 2.1.3).
Рис. 2.1.3. Диаграммы изотермических процессов
Каждому значению температуры соответствует своя кривая — изотерма. При изотермическом процессе точка, изображающая состояние газа, перемещается по изотерме.
Закон Гей-Люссака гласит, что при неизменном давлении объем данной массы газа меняется линейно с температурой:
Процесс (2.1.16) — изобарический (Рис. 2.1.4а).
Аналогичная зависимость имеется для давления при постоянном объеме ( закон Шарля ):
Это — изохорический процесс (Рис. 2.1.4б). В уравнениях (2.1.16) и (2.1.17) V0 — объем при 0°С, р0 — давление при 0°С. Коэффициент .
Рис. 2.1.4. Изобарический (а) и изохорический (б) процессы в газах
Все изобары и изохоры пересекают ось температур в одной и той же точке, определяемой из условия: 1 + αt = 0,откуда следует:
Сместив начало отсчета температур в эту точку, можно перейти от шкалы температур по Цельсию к температурной шкале Кельвина, или абсолютной температурной шкале. В соответствии с определением абсолютной шкалы между ней и шкалой Цельсия имеется соотношение:
Температура, равная 0 К, называется абсолютным нулем. Переходя в соотношениях (2.1.16) и (2.1.17) к абсолютной температуре, получим:
| (2.1.19) |
| (2.1.20) |
Используя (2.1.19) и (2.1.20), можно записать:
| (2.1.21) |
| (2.1.22) |
Газ, который точно следует уравнениям (2.1.15), (2.1.21) и (2.1.22), называется идеальным . Всякий реальный газ по мере убывания его плотности все больше приближается по свойствам к идеальному газу. Такие газы, как воздух, азот, кислород, при комнатной температуре и атмосферном давлении весьма близки к идеальному газу. Особенно близки по свойствам к идеальному газу гелий и водород.
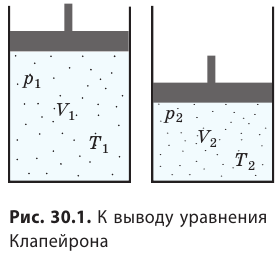
Объединяя уравнения Бойля-Мариотта и Гей-Люссака, можно найти уравнение состояния идеального газа. Для этого возьмем на диаграмме (p,V) два произвольных состояния, определяемых параметрами (p1,V1,Т1) и (p2,V2,Т2) (Рис. 2.1.5).
Рис. 2.1.5. К выводу уравнения Клапейрона
Рассмотрим переход из 1 в 2, состоящий из изотермы 1 — 1′ и изохоры 1′ — 2. Состояния 1 и 1′ лежат на одной изотерме. Следовательно, согласно (2.1.15), выполняется:
Состояния 1′ и 2 лежат на одной изохоре, поэтому, согласно (2.1.22), имеем:
Исключая из этих уравнений р’, получим:
Поскольку состояния 1 и 2 были взяты произвольно, можно утверждать, что для любого состояния будет выполняться:
где В — величина, постоянная для данной массы газа.
Согласно закону Авогадро, килограмм-молекулы всех газов занимают при одинаковых условиях одинаковый объем. При нормальных условиях объем одного киломоля любого газа равен 22,4 м³/кмоль. Отсюда следует, что в случае, когда количество газа равно одному киломолю, величина В в (2.1.26) будет одинакова для всех газов. Обозначая соответствующую киломолю величину В = R, а объем киломоля через Vкм, уравнение (2.1.26) можно записать в виде:
Это уравнение называется уравнением Клапейрона . Величина R называется универсальной газовой постоянной . Ее значение можно вычислить, подставляя в (2.1.27) давление и температуру при нормальных условиях (1 атм и 273°С) и Vкм = 22,4 м³/кмоль:
От уравнения для одного киломоля легко перейти к уравнению для любой массы газа m, приняв во внимание, что при одинаковых температуре и давлении z киломолей газа будут занимать в z больший объем, чем один киломоль: V = zVкм. Умножив (2.1.27) на z = m/μ (μ — масса киломоля), получим:
Это и есть уравнение состояния идеального газа .
2.1.7. Уравнение кинетической
теории газов для давления
Поставим задачу о вычислении давления газа на стенки сосуда исходя из молекулярно-кинетической модели газа, согласно которой газ — это совокупность одинаковых, хаотически движущихся, не взаимодействующих друг с другом на расстоянии молекул. Размеры молекул столь малы, что их суммарным объемом можно пренебречь в сравнении с объемом сосуда. Считается, что подавляющую часть времени молекула движется свободно, изредка претерпевая упругие соударения с другими молекулами или со стенками сосуда. Это — модель идеального газа.
При ударе о стенку сосуда молекула сообщает ей импульс, численно равный изменению импульса молекулы. Все направления движения равновероятны, поскольку давление газа на стенки сосуда всюду одинаково.
Скорости молекул могут быть самыми различными и должны меняться при каждом соударении, причем они могут как возрастать, так и убывать. Это следует из того, что кинетическая энергия двух молекул до и после соударения должна быть одинакова. Следовательно, возрастание скорости одной молекулы должно сопровождаться уменьшением скорости другой.
Введем некоторые упрощения:
Пусть молекулы движутся только вдоль трех взаимно перпендикулярных направлений. Если газ содержит N молекул, то в любой момент времени вдоль каждого из направлений будет двигаться N/3 молекул, причем половина из них (N/6) движется вдоль данного направления в одну сторону, половина — в другую (Рис. 2.1.6).
Рис. 2.1.6. Равнораспределение молекул
Всем молекулам припишем одинаковое значение скорости v.
Вычислим импульс, сообщаемый стенке сосуда ударяющейся об нее молекулой. До удара о стенку импульс молекулы направлен по внешней нормали к площадке ΔS и равен по величине mv (Рис. 2.1.7).
Рис. 2.1.7. Изменение импульса молекулы при упругом соударении со стенкой
В результате удара импульс меняет знак. Таким образом, приращение импульса молекулы составляет:
По третьему закону Ньютона стенка получит при ударе импульс , имеющий направление нормали. За время Δt до элемента стенки ΔS долетят все движущиеся к нему молекулы, заключенные в объеме цилиндра с основанием ΔS и высотой vΔt. Число этих молекул равно:
где где n — концентрация (число молекул в единице объема).
Умножив число ударов (2.1.30) на импульс (2.1.29), сообщаемый стенке при каждом ударе, получим суммарный импульс, сообщаемый элементу стенки за время Δt:
Относя этот импульс к промежутку времени Δt, получим силу, действующую на элемент стенки:
Эта величина, отнесенная к единице площади стенки, и есть искомое давление:
Учитывая, что кинетическая энергия поступательного движения молекулы равна , выражение для давления примет вид:
Откажемся сейчас от предположения о равенстве скоростей молекул. Пусть n1 молекул имеют скорости, практически равные v1, n2 молекул имеют скорости, практически равные v2. и вообще, ni молекул имеют скорости, практически равные vi. Очевидно, что выполняется:
Зная распределение молекул по скоростям, можно найти среднее значение скорости молекул. Для этого нужно сложить скорости всех молекул и разделить полученный результат на n:
При записи (2.1.36) учитывалось, что всего есть n1 слагаемых со скоростью v1, n2 слагаемых со скоростью v2 и т.д. Проведя аналогичные рассуждения для кинетической энергии поступательного движения молекул, можно найти среднее значение их энергии:
где — число молекул, обладающих энергией, практически равной εi. Из (2.1.37) следует, что суммарная кинетическая энергия молекул, содержащихся в единице объема, равна — произведению числа молекул на среднюю энергию одной молекулы.
Повторяя все рассуждения для давления одной частицы, но заменяя скорость на среднюю скорость, а кинетическую энергию — на среднюю кинетическую энергию, формулу для давления (2.1.33) следует записать так:
Уравнение (2.1.38) — это основное уравнение кинетической теории газов : давление равно двум третям кинетической энергии поступательного движения молекул, заключенных в единице объема.
Температура Т пропорциональна давлению идеального газа при постоянном объеме. С другой стороны, согласно (2.1.38), давление пропорционально средней энергии кинетического поступательного движения молекулы. Поэтому должно выполняться . Чтобы найти точное соотношение, умножим уравнение (2.1.38) на объем киломоля:
| (2.1.39) |
и сопоставим (2.1.39) с уравнением для идеального газа pVкм = RT. Отсюда следует, что:
где — постоянная Больцмана.
Следовательно, абсолютная температура есть величина, пропорциональная средней энергии поступательного движения одной молекулы . Этот вывод справедлив не только для газов, но и для вещества в любом агрегатном состоянии. Примечательно, что средняя энергия не зависит от массы молекулы.
Заменив в уравнении идеального газа R = NAkБ и учитывая, что концентрация газа получим важную формулу:
Если имеется смесь нескольких газов, разные по массе молекулы будут иметь различную среднюю скорость, но средняя энергия молекул будет одна и та же. Давление в этом случае будет равно:
Здесь n1, n2, и т.д. — концентрации молекул первого, второго и т.д. сорта. Тем самым оказывается, что выполняется закон Дальтона : общее давление смеси идеальных газов разного сорта равно сумме парциальных давлений газов, образующих смесь. Парциальным называют давление, обусловленное молекулами какого-либо одного сорта, при условии, что только эти молекулы присутствуют в сосуде в том количестве, в котором они содержались в смеси.
2.1.8. Равнораспределение энергии
по степеням свободы
В полученном ранее выражении:
учитывалась только энергия поступательного движения молекулы. Однако наряду с поступательным движением возможны также вращение молекулы и колебания атомов, входящих в состав молекулы. Эти виды движения также связаны с запасом энергии. Тогда общая энергия сложной молекулы определяется числом ее степеней свободы.
Числом степеней свободы механической системы называется число независимых координат, определяющих ее положение и конфигурацию в пространстве.
Так, положение в пространстве МТ (частицы газа, состоящего из атомов одного сорта) может быть полностью задано тремя координатами. Представим энергию поступательного движения такой частицы в виде суммы трех слагаемых — кинетических энергий движения молекулы по трем взаимно перпендикулярным направлениям:
где vx, vy, vz — составляющие скорости молекулы по трем осям координат.
Полная хаотичность движения молекулы позволяет считать, что средние значения кинетических энергий по трем направлениям равны друг другу:
Сопоставляя (2.1.43) и (2.1.45), получаем, что на одну степень поступательного движения частицы приходится энергия, равная:
Если бы, например, существовал такой гипотетический одноатомный «одномерный» газ, все частицы которого обладали бы способностью двигаться только вдоль одной прямой, то средняя кинетическая энергия молекулы такого газа равнялась бы .
Естественно предположить, что если бы молекула газа обладала бы еще какими-нибудь степенями свободы, то и на каждую из них приходится среднее значение кинетической энергии, равное . В классической статистической физике Л. Больцманом доказана теорема: если система молекул находится в тепловом равновесии при температуре Т, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна . Эта теорема называется законом равномерного распределения кинетической энергии по степеням свободы.
В отношении своей внутренней энергии двух- и многоатомные газы отличаются от одноатомных числом степеней свободы своих молекул. Следовательно, для вычисления внутренней энергии газа надо уметь определять число степеней свободы.
Рассмотрим простейший случай двухатомной молекулы (Н2, О2, N2, CO, NO, …) (Рис. 2.1.8).
Рис. 2.1.8. Модель двухатомной молекулы
Если расстояние между атомами не меняется (такие молекулы называются жесткими ), то такая система, в общем случае, будет иметь шесть степеней свободы. Действительно, положение и конфигурация такой молекулы определяется: тремя координатами ее центра масс, которые задают поступательное движение молекулы как целого, и тремя координатами, определяющими возможные вращения молекулы вокруг каждой из трех осей X, Y, Z.
Однако опыт и теория показывают, что вращение таких молекул вокруг оси Х, на которой лежат центры атомов, может быть возбуждено лишь при высоких температурах. При обычных температурах вращение вокруг этой оси не происходит. Это можно также объяснит тем обстоятельством, что при вращении вокруг данной оси момент инерции молекулы — наименьший, и энергетический вклад от такого движения должен быть минимальным.
Следовательно, число степеней свободы жесткой двухатомной молекулы равно 5: 3 — поступательных + 2 — вращательных.
Атомы и молекулы не всегда жестко связаны друг с другом, они могут совершать колебания относительно друг друга. Тогда потребуется еще одна координата для определения конфигурации молекулы — расстояние между атомами.
Таким образом, для двухатомной молекулы с упругой связью между атомами существует 6 степеней свободы: 3 — поступательных + 2 — вращательных + 1 — колебательная. Во многих случаях колебательные движения атомов не возбуждаются. Но если они существуют, и если их амплитуды малы по сравнению с расстоянием между атомами, то такие колебания можно считать гармоническими. Атомы в этом случае являются гармоническими осцилляторами. Однако осциллятор обладает не только кинетической, но и потенциальной энергией. Для гармонического осциллятора, как известно из механики, средние значения кинетической и потенциальной энергии равны между собой. Следовательно, если возбуждены гармонические колебания атомов, то по закону равнораспределения на каждую колебательную степень свободы молекулы приходится в виде кинетической энергии и в виде потенциальной энергии. Поэтому энергия, приходящаяся на одну колебательную степень свободы молекулы, равна kБТ.
Если молекула состоит из n атомов, не жестко связанных, то она имеет 3n степеней свободы (каждый атом имеет 3 степени свободы). Из этого числа 3 — поступательных + 3 — вращательных, за исключением случая, когда атомы расположены на одной прямой, — тогда вращательных степеней свободы — 2 (как у двухатомной молекулы).
На Рис. 2.1.9 приведена модель трехатомной молекулы.
Рис. 2.1.9. Модель трехатомной молекулы
Таким образом, нелинейная n — атомная молекула в общем случае может иметь (3n — 6) колебательных степеней свободы, а линейная — (3n — 5).
Таким образом, средняя энергия молекулы должна равняться:
где i — сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы:
Для молекул с жесткой связью между атомами i совпадает с числом степеней свободы молекулы.
2.1.9. Внутренняя энергия
и теплоемкость идеального газа
Вследствие того, что молекулы идеального газа не взаимодействуют на расстоянии, внутренняя энергия такого газа складывается из энергий отдельных молекул. Следовательно, внутренняя энергия одного киломоля идеального газа будет равна произведению числа Авогадро на среднюю энергию одной молекулы:
Внутренняя энергия произвольной массы газа m будет равна внутренней энергии одного моля, умноженной на число киломолей газа, содержащихся в массе m:
Теплоемкостью какого-либо тела называется количество тепла, которое нужно сообщить телу, чтобы повысить его температуру на один градус:
Теплоемкость одного киломоля обозначается буквой С и имеет размерность Дж/град·кмоль. Теплоемкость с единицы массы называется удельной теплоемкостью и имеет размерность Дж/град·кг. Между удельной теплоемкостью и теплоемкостью одного киломоля есть очевидное соотношение:
где μ — масса киломоля.
Величина теплоемкости зависит от условий, при которых происходит нагревание тела. Наибольший интерес представляют два случая:
- нагревание тела производится при постоянном объеме (СV);
- нагревание тела производится при постоянном давлении (Ср).
Если нагревание тела производится при постоянном объеме, тело не совершает работы над внешними телами и, согласно первому началу термодинамики (2.1.11), все тепло идет на приращение внутренней энергии тела:
Из (2.1.53) следует, что теплоемкость любого тела при постоянном объеме равна:
Подставляя в (2.1.54) соотношение (2.1.49), получим выражение для теплоемкости кило-моля идеального газа:
Отсюда следует, что теплоемкость киломоля идеального газа, измеренная при постоянном объеме, не зависит от параметров состояния газа. Исходя из (2.1.55), в этом случае можно представить внутреннюю энергию так:
Если нагревание тела производится при постоянном давлении, то газ будет расширяться, совершая над внешними телами положительную работу. Следовательно, для повышения температуры газа на один градус в этом случае потребуется больше тепла, чем при нагревании при постоянном объеме, — часть тепла будет затрачена на совершение газом работы.
Напишем уравнение первого начала термодинамики (2.1.11) для киломоля газа:
Разделив (2.1.57) на dT, получим, с учетом (2.1.54), выражение для теплоемкости кило моля идеального газа при постоянном давлении:
В соответствии с уравнением состояния идеального газа (2.1.27) и с помощью (2.1.58), имеем:
Таким образом, работа, которую совершает киломоль идеального газа при повышении его температуры на один градус при постоянном давлении, оказывается равной универсальной газовой постоянной. С учетом формулы (2.1.55) соотношение (2.1.59) примет вид:
Поделив (2.1.60) на (2.1.55), найдем характерное для каждого газа отношение γ = Ср/СV:
В Табл. 2.1.1 приводятся значения Ср, CV и γ для различных молекул, в Табл. 2.1.2 сопоставлены результаты теории с экспериментом. Теоретические значения получены в предположении, что молекулы являются жесткими, экспериментальные данные приводятся для температур, близких к комнатным.
| Молекула | Характер связи между атомами | Число степеней свободы | i | CV | Cp | γ | ||
|---|---|---|---|---|---|---|---|---|
| пос- тупат. | вра- щат. | ко- леб. | ||||||
| Одноатомная | — | 3 | — | — | 3 | 1,67 | ||
| Двухатомная | Жесткая | 3 | 2 | — | 5 | 1,40 | ||
| Двухатомная | Упругая | 3 | 2 | 1 | 7 | 1,29 | ||
| С числом атомов три и более | Жесткая | 3 | 3 | — | 6 | 1,33 | ||
| Газ | Количество атомов в молекуле | СV, 10³ Дж/град·кмоль | Сp, 10³ Дж/град·кмоль | γ | |||
|---|---|---|---|---|---|---|---|
| теор. | эксп. | теор. | эксп. | теор. | эксп. | ||
| Гелий (Не) | 1 | 12,5 | 12,5 | 20,8 | 20,9 | 1,67 | 1,67 |
| Кислород (О2) | 2 | 20,8 | 20,9 | 29,1 | 28,9 | 1,40 | 1,40 |
| Окись углерода (СО) | 2 | 20,8 | 21,0 | 29,1 | 29,3 | 1,40 | 1,40 |
| Пары воды (Н2О) | 3 | 25,0 33,2 *) | 27,8 | 33,2 41,5 *) | 36,2 | 1,33 1,25 *) | 1,31 |
*) Для i = 8, т.е. в предположении, что имеется дополнительно одна колебательная степень свободы.
Согласно классической теории, теплоемкость не должна зависеть от температуры. Однако на Рис. 2.1.10 такая зависимость для молекул водорода существует.
Рис. 2.1.10. Температурная зависимость теплоемкости водорода
Нет температурной зависимости только в определенных температурных областях, причем в таких областях теплоемкость имеет значения, соответствующие различному числу степеней свободы молекулы. Так, на участке 1 — 1′ СV = 3/2R, что означает, что молекула ведет себя как система, обладающая только поступательными степенями свободы. На участке 2 — 2′ СV = 5/2R, следовательно, при температурах, соответствующих данному интервалу, у молекулы, в дополнение к проявляющимся при более низких температурах трем поступательным степеням свободы, добавляются еще две вращательные. Наконец, при достаточно высоких температурах Cv = 7/2R, что свидетельствует о наличии при этих температурах колебательных движений в молекуле. В промежутке между названными интервалами теплоемкость с температурой монотонно возрастает, что говорит о том, что в новый вид движения вовлекаются не все молекулы сразу. Причины такого поведения могут быть объяснены только на основе квантовомеханического подхода.
2.1.10. Уравнение адиабаты идеального газа
Адиабатическим называется такой процесс, который протекает без теплообмена с окружающей средой. Для его описания подставим в уравнение первого начала термодинамики (2.1.11) выражение для внутренней энергии (2.1.58), взятое для идеального газа с массой m:
Так как для адиабатического процесса δQ = 0, то должно выполняться:
Используя уравнение состояния идеального газа, получим . Подставляя это выражение в (2.1.63), после преобразования имеем:
Данное соотношение можно представить так:
откуда следует, что при адиабатическом процессе выполняется:
Из (2.1.59) следует, что Ср — СV = R. Поэтому, вводя величину
можно представить: , тогда уравнение (2.1.66) после потенцирования примет вид:
Это уравнение адиабаты идеального газа в переменных Т и V. От этого уравнения можно перейти к уравнению в переменных p и V, используя уравнение состояния идеального газа в виде . Тогда уравнение (2.1.68) можно записать:
Это — уравнение адиабаты идеального газа в переменных p и V, называемое также уравнением Пуассона .
Во всех рассуждениях предполагалось, что состояние идеального газа в каждый момент времени характеризуется определенными значениями параметров p и Т, т.е. что рассматриваемый процесс является равновесным. Однако равновесным может быть процесс, протекающий очень медленно. Вместе с тем, поскольку в природе не существует совершенно не проводящих тепло веществ, количество тепла, которым система обменивается со своим окружением, будет тем меньше, чем меньшее время длится процесс. Следовательно, близкими к адиабатическим могут быть только быстро протекающие процессы, например, сжатие и расширение газа при распространении через него звуковой волны.
2.1.11. Политропические процессы
Все рассмотренные ранее процессы — это частные случаи политропического процесса. Политропическим называется такой процесс, при котором давление и объем идеального газа связаны соотношением:
где n может принимать значения от — ∞ до + ∞. В Табл.2.1.3 указаны значения числа n, при которых уравнение (2.1.1) соответствует одному из известных процессов.
| n | Процесс | n | Процесс |
|---|---|---|---|
| 0 | Изобарический | γ | Адиабатический |
| 1 | Изотермический | ± ∞ | Изохорический |
Первые три строки очевидны. Чтобы убедиться в справедливости четвертой строки, запишем уравнение политропы (2.1.70) для двух произвольных состояний:
Извлечем из (2.1.71) корень n — степени:
Устремляя n → ± ∞, придем к условию:
которое характеризует изохорический процесс.
2.1.12. Барометрическая формула
Атмосферное давление на какой-либо высоте h обусловлено весом вышележащих слоев газа. Пусть на этой высоте давление равно р. Тогда давление на высоте h + dh равно р + dp, причем если dh > 0, то dp
Рис. 2.1.11. К выводу барометрической формулы
где ρ — плотность газа на высоте h.
При условиях, близких к нормальным, газы, входящие в состав атмосферы, мало отличаются по своим свойствам от идеального газа. Поэтому, используя уравнение состояния идеального газа, для плотности газа можно записать:
Подставляя (2.1.76) в (2.1.75), получим:
Для случая, когда температура постоянна, интегрируя (2.1.78), получим:
где С — константа интегрирования.
Потенцируя (2.1.79) имеем соотношение:
Пусть при h = 0 выполняется р = р0. Используя это условие, из (2.1.80) получим: р (h=0) = р0 = C. Окончательное выражение для зависимости атмосферного давления газа от высоты при данной температуре примет вид:
Эта формула называется барометрической . Из нее следует, что давление убывает с высотой тем быстрее, чем тяжелее газ (чем больше μ) и чем ниже температура (Рис. 2.1.12).
Рис. 2.1.12. Зависимость давления газа от высоты и температуры (μ1 Т2)
2.1.13. Распределение Больцмана
Заменив в (2.1.81) давление р = nkБТ, получим закон изменения концентрации газа в зависимости от высоты:
Здесь n0 — число молекул в единице объема на высоте, равной нулю, n — их концентрация на высоте h. Преобразуем (2.1.82), используя связь :
Из (2.1.83) следует, что с понижением температуры число частиц на высотах, отличных от нуля, убывает, обращаясь в нуль при T = 0 (Рис. 2.1.13).
Рис. 2.1.13. Изменение концентрации частиц газа с высотой
При абсолютном нуле все молекулы расположились бы на поверхности земли. При высоких температурах, напротив, концентрация частиц слабо убывает с высотой, так что молекулы оказываются распределены по высоте почти равномерно.
Действительно, каждое конкретное распределение молекул по высоте устанавливается в результате совместного и конкурирующего действия двух факторов:
- притяжение молекул к Земле стремится расположить их на поверхности;
- тепловое движение препятствует этому и стремится распределить молекулы по высоте равномерно.
Чем больше масса и меньше температура, тем сильнее преобладает первый фактор, и молекулы окажутся сконцентрированы ближе к Земле. Например, молекулы тяжелого газа радона могут скапливаться в подвалах домов.
На разной высоте молекула с массой m обладает различным запасом потенциальной энергии:
Поэтому формулу (2.1.83) можно представить так:
где n0 — концентрация молекул там, где потенциальная энергия молекулы равна нулю.
Л. Больцман доказал, что распределение (2.1.85) справедливо не только в случае поля силы тяжести, но и в любом потенциальном поле сил для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения. Формулу (2.1.85) называют распределением Больцмана .
© ФГОУ ВПО Красноярский государственный аграрный университет, 2015
http://www.evkova.org/uravnenie-sostoyaniya-idealnogo-gaza
http://www.kgau.ru/distance/2013/et4/001/02_01.htm
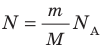
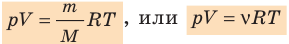
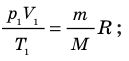
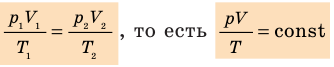
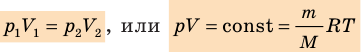

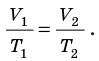
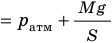
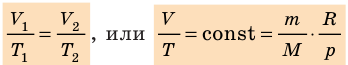
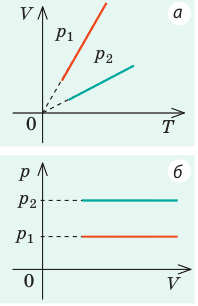

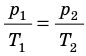
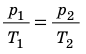
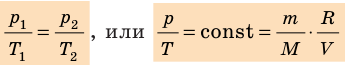

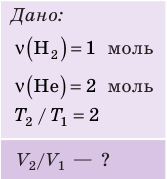
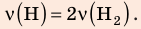

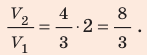
 — универсальная газовая постоянная.
— универсальная газовая постоянная.