Кинематические уравнения Эйлера и зависимость проекции вектора угловой скорости



Кинематические уравнения Эйлера
- Установить зависимость проекции вектора угловой скорости на неподвижные оси на теле, углы Эйлера , 0, p и их производные по времени. Определяется тремя углами Объект с фиксированной точкой O движется относительно координатной оси Ox1yizi (рис. 136). Система движущихся осей Oxyz прикреплена к движущемуся телу, и ее движение характеризует движение рассматриваемого тела относительно оси Oxlylzl.
Положение движущейся системы координат относительно неподвижной системы координат и, следовательно, положение самого движущегося тела Эйлера: , 0, p Изменение угла прецессии относительно оси Ox и линии узла, являющегося пересечением координатной плоскости и Ohu соответственно ОК Это означает, что угловая скорость fG направлена вдоль этой оси, а тело вращается вокруг оси прецессии Oz, перпендикулярной линии, образующей угол.
Нахождение фигуры равновесия нити на поверхности в случае, когда существует силовая функция, также приводится к определению максимума или минимума некоторого определенного интеграла. Людмила Фирмаль
Когда угол сочленения 0 между осями координат Oz и Oz изменяется, тело вращается вокруг линии узлов OK, перпендикулярных этим осям, с угловой скоростью b. d единичный вектор, направленный на положительную сторону линии узла. Если соответствующий угол поворота , образованный осью координат Ox и узловой линией OK, изменяется, объект, угловая скорость которого pk и 1c является единичным вектором оси Oz, центрируется на соответствующей оси Oz вращения, перпендикулярной этим линиям. Вращение происходит.
При изменении углов Эйлера , 0 и движение тела можно рассматривать как комплекс, состоящий из трех поворотов вокруг пересекающихся осей Oz OK и Oz угловых скоростей bj и e соответственно. Комбинация этих трех вращений соответствует вращению тела вокруг мгновенной оси с угловой скоростью d, направленной вдоль этой оси. По теореме о сложении вращения вокруг пересекающихся осей d = ^ 1 + 0 + + (16) Определяет проекцию вектора угловой скорости th на подвижную координатную ось Oxyz, прикрепленную к телу.
- Движение тела рассматривается относительно фиксированной системы отсчета Ox, y, z. При проецировании векторной суммы справа от (16) на оси Oxyz каждый член вектора должен проецироваться на эти оси. Вектор угловой скорости c 1c ориентирован вдоль оси Oz и перпендикулярен двум другим осям Ox и Oy, что дает этой оси проекцию, равную p. Рис. 137 Ох и ах на оси Угловая скорость 0i, направленная вдоль линии узла, находится в плоскости осей переноса Ox и Oy, проекция на ось Ox равна 0cos p, а проекция на ось Oy ( 0sin p).
Знак минус для проекции на ось Oy установлен потому, что расположение оси, показанное на рисунке, имеет отрицательный компонент, когда вектор 0p разложен. Направление оси Oy. Вектор проекции 0 перпендикулярен оси Oz, а проекция на эту ось равна нулю. Чтобы спроецировать вектор фА , Сначала его нужно разложить на две вертикальные составляющие на координатной оси Oxyz. Один ориентирован вдоль оси Oz, а другой в плоскости вертикальных осей Ox и Oy. У нас есть = pcos0 + sin0 (17) Где T единичный вектор в направлении вдоль линии OL. При проецировании вектора fG каждый вектор с правой стороны (17) должен проецироваться на эти оси на осях координат. Вектор fso0 k дает проекцию x cos0 только на ось Oz.
Наоборот, по закону равенства действия и противодействия, рука будет испытывать со стороны точки давление, направленное вниз и равное абсолютному весу по интенсивности и направлению. Людмила Фирмаль
Осталось спроецировать вектор 0 нахождения в плоскости координатных осей Ox и Oy. На этих осях. Поскольку линии узла перпендикулярны координатным осям Oz и Ozt и, таким образом, также перпендикулярны линиям, линия узла OK также располагается в плоскости этих осей (рис. 1371, линия OL, на которую направлен вектор проекции sin0 T, и Линии узлов перпендикулярны друг другу), поскольку угол p между осями OL Ox и OK, расположенными в плоскости этих осей, представляет собой угол между осями Oy и OL, перпендикулярными им Проекция вектора fwO Г на Oy равна i sin0cos p, а ось Oh— isin0sin p.
Рассматривая проекцию вектора, полученную из правой части (17), объединяя проекции на оси координат векторов, содержащихся в правой части (16), получается уравнение движения Эйлера. Косинус угла оси прецессии Ozt выражается с помощью координатной оси Oxyz, прикрепленной к движущемуся телу через угол Эйлера. Вектор угловой скорости направлен вдоль оси прецессии Ozt. Следовательно, коэффициент в уравнении Сожа является вычисленным косинусом вышеуказанного угла. Покажите их для краткости, 2, 3, y = cos (z ,, Ax) = sin0sin p; Y2 = cos (z1 ,, p) = sin0cos p; (18) y3 = cos (z, Az) = cos0.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Please wait.
We are checking your browser. gufo.me
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6e130b502f963a71 • Your IP : 85.95.188.35 • Performance & security by Cloudflare
Кинематические уравнения в обобщенных координатах. Углы Эйлера, Крылова, кватернионы.
В курсе теоретической механики сферическое движение задавалось углами Эйлера (рис. 1.2) – углом прецессии y (поворот вокруг неподвижной оси Oz), углом нутации q (поворот вокруг полуподвижной оси ОК – линии пересечения плоскостей Oxy и Oξη, называемой линией узлов) и углом собственного вращения j (поворот вокруг связанной с телом оси Oz).
Рис. 1.2. Система ориентационных углов Эйлера твердого тела
Углы Эйлера перечислены здесь в порядке поворотов, которые надо совершить над неподвижной СК Oxyz чтобы она совместилась с подвижной СК Oξηζ. Использование углов Эйлера в сферическом движении делалось для демонстрации принципиальной возможности решения соответствующих задач кинематики. Здесь же у нас стоит задача более оптимально описать такое движение. Кинематические соотношения, выражающие проекции угловой скорости тела на оси связанной СК через угловые скорости указанных углов представляются для углов Эйлера формулами (сверены с программой КИДИМ):
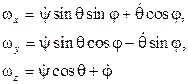
Несмотря на лаконичность такого задания положения тела при сферическом движении (3 степени свободы, 3 координаты), в современной механике оно используется редко. Это объясняется, в частности тем, что формулы вычисления обобщенных скоростей через проекции угловой скорости тела (обратные кинематические соотношения) содержат особенности и несимметричны, что затрудняет анализ результатов и приводит к вычислительным погрешностям. Для углов Эйлера эти соотношения представляются формулами:
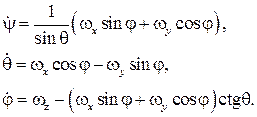
Более предпочтительным является использование параметров Родрига-Гамильтона, кватернионов, параметров Кейли-Клейна.
Докажем теорему д’Аламбера-Эйлера.
Перемещение тела, имеющего неподвижную точку, из одного положения в другое, можно осуществить поворотом вокруг некоторой оси, проходящей через неподвижную точку.
Движение тела полностью определяется движением любого треугольника, принадлежащего телу. Поэтому для сферического движения это эквивалентно движению двух точек на некоторой сфере, центр которой совпадает с неподвижной точкой, или движению дуги, соединяющей эти точки. Предположим, что в результате перемещения тела за время Dt некоторая точка А переместилась по сфере в положение В (рис. 1.3). В то же самое время точка, которая находилась в положении В, заняла новое положение С.
 Рис. 1.3. Рис. 1.3. | Плоскость ABC пересекает неподвижную сферу по окружности (малого или большого круга). Если D один из полюсов этого круга на сфере, то  , т.к. они равнобедренные сферические и , т.к. они равнобедренные сферические и 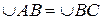 , так как они являются двумя положениями одной и той же дуги сферы АВ. , так как они являются двумя положениями одной и той же дуги сферы АВ.  по построению (равноудалены от полюса). Следовательно, по построению (равноудалены от полюса). Следовательно, 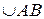 может быть совмещена с может быть совмещена с 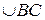 при помощи вращения вокруг оси OD на угол ADB. Теорема доказана. при помощи вращения вокруг оси OD на угол ADB. Теорема доказана. |
Параметры Родрига-Гамильтона. Для задания такого поворота, который будем называть конечным поворотом тела, очевидно, надо задать положение оси, направление и угол поворота. Ось поворота можно задать единичным вектором, направленным в ту сторону, откуда поворот тела будет наблюдаться против часовой стрелки. Этот вектор определится своими проекциями на оси некоторой СК (направляющими косинусами его углов с осями этой СК). Таким образом, конечный поворот определится четырьмя скалярными величинами ‑ проекциями единичного вектора оси и величиной угла самого поворота вокруг этой оси.
Воспользуемся для задания таких четырех величин параметрами Родрига-Гамильтона, которые обозначим здесь λ0, λ1, λ2, λ3. Последние три параметра обычно объединяют в вектор 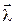
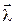


Очевидно, что 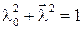
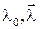

Не останавливаясь на анализе свойств и применении введенных таким образом параметров Родрига-Гамильтона, рассмотрим еще более обобщающие величины для этого – кватернионы.
http://gufo.me/dict/bse/%D0%AD%D0%B9%D0%BB%D0%B5%D1%80%D0%B0_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D1%8F
http://helpiks.org/5-15011.html



