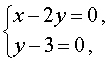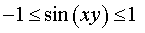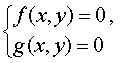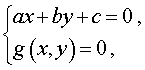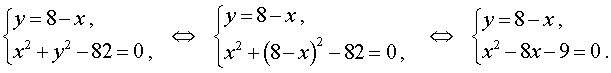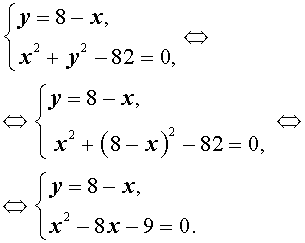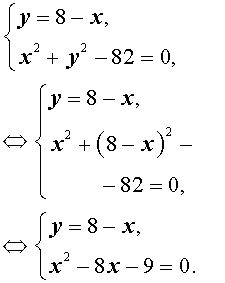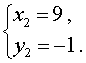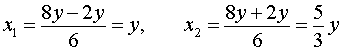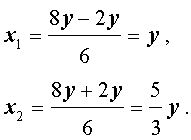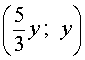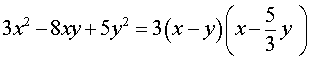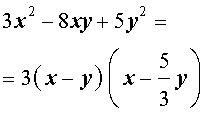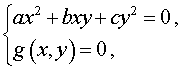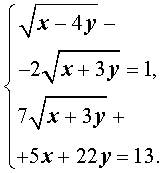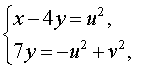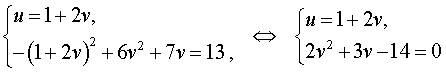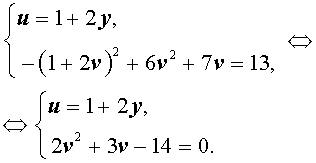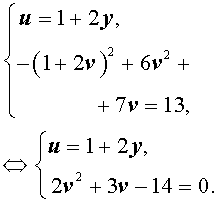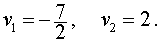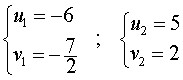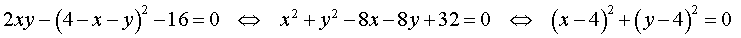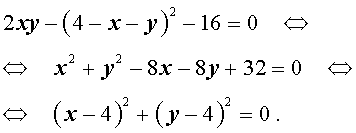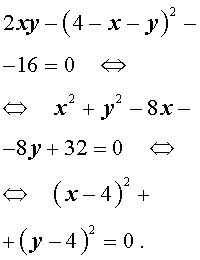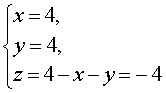Что означает решить систему нелинейных уравнений

Системы с нелинейными уравнениями

Нелинейные уравнения с двумя неизвестными

Системы из двух уравнений, одно из которых линейное

Однородные уравнения второй степени с двумя неизвестными

Системы из двух уравнений, одно из которых однородное

Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное

Примеры решения систем уравнений других видов

Нелинейные уравнения с двумя неизвестными

Определение 1 . Пусть A – некоторое множество пар чисел (x ; y) . Говорят, что на множестве A задана числовая функция z от двух переменных x и y , если указано правило, с помощью которого каждой паре чисел из множества A ставится в соответствие некоторое число.

Задание числовой функции z от двух переменных x и y часто обозначают так:

причем в записи (1) числа x и y называют аргументами функции , а число z – значением функции , соответствующим паре аргументов (x ; y) .

Определение 2 . Нелинейным уравнением с двумя неизвестными x и y называют уравнение вида

где f (x , y) – любая функция, отличная от функции

где a , b , c – заданные числа.

Определение 3 . Решением уравнения (2) называют пару чисел (x ; y) , для которых формула (2) является верным равенством.

Пример 1 . Решить уравнение

Решение . Преобразуем левую часть уравнения (3):

Таким образом, уравнение (3) можно переписать в виде

Поскольку квадрат любого числа неотрицателен, то из формулы (4) вытекает, что неизвестные x и y удовлетворяют системе уравнений

решением которой служит пара чисел (6 ; 3) .

Пример 2 . Решить уравнение

вытекает, что уравнение (5) решений не имеет.

Ответ : Решений нет.

Пример 3 . Решить уравнение

Следовательно, решением уравнения (6) является бесконечное множество пар чисел вида

где y – любое число.

Системы из двух уравнений, одно из которых линейное

Определение 4 . Решением системы уравнений

называют пару чисел (x ; y) , при подстановке которых в каждое из уравнений этой системы получается верное равенство.

Системы из двух уравнений, одно из которых линейное, имеют вид

где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .

Пример 4 . Решить систему уравнений

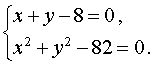(7)

Решение . Выразим из первого уравнения системы (7) неизвестное y через неизвестное x и подставим полученное выражение во второе уравнение системы:

Таким образом, решениями системы (7) являются две пары чисел

и

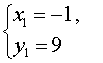
Ответ : (– 1 ; 9) , (9 ; – 1)

Однородные уравнения второй степени с двумя неизвестными

Определение 5 . Однородным уравнением второй степени с двумя неизвестными x и y называют уравнение вида

где a , b , c – заданные числа.

Пример 5 . Решить уравнение

Решение . Для каждого значения y рассмотрим уравнение (8) как квадратное уравнение относительно неизвестного x . Тогда дискриминант D квадратного уравнения (8) будет выражаться по формуле

откуда с помощью формулы для корней квадратного уравнения найдем корни уравнения (8):

Ответ . Решениями уравнения (8) являются все пары чисел вида

( y ; y) или

где y – любое число.

Следствие . Левую часть уравнения (8) можно разложить на множители

Системы из двух уравнений, одно из которых однородное

Системы из двух уравнений, одно из которых однородное, имеют вид

где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .

Пример 6 . Решить систему уравнений

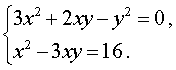(9)

рассматривая его как квадратное уравнение относительно неизвестного x :

.

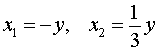
В случае, когда x = – y , из второго уравнения системы (9) получаем уравнение

корнями которого служат числа y₁ = 2 , y₂ = – 2 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 2) , (2 ; – 2) .

,

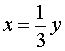
из второго уравнения системы (9) получаем уравнение

которое корней не имеет.

Ответ : (– 2 ; 2) , (2 ; – 2)

Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное

Пример 7 . Решить систему уравнений

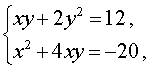(10)

Решение . Совершим над системой (10) следующие преобразования:

• второе уравнение системы оставим без изменений;
• к первому уравнению, умноженному на 5 , прибавим второе уравнение, умноженное на 3 , и запишем полученный результат вместо первого уравнения системы (10).

В результате система (10) преобразуется в равносильную ей систему (11), в которой первое уравнение является однородным уравнением:

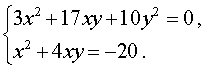(11)

рассматривая его как квадратное уравнение относительно неизвестного x :

.

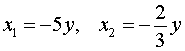
В случае, когда x = – 5y , из второго уравнения системы (11) получаем уравнение

которое корней не имеет.

,

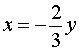
из второго уравнения системы (11) получаем уравнение

,

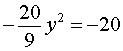
корнями которого служат числа y₁ = 3 , y₂ = – 3 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 3) , (2 ; – 3) .

Ответ : (– 2 ; 3) , (2 ; – 3)

Примеры решения систем уравнений других видов

Пример 8 . Решить систему уравнений (МФТИ)

Решение . Введем новые неизвестные u и v , которые выражаются через x и y по формулам:

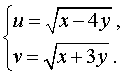(13)

Для того, чтобы переписать систему (12) через новые неизвестные, выразим сначала неизвестные x и y через u и v . Из системы (13) следует, что

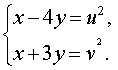(14)

Решим линейную систему (14), исключив из второго уравнения этой системы переменную x . С этой целью совершим над системой (14) следующие преобразования:

• первое уравнение системы оставим без изменений;
• из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.

В результате система (14) преобразуется в равносильную ей систему

из которой находим

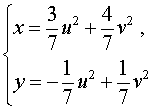(15)

Воспользовавшись формулами (13) и (15), перепишем исходную систему (12) в виде

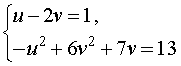(16)

У системы (16) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное u через неизвестное v и подставить это выражение во второе уравнение системы:

Следовательно, решениями системы (16) являются две пары чисел

Из формул (13) вытекает, что 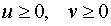, поэтому первое решение должно быть отброшено. В случае u₂ = 5, v₂ = 2 из формул (15) находим значения x и y :

Определение 6 . Решением системы из двух уравнений с тремя неизвестными называют тройку чисел (x ; y ; z) , при подстановке которых в каждое уравнение системы получается верное равенство.

Пример 9 . Решить систему из двух уравнений с тремя неизвестными

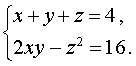(17)

Решение . У системы (17) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное z через неизвестные x и y и подставить это выражение во второе уравнение системы:

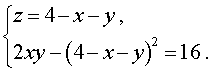(18)

Перепишем второе уравнение системы (18) в другом виде:

Поскольку квадрат любого числа неотрицателен, то выполнение последнего равенства возможно лишь в случае x = 4, y = 4 .

Ответ : (4 ; 4 ; – 4)

Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы линейных уравнений» и нашим учебным пособием «Системы уравнений».

Нелинейные системы уравнений. Рекомендации для старшеклассников

учитель математики высшей категории МКОУ «Любинская СОШ №3»

Решение систем нелинейных уравнений — раздел алгебры считается одним из трудных разделов, так как нет единых способов решения систем алгебраических уравнений, особенно, если речь идет о нелинейных системах уравнений. Так как школьники испытывают затруднения при выполнении такого типа заданий, то возникла идея составить рекомендации для старшеклассников по теме «Нелинейные системы уравнений».

Рассмотрим нелинейную систему уравнений

(, , … ,) = 0

(, , … ,) = 0

(, , … ,) = 0

Где (,, … , ) — рациональные функции (функция (, … , ) называется рациональной, если над переменными , , …, производится лишь операции сложения, вычитания, умножения и деления; всякую рациональную функцию можно после приведения к общему знаменателю представить в виде отношения двух многочленов). Число неизвестных k может не совпадать с числом уравнений n.

Упорядоченная система из K чисел (,, … ,) называется решением системы (I), если при подстановке в уравнения системы вместо переменных соответствующих чисел все уравнения системы превращается в верные равенства.

Решить систему уравнений – значит найти множество всех ее решений.

В этом задании мы рассматриваем системы действительными коэффициентами; параметры, входящие в уравнения, также принимают действительные значения и ищутся лишь действительные решения.

Не всякая нелинейная система уравнений имеет решения. Например, система уравнений

не имеет решений.

Система уравнений, не имеющая решений, называется несовместной.

В 7-м классе мы знакомились с линейными системами (все неизвестные входят в первой степени). В этом случае можно указать общий метод решения линейных систем. Например, метод Гаусса последовательного исключения переменных.

Если же хотя бы одно из неизвестных входит в систему в степени, отличной от 1, то система уже будет нелинейной.

Для решения нелинейных систем уравнений не существует общего метода. Познакомимся на конкретных примерах с некоторыми приёмами, которые часто используются при решении таких систем.

1. Переход к равносильной (более простой) системе

Как правило, при решении систем уравнений мы производим различные преобразования уравнений, входящих в систему; упрощаем выражения, стоящие в левых и правых частях уравнения; переносим слагаемые из одной части в другую; возводим в степень обе части уравнения; складываем соответственные части двух уравнений и т. д. В результате этих преобразований мы последовательно заменяем исходную систему другими системами, всё более простыми, пока не получим систему, которую умеем решать.

Однако на этом пути нас подстерегают две опасности потеря решений и приобретение лишних «решений». Заметим, что появление лишних «решений», в принципе, не опасно, ибо проверкой всегда можно установить, какие решения действительно удовлетворяют исходной системе, а какие являются посторонними и должны быть отброшены. Другое дело – потеря решений. Выше мы говорили, что решить систему уравнений – это найти множество всех ее решений, следовательно, потеря решений недоступна.

Поэтому наибольший интерес представляют те преобразования, которые не приводят ни к потере решений, ни к приобретению лишних «решений». Система, возникающая в результате таких преобразований, называется равносильной исходной системе (другими словами, две системы уравнений называются равносильными, если любое решение первой системы является также решением второй и, наоборот, любое решение второй системы является также решением первой).

Преобразования, приводящие к равносильной системе, будем называть равносильными преобразованиями.

Рассмотрим задачу I. Решить систему уравнений

(2)

Решение. Сложим первое и третье уравнения системы (2)

Умножим первое уравнение на 2 и сложим со вторым

Если теперь в системе (2) заменить первое и третье уравнение на получение, то возникнет новая система, равносильная исходной

(3)

Умножим далее первое уравнение системы (3) на 2 и сложим со вторым; получим уравнение

Система (3) равносильна системе

(4)

Из первого уравнения системы (4) находим два значения x:

Подставляя значения в последние два уравнения системы (4), получим для определения y и z систему

которая имеет решения z=-1, y=-3; z=-1,y=1. Итак, при, мы нашли два решения системы (4), а значит, в силу равносильности, и исходной системы (2): (2,-3,-1), (2,1,-1).

Аналогично при получим еще четыре решения системы (2): (3,2,-3);(3,2,1);(3,-4,-3);(3,-4,+1).

Основные равносильные преобразования, которые часто применяются при решении нелинейных систем и наиболее характерные случаи, когда нарушается равносильность преобразований.

К равносильным преобразованиям относятся:

1) прибавление к обеим частям некоторого уравнения системы выражения, которое не изменяет область допустимых значений всех переменных, входящих в систему (областью допустимых значений переменных называется совокупность всех значений переменных, при которых и левые и правые части всех уравнений, входящих в систему, имеют смысл):

2) приведение подобных членов, если при этом не меняется область допустимых значений переменных:

3) умножение обеих частей уравнения на некоторое выражение, которое не изменяет область допустимых значений переменных и не обращается в нуль в этой области (в частности, обе части уравнения можно умножать на число, отличное от нуля);

4) замена некоторого уравнения системы уравнением, которое получается следующим образом: обе части указанного уравнения умножаем на число, отличное от нуля, и прибавляем к ним соответствующие части другого уравнения системы, предварительно умножение на произвольное число.

Случаи, когда нарушается равносильность

1) возведение в квадрат (в четную степень) обеих частей какого-нибудь уравнения системы; могут появиться посторонние «решения», нужна проверка; 2) деление (умножение) обеих частей некоторого уравнения на выражение, которое может обращаться в нуль в области допустимых значений переменных; это может привести как к потери решений, так и к приобретению лишних «решений»; 3) сокращение дроби, входящей в некоторое уравнение, на общий множитель, если этот множитель может обратиться в нуль в области допустимых значений переменных; могут появиться посторонние «решения», нужна проверка.

Важно также отметить, что равносильность может нарушиться, если в результате некоторого преобразования изменяется область допустимых значений переменных. При этом надо иметь в виду, что если область допустимых значений расширилась — могут появиться посторонние решения, если же сузилась – могут быть утеряны решения.

Все сказанное в равной мере относится и к уравнениям, и к системам уравнений (не обязательно нелинейных).

Доказательства приведенных выше утверждений можно найти, например, в книгах и , гл. 9, 1,2, гл. 10, 1 (мы же в целях краткости ограничились лишь конспективным изложением этих важных вопросов).

2. Разложение на множители

Если какое-нибудь уравнение системы удается разложить на множители, то система распадается на несколько более простых систем. Например, в системе (5)

левая часть первого уравнения легко разлагается на множители: . Соответственно, система (5) распадается на две системы: 1. 2. (6)

Система (5) равносильна совокупности систем (6.1) и (6.2) . Это означает следующее: любое решение системы 5 является решением хотя бы одной из систем (6) является решением системы (5). Поэтому, для решения системы (5) достаточно решить более простые системы(6).

Решим указанным способом более сложную задачу.

Задача 2 . Решить систему

Решение. По смыслу задачи xyz ≠0

Почленно складывая все три уравнения системы, и заменяя первое уравнение системы полученным, перейдем к равносильной системе

Которая распадается на две системы:

1. 2.

Рассмотрим первую из этих систем. Разделим второе уравнение этой системы на x, третье – на у, приравняем левые части полученных уравнений; получим систему, равносильную системе 1:

(8)

Преобразуем первое уравнение системы (8), учитывая второе уравнение этой же системы и условие (7):

,

Отсюда, так как x + y = —z , следует, что z = 0, а это противоречит условию

(7) . Таким образом, система 1 решений не имеет. Рассмотрим систему 2 . Из первого уравнения находим

,

Используя эти соотношения, легко получаем из второго и третьего уравнений, что ,

Система 2 равносильна системе

Эта последняя система легко решается. Вот её решения:

( 2, 2, 2), (2, -2, -2), (-2, 2, -2), (-2, -2,

Следовательно, решения (9) , и только они, будут решениями исходной системы.

3. Метод замены неизвестных

Этот метод является одним из основных при решении систем.

а) Проиллюстрируем его применение на конкретной задаче.

Решение. Сделаем замену переменных

X y = 4, x y = v, y z = v

В результате указанной замены получим систему:

Из первого уравнения этой системы находим , из третьего —

Подставляя во второе уравнения вместо v и w их выражения через u, получим

Это уравнение легко сводится к квадратному и имеет корни: u=1, u=-1. При u=1 находим v2, w4; при u1 находим v8, w=-2

Итак, мы должны теперь решить две системы:

1. 2.

Решив их, найдём решения исходной системы:

При решении системы трех уравнений и относительно

Мы применили метод исключения неизвестных. Суть этого метода ясна из решения указанной системы.

В общем случае нельзя заранее указать, какие именно замены неизвестных следует сделать при решении той или иной системы. Такие указания можно дать лишь относительно систем специального вида.

Б) При решении системы, симметричной относительно х и у (система называется симметричной относительно х и у, если она не изменяется при перестановке х и у местами) часто бывает удобна замена

U = x + y, v = x y (10)

Задача 4. Найти действительные решения системы

Решение. Данная система симметрична относительно х и у.

Сделав замену ( 10 ) , придем к системе

Складывая уравнения этой системы, получим квадратное уравнение относительно u: u+ u – 12 = 0, которое имеет решения u= -4, u= 3. При u= -4 имеем v= 9, при u= 3, соответственно v= 2.

Теперь нам надо решить две системы:

Нетрудно видеть, что первая из этих систем не имеет действительных решений, а вторая система имеет решения (1,2), (2,1).

Соответственно, исходная система имеет решения .

в) При решении системы из трех уравнений, симметричной относительно x, y, z замена

x+y+z=u, xy+yz+xz=v, xyz=w

как правило, ведет к упрощению исходной системы. После такой замены, решив более простую систему относительно u, v, w необходимо для нахождения неизвестных x, y, z решить систему вида

(11)

Исключив два неизвестных (например, x и y) получим относительно z кубическое уравнение. Если удастся его решить, то не составляет труда довести до конца решение системы (11).

4. Однородные системы двух уравнений второй степени с двумя неизвестными.

Так называются системы вида

(12)

Решаются они следующим образом. Вначале найдем решения, отвечающие y=0 (если они есть; нахождение таких решений не составляет труда). Предположим затем, что

(13)

Далее рассмотрим следующие случаи.

а) Умножим первое уравнение системы (12) на , второе – на — и сложим полученные уравнения:

и перепишем это уравнение в виде

Разделим обе части этого уравнения на (см. условие (13)) в результате получим равносильное уравнение

(14)

Решив полученное квадратное уравнение относительно , легко довести до конца решение исходной системы (12).

б) (или )

В этом случае правая часть одного из уравнений системы (12) уже равна нулю и можно, предполагая (13), сразу делить обе части этого уравнения на . Снова придем к уравнению вида (14).

Задача 5. Решить систему.

Очевидно, что при система решений не имеет. Пусть . Умножим первое уравнение на 7, второе – на -3 и сложим полученные уравнения:

Разделив на , придем к уравнению

,

,

Пусть вначале . Исключив из первого уравнения исходной системы, найдем , откуда . Это дает два решения исходной системы: (2,1), (-2,-1).

Пусть теперь . Исключим ; получим уравнение , откуда . Это дает еще два решения исходной системы: , .

5. Системы с параметрами

Очень интересны системы с параметрами (буквенными коэффициентами). Здесь всегда следует помнить, что мы имеем дело с бесконечным числом систем уравнений, т. к. буквенный коэффициент может принимать любое действительное значение. Поэтому, чтобы решить систему с параметром, всегда необходимо проводить исследование. Основной задачей исследования является указание области значений параметра, в которой данная система имеет решение. В случае необходимости в исследование включается разбиение области значений параметра на несколько областей, для которых исходная система имеет различные решения. Разберем задачу.

Задача 6. Найти действительные решения системы.

Решение. По смыслу задачи , . Умножим обе части первого уравнения на :

Следовательно, исходная система распадается на две системы:

1. 2.

Рассмотрим каждую из этих систем отдельно.

1. Очевидно, что система 1 имеет единственное решение

Это решение является также решением исходной системы лишь при , ибо если , то .

2. Использую второе уравнение, получим

При система решений не имеет. Пусть

Следовательно, и являются корнями квадратного уравнения

Решим это квадратное уравнение:

Найдем значения , при которых дискриминант неотрицателен:

Отсюда находим: либо . Таким образом, при и система 2 имеет два решения

; ;

а при — одно решение

Заметим, что это решение нами было уже найдено.

Ответ. При система несовместна;

при система имеет одно решение

при и система имеет три решения

, ,

Разберем еще одну задачу.

Задача 7. При каких значениях система

имеет единственное решение? Найти это решение.

Решение. Из второго уравнения имеем

Подставив это значение в первое уравнение, получим

Дополним выражения в скобках до полных квадратов

(15)

Если , то уравнение (15) в области действительных чисел не имеет решений, следовательно, исходная система при этих значениях несовместна. Если , то уравнение (15) определяет на плоскости окружность с центром в точке радиуса (см. рис.)

Очевидно, что координаты любой точки, лежащей на окружности, удовлетворяют уравнению (15). Соответственно, исходная система имеет в этом случае бесконечно много решений.

Пусть, наконец, . В этом случае уравнение (15) определяет единственную точку . В этом случае и исходная система имеет единственное решение. Итак, система имеет единственное решение при .

При единственным решением будет , а при — соответственно, .

6. Иррациональные системы

В заключение рассмотрим иррациональные системы. Так называются системы, в которых неизвестные могут входить под знаком радикала.

Чтобы решить такую систему, следует либо заменой, либо возведением в подходящую степень избавиться от радикалов. Таким образом переходят к нелинейной системе, которую решают вышеописанным способами.

При этом надо иметь в виду следующие обстоятельства (ниже речь идет лишь о действительных числах и действительных решениях систем):

1) в случае корней четной степени рассматриваются выражение неотрицательно; при этом берется только неотрицательное значение корня. В частности, .

2) в случае корней нечетной степени подкоренное выражение может быть любым вещественным числом (в этом случае знак корня совпадает со знаком подкоренного выражения).

3) при воздействии обеих частей некоторого уравнения в квадрат (четную запись) могут появиться лишние корни. В этом случае нужна проверка.

4) Рассмотрим в качестве примера две задачи.

Задача 8. Решить систему

Решение. Возведем обе части первого уравнения в квадрат и в полученном уравнении подставим из второго уравнения. В результате будем иметь

(16)

Возведем еще раз обе части уравнения в квадрат, получим

,

Отсюда находим, и .

Первое значение отбрасываем, т. к. уравнение (16) имеет смысл лишь при отрицательном значении . Итак, .

(17)

Очевидно, что все решения исходной системы содержатся среди решений системы (17). Система (17) имеет решения . Проверка показывает, что исходной системе удовлетворяет лишь одно решение .

Ответ. .

Задача 9. Найти действительные решения системы

Решение. Сделаем замену .

Относительно и получим следующую систему

или

Отсюда находим ; и, окончательно, ; .

1. Ответ.

2. , Элементарная алгебра (дополнительный курс).

1. Лодочник проплыл в лодке по течению реки расстояние от А до В и затем вернулся обратно в пункт А. Выяснилось, что против течения лодочник плыл на ч. больше, чем по течению. Определить скорость, с какой бы он плыл в стоячей воде, если известно, что за 3 ч. лодочник проплыл по течению реки столько же километров, сколько за 7 ч. пролив течения. Расстояние от А до В 21 км.

Найти действительные решения систем:

2.

3.

4.

5.

6.

7.

8. Доказать, что система

в области действительных чисел несовместна.

Найти действительные решения систем:

9.

10.

11.

12.

13.

14.

Нелинейные уравнения и системы уравнений. Методы их решения.

Нелинейные уравнения и системы уравнений. Методы их решения.

Одной из важных задач прикладной математики является задача решения нелинейных уравнений, встречающихся в разных областях научных исследований.

Под нелинейными уравнениями ( nonlinear equations ) понимаются алгебраические и трансцендентные уравнения с одним неизвестным в следующем виде:

,

где — действительное число, — нелинейная функция.

Под системой нелинейных уравнений понимается система алгебраических и трансцендентных уравнений в следующем виде:

где < > — действительные числа, < … > — нелинейные функции.

Алгебраическое уравнение — это уравнение содержащие только алгебраические функции, которое можно представить многочленом n ‐ ой степени с действительными коэффициентами (целые, рациональные, иррациональные) в следующем виде:

.

Трансцендентное уравнение – это уравнение содержащие в своем составе функции, которые являются не алгебраическими. Простейшими примерами таких функций служат показательная функция, тригонометрическая функция, логарифмическая функция и т.д.

Решением нелинейного уравнения (или системы нелинейных уравнений) называют совокупность (группа) чисел , которые, будучи подставлены на место неизвестных , обращают каждое уравнение (или систему уравнений) в тождество:

.

Для решения нелинейных уравнений (или систем нелинейных уравнений) существует несколько методов решения: графические, аналитические и численные методы.

Графические методы наименее точны, но позволяют в сложных уравнениях определить наиболее приближенные значения, с которых в дальнейшем можно начинать находить более точные решения уравнений.

Аналитические методы (или прямые методы) позволяют определить точные значения решения уравнений. Данный метод позволяет записать корни в виде некоторого соотношения (формул). Подобные методы развиты для решения простейших тригонометрических, логарифмических, показательных, а также алгебраических уравнений. Однако подавляющее большинство нелинейных уравнений, встречающихся на практике, не удается решить прямыми методами. В таких случаях обращаются к численным методам, позволяющим получить приближенное значение корня с любой заданной точностью .

Численные методы решения нелинейных уравнений – это итерационный процесс расчета, который состоит в последовательном уточнении начального приближения значений корней уравнения (системы уравнений). При численном подходе задача о решении нелинейных уравнений разбивается на два этапа:

— локализация (отделение) корней

› Под локализацией корней понимается процесс отыскания приближенного значения корня или нахождение таких отрезков, в пределах которых содержится единственное решение

› Под уточнением корней понимается процесс вычисления приближенных значений корней с заданной точностью по любому численному методу решения нелинейных уравнений.

Недостатком почти всех итерационных методов нахождения корней является то, что они при однократном применении позволяют найти лишь один корень функции, к тому же, мы не знаем какой именно. В случае повторения итерационного процесса при изменении стартовых точек отсутствуют гарантии, что найдется новый корень уравнения, так как итерационный процесс может сойтись к найденному корню.

Для поиска других корней используется метод удаления корней. Данный метод основан на принципе создания новой функции путем деление основной функции на найденный корень уравнения:

.

Так, например, если — корень функции то, чтобы произвести удаление найденного корня и поиск оставшихся корней исходной функции необходимо создать функцию . Точка будет являться корнем функции на единицу меньшей кратности, чем , при этом все остальные корни у функций и совпадают с учетом кратности. Повторяя указанную процедуру, можно найти все корни с учетом кратности.

Следует обратить внимание, что когда производим деление на тот или иной корень , то в действительности мы делим лишь на найденное приближение , и, тем самым, несколько сдвигаем корни вспомогательной функции относительно истинных корней функции . Это может привести к значительным погрешностям, если процедура отделения применялась уже достаточное число раз. Чтобы избежать этого, с помощью вспомогательных функций вычисляются лишь первые итерации, а окончательные проводятся по исходной функции , используя в качестве стартового приближения, последнюю итерацию, полученную по вспомогательной функции.

Локализация корней.

› Локализация корней аналитическим способом

Для отделения корней уравнения необходимо иметь критерий, позволяющий убедится, что, во-первых, на рассматриваемом отрезке имеется корень, а, во-вторых, что этот корень единственный на указанном отрезке. Если функция непрерывна на отрезке , а на концах отрезка её значения имеют разные знаки , то на этом отрезке расположен, по крайней мере, один корень. Дополнительным условием, обеспечивающем единственность корня на отрезке является требование монотонности функции на этом отрезке. В качестве признака монотонности функции можно воспользоваться условием знакопостоянства первой производной . Таким образом, если на отрезке функция непрерывна и монотонна, а ее значения на концах отрезка имеют разные знаки, то на рассматриваемом отрезке существует один и только один корень.

› Локализация корней табличным способом

Допустим, что все интересующие нас корни уравнения находятся на отрезке . Выбор этого отрезка (интервала поиска корней) может быть сделан, например, на основе анализа конкретной физической или иной задачи. Будем вычислять значения , начиная с точки , двигаясь вправо с некоторым шагом h . Как только обнаруживается пара соседних значений , имеющих разные знаки, так соответствующие значения аргумента x можно считать границами отрезка, содержащего корень.

Надежность рассмотренного подхода к отделению корней уравнений зависит как от характера функции , так и от выбранной величины шага h. Действительно, если при достаточно малом значении h ( ) на границах текущего отрезка функция принимает значения одного знака, то естественно ожидать, что уравнение корней на этом отрезке не имеет. Однако, это не всегда так: при несоблюдении условия монотонности функции на отрезке могут оказаться корни уравнения (рис. 1, а). Также несколько корней на отрезке могут оказаться и при выполнении условия (рис. 1, б). Предвидя подобные ситуации, следует выбирать достаточно малые значения h .

Рис. 1. Варианты поведения функции на интервале локализации корня

Поскольку данный способ предполагает выполнение лишь элементарных арифметических и логических операций, количество которых может быть велико при малых значениях h , для его реализации целесообразно использовать вычислительные возможности компьютера.

Отделяя, таким образом, корни, мы, по сути, получаем их приближенные значения с точностью до выбранного шага. Так, например, если в качестве приближенного значения корня взять середину отрезка локализации, то абсолютная погрешность этого значения не будет превосходить половины шага поиска ( h /2). Уменьшая шаг в окрестности каждого корня, можно, в принципе, повысить точность отделения корней до любого наперед заданного значения. Однако такой способ требует большого объема вычислений. Поэтому при проведении численных экспериментов с варьированием параметров задачи, когда приходится многократно осуществлять поиск корней, подобный метод не годится для уточнения корней и используется только для отделения (локализации) корней, т.е. определения начальных приближений к ним. Уточнение корней проводится с помощью других, более экономичных методов.

Уточнение корней.

На данном этапе задача состоит в получении приближенного значения корня, принадлежащего отрезку , с заданной точностью (погрешностью) e . Это означает, что вычисленное значение корня должно отличаться от точного не более чем на величину e :

Существует большое количество численных методов решения нелинейных уравнений для уточнения корней, которые условно можно разделить:

› Методы решение уравнений с одним неизвестным. Основными представителями являются:

— метод половинного деления;

— метод простой итерации;

— метод Ньютона для уравнения с одним неизвестным;