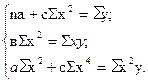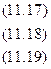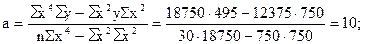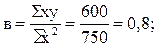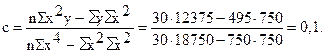Уравнение параболической регрессии
В некоторых случаях эмпирические данные статистической совокупности, изображенные наглядно с помощью координатной диаграммы, показывают, что увеличение фактора сопровождаются опережающим ростом результата. Для теоретического описания такого рода корреляционной взаимосвязи признаков можно взять уравнение параболической регрессии второго порядка:
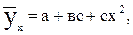
где 

Положив в основу вычисления параметров 

Из этих уравнений можно найти параметры 

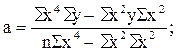
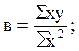
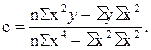
Отсюда видно, что для определения параметров 

Допустим, имеются данные об удельном весе посевов картофеля в структуре всех посевных площадей и урожае (валовом сборе) культуры в 30 сельскохозяйственных организациях. Необходимо составить и решить уравнение корреляционной взаимосвязи между этими показателями.
Т а б л и ц а 11.9. Расчет вспомогательных показателей для уравнения
Параболической регрессии
| № п.п. | х | у | ху | х 2 | х 2 у | х 4 |
| х1 | у1 | х1у1 | 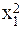 | 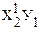 | 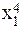 | |
| х2 | у2 | х2у2 | 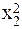 | 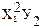 | 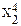 | |
| … | … | … | … | … | … | … |
| n | хn | уn | хnуn | 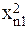 | 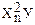 | 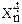 |
| Σ | Σх | Σу | Σху | Σх 2 | Σх 2 у | Σх 4 |
Графическое изображение поля корреляции показало, что изучаемые показатели эмпирически связаны между собой линией, приближающейся к параболе второго порядка. Поэтому расчет необходимых параметров 

Т а б л и ц а 11.10. Расчет вспомогательных данных для уравнения
Параболической регрессии
| № п.п. | х, % | у, тыс.т | ху | х 2 | х 2 у | х 4 |
| 1,0 | 5,0 | 5,0 | 1,0 | 5,0 | 1,0 | |
| 1,5 | 7,0 | 10,5 | 2,3 | 15,8 | 5,0 | |
| … | … | … | … | … | … | … |
| n | 8,0 | 20,0 | 160,0 | 64,0 | ||
| Σ |
Подставим конкретные значения Σ у=495, Σ ху=600, Σ х 2 =750, Σ х 2 у=12375, Σ х 4 =18750, имеющиеся в табл. 11.10, в формулы (11.20), (11.21), (11.22). Получим
Таким образом, уравнение параболической регрессии, выражающие влияние удельного веса посевов картофеля в структуре посевных площадей на урожай (валовой сбор) культуры в сельскохозяйственных организациях, имеет следующий вид:
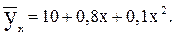
Уравнение 11.23 показывает, что в условиях заданной выборочной совокупности средний урожай (валовой сбор) картофеля (10 тыс. ц) может быть получен без влияния изучаемого фактора – повышения удельного веса посевов культуры в структуре посевных площадей, т.е. при таком условии, когда колебания удельного веса посевов не будут оказывать воздействие на размер урожая картофеля (х=0). Параметр (коэффициент пропорциональности) в=0,8 показывает, что каждый процент повышения удельного веса посевов обеспечивает прирост урожая в среднем на 0,8 тыс. т, а параметр с=0,1 свидетельствует о том, что на один процент (в квадрате) ускоряется приращение урожая в среднем на 0,1 тыс. т картофеля.
Параболическая регрессия
Уравнение параболической регрессии имеет вид

Если использовать метод наименьших квадратов (МНК), то для коэффициентов составляется и решается нормальная система линейных уравнений с матрицей
Входящие сюда величины подсчитываются по данным наблюдений.
Левая часть – это средние значения различных степеней фактора Х. Правая – это средние значения произведений:

Посчитывая эти числа и решая систему уравнений, находим коэффициенты регрессии.
Рекомендуемые файлы
Можно подсчитывать каждую из этих величин в отдельности. Но можно применить для этого и другой способ, матричный. При этом вся матрица коэффициентов системы подсчитывается сразу.
Для этого сначала нужно сформировать исходные данные в виде матриц
Для фактора Х эта матрица состоит из трех столбцов:
¨ столбец собственно Х;
Здесь величины записаны точно так же, как и в уравнении регрессии:
Теперь исходные данные собраны в двух матрицах. Это матрица X. и матрица Y.
Матрица нормальной системы вычисляется произведением матриц
где 
Столбец правых частей нормальной системы вычисляется как произведение матриц
Если и неизвестные коэффициенты сформировать в матрицу
то сама система тоже может быть записана в матричном виде.

Но тогда естественно и решение получить в матричной записи, в виде обратной матрицы:
Если строить уравнение регрессии в виде многочлена
и при этом использовать матричный способ составления и решения нормальной системы, то формулы нисколько не изменятся, только матрица Х исходных данных будет содержать уже n столбцов.
Проверка адекватности квадратичного уравнения регрессии
Проводится по критерию Фишера
Проводится сравнение двух дисперсий: исправленной дисперсии фактора Y и дисперсии остатков
· исправленная дисперсию Y :
· дисперсия остатков: 

Подсчитанной наблюдаемое значение критерия Фишера сравниваем с найденным из таблиц критическим значением. Для пользования таблицами задаем уровень значимости и числа степеней свободы:
Чем больше F набл по сравнению с F кр , тем выше адекватность . Сравнивая, делаем вывод об адекватности (или неадекватности) построенной корреляционной модели причем оцениваем и степень адекватности.
ИНСТРУКЦИЯ К ЛАБОРАТОРОЙ РАБОТЕ
Анализ монопольного рынка
Имеются статистические данные для цены P и для спроса D на монопольный товар. Требуется рассчитать оптимальные цены, при которых
будут максимальными доход или прибыль.
Если описать зависимость спроса D от цены P теоретической формулой D(P), то с помощью этой теоретической зависимости можно будет исследовать зависимость дохода Z и прибыли F от цены P .
Тогда величина дохода Z равна произведению цены P на объем реализованного спроса:
В свою очередь, издержки G состоят из постоянных (C) и переменных затрат (V·D), которые пропорциональны объему произведенной продукции (V – затраты на единицу продукции):
Таким образом, для прибыли получаем формулу:
Чтобы найти величину цены, при которой максимальны доход или прибыль, нужно взять производную от них по цене P приравнять ее нулю:
Решая эти квадратные уравнения и выбирая из двух корней то значение, которое соответствует максимуму, находим значение цены, при которой максимальны доход или прибыль.
Рассмотрим также величину, называемую коэффициентом эластичности спроса:

Это число показывает, на сколько процентов изменяется спрос D при росте цены на 1% .
Так как цена P и спрос D всегда положительны, знак K d определяется знаком производной. Для подавляющего большинства товаров спрос падает с ростом цены, и значит производная D ′ p отрицательна. А значит, отрицательным будет и коэффициент эластичности.
Существует такое понятие, как эластичность и неэластичность спроса. При этом характер спроса определяется реакцией дохода на изменение цены.

¨ спрос неэластичен, если с ростом цены доход тоже растет;
Рост или убывание дохода определяется знаком производной 
В зависимости от величины коэффициента эластичности K d
возможны следующие случаи:
1. 


2. 


· В ячейки AQ23 и AQ24 занести значения постоянных затрат C и переменных затрат V из вашего варианта исходных данных (дать ячейкам имена).
· Построить графики полученных зависимостей (Мастер диаграмм, Точечная диаграмма с последующим редактированием):
¨ На одном графике совместить зависимость дохода, издержек и прибыли от цены.
вать график, чтобы он выглядел следующим образом:
5 видов регрессии и их свойства
Линейная и логистическая регрессии обычно являются первыми видами регрессии, которые изучают в таких областях, как машинное обучение и наука о данных. Оба метода считаются эффективными, так как их легко понять и использовать. Однако, такая простота также имеет несколько недостатков, и во многих случаях лучше выбирать другую регрессионную модель. Существует множество видов регрессии, каждый из которых имеет свои достоинства и недостатки.
Мы познакомимся с 7 наиболее распространенными алгоритмами регрессии и опишем их свойства. Также мы узнаем, в каких ситуация и с какими видами данных лучше использовать тот или иной алгоритм. В конце мы расскажем о некоторых инструментах для построения регрессии и поможем лучше разобраться в регрессионных моделях в целом!
Линейная регрессия
Регрессия — это метод, используемый для моделирования и анализа отношений между переменными, а также для того, чтобы увидеть, как эти переменные вместе влияют на получение определенного результата. Линейная регрессия относится к такому виду регрессионной модели, который состоит из взаимосвязанных переменных. Начнем с простого. Парная (простая) линейная регрессия — это модель, позволяющая моделировать взаимосвязь между значениями одной входной независимой и одной выходной зависимой переменными с помощью линейной модели, например, прямой.
Более распространенной моделью является множественная линейная регрессия, которая предполагает установление линейной зависимости между множеством входных независимых и одной выходной зависимой переменных. Такая модель остается линейной по той причине, что выход является линейной комбинацией входных переменных. Мы можем построить модель множественной линейной регрессии следующим образом:
Y = a_1*X_1 + a_2*X_2 + a_3*X_3 ……. a_n*X_n + b
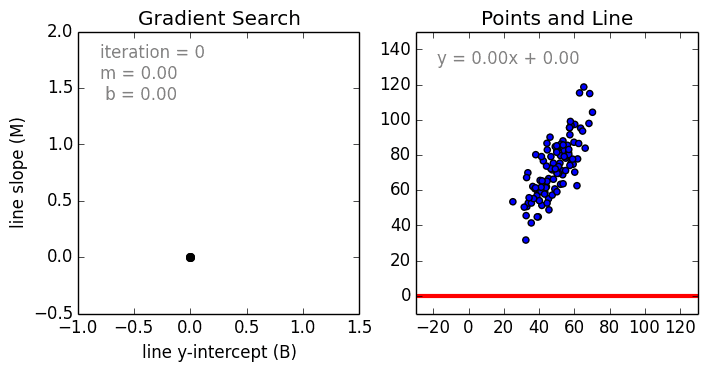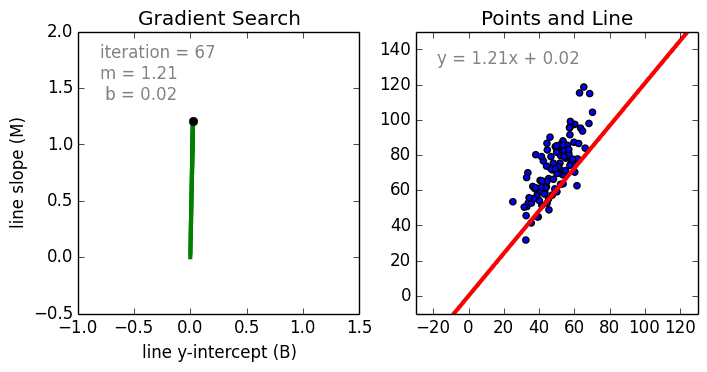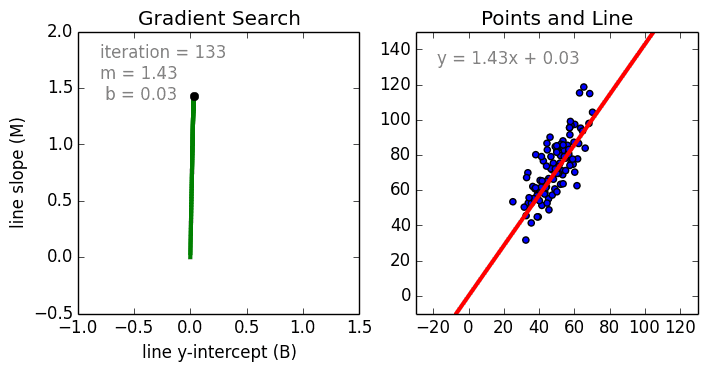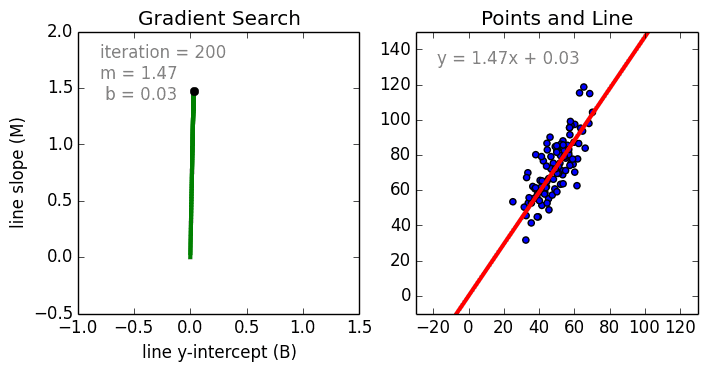
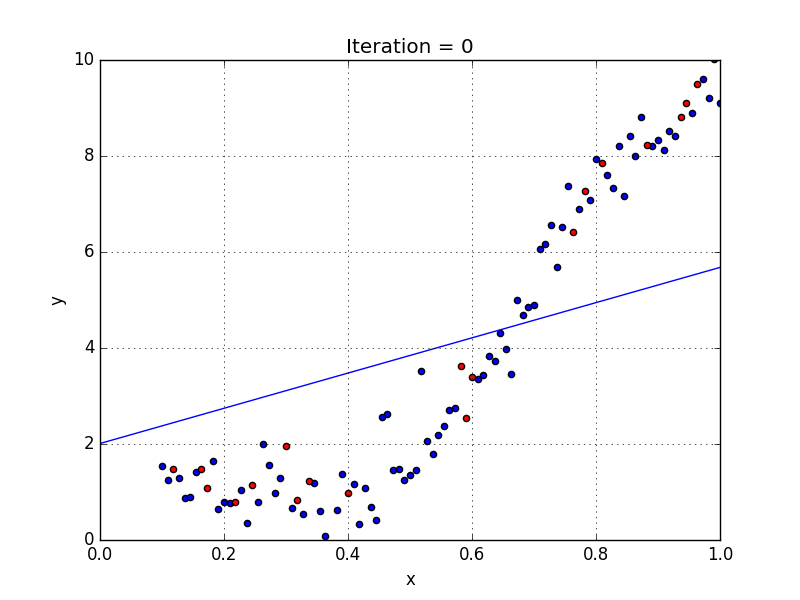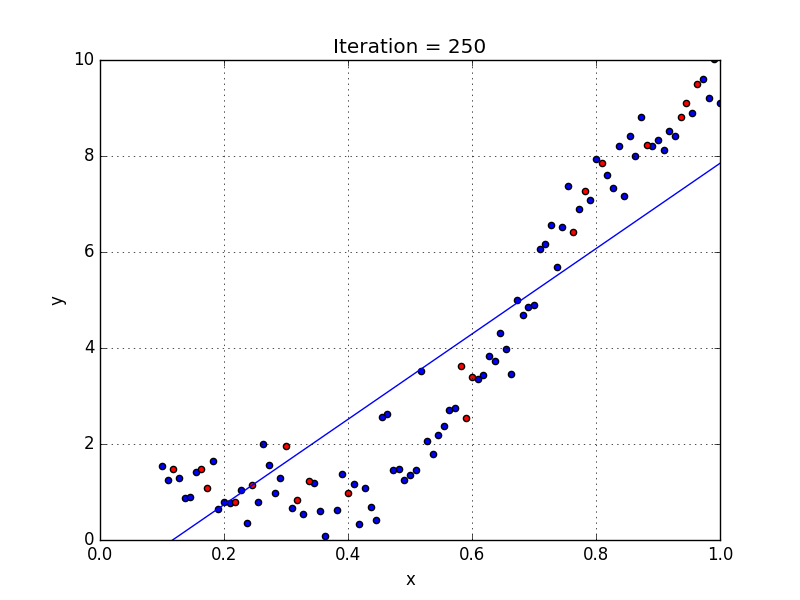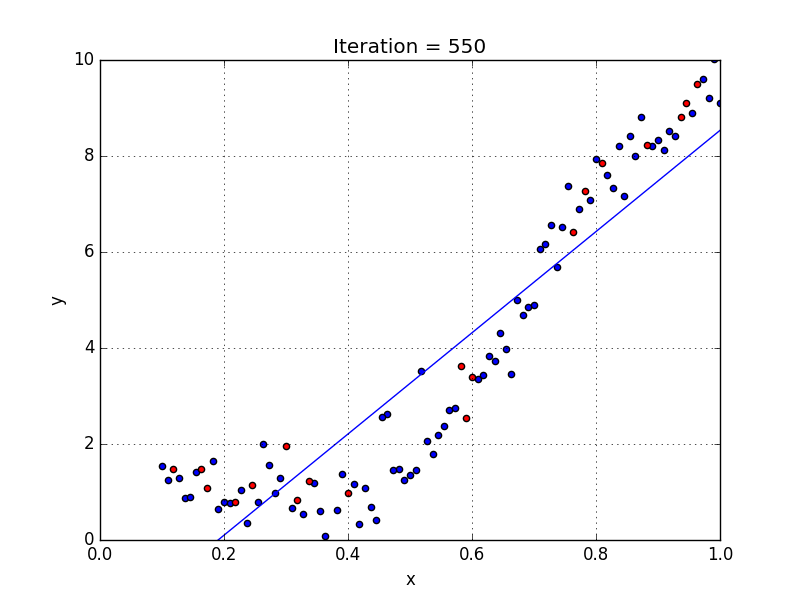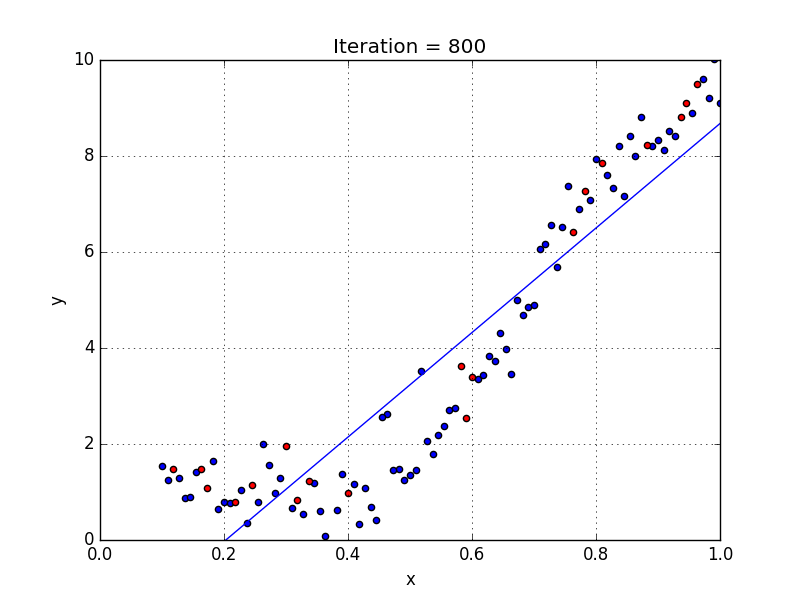
Где a_n — это коэффициенты, X_n — переменные и b — смещение . Как видим, данная функция не содержит нелинейных коэффициентов и, таким образом, подходит только для моделирования линейных сепарабельных данных. Все очень просто: мы взвешиваем значение каждой переменной X_n с помощью весового коэффициента a_n. Данные весовые коэффициенты a_n, а также смещение b вычисляются с применением стохастического градиентного спуска. Посмотрите на график ниже в качестве иллюстрации!
Несколько важных пунктов о линейной регрессии:
- Она легко моделируется и является особенно полезной при создании не очень сложной зависимости, а также при небольшом количестве данных.
- Обозначения интуитивно-понятны.
- Чувствительна к выбросам.
Полиномиальная регрессия
Для создания такой модели, которая подойдет для нелинейно разделяемых данных, можно использовать полиномиальную регрессию. В данном методе проводится кривая линия, зависимая от точек плоскости. В полиномиальной регрессии степень некоторых независимых переменных превышает 1. Например, получится что-то подобное:
Y = a_1*X_1 + (a_2)²*X_2 + (a_3)⁴*X_3 ……. a_n*X_n + b
У некоторых переменных есть степень, у других — нет. Также можно выбрать определенную степень для каждой переменной, но для этого необходимы определенные знания о том, как входные данные связаны с выходными. Сравните линейную и полиномиальную регрессии ниже.
Несколько важных пунктов о полиномиальной регрессии:
- Моделирует нелинейно разделенные данные (чего не может линейная регрессия). Она более гибкая и может моделировать сложные взаимосвязи.
- Полный контроль над моделированием переменных объекта (выбор степени).
- Необходимо внимательно создавать модель. Необходимо обладать некоторыми знаниями о данных, для выбора наиболее подходящей степени.
- При неправильном выборе степени, данная модель может быть перенасыщена.
Гребневая (ридж) регрессия
В случае высокой коллинеарности переменных стандартная линейная и полиномиальная регрессии становятся неэффективными. Коллинеарность — это отношение независимых переменных, близкое к линейному. Наличие высокой коллинеарности можно определить несколькими путями:
- Коэффициент регрессии не важен, несмотря на то, что, теоретически, переменная должна иметь высокую корреляцию с Y.
- При добавлении или удалении переменной из матрицы X, коэффициент регрессии сильно изменяется.
- Переменные матрицы X имеют высокие попарные корреляции (посмотрите корреляционную матрицу).
Сначала можно посмотреть на функцию оптимизации стандартной линейной регрессии для лучшего понимания того, как может помочь гребневая регрессия:
Где X — это матрица переменных, w — веса, y — достоверные данные. Гребневая регрессия — это корректирующая мера для снижения коллинеарности среди предикторных переменных в регрессионной модели. Коллинеарность — это явление, в котором одна переменная во множественной регрессионной модели может быть предсказано линейно, исходя из остальных свойств со значительной степенью точности. Таким образом, из-за высокой корреляции переменных, конечная регрессионная модель сведена к минимальным пределам приближенного значения, то есть она обладает высокой дисперсией.
Гребневая регрессия добавляет небольшой фактор квадратичного смещения для уменьшения дисперсии:
min || Xw — y ||² + z|| w ||²
Такой фактор смещения выводит коэффициенты переменных из строгих ограничений, вводя в модель небольшое смещение, но при этом значительно снижая дисперсию.
Несколько важных пунктов о гребневой регрессии:
- Допущения данной регрессии такие же, как и в методе наименьших квадратов, кроме того факта, что нормальное распределение в гребневой регрессии не предполагается.
- Это уменьшает значение коэффициентов, оставляя их ненулевыми, что предполагает отсутствие отбора признаков.
Регрессия по методу «лассо»
В регрессии лассо, как и в гребневой, мы добавляем условие смещения в функцию оптимизации для того, чтобы уменьшить коллинеарность и, следовательно, дисперсию модели. Но вместо квадратичного смещения, мы используем смещение абсолютного значения:
min || Xw — y ||² + z|| w ||
Существует несколько различий между гребневой регрессией и лассо, которые восстанавливают различия в свойствах регуляризаций L2 и L1:
- Встроенный отбор признаков — считается полезным свойством, которое есть в норме L1, но отсутствует в норме L2. Отбор признаков является результатом нормы L1, которая производит разреженные коэффициенты. Например, предположим, что модель имеет 100 коэффициентов, но лишь 10 из них имеют коэффициенты отличные от нуля. Соответственно, «остальные 90 предикторов являются бесполезными в прогнозировании искомого значения». Норма L2 производит неразряженные коэффициенты и не может производить отбор признаков. Таким образом, можно сказать, что регрессия лассо производит «выбор параметров», так как не выбранные переменные будут иметь общий вес, равный 0.
- Разряженность означает, что незначительное количество входных данных в матрице (или векторе) имеют значение, отличное от нуля. Норма L1 производит большое количество коэффициентов с нулевым значением или очень малые значения с некоторыми большими коэффициентами. Это связано с предыдущим пунктом, в котором указано, что лассо исполняет выбор свойств.
- Вычислительная эффективность: норма L1 не имеет аналитического решения в отличие от нормы L2. Это позволяет эффективно вычислять решения нормы L2. Однако, решения нормы L1 не обладают свойствами разряженности, что позволяет использовать их с разряженными алгоритмами для более эффективных вычислений.
Регрессия «эластичная сеть»
Эластичная сеть — это гибрид методов регрессии лассо и гребневой регрессии. Она использует как L1, так и L2 регуляризации, учитывая эффективность обоих методов.
min || Xw — y ||² + z_1|| w || + z_2|| w ||²
Практическим преимуществом использования регрессии лассо и гребневой регрессии является то, что это позволяет эластичной сети наследовать некоторую стабильность гребневой регрессии при вращении.
Несколько важных пунктов о регрессии эластичной сети:
- Она создает условия для группового эффекта при высокой корреляции переменных, а не обнуляет некоторые из них, как метод лассо.
- Нет ограничений по количеству выбранных переменных.
Вывод
Вот и все! 5 распространенных видов регрессии и их свойства. Все данные методы регуляризации регрессии (лассо, гребневая и эластичной сети) хорошо функционирует при высокой размерности и мультиколлинеарности среди переменных в наборе данных.
http://studizba.com/lectures/139-jekonomika-i-finansy/2256-lekcii-po-jekonometrike/43041-10-parabolicheskaja-regressija.html
http://medium.com/nuances-of-programming/5-%D0%B2%D0%B8%D0%B4%D0%BE%D0%B2-%D1%80%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D0%B8-%D0%B8-%D0%B8%D1%85-%D1%81%D0%B2%D0%BE%D0%B9%D1%81%D1%82%D0%B2%D0%B0-f1bb867aebcb