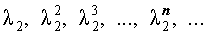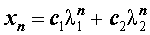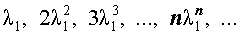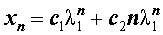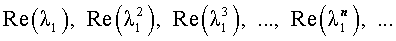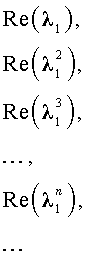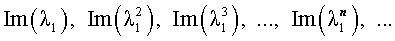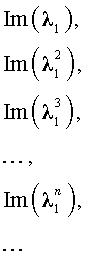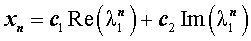Возвратные последовательности:
рекуррентная формула, характеристическое уравнение
 Определение возвратной последовательности Определение возвратной последовательности |
 Характеристическое уравнение Характеристическое уравнение |
 Общее решение рекуррентного уравнения 2-го порядка Общее решение рекуррентного уравнения 2-го порядка |
 Схема вывода формулы общего члена возвратной последовательности второго порядка Схема вывода формулы общего члена возвратной последовательности второго порядка |
 Примеры с решениями Примеры с решениями |
Определение возвратной последовательности
в каждой из которых символами b1 и q обозначены заданные числа – первый член и знаменатель прогрессии.
Определение . Пусть k – натуральное число. Возвратной (рекуррентной) последовательностью порядка k называют последовательность, для задания которой требуется задать первые её k членов, т.е. числа
а остальные члены последовательности определяются с помощью рекуррентной формулы (рекуррентного уравнения)
– заданные числа ( коэффициенты рекуррентной формулы ).
Замечание 1 . Числа
называют начальными условиями .
Замечание 2 . Для упрощения вычислений везде в дальнейшем будем рассматривать только случай возвратных последовательностей 2-го порядка, все члены которых являются вещественными числами.
Для задания таких последовательностей требуется задать их первые два члена, то есть вещественные числа x1 и x2 , а остальные члены последовательности
| xn = q1 xn – 1 + q2 xn – 2 , n > 2 , | (1) |
Характеристическое уравнение
Для того, чтобы получить характеристическое уравнение возвратной последовательности (1), будем искать такие числа λ , при которых последовательность вида
| xn = λ n | (2) |
удовлетворяет рекуррентной формуле (1).
| xn – 1 = λ n – 1 , xn – 2 = λ n – 2 , | (3) |
то при подстановке формул (2) и (3) в формулу (1) возникает уравнение
которое удобно переписать в виде
| λ n – q1 λ n – 1 – – q2 λ n – 2 = 0 . | (4) |
Если теперь уравнение (4) разделить на λ n–2 , то мы получим квадратное уравнение относительно λ вида:
которое и называют характеристическим уравнением .
Общее решение рекуррентного уравнения второго порядка
В случае, когда характеристическое уравнение имеет два различных вещественных корня λ1 и λ2 , каждая из последовательностей
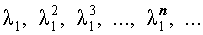
и
удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c1 и c2 последовательность с общим членом
также удовлетворяет рекуррентной формуле (1).
Числа c1 и c2 называют произвольными постоянными .
В случае, когда характеристическое уравнение имеет два совпавших вещественных корня λ1 = λ2 , непосредственная проверка показывает, что каждая из последовательностей
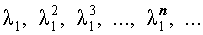
и
удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c1 и c2 последовательность с общим членом
также удовлетворяет рекуррентной формуле (1).
В случае, когда характеристическое уравнение имеет два комплексно-сопряженных корня λ1, 2 = α ± i β, каждая из последовательностей
удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c1 и c2 последовательность с общим членом
также удовлетворяет рекуррентной формуле (1).
Ряд примеров, в которых выводятся формулы общего члена возвратных последовательностей, разобран в разделе «Возвратные последовательности: вывод формулы общего члена» нашего справочника.
Please wait.
We are checking your browser. gufo.me
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6de50ea6f8641697 • Your IP : 85.95.188.35 • Performance & security by Cloudflare
ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ
Найдено 12 изображений:
ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ в математике, 1) Х. у. матрицы — алгебр. ур-ние вида
из диагональных элементов. Этот определитель представляет собой многочлен относительно X — характеристический многочлен. В раскрытом виде X. у. записывается так:
венными значениями матрицы А. У действительной симметричной матрицы, а также у эрмитовой матрицы все Хи действительны, у действительной кососимметричной матрицы все X* чисто мнимые числа; в случае действительной ортогональной матрицы, а также унитар-
X. у. встречаются в самых разнообразных областях математики, механики, физики, техники. В астрономии при определении вековых возмущений планет также приходят к X. у.; отсюда и второе название для X. у. — вековое уравнение.
2)Х. у. линейного дифференциального уравнения с постоянными коэффициентами
-алгебр, ур-ние, к-рое получается из да ного дифференциального ур-ния пос. замены функции y и её производных с ответствующими степенями величины т. е. ур-ние
составленной из коэфф. ур-ний данной системы.
Характеристи́ческое уравне́ние. Во многих случаях физические процессы, происходящие в системах, описываются системой обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами, которая в достаточно общем случае может быть сведена к дифференциальному уравнению вида
[при F(t) ≡ 0 это уравнение называется однородным]. Здесь a1, b1 постоянные коэффициенты, выражающиеся, например, через аэродинамические коэффициенты; Z(t) неизвестная функция времени t; F(t) заданное, зависящее от времени внешнее возмущение.Если ввести обозначение d i /dt i = p i так, что d i Z(t)/dt i = p i Z(t), то это уравнение можно переписать в виде L(p)Z(t) = S(p)F(t), где L(p) и S(p) некоторые многочлены степеней n и m соответственно. Полученный таким образом многочлен L(p) = p n + a1p n ‑1 + + an-1p + an называется характеристическим многочленом (полиномом), а уравнение L(p) = 0 характеристическим уравнением (существуют и другие способы получения Х. у. см., например, ст. Передаточная функция). Корни Х. у. определяют вид решения линейного однородного дифференциального уравнения и тем самым тип собственного движения системы (периодические, затухающее и т. п.). Х. у. линейной системы не зависит от того, относительно какой из её переменных (например, скорость полёта или угол атаки при исследовании продольного движения) составляется дифференциальное уравнение и какие возмущающие и задающие воздействия в эту систему вводятся.
Необходимым и достаточным условием устойчивости решения системы обыкновенных линейных дифференциальных уравнений является отрицательность всех действительных частей корней Х. у. При этом оказывается, что положительность всех коэффициентов характеристического полинома является необходимым и достаточным условием устойчивости для систем первого и второго порядков и лишь необходимым условием устойчивости (обеспечивается отрицательность только вещественных корней) для систем третьего и более высоких порядков. Существуют различные способы исследования на основе Х. у. устойчивости систем, например метод построения областей устойчивости, алгебраические и частотные критерии. Х. у. широко используется при исследовании динамики полёта, устойчивости летательного аппарата и его управляемости.
Попов Е. П., Динамика систем автоматического регулирования, М., 1954;
Понтрягин Л. С., Обыкновенные дифференциальные уравнения, 4 изд., М., 1974.
http://gufo.me/dict/bse/%D0%A5%D0%B0%D1%80%D0%B0%D0%BA%D1%82%D0%B5%D1%80%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5
http://slovaronline.com/browse/85a8c78d-8dbb-3299-8b6c-fa2aaed4b7e3/%D1%85%D0%B0%D1%80%D0%B0%D0%BA%D1%82%D0%B5%D1%80%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5-%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5