Что такое кинематическое уравнение равноускоренного движения

Равноускоренное движение: формулы, примеры

Равноускоренное движение

Равноускоренное движение — это движение, при котором вектор ускорения не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение — частный случай равноускоренного движения с ускорением, равным нулю.

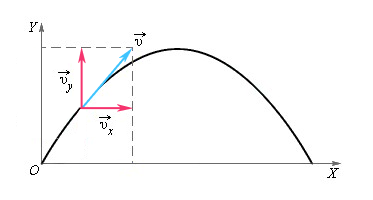
Рассмотрим случай свободного падения (тело брошено под уголом к горизонту) более подробно. Такое движение можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.

В любой точке траектории на тело действует ускорение свободного падения g → , которое не меняется по величине и всегда направлено в одну сторону.

Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y — равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.

Формулы для равноускоренного движения

Формула для скорости при равноускоренном движении:

Здесь v 0 — начальная скорость тела, a = c o n s t — ускорение.

Покажем на графике, что при равноускоренном движении зависимость v ( t ) имеет вид прямой линии.

​​​​​​​

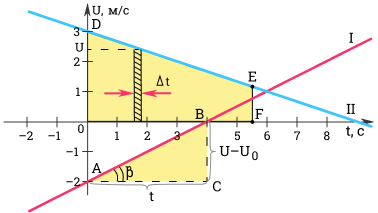
Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.

a = v — v 0 t = B C A C

Чем больше угол β , тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.

Для первого графика: v 0 = — 2 м с ; a = 0 , 5 м с 2 .

Для второго графика: v 0 = 3 м с ; a = — 1 3 м с 2 .

По данному графику можно также вычислить перемещение тела за время t . Как это сделать?

Выделим на графике малый отрезок времени ∆ t . Будем считать, что он настолько мал, что движение за время ∆ t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆ t . Тогда, перемещение ∆ s за время ∆ t будет равно ∆ s = v ∆ t .

Разобьем все время t на бесконечно малые промежутки ∆ t . Перемещение s за время t равно площади трапеции O D E F .

s = O D + E F 2 O F = v 0 + v 2 t = 2 v 0 + ( v — v 0 ) 2 t .

Мы знаем, что v — v 0 = a t , поэтому окончательная формула для перемещения тела примет вид:

s = v 0 t + a t 2 2

Для того, чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение. Изменение координаты в зависимости от времени выражает закон равноускоренного движения.

Закон равноускоренного движения

y = y 0 + v 0 t + a t 2 2 .

Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения — нахождение координаты при заданных значениях начальной и конечной скоростей и ускорения.

Исключая из записанных выше уравнений t и решая их, получаем:

s = v 2 — v 0 2 2 a .

По известным начальной скорости, ускорению и перемещению можно найти конечную скорость тела:

v = v 0 2 + 2 a s .

При v 0 = 0 s = v 2 2 a и v = 2 a s

Величины v , v 0 , a , y 0 , s , входящие в выражения, являются алгебраическими величинами. В зависимости от характера движения и направления координатных осей в условиях конкретной задачи они могут принимать как положительные, так и отрицательные значения.

Формула равноускоренного движения

Определение и формула равноускоренного движения

Движение, при котором за любые равные промежутки времени скорость меняется на одну величину, называют равнопеременным. Если скорость при этом увеличивается, то такое движение носит название равноускоренного движения.

Равноускоренное движение можно определить еще как движение, при котором модуль касательного ускорения ($a_<\tau>=$ const $>0$).

Основные кинематические величины при равноускоренном движении

где v₂ – конечная скорость, v₁— начальнаяскорость движения, t–время движения.

Скорость в любой момент равноускоренного прямолинейного движения можно найти как:

где $\bar_0$ – начальная скорость движения.

Уравнение для координаты материальной при равноускоренном движении записывают как:

где v_0x – проекция начальной скорости на ось X, a_x – проекция ускорения на ось X.

Перемещение при равноускоренном движении является функцией вида:

где $\bar_0$ – перемещение в начальный момент времени. Или $\bar$ еще можно представить как:

Примеры решения задач

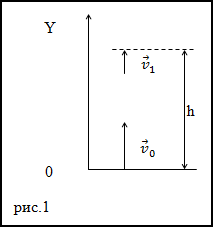
Задание. Тело было брошено вертикально вверх. Оно возвратилось на землю через промежуток времени, равный t. Какой была начальная скорость тела, и на какую высоту оно поднялось?

Решение. Тело в поле тяжести Земли движется с постоянным ускорением равным ускорению свободного падения, на рис.1 оно направлено вниз.

В качестве основы для решения задачи используем формулу для перемещения при равноускоренном движении:

Все движение происходит только по оси Y, поэтому проекция выражения (1.1) примет вид:

Формула для скорости при равноускоренном движении записывается как:

В проекции на ось она преобразуется к виду:

Точке максимального подъема мы имеем y(t₁)=h и v(t₁)=0 (t₁ — время поъема), тогда выражения (1.2) и (1.4) перепишем как:

где $t_<1>=\frac<2>$ . Следовательно,

Подставляя выражение (1.6) вместо начальной скорости в формулу h, имеем:

Методическая разработка на тему Кинематика

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Лекция Кинематика.doc

Лекция №1: « Кинематика материальной точки»

1.Основные понятия кинематики

2.Кинематические характеристики поступательного движения материальной точки

2.1 Путь, перемещение

2.2 Скорость средняя и мгновенная

2.3 Ускорение и его составляющие

2.4 Кинематические уравнения основных видов движения

2.4.1 Кинематические уравнения прямолинейного равномерного движения

2.4.2 Кинематические уравнения равноускоренного движения

3.Кинематические характеристики вращательного движения материальной точки

3.1 Угловой путь

3.2 Угловая скорость (средняя и мгновенная)

3.3 Угловое ускорение (среднее и мгновенное)

3.4 Период, частота

4. Кинематические уравнения основных видов движения по окружности

4.1 Кинематическое уравнение равномерного движения по окружности

4.2 Кинематическое уравнение равноускоренного движения по окружности

5.Связь между линейными и угловыми кинематическими характеристиками

1.Основные понятия кинематики

Часть физики, изучающая механическое движение тел, называется механикой. Основные законы механики установлены Галилео Галилеем ( G . Galilei 1564-1642) и окончательно сформулированы Исааком Ньютоном ( I . Newton 1643-1727). Механику Галилея-Ньютона называют классической механикой. В ней изучаются законы движения макроскопических тел (это все окружающие нас тела) со скоростями, малыми по сравнению со скоростью света. Более общей теорией, в которой описываются и микроскопические тела (например, элементарные частицы) является, квантовая механика. Движение макроскопических тел с любыми скоростями, в том числе и со скоростями, сравнимыми со скоростью света, рассматривает релятивистская механика. Механика делится на 3 раздела: кинематику, динамику и статику.

Раздел физики, в котором механическое движение изучается без рассмотрения причин, определяющих характер движения, называется кинематикой. Основная задача кинематики – определение положения тела в пространстве и характеристик его движения в любой момент времени.

Механическим движением называют изменение с течением времени положения тела в пространстве.

Основными видами механического движения являются поступательное и вращательное движения.

Поступательным движением называется движение, при котором любая прямая, связанная с движущимся телом, остаётся параллельной самой себе. При поступательном движении все точки тела движутся одинаково, поэтому можно рассматривать движение тела независимо от его размеров и формы, как движение одной точки тела.

Вращательным движением называют движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.

Простейшей моделью тела является материальная точка. Материальной точкой называется обладающее массой тело, размерами которого можно пренебречь в данной задаче. Если размерами тела пренебречь нельзя, то его можно представить как совокупность материальных точек, рассматриваемых как единое целое, — то есть как систему материальных точек. В процессе движения расстояние между точками, составляющими тело, может меняться – в этом случае говорят о деформации тела. Если при рассмотрении движения деформация тела незначительна (ею можно пренебречь), тогда в качестве модели тела можно использовать модель абсолютно твердого тела. Абсолютно твердым телом называется тело, расстояние между двумя любыми точками которого не изменяется.

Для описания механического движения (изменение положения тела) вводят систему отчета. Системой отсчета называют тело отсчета, относительно которого определяется положение всех других тел, и связанные с этим телом часы.

Для определения положения материальной точки введем радиус-вектор материальной точки r – вектор, проведенный из начала отсчета (начала системы координат) в рассматриваемую материальную точку. Проекции радиус-вектора на оси OX , OY , OZ равны декартовым координатам точки = x , r = y , r = z .

При движении материальной точки её координаты с течением времени изменяются. В общем случае её движение определяется скалярными уравнениями:

,

Эти уравнения называются кинематическими уравнениями движения материальной точки.

2.Кинематические характеристики поступательного

движения материальной точки.

При движении точка (конец радиус-вектора) описывает некоторую линию – траекторию движения.

Траектория движения материальной точки – линия, представляющая собой совокупность точек, через которые прошла материальная точка в процессе её движения. В зависимости от формы линии траектория может быть прямолинейной или криволинейной.

Для описания движения введем физические величины, которыми будем характеризовать движение, они называются кинематическими характеристиками.

2.1 Путь, перемещение.

Путь S , пройденный материальной точкой – скалярная величина, равная длине участка траектории, который прошла точка за данный промежуток времени.

Перемещение за время — вектор, соединяющий некоторое положение точки с её положением спустя время :

При неравномерном движении – модуль мгновенной скорости с течением времени изменяется. Длина пути в данном случае вычисляется по формуле:

, .

2.2 Скорость средняя и мгновенная

Для характеристики движения материальной точки вводится векторная величина – скорость, которая определяет быстроту движения и направление в данный момент времени.

Средняя скорость – это векторная величина, численно равная отношению приращения радиус вектора к промежутку времени за который это приращение произошло :

, .

Направление вектора средней скорости совпадает с направлением радиус-вектора.

Мгновенная скорость – это векторная величина, численно равная пределу отношения перемещения к промежутку времени при стремлении данного промежутка к нулю, или является первой производной перемещения по времени:

, .

2.3 Ускорение и его составляющие

Скорость материальной точки может изменяться со временем как по величине, так и по его направлению. Быстрота изменения скорости характеризуется ускорением.

Среднее ускорение – это векторная физическая величина, численно равная отношению изменения скорости к промежутку времени, за который это изменение произошло:

, .

Мгновенное ускорение – это векторная величина, численно равная пределу отношения изменения скорости к промежутку времени при стремлении данного промежутка к нулю, или является первой производной скорости по времени, или второй производной перемещения по времени:

,

При равномерном движении по окружности ускорение разлагается на две составляющие: нормальную и тангенциальную.

Тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю и направлена по касательной к траектории:

.

Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению и направлена к центру кривизны траектории: , r — радиус кривизны траектории.

Полное ускорение – геометрическая сумма тангенциальной и нормальной составляющих:

, или в скалярном виде:.

2.4 Кинематические уравнения основных видов движения.

Рассмотрим частные случаи движения материальной точки, определяемые свойствами кинематических характеристик, и получим для этих случаев кинематические уравнения – зависимости кинематических характеристик от времени.

2.4.1.Равномерное прямолинейное движение , .

По определению или . Интегрируя левую часть от до и правую часть от до , , получаем , или .

Полученная зависимость радиус-вектора от времени вместе с выражениями, , представляют собой кинематические уравнения прямолинейного равномерного движения в векторном виде. Если ось OX направить вдоль направления скорости (вдоль траектории, которая прямолинейна), то уравнение для радиус-вектора в проекции на эту ось будет иметь вид , а путь, пройденный к моменту времени , будет определяться .

2.4.2Равноускоренное движение

По определению или . Интегрируя , получаем: или . Далее учтем, что , следовательно, . Интегрируя левую и правую части, получим .

Таким образом, в векторной форме кинематические уравнения равноускоренного движения имеют вид:

, , .

Одним из видов равноускоренного движения является свободное падение. Кинематические уравнения свободного падения имеют вид:

, , .

Примером равноускоренного движения является баллистическое движение без учета сопротивления воздуха – свободное движение тел в поле силы тяжести, в проекциях на оси X и Y кинематические уравнения примут вид:

Для тела, брошенного с начальной скоростью под углом к горизонту из начала координат, кинематические уравнения запишутся в виде:

и .

Траектория движения будет параболой, описываемой уравнением:

.

Из кинематических уравнений могут быть получены параметры полета тела: время полета , высота подъема , дальность полета :

, , .

3. Кинематические характеристики вращательного

движения материальной точки

3.1 Угловой путь

Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдельные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R . Её положение через промежуток времени зададим углом .

Угловой путь – это элементарный угол поворота:

, .

Радиан – это угол, который вырезает на окружности дугу, равную радиусу.

Направление углового пути определяется правилом правого винта: если головку винта вращать в направлении движения точки по окружности, то поступательное движение острия винта укажет направление .

Векторы, направления которых связываются с направлением вращения, называются псевдовекторами или аксиальными векторами. Эти векторы не имеют определенных точек приложения, они могут откладываться от любой точки оси вращения.

3.2 Угловая скорость (средняя и мгновенная)

Средняя угловая скорость – это физическая величина, численно равная отношению углового пути к промежутку времени:

, .

Мгновенная угловая скорость – это физическая величина, численно равная изменения пределу отношения углового пути к промежутку времени при стремлении данного промежутка к нулю, или является первой производной углового пути по времени:

, .

3.3 Угловое ускорение (среднее и мгновенное)

Среднее угловое ускорение – это физическая величина, численно равная отношению изменения угловой скорости к промежутку времени, за который это изменение произошло:

, .

Мгновенное угловое ускорение – это физическая величина, численно равная пределу отношения изменения угловой скорости к промежутку времени при стремлении данного промежутка к нулю, или является первой производной угловой скорости по времени, или второй производной углового пути по времени:

, .

При ускоренном движении угловое ускорение совпадает по направлению с угловой скоростью. При замедленном вращении угловое ускорение направлено в противоположную относительно угловой скорости сторону.

3.4 Период, частота

Период – время одного полного оборота материальной точки.

,

Частота – число оборотов материальной точки в единицу времени.

,

4. Кинематические уравнения основных видов движения по окружности

Кинематические уравнения равномерного движения по окружности

При равномерном движении материальной точки по окружности кинематические уравнения в угловых переменных будут иметь вид:

, , .

Кинематические уравнения равноускоренного движения по окружности

При движении материальной точки по окружности с постоянным угловым ускорением кинематические уравнения будут иметь вид, аналогичный прямолинейному равноускоренному движению (процедура получения уравнений одинаковая):

, , .

5. Связь между линейными и угловыми величинами

Очевидно, что угловые переменные, введенные для вращения, и линейные переменные должны быть связаны друг с другом, так как с помощью тех и других можно описать одно и то же движение. Найдем эту связь.

По определению единицы измерения угла – радиана, дуга S окружности связана с радиусом окружности R соотношением или для приращений .

По определению величина скорости (модуль вектора скорости ) равна .

При длина хорды стремится к длине дуги , то есть , или . Тогда .

Окончательно получаем , то есть связь между скоростями имеет такой же вид, как связь между S и : .

В векторном виде, с учетом направлений векторов, можем записать: , где — радиус-вектор относительно центра вращения, его величина равна радиусу окружности, .

Теперь найдем связь между ускорениями. По определению , а поскольку

, то .

Первое слагаемое направлено по скорости, если , и против, если , то есть всегда параллельно скорости. Естественно, эту часть ускорения называют тангенциальной составляющей ускорения (тангенциальным ускорением):

.

Второе слагаемое направлено по радиусу к центру окружности, то есть перпендикулярно скорости. Эту часть ускорения называют нормальной составляющей ускорения (нормальным ускорением):