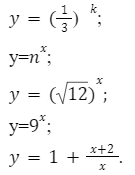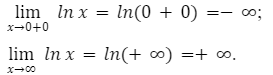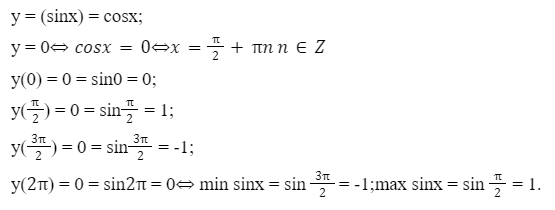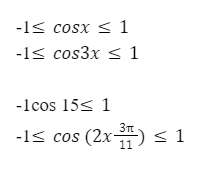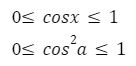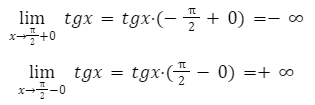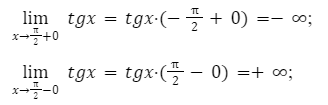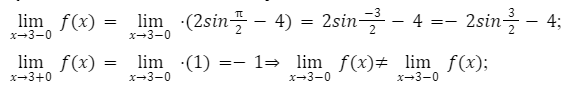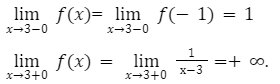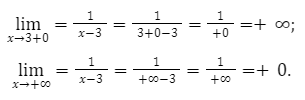Что такое область значения уравнения

Область значений функции (множество значений функции). Необходимые понятия и примеры нахождения

Зачастую в рамках решения задач нам приходится искать множество значений функции на области определения или отрезке. Например, это нужно делать при решении разных типов неравенств, оценках выражений и др.

В рамках этого материала мы расскажем, что из себя представляет область значений функции, приведем основные методы, которыми ее можно вычислить, и разберем задачи различной степени сложности. Для наглядности отдельные положения проиллюстрированы графиками. Прочитав эту статью, вы получите исчерпывающее представление об области значений функции.

Начнем с базовых определений.

Множество значений функции y = f ( x ) на некотором интервале x представляет собой множество всех значений, которые данная функция принимает при переборе всех значений x ∈ X .

Область значений функции y = f ( x ) – это множество всех ее значений, которые она может принять при переборе значений x из области x ∈ ( f ) .

Область значений некоторой функции принято обозначать E ( f ) .

Обратите внимание, что понятие множества значений функции не всегда тождественно области ее значений. Эти понятия будут равнозначны только в том случае, если интервал значений x при нахождении множества значений совпадет с областью определения функции.

Важно также различать область значений и область допустимых значений переменной x для выражения в правой части y = f ( x ) . Область допустимых значений x для выражения f ( x ) и будет областью определения данной функции.

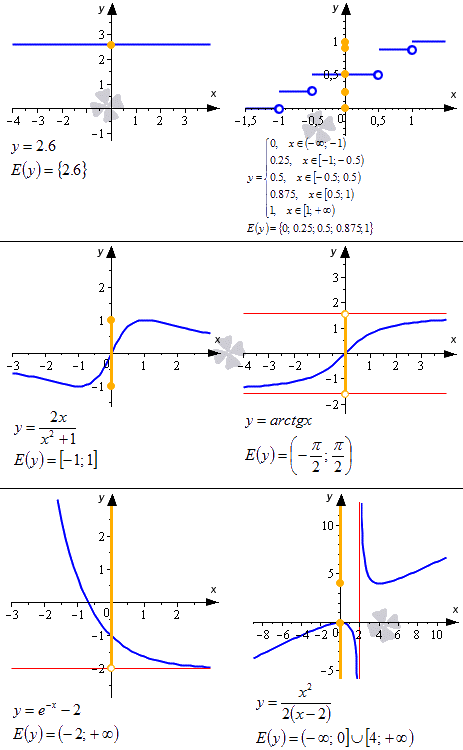
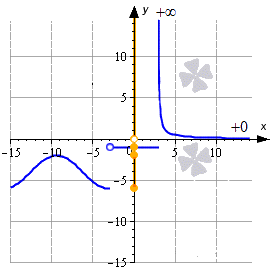
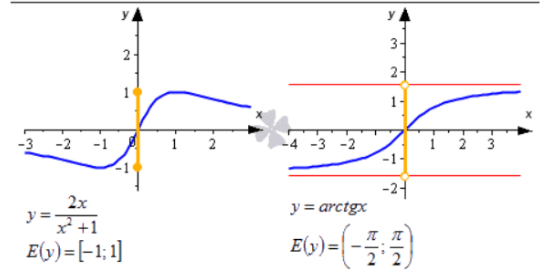
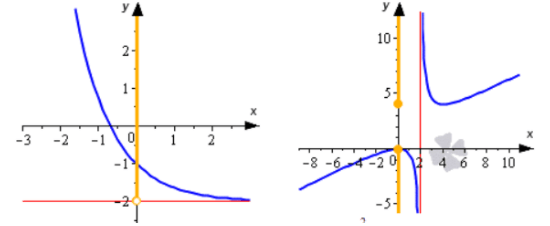
Ниже приводится иллюстрация, на которой показаны некоторые примеры. Синие линии – это графики функций, красные – асимптоты, рыжие точки и линии на оси ординат – это области значений функции.

Очевидно, что область значений функции можно получить при проецировании графика функции на ось O y . При этом она может представлять собой как одно число, так и множество чисел, отрезок, интервал, открытый луч, объединение числовых промежутков и др.

Рассмотрим основные способы нахождения области значений функции.

Начнем с определения множества значений непрерывной функции y = f ( x ) на некотором отрезке, обозначенном [ a ; b ] . Мы знаем, что функция, непрерывная на некотором отрезке, достигает на нем своего минимума и максимума, то есть наибольшего m a x x ∈ a ; b f ( x ) и наименьшего значения m i n x ∈ a ; b f ( x ) . Значит, у нас получится отрезок m i n x ∈ a ; b f ( x ) ; m a x x ∈ a ; b f ( x ) , в котором и будут находиться множества значений исходной функции. Тогда все, что нам нужно сделать, – это найти на этом отрезке указанные точки минимума и максимума.

Возьмем задачу, в которой нужно определить область значений арксинуса.

Условие: найдите область значений y = a r c sin x .

Решение

В общем случае область определения арксинуса располагается на отрезке [ — 1 ; 1 ] . Нам надо определить наибольшее и наименьшее значение указанной функции на нем.

y ‘ = a r c sin x ‘ = 1 1 — x 2

Мы знаем, что производная функции будет положительной для всех значений x , расположенных в интервале [ — 1 ; 1 ] , то есть на протяжении всей области определения функция арксинуса будет возрастать. Значит, самое маленькое значение она примет при x , равном — 1 , а самое большое – при x , равном 1 .

m i n x ∈ — 1 ; 1 a r c sin x = a r c sin — 1 = — π 2 m a x x ∈ — 1 ; 1 a r c sin x = a r c sin 1 = π 2

Таким образом, область значений функции арксинус будет равна E ( a r c sin x ) = — π 2 ; π 2 .

Ответ: E ( a r c sin x ) = — π 2 ; π 2

Условие: вычислите область значений y = x 4 — 5 x 3 + 6 x 2 на заданном отрезке [ 1 ; 4 ] .

Решение

Все, что нам нужно сделать, – это вычислить наибольшее и наименьшее значение функции в заданном интервале.

Для определения точек экстремума надо произвести следующие вычисления:

y ‘ = x 4 — 5 x 3 + 6 x 2 ‘ = 4 x 3 + 15 x 2 + 12 x = x 4 x 2 — 15 x + 12 y ‘ = 0 ⇔ x ( 4 x 2 — 15 x + 12 ) = 0 x 1 = 0 ∉ 1 ; 4 и л и 4 x 2 — 15 x + 12 = 0 D = — 15 2 — 4 · 4 · 12 = 33 x 2 = 15 — 33 8 ≈ 1 . 16 ∈ 1 ; 4 ; x 3 = 15 + 33 8 ≈ 2 . 59 ∈ 1 ; 4

Теперь найдем значения заданной функции в концах отрезка и точках x 2 = 15 — 33 8 ; x 3 = 15 + 33 8 :

y ( 1 ) = 1 4 — 5 · 1 3 + 6 · 1 2 = 2 y 15 — 33 8 = 15 — 33 8 4 — 5 · 15 — 33 8 3 + 6 · 15 — 33 8 2 = = 117 + 165 33 512 ≈ 2 . 08 y 15 + 33 8 = 15 + 33 8 4 — 5 · 15 + 33 8 3 + 6 · 15 + 33 8 2 = = 117 — 165 33 512 ≈ — 1 . 62 y ( 4 ) = 4 4 — 5 · 4 3 + 6 · 4 2 = 32

Значит, множество значений функции будет определяться отрезком 117 — 165 33 512 ; 32 .

Ответ: 117 — 165 33 512 ; 32 .

Перейдем к нахождению множества значений непрерывной функции y = f ( x ) в промежутках ( a ; b ) , причем a ; + ∞ , — ∞ ; b , — ∞ ; + ∞ .

Начнем с определения наибольшей и наименьшей точки, а также промежутков возрастания и убывания на заданном интервале. После этого нам нужно будет вычислить односторонние пределы в концах интервала и/или пределы на бесконечности. Иными словами, нам надо определить поведении функции в заданных условиях. Для этого у нас есть все необходимые данные.

Условие: вычислите область значений функции y = 1 x 2 — 4 на интервале ( — 2 ; 2 ) .

Решение

Определяем наибольшее и наименьшее значение функции на заданном отрезке

y ‘ = 1 x 2 — 4 ‘ = — 2 x ( x 2 — 4 ) 2 y ‘ = 0 ⇔ — 2 x ( x 2 — 4 ) 2 = 0 ⇔ x = 0 ∈ ( — 2 ; 2 )

У нас получилось максимальное значение, равное 0 , поскольку именно в этой точке происходит перемена знака функции и график переходит к убыванию. См. на иллюстрацию:

То есть y ( 0 ) = 1 0 2 — 4 = — 1 4 будет максимальным значений функции.

Теперь определим поведение функции при таком x, который стремится к — 2 с правой стороны и к + 2 с левой стороны. Иными словами, найдем односторонние пределы:

lim x → — 2 + 0 1 x 2 — 4 = lim x → — 2 + 0 1 ( x — 2 ) ( x + 2 ) = = 1 — 2 + 0 — 2 — 2 + 0 + 2 = — 1 4 · 1 + 0 = — ∞ lim x → 2 + 0 1 x 2 — 4 = lim x → 2 + 0 1 ( x — 2 ) ( x + 2 ) = = 1 2 — 0 — 2 2 — 0 + 2 = 1 4 · 1 — 0 = — ∞

У нас получилось, что значения функции будут возрастать от минус бесконечности до — 1 4 тогда, когда аргумент изменяется в пределах от — 2 до 0 . А когда аргумент меняется от 0 до 2 , значения функции убывают к минус бесконечности. Следовательно, множеством значений заданной функции на нужном нам интервале будет ( — ∞ ; — 1 4 ] .

Ответ: ( — ∞ ; — 1 4 ] .

Условие: укажите множество значений y = t g x на заданном интервале — π 2 ; π 2 .

Решение

Нам известно, что в общем случае производная тангенса в — π 2 ; π 2 будет положительной, то есть функция будет возрастать. Теперь определим, как ведет себя функция в заданных границах:

lim x → π 2 + 0 t g x = t g — π 2 + 0 = — ∞ lim x → π 2 — 0 t g x = t g π 2 — 0 = + ∞

Мы получили рост значений функции от минус бесконечности к плюс бесконечности при изменении аргумента от — π 2 до π 2 ,и можно сказать, что множеством решений данной функции будет множество всех действительных чисел.

Ответ: — ∞ ; + ∞ .

Условие: определите, какова область значений функции натурального логарифма y = ln x .

Решение

Нам известно, что данная функция является определенной при положительных значениях аргумента D ( y ) = 0 ; + ∞ . Производная на заданном интервале будет положительной: y ‘ = ln x ‘ = 1 x . Значит, на нем происходит возрастание функции. Далее нам нужно определить односторонний предел для того случая, когда аргумент стремится к 0 (в правой части), и когда x стремится к бесконечности:

lim x → 0 + 0 ln x = ln ( 0 + 0 ) = — ∞ lim x → ∞ ln x = ln + ∞ = + ∞

Мы получили, что значения функции будут возрастать от минус бесконечности до плюс бесконечности при изменении значений x от нуля до плюс бесконечности. Значит, множество всех действительных чисел – это и есть область значений функции натурального логарифма.

Ответ: множество всех действительных чисел – область значений функции натурального логарифма.

Условие: определите, какова область значений функции y = 9 x 2 + 1 .

Решение

Данная функция является определенной при условии, что x – действительное число. Вычислим наибольшие и наименьшие значения функции, а также промежутки ее возрастания и убывания:

y ‘ = 9 x 2 + 1 ‘ = — 18 x ( x 2 + 1 ) 2 y ‘ = 0 ⇔ x = 0 y ‘ ≤ 0 ⇔ x ≥ 0 y ‘ ≥ 0 ⇔ x ≤ 0

В итоге мы определили, что данная функция будет убывать, если x ≥ 0 ; возрастать, если x ≤ 0 ; она имеет точку максимума y ( 0 ) = 9 0 2 + 1 = 9 при переменной, равной 0 .

Посмотрим, как же ведет себя функция на бесконечности:

lim x → — ∞ 9 x 2 + 1 = 9 — ∞ 2 + 1 = 9 · 1 + ∞ = + 0 lim x → + ∞ 9 x 2 + 1 = 9 + ∞ 2 + 1 = 9 · 1 + ∞ = + 0

Из записи видно, что значения функции в этом случае будут асимптотически приближаться к 0.

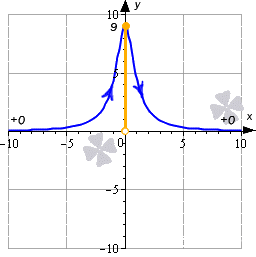
Подведем итоги: когда аргумент изменяется от минус бесконечности до нуля, то значения функции возрастают от 0 до 9 . Когда значения аргумента меняются от 0 до плюс бесконечности, соответствующие значения функции будут убывать от 9 до 0 . Мы отобразили это на рисунке:

На нем видно, что областью значений функции будет интервал E ( y ) = ( 0 ; 9 ]

Ответ: E ( y ) = ( 0 ; 9 ]

Если нам надо определить множество значений функции y = f ( x ) на промежутках [ a ; b ) , ( a ; b ] , [ a ; + ∞ ) , ( — ∞ ; b ] , то нам понадобится провести точно такие же исследования. Эти случаи мы пока не будем разбирать: далее они нам еще встретятся в задачах.

А как быть в случае, если область определения некоторой функции представляет из себя объединение нескольких промежутков? Тогда нам надо вычислить множества значений на каждом из этих промежутков и объединить их.

Условие: определите, какова будет область значений y = x x — 2 .

Решение

Поскольку знаменатель функции не должен быть обращен в 0 , то D ( y ) = — ∞ ; 2 ∪ 2 ; + ∞ .

Начнем с определения множества значений функции на первом отрезке — ∞ ; 2 , который представляет из себя открытый луч. Мы знаем, что функция на нем будет убывать, то есть производная данной функции будет отрицательной.

lim x → 2 — 0 x x — 2 = 2 — 0 2 — 0 — 2 = 2 — 0 = — ∞ lim x → — ∞ x x — 2 = lim x → — ∞ x — 2 + 2 x — 2 = lim x → — ∞ 1 + 2 x — 2 = 1 + 2 — ∞ — 2 = 1 — 0

Тогда в тех случаях, когда аргумент изменяется по направлению к минус бесконечности, значения функции будут асимптотически приближаться к 1 . Если же значения x меняются от минус бесконечности до 2 , то значения будут убывать от 1 до минус бесконечности, т.е. функция на этом отрезке примет значения из интервала — ∞ ; 1 . Единицу мы исключаем из наших рассуждений, поскольку значения функции ее не достигают, а лишь асимптотически приближаются к ней.

Для открытого луча 2 ; + ∞ производим точно такие же действия. Функция на нем также является убывающей:

lim x → 2 + 0 x x — 2 = 2 + 0 2 + 0 — 2 = 2 + 0 = + ∞ lim x → + ∞ x x — 2 = lim x → + ∞ x — 2 + 2 x — 2 = lim x → + ∞ 1 + 2 x — 2 = 1 + 2 + ∞ — 2 = 1 + 0

Значения функции на данном отрезке определяются множеством 1 ; + ∞ . Значит, нужная нам область значений функции, заданной в условии, будет объединением множеств — ∞ ; 1 и 1 ; + ∞ .

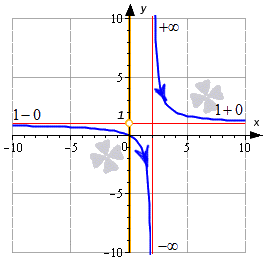
Ответ: E ( y ) = — ∞ ; 1 ∪ 1 ; + ∞ .

Это можно увидеть на графике:

Особый случай – периодические функции. Их область значения совпадает с множеством значений на том промежутке, который отвечает периоду этой функции.

Условие: определите область значений синуса y = sin x .

Решение

Синус относится к периодической функции, а его период составляет 2 пи. Берем отрезок 0 ; 2 π и смотрим, каким будет множество значений на нем.

y ‘ = ( sin x ) ‘ = cos x y ‘ = 0 ⇔ cos x = 0 ⇔ x = π 2 + πk , k ∈ Z

В рамках 0 ; 2 π у функции будут точки экстремума π 2 и x = 3 π 2 . Подсчитаем, чему будут равны значения функции в них, а также на границах отрезка, после чего выберем самое большое и самое маленькое значение.

y ( 0 ) = sin 0 = 0 y π 2 = sin π 2 = 1 y 3 π 2 = sin 3 π 2 = — 1 y ( 2 π ) = sin ( 2 π ) = 0 ⇔ min x ∈ 0 ; 2 π sin x = sin 3 π 2 = — 1 , max x ∈ 0 ; 2 π sin x = sin π 2 = 1

Ответ: E ( sin x ) = — 1 ; 1 .

Если вам нужно знать области значений таких функций, как степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая, то советуем вам перечитать статью об основных элементарных функциях. Теория, которую мы приводим здесь, позволяет проверить указанные там значения. Их желательно выучить, поскольку они часто требуются при решении задач. Если вы знаете области значений основных функций, то легко сможете находить области функций, которые получены из элементарных с помощью геометрического преобразования.

Условие: определите область значения y = 3 a r c cos x 3 + 5 π 7 — 4 .

Решение

Нам известно, что отрезок от 0 до пи есть область значений арккосинуса. Иными словами, E ( a r c cos x ) = 0 ; π или 0 ≤ a r c cos x ≤ π . Мы можем получить функцию a r c cos x 3 + 5 π 7 из арккосинуса, сдвинув и растянув ее вдоль оси O x , но такие преобразования нам ничего не дадут. Значит, 0 ≤ a r c cos x 3 + 5 π 7 ≤ π .

Функция 3 a r c cos x 3 + 5 π 7 может быть получена из арккосинуса a r c cos x 3 + 5 π 7 с помощью растяжения вдоль оси ординат, т.е. 0 ≤ 3 a r c cos x 3 + 5 π 7 ≤ 3 π . Финалом преобразований является сдвиг вдоль оси O y на 4 значения. В итоге получаем двойное неравенство:

0 — 4 ≤ 3 a r c cos x 3 + 5 π 7 — 4 ≤ 3 π — 4 ⇔ — 4 ≤ 3 arccos x 3 + 5 π 7 — 4 ≤ 3 π — 4

Мы получили, что нужная нам область значений будет равна E ( y ) = — 4 ; 3 π — 4 .

Ответ: E ( y ) = — 4 ; 3 π — 4 .

Еще один пример запишем без пояснений, т.к. он полностью аналогичен предыдущему.

Условие: вычислите, какова будет область значений функции y = 2 2 x — 1 + 3 .

Решение

Перепишем функцию, заданную в условии, как y = 2 · ( 2 x — 1 ) — 1 2 + 3 . Для степенной функции y = x — 1 2 область значений будет определена на промежутке 0 ; + ∞ , т.е. x — 1 2 > 0 . В таком случае:

2 x — 1 — 1 2 > 0 ⇒ 2 · ( 2 x — 1 ) — 1 2 > 0 ⇒ 2 · ( 2 x — 1 ) — 1 2 + 3 > 3

Значит, E ( y ) = 3 ; + ∞ .

Ответ: E ( y ) = 3 ; + ∞ .

Теперь разберем, как найти область значений функции, которая не является непрерывной. Для этого нам надо разбить всю область на промежутки и найти множества значений на каждом из них, после чего объединить то, что получилось. Чтобы лучше понять это, советуем повторить основные виды точек разрыва функции.

Условие: дана функция y = 2 sin x 2 — 4 , x ≤ — 3 — 1 , — 3 x ≤ 3 1 x — 3 , x > 3 . Вычислите область ее значений.

Решение

Данная функция является определенной для всех значений x . Проведем ее анализ на непрерывность при значениях аргумента, равных — 3 и 3 :

lim x → — 3 — 0 f ( x ) = lim x → — 3 2 sin x 2 — 4 = 2 sin — 3 2 — 4 = — 2 sin 3 2 — 4 lim x → — 3 + 0 f ( x ) = lim x → — 3 ( 1 ) = — 1 ⇒ lim x → — 3 — 0 f ( x ) ≠ lim x → — 3 + 0 f ( x )

Имеем неустранимый разрыв первого рода при значении аргумента — 3 . При приближении к нему значения функции стремятся к — 2 sin 3 2 — 4 , а при стремлении x к — 3 с правой стороны значения будут стремиться к — 1 .

lim x → 3 — 0 f ( x ) = lim x → 3 — 0 ( — 1 ) = 1 lim x → 3 + 0 f ( x ) = lim x → 3 + 0 1 x — 3 = + ∞

Имеем неустранимый разрыв второго рода в точке 3 . Когда функция стремится к нему, ее значения приближаются к — 1 , при стремлении к той же точке справа – к минус бесконечности.

Значит, вся область определения данной функции является разбитой на 3 интервала ( — ∞ ; — 3 ] , ( — 3 ; 3 ] , ( 3 ; + ∞ ) .

На первом из них у нас получилась функция y = 2 sin x 2 — 4 . Поскольку — 1 ≤ sin x ≤ 1 , получаем:

— 1 ≤ sin x 2 1 ⇒ — 2 ≤ 2 sin x 2 ≤ 2 ⇒ — 6 ≤ 2 sin x 2 — 4 ≤ — 2

Значит, на данном промежутке ( — ∞ ; — 3 ] множество значении функции – [ — 6 ; 2 ] .

На полуинтервале ( — 3 ; 3 ] получилась постоянная функция y = — 1 . Следовательно, все множество ее значений в данном случае будет сводится к одному числу — 1 .

На втором промежутке 3 ; + ∞ у нас есть функция y = 1 x — 3 . Она является убывающей, потому что y ‘ = — 1 ( x — 3 ) 2 0 . Она будет убывать от плюс бесконечности до 0 , но самого 0 не достигнет, потому что:

lim x → 3 + 0 1 x — 3 = 1 3 + 0 — 3 = 1 + 0 = + ∞ lim x → + ∞ 1 x — 3 = 1 + ∞ — 3 = 1 + ∞ + 0

Значит, множество значений исходной функции при x > 3 представляет собой множество 0 ; + ∞ . Теперь объединим полученные результаты: E ( y ) = — 6 ; — 2 ∪ — 1 ∪ 0 ; + ∞ .

Ответ: E ( y ) = — 6 ; — 2 ∪ — 1 ∪ 0 ; + ∞ .

Решение показано на графике:

Условие: есть функция y = x 2 — 3 e x . Определите множество ее значений.

Решение

Она определена для всех значений аргумента, представляющих собой действительные числа. Определим, в каких промежутках данная функция будет возрастать, а в каких убывать:

y ‘ = x 2 — 3 e x ‘ = 2 x e x — e x ( x 2 — 3 ) e 2 x = — x 2 + 2 x + 3 e x = — ( x + 1 ) ( x — 3 ) e x

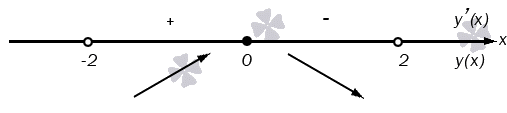
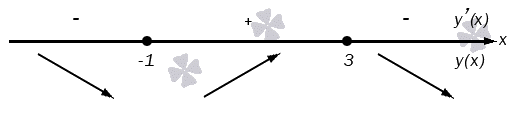
Мы знаем, что производная обратится в 0 , если x = — 1 и x = 3 . Поместим эти две точки на ось и выясним, какие знаки будет иметь производная на получившихся интервалах.

Функция будет убывать на ( — ∞ ; — 1 ] ∪ [ 3 ; + ∞ ) и возрастать на [ — 1 ; 3 ] . Точкой минимума будет — 1 , максимума – 3 .

Теперь найдем соответствующие значения функции:

y ( — 1 ) = — 1 2 — 3 e — 1 = — 2 e y ( 3 ) = 3 2 — 3 e 3 = 6 e — 3

Посмотрим на поведение функции на бесконечности:

lim x → — ∞ x 2 — 3 e x = — ∞ 2 — 3 e — ∞ = + ∞ + 0 = + ∞ lim x → + ∞ x 2 — 3 e x = + ∞ 2 — 3 e + ∞ = » open=» + ∞ + ∞ = = lim x → + ∞ x 2 — 3 ‘ e x ‘ = lim x → + ∞ 2 x e x = » open=» + ∞ + ∞ = = lim x → + ∞ 2 x ‘ ( e x ) ‘ = 2 lim x → + ∞ 1 e x = 2 · 1 + ∞ = + 0

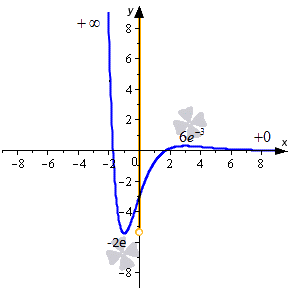
Для вычисления второго предела было использовано правило Лопиталя. Изобразим ход нашего решения на графике.

На нем видно, что значения функции будут убывать от плюс бесконечности до — 2 e тогда, когда аргумент меняется от минус бесконечности до — 1 . Если же он изменяется от 3 до плюс бесконечности, то значения будут убывать от 6 e — 3 до 0 , но при этом 0 достигнут не будет.

Таким образом, E ( y ) = [ — 2 e ; + ∞ ) .

Ответ: E ( y ) = [ — 2 e ; + ∞ )

Что такое область значений функции

В данной публикации мы рассмотрим, что такое область значений функции, как обозначается и задается. Также перечислим их для распространенных видов функций.

Определение области значений

Область значений – множество значений y , которые принимает функция при всех x , соответствующих ее области определения.

Примечание: каждому y соответствует только одно конкретное значение x .

Область значений обозначается как E(f) . Ее границы указываются так же, как и для области определений – в круглых или квадратных скобках.

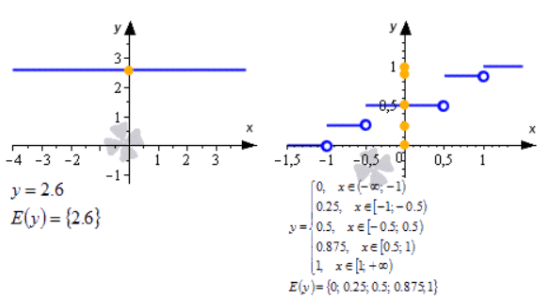
• E(f) = (0; ∞).
  Т.е. область значений функции – от нуля исключительно до плюс бесконечности, или другими словами, все положительные числа.
• E(f) = (-3; 5].
  Т.е. от минус трех исключительно до пяти включительно.
• E(f) = (-∞; -7) ∪ [2; ∞).
  Т.е. от минус бесконечности до минус семи исключительно и от двух включительно до бесконечности.

Область значений функции

Время чтения: 40 минут

Область значений функции, ее свойства и примеры решения

В данном материалы мы подробно рассмотрим значение функции. Определим основные методы ее вычисления. Изучим множество значений функции.

Подробно, разберем на примерах, методы нахождения функции. Прежде, чем начать изучение материала, охарактеризуем основное определение значению функции.

Функция — это определенное соответствие между двумя множествами, каждому элементу значению первого множества соответствует только один элемент второго множества.

Функции удобно изображать в виде графических прямых или кривых.

Понятие области определения функции

Функция задается тогда, когда любому значению, например x соответствует любое значение y. Независимой переменной называют значение х или по другому аргументом. Числовое значение y, как правило является зависимой переменной.

Данная зависимость между x и y в алгебре называют функциональной. Записывают ее в виде функции y = f(x)

Другими словами, функция, это когда значения одной переменной зависят от значений другой переменной.

Далее можно сформулировать определение область функции. То есть, на какой промежуток действе функции распространяется.

Область функции можно выразить геометрически. Например, в виде графика. Где за основу берутся оси х и y.

Например:

Область значений функции y = z 2 — это все значения, которые будут больше либо равные нулю. В виде записи это выглядит следующим образом: f(у): у ≥ 0. Не все функции обозначаются одинаковыми формулировками, в основном D(f). Но тригонометрические функции обозначаются немного иначе. D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус. Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = x. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1]. Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.

Для указания множества чисел в определенном промежутке, необходимо выполнить следующие действия:

• назначается левая и правая границы, два числа через запятую или точку с запятой;
• ставится круглая или квадратная скобка; это зависит, входит ли граница в промежуток;
• круглая скобка, ставится, в том случае, если граница не входит в заданный промежуток;
• квадратная, в обратном случае.

Если у промежутка нет правой границы, записываем знак бесконечности или плюс бесконечности. Если отсутствует левая граница, записываем знак минус бесконечности.

В случае, если записывается множество, которое состоит из нескольких промежутков, ставится знак объединение.

Рассмотрим на примерах

Все действительные числа от 1 до 9, можно выразить в следующей записи. [1;9]

Все положительные числовые значения, имеют следующий вид: (0; +);

Так как ноль, не является положительным число, то возле него ставится круглая скобка.

Область значения и определения функции

Область определения — y(x) любые числовые значения аргумента x.

Чаще всего область определения выражают как функцию D(y).

В математике существует две главных запрещенных (недопустимых) операции:

• деление любого числового значения на ноль;
• извлечение квадратного корня, из числа, которое имеет отрицательное значение.

При определении области функции, вступают в силу два основных ограничения:

• В функции может быть деление на любую переменную. Таким образом, знаменатель, будет равен нулю и получим недопустимое значение. В таком случае, принято считать областью определения все действительные числа.
• Функция имеет действие: как извлечение квадратного корня. Подкоренное выражение обязательно не должно быть отрицательным. Множество решений этого неравенства и будет областью определения функции.

Область определения постоянной функции

Постоянная функция записывается обычной формулой y = N, а именно f(x) = N, где N — любое действительное число. Иными словами, принято называть константа.

Постоянная функция — это функция, при которой всегда наблюдается одно и то же числовое значение, независимо от того какое числовое значения имеет аргумент.

Область определения степенной функции

Степенная функция выглядит следующим образом: y = x k , то есть, f(x) = x k , где x — переменный показатель в основании степени, a — любое число в степени.

Область определения степенной функции, всегда имеет непосредственную зависимость, от значений показателя степени.

Рассмотрим основные моменты:

Если k — неотрицательное целое число, то областью определения данной функции является множество любых, обязательно, действительных чисел: (-∞, +∞).

Когда степенной показатель, является не целое число, то функция имеет следующий вид D(f) = [0, +∞).

Когда k — отрицательное целое число, то область определения функции представляет собой (-∞, 0) ∪ (0, +∞).

Для остальных действительных отрицательных, a область определения степенной функции — числовой промежуток (0, +∞).

Если k равно нулю, то функция определена для всех чисел, кроме нуля. Так как ноль нельзя возвести в степень, а любое другое число в нулевой степени равно 1.

То есть, при k = 0, y =x0 = 1, на заданной области определения (-∞, 0) ∪ (0, +∞).

Область определения показательной функции

Показательная функция записывается как: y=k x

где значение x — показатель степени;

k — число, которое обязательно больше нуля и не равно единице.

Область определения показательной функции — это множество значений R.

Основные примеры показательных функций:

Область определения, для этих функций, записывается следующим образом: (−∞, +∞).

Область определения логарифмической функции

Логарифмическая функция выражается как: y=log n k

Где значение n, имеет значение больше нуля и не менее единицы. Область определения логарифма и логарифмической функции — это множество положительных значений и действительных чисел.

Рассмотрим на примере, характер решения задачи данной функции.

Пример №1

y=ln x, определить область определения натурального логарифма. D(y)=(0;+).

На заданном интервале, производная будет иметь положительное значение, и функция будет возрастать на всем промежутке.

Определим односторонний предел при, стремлении аргумента к нулю и когда значение x стремится к бесконечности.

Из данного решения мы видим, что значения будут возрастать от минус бесконечности до плюс бесконечности.

Из этого следует, что множество всех действительных чисел – является областью значений функции натурального логарифма ln.

Ответ: множество всех действительных чисел, это и есть область значений функции ln.

Область определения и множество значений функций косинус, синус, тангенс, котангенс

Множество значений всех действительных чисел, будет являться областью определения функций синус и косинус, и записываться следующим образом.

Функции являются ограниченными, как сверху, так и снизу.

y = sin x и y = cos x

Промежуток их действия сводится к неравенству -1 ≤ y ≤ 1

Областью определения функции тангенс tg x, является выражение \[x \neq \frac<\pi><2>+\pi k, k \in z\].

Областью определения функции y = сtg x является множество чисел \[x \neq \frac<\pi><2>, k \in z\].

На нижеприведенных примерах подробно расписано решение задач, при определении области функции, при заданных промежутках значений.

Пример №1

Определить область значения функции sin x

Данный вид функции относится к категории периодической. Ее период равняется 2π

Определяем множество значений на следующем отрезке: (0;2π).

Пример №2

Необходимо определить область значения функции cos x.

Наименьшее значение равно -1;

Минимальное значение косинуса равняется -1, потому что наименьшее значение х, на окружности стремится к этому значению и, следовательно, равняется -1.

Максимальное значение косинуса будет соответственно 1. Поскольку значение на окружности х имеет число 1.

Область значение, следовательно, будет от минус одно до плюс одного. [-1;1].

Применяем двойное неравенство и записывает следующее выражение:

\[-1 \leq \cos 1 \leq 1\]

Область значения косинуса никогда не зависит от аргумента, только если сам аргумент выражен в виде сложного выражения. Где имеют место ограничения касающиеся области определения и области значения.

Таким образом, минимальное значение cos x, cos (15α), cos(5-11x) и так далее, будет однозначно равняться -1;

Самым максимальным значением cos x, cos(4φ), cos(5х+3) равняется 1.

Область значений функции y=cos x — также промежуток [-1;1].

Область значения квадрата косинуса, будет промежуток от нуля до единицы [0;1]. Потому что число в четной степени, является не отрицательным.

Аналогичным образом находим область значений модуля косинуса — промежуток [0;1]

\[0 \leq(\cos \alpha) \leq 1\]

Пример №3

y = tgx на определенном интервале \[\left(-\frac<\pi> <2>; \frac<\pi><1>\right)\].

Решение:

Из правил алгебры, известно, что производная тангенса имеет положительное значение. Соответственно функция будет иметь возрастающую характеристику.

Далее необходимо определить поведение функции, в заданных пределах.

Выполнив решение, мы получаем рост значений от минус до плюс бесконечности. Решение будет сводится к следующему: множество решение заданной функции, будет множество всех действий функции.

Пример №4

Решение:

Для всех значений x производная будет положительной, в пределах от -1;1

Следовательно, область значения арксинуса равняется:

Пример №5

Разберем функцию 2sinx2-4, где значение х меньше либо равно значению 3. Необходимо вычислить область значений.

Функция является для всех значений x определенной.

Наблюдаем недопустимый вид при значении аргумента − 3.

При приближении к данному аргументу функция стремится к \[-2 \sin \frac<3><2>-4\]. При стремлении x к − 3 с правой стороны значения будут стремиться к − 1.

Наблюдается разрыв в точке 3. Когда функция стремится к данному разрыву ее числовые значения приближаются к -1. Минус бесконечность будет наблюдаться при стремлении к такой точке, но только с правой стороны.

Из этого следует вся область значений данной функции разбивается на три интервала. (-;−3], (−3 ;3], (3;+)(-;-3], (-3; 3], (3;+).

Первый интервал имеет функцию, следующего вида \[y=2 \sin \frac<3><2>-4\]. Так как синус должен быть, меньше либо равен 1, или больше либо равен -1. Получаем следующие выражения:

\[-1 \leq \sin \frac<3> <2>\leq 1\] из этого следует \[-2 \leq 2 \sin \frac<3> <2>\leq 2 \Rightarrow-6 \leq 2 \sin \frac<3><2>-4 \leq-2\]

На промежутке -∞;-3, функция имеет следующие значения [-6;-2].

Функция y=-1, получается на полуинтервале (−3;3]. Следовательно, все значения будут сводится на данном интервале к одному числу, а именно -1.

Проанализируем второй промежуток (3;-+∞). Так как функция \[y=\frac<1>\] меньше нуля, она будет убывающей \[y=\frac<-1> <(x-) 2>

Если значение x больше значения 3, то большинство множеств функции будет в промежутке от нуля до +∞.