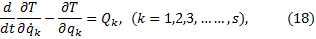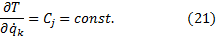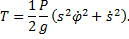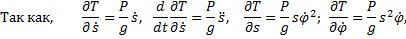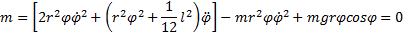Что такое обобщенная сила в уравнении лагранжа

УРАВНЕНИЯ ЛАГРАНЖА 2 РОДА. ОБОБЩЁННЫЕ КООРДИНАТЫ, СКОРОСТИ И СИЛЫ

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

УРАВНЕНИЯ ЛАГРАНЖА II РОДА.

ОБОБЩЁННЫЕ КООРДИНАТЫ,
СКОРОСТИ И СИЛЫ.
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
Динамика

Определять положение любой точки механической системы
Научиться описывать движение механической системы с несколькими степенями свободы

Цель введения обобщенных координат, скоростей и сил
2

Обобщенные координаты
Обобщенные координаты – это независимые между собой параметры любой размерности, однозначно определяющие положение механической системы в пространстве.
3
ОБОБЩЕННЫЕ КООРДИНАТЫ

ПОНЯТИЕ СТЕПЕНИ СВОБОДЫ
Число независимых между собой возможных перемещений МС называется числом степеней свободы системы.
4
У механической системы с голономными связями число обобщенных координат совпадает с числом её степеней свободы
Обобщенные координаты

В несвободной механической системе декартовых координат ее точек должны удовлетворять уравнениям связей, поэтому независимыми среди них будут только координат.
5
Если бы система была свободной, то все декартовых координат ее точек были бы независимыми.
КОЛИЧЕСТВО СТЕПЕНЕЙ СВОБОДЫ
Обобщенные координаты
1
2

6
КОЛИЧЕСТВО СТЕПЕНЕЙ СВОБОДЫ
Обобщенные координаты
У свободного твёрдого тела 6 степеней свободы:
3 поступательных вдоль осей координат и 3 вращательных вокруг этих осей.

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ТОЧЕК МС
Тогда радиус-векторы всех точек системы можно определить как функцию обобщенных координат
Обобщенные координаты будем обозначать буквой —
7
Обобщенные координаты

ОБОБЩЁННЫЕ СКОРОСТИ
Обобщенные скорости
8
При движении системы её обобщённые координаты будут меняться со временем по закону

— кинематическое уравнение движения в обобщённых координатах.

Размерность обобщённой скорости зависит от размерности соответствующей обобщённой координаты.
Производные от обобщённых координат по времени называются обобщёнными скоростями

ОБОБЩЁННЫЕ СИЛЫ
Обобщенные силы
9
Рассмотрим МС, состоящую из n материальных точек, на которые действуют силы
Пусть система имеет S степеней свободы и ее положение определяется обобщенными координатами
Сообщим системе такое независимое возможное перемещение, при котором координата получает приращение а остальные координаты не изменяются.
Тогда каждый из радиус-векторов точек системы получит элементарное приращение

ОБОБЩЁННЫЕ СИЛЫ
Обобщенные силы
10
Поскольку изменяется только координата , то вычисляется как частный дифференциал
Тогда вычислим сумму элементарных работ всех действующих сил на рассматриваемом перемещении.

ОБОБЩЁННЫЕ СИЛЫ
Обобщенные силы
11
— обобщённая сила, соответствующая координате

12
Обобщённые силы – это величины, равные коэффициентам при приращениях обобщённых
координат в выражении полной элементарной работы
действующих на систему сил.
Размерность обобщённой силы равна размерности работы, деленной на размерность соответствующей обобщённой координаты.
Обобщенные силы
Если системе сообщить такое возможное перемещение, при котором одновременно меняются все обобщенные координаты, то сумма элементарных работ приложенных сил на этом перемещении равна:

13
Обобщенные силы
ПРИМЕР (ДВОЙНОЙ МАЯТНИК)

13
Обобщенные силы
ПРИМЕР (ДВОЙНОЙ МАЯТНИК)

Курс повышения квалификации

Охрана труда

• Сейчас обучается 115 человек из 42 регионов

Курс профессиональной переподготовки

Охрана труда

• Сейчас обучается 233 человека из 54 регионов

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

• Сейчас обучается 351 человек из 63 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 582 221 материал в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Другие материалы

• 07.12.2020
• 100
• 0

• 27.10.2020
• 72
• 0

• 23.10.2020
• 86
• 0

• 16.10.2020
• 78
• 0

• 04.10.2020
• 93
• 0

• 22.09.2020
• 377
• 28

• 09.08.2020
• 121
• 0

• 21.07.2020
• 66
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 04.09.2020 367
• PPTX 281.9 кбайт
• 3 скачивания
• Оцените материал:

Настоящий материал опубликован пользователем Раджабова Патимат Рамазановна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 1 год и 1 месяц
• Подписчики: 0
• Всего просмотров: 22590
• Всего материалов: 226

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Рособрнадзор не планирует переносить досрочный период ЕГЭ

Время чтения: 0 минут

В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей

Время чтения: 1 минута

В Забайкалье в 2022 году обеспечат интернетом 83 школы

Время чтения: 1 минута

Минпросвещения упростит процедуру подачи документов в детский сад

Время чтения: 1 минута

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

РДШ организовало сбор гуманитарной помощи для детей из ДНР

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Теоретическая механика. Уравнения Лагранжа

В этой статье мы попробуем разобраться с такой темой, как «Уравнения Лагранжа». Вообще, уравнения Лагранжа довольно полезная штука, например, на их основе решаются задачи на малые колебания. В МГТУ им. Баумана в третьем семестре предлагается самостоятельное домашнее задание, в котором нужно записать уравнения Лагранжа для системы с двумя степенями свободы.

Итак, типовое задание выглядит так.

Прежде чем броситься решать эту задачу, посмотрим на задание и проанализируем его. Есть призма 3, которая движется поступательно по горизонтальной плоскости без трения. В призме сделан паз 2, по которому движется шарик 1. Если вы помните темы прошлого семестра, то легко увидите, что шарик совершает сложное движение — переносное поступательное вместе с призмой 3 и относительное поступательное по пазу 2. Далее есть стержень 4, который соединяет призму и каток 5. Очевидно, что скорость центра катка С равна скорость призмы. Каток движется без скольжения, это важный момент. Движение системы описывается двумя обобщенными координатами, которые любезно выбрал для нас составитель задания.

Итак, приступим к решению.

Поскольку обобщенных координат две (две степени свободы), система уравнений Лагранжа будет выглядеть так:

Расчет начинаем с записи уравнений связи — выражаем скорости всех ключевых точек и тел, имеющих массу, через обобщенные координаты. Из сказанного ранее понятно, что нам понадобится линейная скорость призмы 3, линейная скорость катка 5, угловая скорость катка 5 и скорость шарика 1. С поступательным движением все просто

С угловой скоростью катка тоже все понятно. Так как проскальзывание отсутствует

Самое трудное — выразить скорость шарика 1. Как мы уже говорили, он совершает сложное движение, значит, его скорость складывается из относительной и переносной. Переносная — это скорость поступательного движения призмы 3. Относительное — скольжение вдоль паза 2, которое описано координатой S. Значит

Векторно складываем эти две скорости

Второе выражение здесь — это теорема косинусов. Если нанести все векторы на рисунок, станет понятно, почему так.

Определившись со скоростями, записываем выражение для кинетической энергии системы Т. Полная кинетическая энергия складывается из кинетических энергий всех тел, обладающих массой. То есть в нашем случае, тел 1, 3, 5.

Шарик 1 обладает энергией

Призма 3 движется поступательно

Каток 5 совершает плоское движение, так что его кинетическая энергия складывается из энергии поступательного и вращательного движений

Полная кинетическая энергия системы

Для записи уравнений Лагранжа это выражение нужно несколько раз продифференцировать.

Сначала по координате x. Частные производные

Производную по x с точкой дифференцируем по времени

Теперь то же самое по координате S. Частные производные

Производная по времени

Левая часть уравнений Лагранжа готова. Займемся правой частью. Для нее нужно посчитать обобщенные силы по каждой координате. Есть несколько способов это сделать, мы предпочитаем делать это через элементарную работу на малом приращении координаты. В общем случае формула выглядит так

На практике это применяется следующим образом. Сначала нанесем на рисунок все действующие силы. В нашем случае это сила упругости пружины и силы тяжести.

Сначала считаем обобщенную силу по координате x. Для этого мысленно «замораживаем» координату S, и позволяем системе свободно двигаться по координате x. То есть шарик «приклеивается» к пазу 2, и внутри него никуда не движется. Все перемещение происходит по координате x. Очевидно, что сила упругости работу не совершает, так как ее длина не меняется. Очевидно, что силы тяжести работу не совершают, так как движение происходит горизонтально. Официальным языком это записывается так

Теперь обобщенная сила по координате S. Мысленно «замораживаем» координату x. Получается, что призма 3 вместе с пазом 2 и катком 5 стоит на месте, а внутри неподвижного паза движется шарик. Сила упругости совершает работу, также как и сила тяжести шарика 1. Пружина была растянута на величину статической деформации δ и дополнительно растянута на S в произвольный момент времени, то есть сила упругости равна с·(δ+S). Работа силы упругости отрицательна, так как пружина растягивается. Работа силы тяжести шарика 1 положительна, так как шарик движется вниз. Силы тяжести призмы 3 и катка 5 работу не совершают, так как эти тела покоятся. Получаем

Собственно, все. Собираем все посчитанные величины в уравнения Лагранжа и получаем систему дифференциальных уравнений, описывающих движение системы.

Для проверки можно посмотреть размерности, в обеих частях выражения размерности должны совпадать (обычно это ньютоны).

Конечно, разные задачи немного отличаются в ходе решения, но алгоритм всех задач примерно такой.

1) Определить число степеней свободы и выбрать обобщенные координаты

2) Записать уравнения связей

3) Записать выражение для кинетической энергии

4) Взять необходимые производные

5) Записать обобщенные силы по каждой координате

6) Записать уравнения Лагранжа

Если что-то не получается, не отчаивайтесь, мы всегда рады помочь.

Уравнения Лагранжа

По определению (7) и (12) обобщенные силы

Но на основании общего уравнения динамика (3), правая часть равенства равна нулю. И так как все (k = 1,2,3,…,s) отличны от нуля, то . Подставив значение обобщенной силы инерции (17), получим уравнение

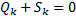
Эти уравнения называются дифференциальными уравнениями движения в обобщенных координатах, уравнениями Лагранжа второго рода или просто – уравнениями Лагранжа.

Количество этих уравнений равно числу степеней свободы материальной системы.

Если система консервативная и движется под действием сил потенциального поля, когда обобщенные силы 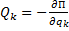, уравнения Лагранжа можно составить по форме

где L = T – П называется функцией Лагранжа (предполагается, что потенциальная энергия П не зависит от обобщенных скоростей).

Нередко при исследовании движения материальных систем оказывается, что некоторые обобщенные координаты q_j не входят явно в функцию Лагранжа (или в Т и П). Такие координаты называют циклическими. Уравнения Лагранжа, соответствующие этим координатам, получаются проще.

.

Первый интеграл таких уравнений находится сразу. Он называется циклическим интегралом:

Дальнейшие исследования и преобразования уравнений Лагранжа составляют предмет специального раздела теоретической механики – «Аналитическая механика».

Уравнения Лагранжа обладают целым рядом достоинств в сравнении с другими способами исследования движения систем. Основные достоинства: методика составления уравнений одинакова во всех задачах, реакции идеальных связей не учитываются при решении задач.

И еще одно – эти уравнения можно использовать для исследования не только механических, но и других физических систем (электрических, электромагнитных, оптических и др.).

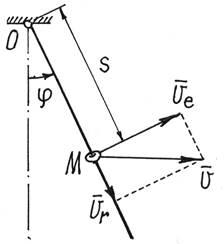
Пример 6. Продолжим исследование движение колечка М на качающемся стержне (пример 4).

Обобщенные координаты назначены – 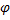и s (рис.13). Обобщенные силы определены: и .

Рис.13

Решение. Кинетическая энергия колечка Где а и .

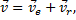
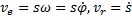
Составляем два уравнения Лагранжа

то уравнения получаются такими:

Получили два нелинейных дифференциальных уравнения второго порядка, для решения которых нужны специальные методы.

Пример 7. Составим дифференциальное уравнение движения балочки АВ, которая перекатывается без скольжения по цилиндрической поверхности (рис.14). Длина балочки АВ = l, вес – Р.

В положении равновесия балочка располагалась горизонтально и центр тяжести С ее находился на верхней точке цилиндра. Балочка имеет одну степень свободы. Положение ее определяется обобщенной координатой – углом 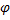(рис.76).

Рис.14

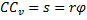
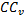
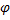
Решение. Система консервативная. Поэтому уравнение Лагранжа составим с помощью потенциальной энергии П=mgh, вычисленной относительно горизонтального положения. В точке касания находится мгновенный центр скоростей и ( равно длине дуги окружности с углом ).

Поэтому 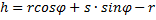(см. рис.76) и .

Кинетическая энергия (балка совершает плоскопараллельное движение)

Находим необходимые производные для уравнения и

Вопросы для самопроверки

— Что называется возможным перемещением несвободной механической системы?

— Как взаимосвязаны возможные и действительные перемещения системы?

— Какие связи называются: а) стационарными; б) идеальными?

— Сформулируйте принцип возможных перемещений. Запишите его формульное выражение.

— Возможно ли применение принципа виртуальных перемещений к системам с неидеальными связями?

— Что представляют собой обобщенные координаты механической системы?

— Чему равно число степеней свободы механической системы?

— В каком случае декартовы координаты точек системы зависят не только от обобщенных координат, но и от времени?

— Что называют возможными перемещениями механической системы?

— Зависят ли возможные перемещения от действующих на систему сил?

— Какие связи механической системы называют идеальными?

— Почему связь, осуществленная с трением, не является идеальной связью?

— Как формулируется принцип возможных перемещений?

— Какие виды может иметь уравнение работ?

— Почему принцип возможных перемещений упрощает вывод условий равновесия сил, приложенных к несвободным системам, состоящим из большого числа тел?

— Как составляются уравнения работ для сил, действующих на механическую систему с несколькими степенями свободы?

— Какова зависимость между движущей силой и силой сопротивления в простейших машинах?

— Как формулируется золотое правило механики?

— Каким образом определяют реакции связей с помощью принципа возможных перемещений?

— Какие связи называются голономными?

— Что называется числом степеней свободы механической системы?

— Что называется обобщенными координатами системы?

— Сколько обобщенных координат имеет несвободная механическая система?

— Сколько степеней свободы имеет управляемое колесо автомобиля?

— Что называется обобщенной силой?

— Запишите формулу, выражающую полную элементарную работу всех приложенных к системе сил в обобщенных координатах.

— Как определяется размерность обобщенной силы?

— Как вычисляются обобщенные силы в консервативных системах?

— Запишите одну из формул, выражающих общее уравнение динамики системы с идеальными связями. Каков физический смысл этого уравнения?

— Что называется обобщенной силой активных сил, приложенных к системе?

— Что такое обобщенная сила инерции?

— Сформулируйте принцип Даламбера в обобщенных силах.

— Какой вид имеет общее уравнение динамики?

— Что называется обобщенной силой, соответствующей некоторой обобщенной координате системы, и какую она имеет размерность?

— Чему равны обобщенные реакции идеальных связей?

— Выведите общее уравнение динамики в обобщенных силах.

— Какой вид имеют условия равновесия сил, приложенных к механической системе, полученные из общего уравнения динамики в обобщенных силах?

— Какими формулами выражаются обобщенные силы через проекции сил на неподвижные оси декартовых координат?

— Как определяются обобщенные силы в случае консервативных и в случае неконсервативных сил?

— Какие связи называются геометрическими?

— Приведите векторную запись принципа возможных перемещений.

— Назовите необходимое и достаточной условие равновесия механической системы с идеальными стационарными геометрическими связями.

— Каким свойством обладает силовая функция консервативной системы в состоянии равновесия?

— Запишите систему дифференциальных уравнений Лагранжа второго рода.

— Сколько уравнений Лагранжа второго рода можно составить для несвободной механической системы?

— Зависит ли число уравнений Лагранжа механической системы от количества тел, входящих в состав системы?

— Что называется кинетическим потенциалом системы?

— Для каких механических систем существует функция Лагранжа?

— Функцией каких аргументов является вектор скорости точки, принадлежащей механической системе с s степенями свободы?

— Чему равна частная производная от вектора скорости точки системы по какой-либо обобщенной скорости?

— Функцией каких аргументов является кинетическая энергия системы, подчиненной голономным нестационарным связям?

— Какой вид имеют уравнения Лагранжа второго рода? Чему равно число этих уравнений для каждой механической системы?

— Какой вид принимают уравнения Лагранжа второго рода в случае, когда на систему действуют одновременно консервативные и неконсервативные силы?

— Что представляет собой функция Лагранжа, или кинетический потенциал?

— Какой вид имеют уравнения Лагранжа второго рода для консервативной системы?

— В зависимости от каких переменных величин должна быть выражена кинетическая энергия механической системы при составлении уравнений Лагранжа?

— Как определяется потенциальная энергия механической системы, находящейся под действием сил упругости?