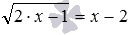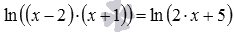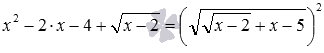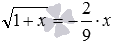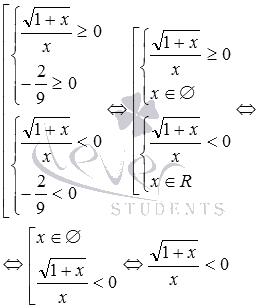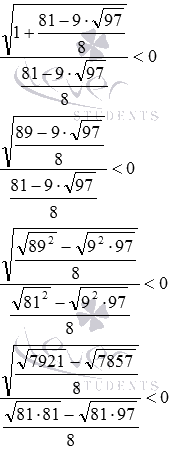Посторонние корни уравнения, отсеивание посторонних корней
Решение уравнений через переход к уравнениям-следствиям может привести к появлению так называемых посторонних корней. В этой статье мы, во-первых, детально разберем, что такое посторонние корни. Во-вторых, поговорим о причинах их возникновения. И в-третьих, на примерах рассмотрим основные способы отсеивания посторонних корней, то есть, проверки корней на предмет наличия среди них посторонних с целью исключения их из ответа.
Посторонние корни уравнения, определение, примеры
В школьных учебниках по алгебре не дается определение постороннего корня. Там представление о постороннем корне формируется путем описания следующей ситуации: при помощи некоторых преобразований уравнения осуществляется переход от исходного уравнения к уравнению-следствию, находятся корни полученного уравнения-следствия, и осуществляется проверка найденных корней подстановкой в исходное уравнение, которая показывает, что некоторые из найденных корней не являются корнями исходного уравнения, эти корни называют посторонними корнями для исходного уравнения [1, с. 174-175; 2, с. 202; 3, с. 187-188].
Отталкиваясь от этой базы, для себя можно принять такое определение постороннего корня:
Посторонние корни – это корни полученного в результате проведения преобразований уравнения-следствия, не являющиеся корнями исходного уравнения.
Приведем пример. Рассмотрим уравнение 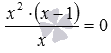
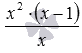
Причины возможного появления посторонних корней
Если для получения уравнения-следствия не использовать никакие «экзотические» преобразования, а использовать только основные преобразования уравнений, то посторонние корни могут возникнуть лишь по двум причинам:
- из-за расширения ОДЗ и
- из-за возведения обеих частей уравнения в одну и ту же четную степень.
Здесь стоит напомнить, что расширение ОДЗ в результате преобразования уравнения в основном происходит
- При сокращении дробей;
- При замене нулем произведения с одним или несколькими нулевыми множителями;
- При замене нулем дроби с нулевым числителем;
- При использовании некоторых свойств степеней, корней, логарифмов;
- При использовании некоторых тригонометрических формул;
- При умножении обеих частей уравнения на одно и то же выражение, обращающееся в нуль на ОДЗ для этого уравнения;
- При освобождении в процессе решения от знаков логарифмов.
Пример из предыдущего пункта статьи иллюстрирует появление постороннего корня из-за расширения ОДЗ, которое имеет место при переходе от уравнения 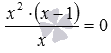
Также приведем пример появления постороннего корня из-за возведения обеих частей уравнения в одну и ту же четную степень. Иррациональное уравнение 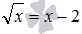
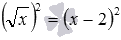
Заметим, что расширение ОДЗ и возведение обеих частей уравнения в одну и ту же четную степень, не всегда приводит к появлению посторонних корней. Например, при переходе от уравнения 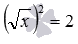
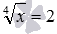
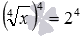
Что такое отсеивание посторонних корней?
Термин «отсеивание посторонних корней» лишь с натяжкой можно назвать устоявшимся, он встречается далеко не во всех учебниках алгебры, но является интуитивно понятным, из-за чего обычно и используется. Что понимают под отсеиванием посторонних корней, становится понятно из следующей фразы: «… проверка – обязательный этап решения уравнения, который поможет обнаружить посторонние корни, если они есть, и отбросить их (обычно говорят «отсеять»)» [1, с.176].
Отсеивание посторонних корней – это обнаружение и отбрасывание посторонних корней.
Теперь можно переходить к способам отсеивания посторонних корней.
Способы отсеивания посторонних корней
Проверка подстановкой
Основной способ отсеивания посторонних корней – это проверка подстановкой. Он позволяет отсеять посторонние корни, которые могли возникнуть и по причине расширения ОДЗ, и по причине возведения обеих частей уравнения в одну и ту же четную степень.
Проверка подстановкой состоит в следующем: найденные корни уравнения-следствия по очереди подставляются в исходное уравнение или в любое равносильное ему уравнение, те из них, которые дают верное числовое равенство, являются корнями исходного уравнения, а те, которые дают неверное числовое равенство или выражение, не имеющее смысла, являются посторонними корнями для исходного уравнения.
Покажем на примере, как проводится отсеивание посторонних корней через подстановку в исходное уравнение.
Решите уравнение
В некоторых случаях отсеивание посторонних корней целесообразнее проводить другими способами. Это относится в основном к тем случаям, когда проверка подстановкой связана со значительными вычислительными трудностями или когда стандартный способ решения уравнений какого-то определенного вида предполагает другой проверки (например, отсеивание посторонних корней при решении дробно-рациональных уравнений проводится по условию не равенства нулю знаменателя дроби). Разберем альтернативные способы отсеивания посторонних корней.
По ОДЗ
В отличие от проверки подстановкой, отсеивание посторонних корней по ОДЗ уместно не всегда. Дело в том, что этот способ позволяет отсеивать лишь посторонние корни, возникающие по причине расширения ОДЗ, и он не гарантирует отсеивание посторонних корней, которые могли возникнуть по другим причинам, например, из-за возведения обеих частей уравнения в одну и ту же четную степень. Более того, не всегда просто отыскать ОДЗ для решаемого уравнения. Тем не менее, способ отсеивания посторонних корней по ОДЗ стоит держать на вооружении, так как часто его использование требует меньших вычислительных работ, чем использование других способов.
Отсеивание посторонних корней по ОДЗ проводится следующим образом: все найденные корни уравнения-следствия проверяются на предмет принадлежности области допустимых значений переменной для исходного уравнения или любого равносильного ему уравнения, те из них, которые принадлежат ОДЗ, являются корнями исходного уравнения, а те из них, которые не принадлежат ОДЗ, являются посторонними корнями для исходного уравнения.
Анализ приведенной информации приводит к выводу, что отсеивание посторонних корней по ОДЗ целесообразно проводить, если единовременно:
- легко находится ОДЗ для исходного уравнения,
- посторонние корни могли возникнуть только по причине расширения ОДЗ,
- проверка подстановкой связана со значительными вычислительными сложностями.
Покажем, как проводится отсеивание посторонних корней, на практике.
Решите логарифмическое уравнение
По условиям ОДЗ
Как мы сказали в предыдущем пункте, если посторонние корни могли возникнуть лишь по причине расширения ОДЗ, то их можно отсеять по ОДЗ для исходного уравнения. Но не всегда просто найти ОДЗ в виде числового множества. В таких случаях можно проводить отсеивание посторонних корней не по ОДЗ, а по условиям, определяющим ОДЗ. Разъясним, как проводится отсеивание посторонних корней по условиям ОДЗ.
Найденные корни по очереди подставляются в условия, определяющие ОДЗ для исходного уравнения или любого равносильного ему уравнения. Те из них, которые удовлетворяют всем условиям, являются корнями уравнения. А те из них, которые не удовлетворяют хотя бы одному условию или дают не имеющее смысла выражение, являются посторонними корнями для исходного уравнения.
Приведем пример отсеивания посторонних корней по условиям ОДЗ.
Решить иррациональное уравнение
Отсеивание посторонних корней, возникающих из-за возведения обеих частей уравнения в четную степень
Понятно, что отсеивание посторонних корней, возникающих из-за возведения обеих частей уравнения в одну и ту же четную степень, можно осуществить путем подстановки в исходное уравнение или в любое равносильное ему уравнение. Но такая проверка может быть связана со значительными вычислительными трудностями. На этот случай стоит знать альтернативный способ отсеивания посторонних корней, о котором мы сейчас и поговорим.
Отсеивание посторонних корней, которые могут возникнуть при возведении в одну и ту же четную степень обеих частей иррациональных уравнений вида 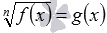
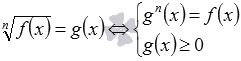
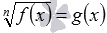
Покажем, как на практике отсеиваются посторонние корни указанным способом.
Решите уравнение
В заключение скажем, что рассмотренный подход является частным случаем более общего подхода к отсеиванию посторонних корней, возникающих при возведении обеих частей уравнения в одну и ту же четную степень. Отсеять посторонние корни, которые могут возникнуть при возведении обеих частей уравнения f(x)=g(x) в одну и ту же четную степень, можно по условию 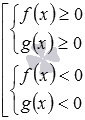
Приведем пример отсеивания посторонних корней предложенным способом. Возьмем уравнение 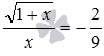
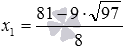

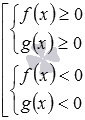
Подстановка в неравенство 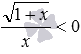
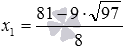
Полученное неравенство верное, так как в числителе положительное число, а в знаменателе – отрицательное, поэтому, отношение этих чисел есть отрицательное число. Значит, 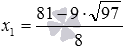
Подстановка в неравенство 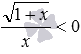

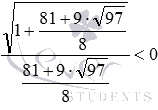

Посторонние и потерянные корни.
статья по алгебре (9, 10, 11 класс)
Комплекс уравнений, при решении которых выполняются тождественные преобразования, приводящие к появлению посторонних корней или их потере.
Скачать:
| Вложение | Размер |
|---|---|
| postoronnie_i_poteryannye_korni.doc | 194.5 КБ |
Предварительный просмотр:
Посторонние и потерянные корни.
при решении которых выполняются тождественные преобразования, приводящие к появлению посторонних корней или их потере.
Рассмотрим несколько конкретных примеров, где некоторые преобразования уравнений приводят к новым уравнениям, неравносильным данному, что ведёт к появлению посторонних корней или их потере.
Дано уравнение 3х(х – 1) = 5(х – 1).
1 способ решения:
Раскроем скобки в данном уравнении, перенесём все члены в левую часть и решим квадратное уравнение.
Корни уравнения х = 1, х = .
2 способ решения:
Сократить обе части уравнения на общий множитель (х – 1), то получится уравнение
3х = 5, которое имеет всего лишь один корень х = .
Таким образом, деление обеих частей уравнения на множитель, содержащий неизвестное, может привести к потере корней.
Дано уравнение 2х -3 = 5 .
Данное уравнение имеет единственный корень х = 4.
Возведём обе части этого уравнения в квадрат, получим (2х – 3)² = 25.
Решая это уравнение, найдём корни: х = -1, х = 4.
Новое уравнение(2х – 3)² = 25 неравносильно исходному уравнению 2х – 3= 5.
Корень х = -1 не является корнем исходного уравнения, следовательно, является посторонним корнем.
Посторонний корень может появиться при возведении обеих частей уравнения в квадрат, вообще в чётную степень .
Сократим дробь, стоящую в левой части уравнения на х и получим уравнение
Решим данное уравнение: х = 0 или х – 1= 0
т.е. корни данного уравнения 0 и 1.
Корнем исходного уравнения 0 не является, так как в исходном уравнении придётся делить на ноль, а так как на 0 делить нельзя, то х = 0 — посторонний корень.
Посторонний корень может появиться при сокращении дроби на выражение, содержащее неизвестное.
Возведём обе части уравнения в квадрат (возведение в чётную степень)
х = 5 – посторонний корень
Так как уравнение f²(х) = g²(х) является уравнением — следствием не только для уравнения
f(х) = g(х), но и для уравнения f(х) = — g(х). Поэтому при возведении в квадрат корни не теряются, но посторонние корни появиться могут. Уравнения не равносильны, но они равносильны на области определения: х 2.
Уравнение исходное можно заменить на равносильную систему
При решении иррациональных уравнений надо делать проверку подстановкой корней в исходное уравнение или использовать ОDЗ в зависимости от того, где вычисления выполняются легче.
Возведём обе части уравнения в квадрат.
2х – 1 — х² + 4х – 4 = 0
1 = — 1 – неверное 3 = 3 – верное
х = 1 – посторонний корень х = 5 – корень
Возведём обе части уравнения в квадрат (возведение в чётную степень).
х = х =
Проверка подстановкой в данном случае будет сопровождаться значительными трудностями при вычислении, поэтому прибегнем к использованию ОDЗ:
Из уравнения = — х — х 0
Подставим в данное неравенство полученные корни.
1) х = Имеем: — · 0 – неверное, т.к. произведение положительного и отрицательного числа отрицательно. Значит, х = — посторонний корень.
2) х = . Имеем: — · 0 – верное, т.к. произведение двух отрицательных чисел положительно. Значит, х =
— корень уравнения.
Ответ: .
Посторонние корни могут появиться также при умножении обеих частей уравнения на множитель, содержащий неизвестное, если этот множитель при действительных значениях х обращается в нуль.
+ = |• (х-1).(х-2) 0
Умножим обе части уравнения на наименьший общий знаменатель дробей, не равный нулю.
1 + 3х – 6 = — х ² + 4х -3
Проверку в дробно – рациональных уравнениях делаем по условию неравенства нулю знаменателя, проверяем условие (х-1).(х-2) 0
(-1 – 1)(-1 – 2) 0 (2 -1 )(2 – 2) 0
6 0- верное 0 0 – неверное
х — корень уравнения х — посторонний корень
Причиной изменения множества корней уравнения во время его преобразования является применение равенств, правая и левая части которых имеют разные области определения. Вот некоторые из них:
• log (х·у) = log х + log у
В каждом из этих равенств область определения выражения, стоящего в правой части, является подмножеством области выражения, стоящего в левой части. Поэтому использование этих равенств слева направо может привести к потере корней, а справа налево – к появлению посторонних корней.
log (х – 2) + log
(х+3) = 2
По свойству логарифмов имеем:
log (х – 2)(х + 3) = 2
х =6 и х =-7 х = -7 – посторонний корень
Исходное и последнее уравнения неравносильны в ОDЗ
Чтобы исключить посторонний корень надо использовать ОDЗ или уравнение заменить равносильной системой
3sinx + 4 cos x = 5
х = 2arctg + 2 , n
При переходе от уравнения (1) к уравнению(2) могла произойти потеря корней, значит необходимо проверить, являются ли корни уравнения cos =0 корнями данного уравнения.
Если х = , n ,тогда 3sin( ) + 4cos ( ) = 5, х
0 + 4(-1) = 5 – не верно, значит х = , n , не является корнями исходного уравнения.
Ответ: х = 2arctg + 2 , n
Итак, в процессе решения каждое уравнение заменялось на какое-то новое, а у нового уравнения естественно могут быть свои корни. Проследить за изменением корней, не допустить их потери и отбросить лишние корни – это и есть задача правильного решения уравнений.
По теме: методические разработки, презентации и конспекты
Выход из одиночества…Урок внеклассного чтения в 10 классе. (Экзистенциальное восприятие мира в повести А. Камю «Посторонний»)
«Посторонний» – яркий пример экзистенциализма, основным критерием которого является п.
Типичные ошибки в решении задания С1(потеря корней, появление «посторонних» корней)
В презентации для подготовки к ЕГЭ по математике представлены решения двух заданий (тригонометрических уравнений), где подробно рассмотрены возможности появления посторонних корней и потери корн.
Самостоятельная работа на тему «Комплекс уравнений, при решении которых выполняется тождественные преобразования, приводящие к появлению посторонних корней или их потере, с анализом процесса решения»
Вашему вниманию предлагаю самостоятельную работу на тему «Комплекс уравнений, при решении которых выполняется тождественные преобразования, приводящие к появлению посторонних корней или их.
ПРАВИЛА пребывания на территории школы посторонних лиц
Летний оздоровительный лагерь «Зеленая планета», июнь 2017г.
Конспект мероприятия «Конкурс рисунков на асфальте «Добро пожаловать. Или посторонним вход воспрещён», посвящённого Дню солидарности в борьбе с терроризмом.
Занятие рекомендуется проводить с детьми младшего школьного возраста.Занятие проводится в форме доверительной беседы взрослого и детей. При этом взрослый должен не напугать детей, не научить их видеть.
Самостоятельная работа «Комплекс уравнений, при решении которых выполняется тождественные преобразования, приводящие к появлению посторонних корней или их потере, с анализом процесса решения»
Работа в помощь слушателям курсов преподавания алгебры.
Статья «Координаты счастья героев А.Камю (по повести «Посторонний»)»
Что есть счастье? «Чувство и состояние полного, высшего удовлетворения», как диктуется в толковом словаре. Чаще всего оно заметно по сверкающим глазам и искренней улыбке. Но возможно ли сч.
Рациональные уравнения. Посторонний корень
Рациональные уравнения – это уравнения, в которых и левая и правая части – рациональные выражения. Рациональное уравнение называется целым, или алгебраическим, если в нем нет деления на выражение, содержащее переменную. Решением, или корнем уравнения, называется всякое значение неизвестного х, при подстановке которого в обе части уравнения получается истинное числовое равенство. Решить уравнение – значит найти все его корни или доказать, что корней нет.
Если в результате преобразований мы заменим исходное уравнение следствием, то при решении нового уравнения мы можем получить корни, не являющиеся корнями исходного уравнения, т. е. посторонние корни. Однако, это не страшно, так как от посторонних корней, как правило, можно легко избавиться с помощью проверки.
Дробно-рациональные уравнения
Если в рациональном уравнении есть деление на выражение, содержащее переменную, то уравнение называется дробно-рациональным.
Решение дробно-рационального уравнения сводится в конечном итоге к замене исходного уравнения целым уравнением, которое равносильно исходному уравнению или является его следствием.
При решении дробного уравнения целесообразно поступать следующим образом:
- определить область допустимых значений переменной х (ОДЗ);
- найти наименьший общий знаменатель дробей, входящих в уравнение;
- умножить обе части уравнения на общий знаменатель и привести подобные;
- решить получившееся целое уравнение.
Пример. Решить уравнение: \(\frac
Решение: В самом начале перенесем все слагаемые в левую сторону, чтобы справа остался 0. Получаем:
Теперь приведем левую часть уравнения к общему знаменателю:
Данное уравнение эквивалентно системе: \(\begin
Первое уравнение системы – это квадратное уравнение.
Вычисляем дискриминант: \(D=b^2-4ac=(-5)^2-4\cdot1\cdot6=25-24=1=1^2\) .
Далее, по формуле корней квадратного уравнения находим:
Теперь решим второе неравенство: произведение множителей не равно 0 тогда и только тогда, когда ни один из множителей не равен 0.
Необходимо, чтобы выполнялись два условия: \(\begin
Получаем, что из двух корней первого уравнения подходит только один – 3.
Лыжнику необходимо было пробежать расстояние в 50 км. Начав бег на 30 мин позже назначенного срока, лыжник бежал со скоростью, больше предполагавшейся на 5 км/ч, и прибежал к месту назначения вовремя. Определите скорость, с которой бежал лыжник.
Две бригады должны были собрать весь урожай за 16 дней. Однако после четырех дней совместной работы первая бригада была переведена на другую работу, и оставшуюся часть работы вторая бригада завершила за 18 дней. За сколько дней вторая бригада в отдельности собрала бы весь урожай?
Турист прошел по проселочной дороге \(6\) км и по шоссе \(3\) км, затратив на весь путь \(2\) ч. По шоссе он прошел со скоростью на \(2\) км/ч больше, чем по проселочной дороге. С какой скоростью шел турист по проселочной дороге?
http://nsportal.ru/shkola/algebra/library/2019/02/21/postoronnie-i-poteryannye-korni
http://itest.kz/ru/ent/matematika/8-klass/lecture/racionalnye-uravneniya-postoronnij-koren