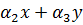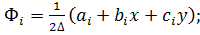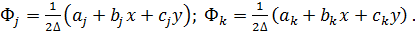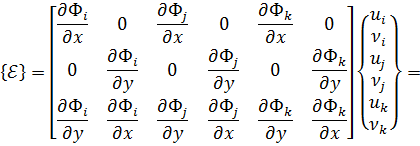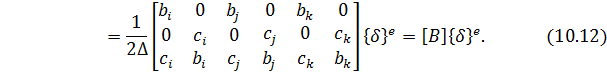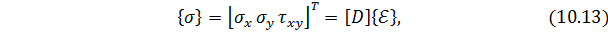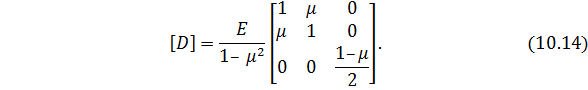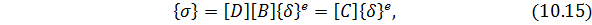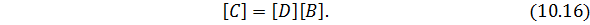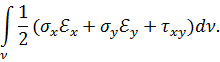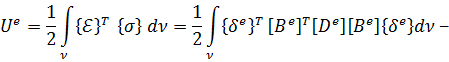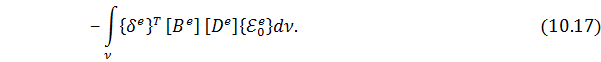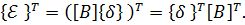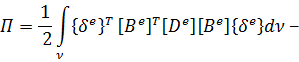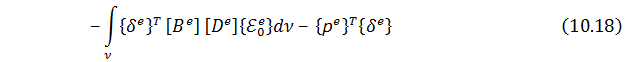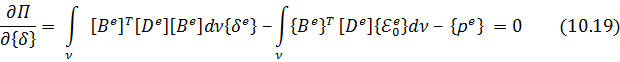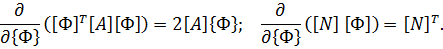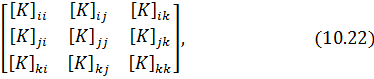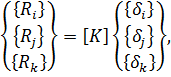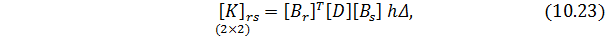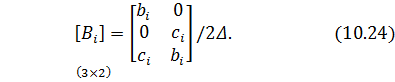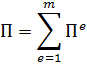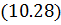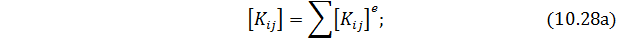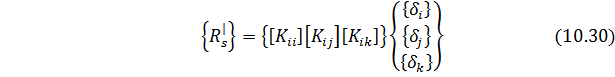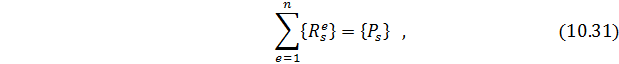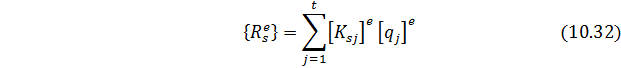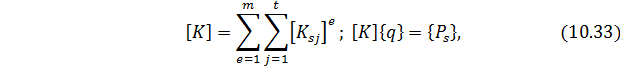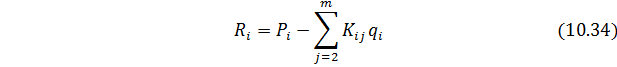Системы уравнений: определение, виды, примеры решения
Статья знакомит с таким понятием, как определение системы уравнений и ее решением. Будут рассмотрены часто встречающиеся случаи решений систем. Приведенные примеры помогут подробно пояснить решение.
Определение системы уравнений
Чтобы перейти к определению системы уравнений, необходимо обратить внимание на два момента: вид записи и ее смысл. Чтобы понять это, нужно подробно остановиться на каждом из видов, тогда сможем прийти к определению систем уравнений.
Например, возьмем два уравнения 2 · x + y = − 3 и x = 5 , после чего объединим фигурной скобкой такого плана:
2 · x + y = — 3 , x = 5 .
Уравнения, объединенные фигурной скобкой, считаются записями систем уравнений. Они задают множества решений уравнений данной системы. Каждое решение должно являться решением всех заданных уравнений.
Другими словами это означает, что любые решения первого уравнения будут решениями всех уравнений, объединенных системой.
Системы уравнений – это некоторое количество уравнений, объединенных фигурной скобкой, имеющих множество решений уравнений, которые одновременно являются решениями для всей системы.
Основные виды систем уравнений
Видов уравнений достаточно много, как систем уравнений. Для того, чтобы было удобно решать и изучать их, подразделяют на группы по определенным характеристикам. Это поможет в рассмотрении систем уравнений отдельных видов.
Для начала уравнения классифицируются по количеству уравнений. Если уравнение одно, то оно является обычным уравнением, если их более, тогда имеем дело с системой, состоящей из двух или более уравнений.
Другая классификация затрагивает число переменных. Когда количество переменных 1 , говорят, что имеем дело с системой уравнений с одной неизвестной, когда 2 – с двумя переменными. Рассмотрим пример
x + y = 5 , 2 · x — 3 · y = 1
Очевидно, что система уравнений включает в себя две переменные х и у .
При записи таких уравнений считается число всех переменных, имеющихся в записи. Их наличие в каждом уравнении необязательно. Хотя бы одно уравнение должно иметь одну переменную. Рассмотрим пример системы уравнений
2 x = 11 , x — 3 · z 2 = 0 , 2 7 · x + y — z = — 3
Данная система имеет 3 переменные х , у , z . Первое уравнение имеет явный х и неявные у и z . Неявные переменные – это переменные, имеющие 0 в коэффициенте. Второе уравнение имеет х и z , а у неявная переменная. Иначе это можно записать таким образом
2 x + 0 · y + 0 · z = 11
А другое уравнение x + 0 · y − 3 · z = 0 .
Третья классификация уравнений – это вид. В школе проходят простые уравнения и системы уравнений, начиная с систем двух линейных уравнений с двумя переменными. Имеется в виду, что система включает в себя 2 линейных уравнения. Для примера рассмотрим
2 · x — y = 1 , x + 2 · y = — 1 и — 3 · x + y = 0 . 5 , x + 2 2 3 · y = 0
Это основные простейшие линейные уравнения. Далее можно столкнуться с системами, содержащими 3 и более неизвестных.
В 9 классе решают уравнения с двумя переменными и нелинейные. В целых уравнениях повышается степень для увеличения сложности. Такие системы называют системами нелинейных уравнений с определенным количеством уравнений и неизвестных. Рассмотрим примеры таких систем
x 2 — 4 · x · y = 1 , x — y = 2 и x = y 3 x · y = — 5
Обе системы с двумя переменными и обе являются нелинейными.
При решении можно встретить дробно-рациональные уравнения. Например
x + y = 3 , 1 x + 1 y = 2 5
Могут называть просто системой уравнений без уточнения, каких именно. Редко уточняют сам вид системы.
Старшие классы переходят к изучению иррациональных, тригонометрических и показательных уравнений. Например,
x + y — x · y = 5 , 2 · x · y = 3 , x + y = 5 · π 2 , sin x + cos 2 y = — 1 , y — log 3 x = 1 , x y = 3 12 .
Высшие учебные заведения изучают и исследуют решения систем линейных алгебраических уравнений (СЛАУ). Левая часть таких уравнений содержит многочлены с первой степенью, а правая – некоторые числа. Отличие от школьных в том, что количество переменных и количество уравнений может быть произвольным, чаще всего несовпадающим.
Решение систем уравнений
Решение системы уравнений с двумя переменными – это пара переменных, которая при подстановке обращает каждое уравнение в верное числовое неравенство, то есть является решением для каждого уравнения данной системы.
К примеру, пара значений х = 5 и у = 2 являются решением системы уравнений x + y = 7 , x — y = 3 . Потому как при подстановке уравнения обращаются в верные числовые неравенства 5 + 2 = 7 и 5 − 2 = 3 . Если подставить пару х = 3 и у = 0 , тогда система не будет решена, так как подстановка не даст верное уравнение, а именно, мы получим 3 + 0 = 7 .
Сформулируем определение для систем, содержащих одну и более переменных.
Решение системы уравнений с одной переменной – это значение переменной, которая является корнем уравнений системы, значит, все уравнения будут обращены в верные числовые равенства.
Рассмотрим на примере системы уравнений с одной переменной t
t 2 = 4 , 5 · ( t + 2 ) = 0
Число — 2 – решение уравнения, так как ( − 2 ) · 2 = 4 , и 5 · ( − 2 + 2 ) = 0 являются верными числовыми равенствами. При t = 1 система не решена, так как при подстановке получим два неверных равенства 12 = 4 и 5 · ( 1 + 2 ) = 0 .
Решение системы с тремя и более переменными называют тройку, четверку и далее значений соответственно, которые обращают все уравнения системы в верные равенства.
Если имеем значения переменных х = 1 , у = 2 , z = 0 , то подставив их в систему уравнений 2 · x = 2 , 5 · y = 10 , x + y + z = 3 , получим 2 · 1 = 2 , 5 · 2 = 10 и 1 + 2 + 0 = 3 . Значит, эти числовые неравенства верные. А значения ( 1 , 0 , 5 ) не будут решением, так как, подставив значения, второе из них будет неверное, как и третье: 5 · 0 = 10 , 1 + 0 + 5 = 3 .
Системы уравнений могут не иметь решений вовсе или иметь бесконечное множество. В этом можно убедиться при углубленном изучении данной тематики. Можно прийти к выводу, что системы уравнений – это пересечение множеств решений всех ее уравнений. Раскроем несколько определений:
Несовместной называют систему уравнений, когда она не имеет решений, в противном случае ее называют совместной.
Неопределенной называют систему, когда она имеет бесконечное множество решений, а определенной при конечном числе решений либо при их отсутствии.
Такие термины редко применяются в школе, так как рассчитаны для программ высших учебных заведений. Знакомство с равносильными системами углубит имеющиеся знания по решению систем уравнений.
Как решать систему уравнений
О чем эта статья:
8 класс, 9 класс, ЕГЭ/ОГЭ
Основные понятия
Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.
Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.
Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.
Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.
Линейное уравнение с двумя переменными
Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.
Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.
Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.
Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:
Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.
Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.
Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).
Провести прямую через эти две точки и вуаля — график готов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Система двух линейных уравнений с двумя переменными
Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.
Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:
Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.
Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.
Можно записать систему иначе:
Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.
Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.
Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.
Метод подстановки
Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:
Выразить одну переменную через другую из более простого уравнения системы.
Подставить то, что получилось на место этой переменной в другое уравнение системы.
Решить полученное уравнение, найти одну из переменных.
Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.
Записать ответ. Ответ принято записывать в виде пар значений (x; y).
Потренируемся решать системы линейных уравнений методом подстановки.
Пример 1
Решите систему уравнений:
x − y = 4
x + 2y = 10
Выразим x из первого уравнения:
x − y = 4
x = 4 + y
Подставим получившееся выражение во второе уравнение вместо x:
x + 2y = 10
4 + y + 2y = 10
Решим второе уравнение относительно переменной y:
4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2
Полученное значение подставим в первое уравнение вместо y и решим уравнение:
x − y = 4
x − 2 = 4
x = 4 + 2
x = 6
Ответ: (6; 2).
Пример 2
Решите систему линейных уравнений:
x + 5y = 7
3x = 4 + 2y
Сначала выразим переменную x из первого уравнения:
x + 5y = 7
x = 7 − 5y
Выражение 7 − 5y подставим вместо переменной x во второе уравнение:
3x = 4 + 2y
3 (7 − 5y) = 4 + 2y
Решим второе линейное уравнение в системе:
3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1
Подставим значение y в первое уравнение и найдем значение x:
x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2
Ответ: (2; 1).
Пример 3
Решите систему линейных уравнений:
x − 2y = 3
5x + y = 4
Из первого уравнения выразим x:
x − 2y = 3
x = 3 + 2y
Подставим 3 + 2y во второе уравнение системы и решим его:
5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1
Подставим получившееся значение в первое уравнение и решим его:
x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1
Ответ: (1; −1).
Метод сложения
Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:
При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.
Складываем почленно левые и правые части уравнений системы.
Решаем получившееся уравнение с одной переменной.
Находим соответствующие значения второй переменной.
Запишем ответ в в виде пар значений (x; y).
Система линейных уравнений с тремя переменными
Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:
Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).
Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.
Решение задач
Разберем примеры решения систем уравнений.
Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?
5x − 8y = 4x − 9y + 3
5x − 8y = 4x − 9y + 3
5x − 8y − 4x + 9y = 3
Задание 2. Как решать систему уравнений способом подстановки
Выразить у из первого уравнения:
Подставить полученное выражение во второе уравнение:
Найти соответствующие значения у:
Задание 3. Как решать систему уравнений методом сложения
- Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:
- Решаем полученное квадратное уравнение любым способом. Находим его корни:
- Найти у, подставив найденное значение в любое уравнение:
- Ответ: (1; 1), (1; -1).
Задание 4. Решить систему уравнений
Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.
Задание 5. Как решить систему уравнений с двумя неизвестными
При у = -2 первое уравнение не имеет решений, при у = 2 получается:
Лекция 10. Метод конечных элементов. Плоская задача.
10.1. Содержание метода.Метод конечных элементов (МКЭ) представляет
собой эффективный численный метод решения инженерных и физических задач. Он широко применяется при проектировании судов, летательных аппаратов, несущих систем многоэтажных зданий и т.п. Для МКЭ характерна ясная физическая трактовка. Его можно рассматривать, в частности, как обобщение классического метода строительной механики – метода перемещений. С другой стороны, МКЭ является своеобразной формой часто применяемого вариационного метода Ритца. Различие между традиционной формой метода Ритца и МКЭ состоит в выборе системы координатных функций. Если в методе Ритца функции (обычно ряды) задаются для всей области, то в МКЭ они задаются для ее частей и через множество этих функций определяется состояние системы.
Классический подход к задаче об изучении напряженно-деформированного состояния диска предполагает изучение бесконечно малого его элемента. Получающиеся при этом дифференциальные уравнения в частных производных (равновесия и геометрические) совместно с физическими уравнениями и контурными условиями позволяют определить напряжения, деформации и перемещения в каждой точке диска.
МКЭ предполагает иной подход. Рассматривается элемент конечных размеров (КЭ), за счет чего осуществляется переход от сплошной системы с бесконечным числом степеней свободы, к системе с конечным числом степеней свободы.
Разделим воображаемыми линиями диск в условиях плоской задачи на некоторое количество элементов конечных размеров, например, треугольной формы и примем за узловые точки их вершины. Очевидно, что если диск находится в равновесии то и его элемент, определенный узлами i, j, k, под воздействием напряжений (усилий) от смежных элементов, также уравновешен. Приложим затем к этому элементу вместо фактических усилий, действующих вдоль его граней, статически эквивалентные узловые силы, т.е. силы, вызывающие внутри элемента действительное напряженно- деформированное состояние.
Поставив в соответствие каждому узловому усилию узловое перемещение, представим сплошной диск набором конечных элементов (КЭ), взаимодействующих между собой в конечном числе узловых точек.
Такой подход позволяет в дальнейшем использовать один из классических методов строительной механики, например метод перемещений (возможно также применение метода сил, либо смешанного). Для этого необходимо установить матрицы жесткости всех КЭ и, из условия равновесия узлов, получить разрешающие уравнения задачи. Найденные узловые перемещения не дают полной характеристики напряженно-деформированного состояния диска. Необходим переход от этих величин к перемещениям, напряжениям и деформациям внутри конечных элементов, т.е. речь идет о решении плоской задачи для каждого КЭ, находящегося под воздействием узловых перемещений. Такой переход в МКЭ осуществляется приближенно, путем задания интерполяционных (координатных) функций (функций формы), что и делает метод приближенным. Функции эти (обычно полиномы) такие, что обеспечивают неразрывность перемещений при переходе от одного элемента к другому. Функции формы однозначно определяют перемещения внутри элемента через узловые перемещения.
Естественно, что при реализации МКЭ возникает необходимость приведения действующих на конструкцию нагрузок к сосредоточенным узловым силам.
Обычно все зависимости, связанные с КЭ , строятся в местной системе координат, с последующим переходом в общую систему для всей области. Это позволяет заранее получить необходимые соотношения для часто применяемых типов КЭ.
Алгоритм решения задач по МКЭ содержит следующие этапы:
1. Дискретизация — разбиение заданной области на КЭ; нумерация узлов и КЭ.
2. Аппроксимация перемещений узлов в КЭ.
3. Построение матриц жесткости (МЖ) конечных элементов.
4. Построение глобальной матрицы жесткости общей системы уравнений.
5. Сведение нагрузок и воздействий, приложенных к КЭ, к узловым силам, учет условий закрепления.
6. Решение общей системы уравнений.
7. Определение напряжений и (при необходимости) деформаций в КЭ.
Дискретизация области.Разбиение области на подобласти представляет собой первый шаг на пути к решению задачи, и именно этот шаг не имеет теоретического обоснования. Искусство разбиения области зависит от имеющихся инженерных навыков. Плохое или несовершенное разбиение будет приводить к ошибочным результатам, если даже остальные этапы метода осуществляются с достаточной точностью.
Дискретизация области ( тела ) включает задание числа, размеров и формы подобластей, которые используются для построения дискретной модели реального тела. При этом, с одной стороны, элементы должны быть выбраны достаточно малыми, чтобы получить приемлемые результаты, а с другой стороны, применение достаточно крупных элементов сокращает вычислительную работу.
При решении задач по МКЭ используются элементы различных типов, в основном трехузловые треугольные КЭ, как наиболее простые и чаще других применяемые для решения плоской задачи.
Разбиение области на элементы.Процесс дискретизации может быть разделен на 2 этапа: разбиение тела на элементы и нумерация элементов и узлов. При разбиении любой двумерной области на элементы сначала тело делится на четырехугольные и треугольные подобласти или зоны, которые затем подразделяются на треугольники. Границы между подобластями должны проходить там, где изменяются геометрия, приложенная нагрузка или свойства элементов.
Наиболее просто можно разбить треугольную подобласть на элементы, если выбрать определенное число узлов вдоль каждой стороны, соединить соответствующие узлы прямыми линиями и точки пересечений этих линий считать узлами.
Четырехугольные зоны обычно разбивают на элементы соединением узлов на противоположных сторонах. Пересечения линий определяют внутренние узловые точки. Внутренние четырехугольники могут расматриваться как элементы или могут быть разбиты на треугольные элементы проведением короткой диагонали в каждом внутреннем четырехугольнике.
Треугольная и четырехугольная зоны могут иметь общую границу. Число узлов на этой границе для обеих зон должно быть одинаковым и относительное положение узлов должно совпадать.
В задачах МДТТ необходимо отметить узлы, которые имеют известные перемещения. Для обозначения неподвижных узлов применяется символ неподвижного шарнира. Если узел может перемещаться только в одном направлении, используется символ подвижного шарнира. Учет узловых условий такого типа осуществляется путем видоизменения общей системы уравнений, решение которой определяет узловые перемещения.
Нумерация узлов. Нумерация узлов влияет на эффективность вычислений, необходимых для получения решения. Использование МКЭ приводит к системе линейных алгебраических уравнений, большее число коэффициентов которой равно нулю. Рассмотрение матрицы коэффициентов системы показывает, что все ненулевые коэффициенты и некоторые нулевые находятся между двумя линиями, параллельными главной диагонали. Расстояние между главной диагональю и этими линиями называется шириной полосы матрицы. Все коэффициенты вне этой полосы равны нулю и они не должны сохраняться в памяти ЭВМ. Правильная вычислительная схема использует только те коэффициенты матрицы, которые находятся внутри указанной полосы. Уменьшение ширины полосы приводит к сокращению времени вычислений.
Ширина полосы B вычисляется по формуле
где R – максимальная по элементам величина наибольшей разности между номерами узлов в отдельном элементе; Q — число неизвестных (число степеней свободы в каждом узле). Минимизация величины В связана с минимизацией R, что может быть осуществлено последовательной нумерацией узлов при движении в направлении наименьшего размера тела против часовой стрелки. Правильная нумерация узлов экономит машинную память более чем на 60%, хотя не влияет на вычислительные аспекты задачи.
Построение градиентной матрицы.Для плоского КЭ «e» в форме треугольника с вершинами i, j, k с узловыми координатами соответственно ( 
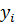
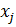
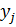
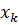
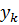
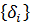
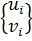
а для трех узлов i, j, k шесть компонент образуют вектор перемещений внутри КЭ «e»:

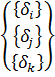
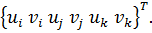
Простейшими интерполяционными функциями являются линейные полиномы
u= 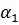
v= 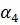
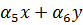
Значения шести постоянных 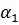
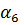
Система уравнений для перемещений u узлов i, j, k:
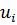
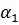
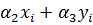
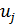
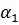
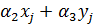
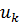
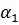
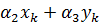
позволяет определить коэффициенты 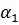
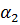
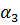
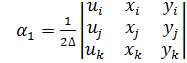
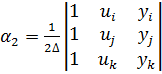
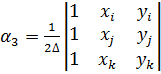
где ∆ — площадь треугольника ijk, удвоенное значение которой равно определителю
2∆=det 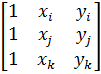
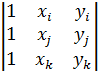
После подстановки 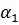
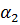
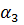
u= 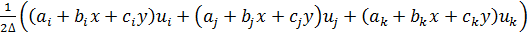
где коэффициенты определяются через координаты узлов КЭ:
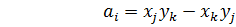
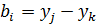
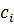
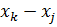
Остальные коэффициенты получаются циклической перестановкой индексов i, j, k.
Аналогично можно представить перемещение v, пользуясь вторым уравнением (10.4):
v= 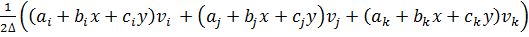
Вектор перемещений внутри КЭ «e»принимает вид
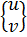
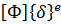

где функции формы 
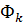

Выбранная функция перемещений автоматически гарантирует неразрывность (совместность) перемещений между смежными КЭ, т.к. вдоль любой стороны треугольника они изменяются линейно; следовательно, из равенства перемещений в узлах следует их равенство по всей границе.
Вектор полной деформации в любой точке КЭ характеризуется тремя составляющими 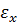
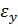
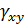
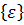
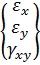
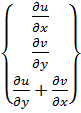
Подставляя (10.10) в (10.11) получим
Матрица 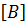
Матрица напряжений.Для упругого изотропного материала физические соотношения т.е. зависимости между напряжениями и деформациями, в данном случае закон Гука, линейны и определяются уравнениями:
где 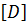
где 𝐸 ‒модуль упругости; 𝜇 ‒ коэффициент Пуассона.
Используя (10.12) и (10.13), напряжения в КЭ 𝑒можно выразить через перемещения его узлов
где матрица 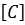
10.2. Матрица жесткости треугольного конечного элемента.МКЭ удобно трактовать как обобщение методов строительной механики стержневых систем на расчет систем континуальных. Тогда он легко распространяется и на комбинированные системы, т.е. системы, содержащие элементы различной мерности. В отличие от стержневых систем, для континуальных систем, в частности, плоской задачи, метод является приближенным.
Матрица жесткости 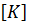
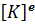
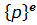
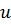
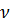
где энергия деформации 𝑈 определяется выражением (в соответствии с формулой Клапейрона):
Энергия деформации 𝑈 для КЭ 𝑒, с учетом матричного представления и полученных ранее соотношений
Напомним, что транспонирование произведения двух матриц выполняется по формуле (лк.1 ЧМ ч.1):
Работа 𝐴, совершаемая приложенными силами, может быть разделена на три части:
‒ работа 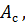
‒работа 
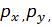
‒работа 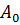
Работу 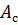
Поверхностные и объемные силы можно также привести к узловым. Тогда
𝐴 = 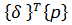

При этом выражение для полной потенциальной энергии для КЭ принимает вид:
Чтобы согласно вариационному принципу Лагранжа минимизировать величину 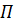
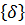
Здесь использованы известные из векторной алгебры формулы дифференцирования произведения матриц по вектору 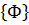
Теперь матрица жесткости элемента 𝑖𝑗𝑘 определяется так:
Отметим единообразие выражений для матриц жесткости стержневых и плоских (10.20) КЭ.
Если толщина 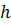
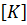
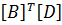
где: Δ ‒ площадь КЭ; 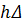
Матрица жесткости является симметричной и имеет блочную структуру:
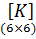
где 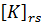
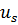

Реактивные усилия в связях, наложенных на узлы 𝑖, 𝑗, 𝑘, вызванные перемещениями 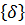
так, например, 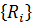
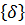
При ОПНС подматрицы имеют второй порядок и определяются следующим образом:
где 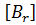
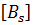
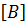
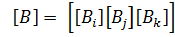
Такая форма записи удобна для компьютерных вычислений.
Узловые силы, связанные с объемными силами X и Y (проекции их интенсивностей на оси x и y), определяются выражениями:
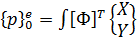

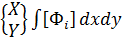
Т.к. функции формы матрицы 
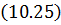
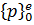
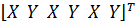
Узловые силы, вызванные поверхностными нагрузками 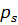
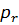
Отметим, что задача о напряженно-деформированном состоянии плоского КЭ решена путем приближенного задания функций формы. Поэтому и метод является приближенным. Увеличить точность решения можно либо путем увеличения числа КЭ, на которое разбивается область Ω, либо путем увеличения числа узловых точек, т.е. числа степеней свободы для каждого из КЭ (последнее путем повышения степени интерполирующего полинома).
10.3. Построение глобальной матрицы жесткости. Поскольку полная потенциальная энергия (функционал) для рассматриваемой области 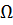
то, минимизируя этот функционал, получим следующую общую систему уравнений:
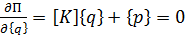
где 
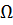
Уравнения (10.28) являются, по сути, уравнениями равновесия. Поскольку координатные функции в методе конечных элементов отличны от нуля только на ограниченной области 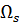
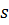
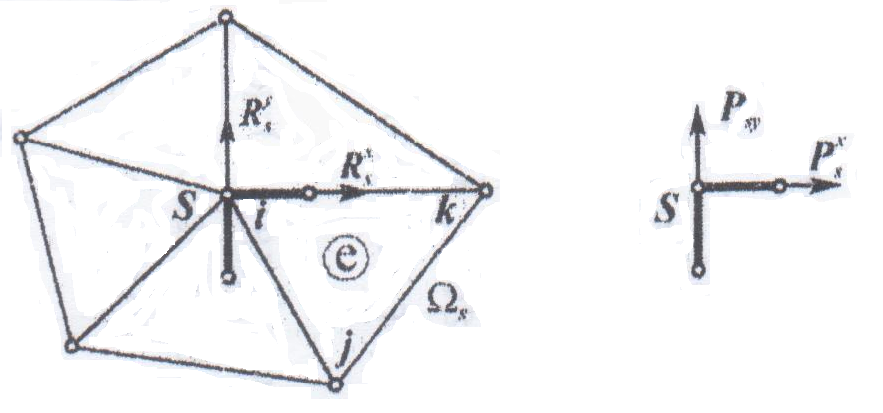
Пусть 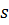
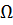
Перемещение любого узла одного из 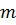
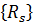
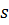
Для показанного на рис. 1 конечного элемента 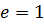
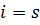
Из условий равновесия узла 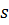
где 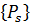
Вектор 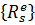
где 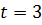
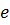
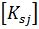
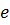
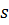

Из подстановки (10.32) в (10.31) следует
где 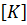
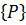
Линейные алгебраические уравнения типа (10.33) составляются для всех узлов расчетной схемы области 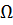

Из матрицы жесткости исключаются те строки и столбцы (а из грузового вектора – элементы), номера которых отвечают узловым связям, наложенный на диск. Обычно, для упрощения индексации, размерность исходной матрицы сохраняют. В случае, если например 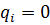
Реакция 
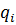
После определения вектора 
http://skysmart.ru/articles/mathematic/reshenie-sistem-uravnenij
http://poisk-ru.ru/s5812t6.html