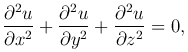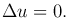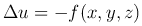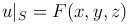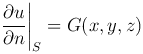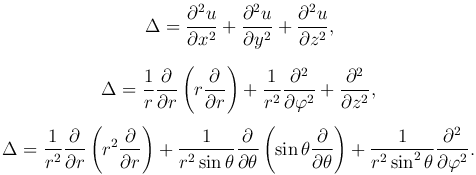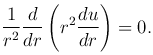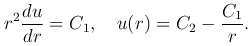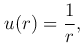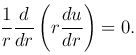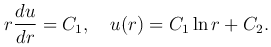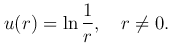Что такое стационарное уравнение лапласа

Уравнение Лапласа

Многие стационарные физические задачи, т.е. такие, в которых рассматриваются явления, неизменные с течением времени (исследования потенциальных течений жидкости, определение формы нагруженной мембраны, задачи теплопроводности и диффузии в стационарных случаях и др.) сводятся к решению уравнения Пуассона вида

(2.88)

Если , то уравнение (2.88) называется уравнением Лапласа. Для простоты будем рассматривать двумерное уравнение Лапласа

(2.89)

Решение этого уравнения будем искать для некоторой ограниченной области Gизменения независимых переменных х, у. Границей области Gявляется замкнутая линия L. Для полной формулировки краевой задачи кроме уравнения Лапласа нужно задать граничное условие на границе L. Примем его в виде

(2.90)

Задача, состоящая в решении уравнения Лапласа (или Пуассона) при заданных значениях искомой функции на границе расчетной области, называется задачей Дирихле.

Одним из способов решения стационарных эллиптических задач, в том числе и краевой задачи (2.89), (2.90), является их сведение к решению некоторой фиктивной нестационарной задачи (гиперболической или параболической), найденное решение которой при достаточно больших значениях времени tблизко к решению исходной задачи. Такой способ решения называется методом установления.

Поскольку решение U(x,y) уравнения (2.89) не зависит от времени, то можно в это уравнение добавить равный нулю (при точном решении) член ¶U/¶t. Тогда уравнение (2.89) примет вид

(2.91)

Это известное нам уравнение теплопроводности, для которого в разд. 2.3.2, 2.3.3 уже строили разностные схемы. Остается только задать начальное условие. Его можно принять практически в произвольном виде, согласованном с граничными условиями. Примем

(2.92)

Граничное условие (2.90) при этом остается стационарным, т. е. не зависящим от времени.

Процесс численного решения уравнения (2.91) с условиями (2.92), (2.90) состоит в переходе при t→∞ от произвольного значения (2.92) к искомому стационарному решению. Счет ведется до выхода решения на стационарный режим. Естественно, решением ограничиваются при некотором достаточно большом t, если искомые значения на двух последовательных слоях совпадают с заданной степенью точности.

Метод установления фактически представляет итерационный процесс решения задачи (2.91) с условиями (2.92), (2.90), причем на каждой итерации значения искомой функции получаются путем численного решения некоторой вспомогательной задачи. В теории разностных схем показано, что этот итерационный процесс сходится к решению исходной задачи, если такое стационарное решение существует.

Другой способ решения задачи Дирихле состоит в построении разностной схемы путем аппроксимации уравнения (2.89). Введем в прямоугольной области Gсетку с помощью координатных прямых х = const и у = const. Примем для простоты значения шагов по переменным х и у равными h(предполагается, что стороны области Gсоизмеримы). Значения функции Uв узлах (xi, yj) заменим значениями сеточной функции uij. Тогда, аппроксимируя в уравнении (2.89) вторые производные с помощью отношений конечных разностей, получим разностное уравнение (шаблон изображен на рис. 2.27).

(2.93)

Рис. 2.27. Шаблон для уравнения Лапласа

С помощью данного уравнения можно записать систему линейных алгебраических уравнений относительно значений сеточной функции в узлах в виде

(2.94)

Значения сеточной функции в узлах, расположенных на границе расчетной области, могут быть найдены из граничного условия (2.90):

В теории разностных схем доказывается, что решение построенной разностной задачи существует, а сама схема устойчива.

Перейдем теперь, к практическому вычислению искомых значений, т.е. к решению системы (2.94). Каждое уравнение системы (за исключением тех, которые соответствуют узлам, расположенным вблизи границ) содержит пять неизвестных. Одним из наиболее распространенных методов решения этой системы линейных уравнений является итерационный метод. Каждое из уравнений записываем в виде, разрешенном относительно значения uij в центральном узле (см. рис. 2.27):

(2.95)

Алгоритм решения задачи Дирихле с использованием итерационного метода Гаусса-Зейделя решения системы разностных уравнений (2.95) изображен на рис. 2.28. В алгоритме предусмотрен выбор начальных значений uij. Иногда полагают, что uij=0 для всех i, j.

Рис. 2.28. Алгоритм решения задачи Дирихле

Итерационный процесс контролируется максимальным отклонением М значений сеточной функции в узлах для двух последовательных итераций. Если его значение достигнет некоторого заданного малого числа ε,итерации прекращаются и происходит вывод результатов.

Рассмотренные разностные схемы метода сеток используют конечно-разностные аппроксимации входящих в уравнения производных по всем переменным. В ряде случаев уравнение с частными производными удобно привести к системе обыкновенных дифференциальных уравнений, в которых оставлены производные искомой функции лишь по одной переменной.

Такой способ можно использовать и для решения уравнения Лапласа (2.89). Пусть требуется решить для него задачу Дирихле в прямоугольнике ABCD(рис. 2.29). Разобьем прямоугольник на полосы с помощью прямых, параллельных оси х. Для определенности проведем три отрезка l1, l2, l3, которые разделят прямоугольник на четыре полосы постоянной ширины h. Решение Uзадачи Дирихле приближенно заменим набором функций ui,каждая из которых определена на отрезке li и зависит только от одной переменной х, т.е.ui= ui(х) (i = 1,2,3). На отрезках l0 и l4 значения u0(x) и u4(x) заданы граничными условиями.

Рис. 2.29. К решению задачи Дирихле в прямоугольнике ABCD

Построим разностную схему для определения значений функций u(х). Аппроксимируя в уравнении (2.89) вторую производную по у с помощью отношения конечных разностей, получаем

(2.96)

Таким образом, решение задачи Дирихле (2.89), (2.90) сводятся к решению краевой задачи для системы обыкновенных дифференциальных уравнений (2.96) относительно значений искомой функции вдоль прямых l1, l2, l3. В этом состоит метод прямых. Граничные условия для уравнений (2.96) при х = а, х = bможно получить из уравнений

Направление дискретизации у обычно легко выбрать в тех случаях, когда заранее известен характер поведения искомой функции, это направление должно соответствовать направлению наибольшей гладкости функции.

Метод прямых широко используют для решения нестационарных задач. Например, если имеются две независимые переменные х, t, а искомый параметр является гладкой функцией переменной х, то дискретизацию вводят по этой переменной. Тогда исходную задачу заменяют задачей Коши для системы обыкновенных дифференциальных уравнений вида:

Применение преобразования Лапласа к решению
линейных дифференциальных уравнений и систем

1°. Общие сведения о преобразовании Лапласа: оригинал и изображение

Функцией-оригиналом называется комплекснозначная функция действительного переменного , удовлетворяющая следующим условиям:

2) функция интегрируема на любом конечном интервале оси ;

3) с возрастанием модуль функции растет не быстрее некоторой показательной функции, т. е. существуют числа 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADoAAAAQBAMAAAC1onFLAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAgUHAYqEh5RGR0VIxELEI83NdAAABBklEQVQY02NgIAAcBRWA5EVBMVRhDjUwdfq/AZCc/kUBVXa6sC2IYjNfwMDANN8AVZKxguExiGYR/sDAwOcvAGK7XIDJsgcw7D8ApFlVfzAwCM0HG8yysAEqe16AQR+kgZ3xEwNbwHqIIMvKBAgDaJY+yLJklt8MfB2foXpYTCHS8gIM+SBZR6aPDFu4P8IsZDI9AJXtB8kGsX3leMD5Ce5aJuMDEFmwyQUMnzkTuD4gZIORZNkMGJYrQkyBmgx2PdDB+hOAzhBgsDdg2C8AleSGuqp9AsP+DQwMXQIMQL/GQ8ORZSnUR5y1DOFA3/7/zyDJsB5IooYG7yvXGoz4aoAzeYQYGADRdjuTYajQpgAAAABJRU5ErkJggg==» /> и такие, что для всех имеем

Изображением функции-оригинала по Лапласу называется функция комплексного переменного , определяемая равенством

при s_0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAFIAAAATBAMAAADxBkdhAAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADXRSTlMAQcCBEFor0KCR6LBxSK9m8wAAAVlJREFUKM9jYCAaJBsbGx8jSqVj71LRWVuIUiqrwMB6iViVDHcT0AQNcaoUQBN0LsVh+3UGBlYlVSAnqUVaFarUASrPuKkFprJQ8JQKA0NUQmwAA0vBpZZciPnOxVClUQmzYSoXW1xyYGC7ycBewMB65DYD7waIOCtUaTHDDQY2EajtQMR8WVD6AgNj6lUGXgWoEawVYKWrpiYw9AglQFSyX2PgvGFsbMDAwHmFQXYDTKUGWOXZuwVsC1gVICqZ7jAw3wHLAl1gGwBVWAkOOja38IvMCowXoCpvMrDdYGAAKvGdwLAKotAV6szYCYzXgCovglQWMHBcZ1OYlcDWABRX4FmG6vVTCcwKTGCVsnfvKrDUWgQwX9oElJvb0ZSAGvJOmzUcOCFmgkP3IBCDDClngxjVipSEGBig7kQGLDexJg2g3zegCfFcxZ6KZoSjJ6FJShOwGwqMIwCRZlRL/vuSSQAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />. Условие 3 обеспечивает существование интеграла (2).

Преобразование (2), ставящее в соответствие оригиналу его изображение , называется преобразованием Лапласа. При этом пишут .

Свойства преобразования Лапласа

Всюду в дальнейшем считаем, что

I. Свойство линейности. Для любых комплексных постоянных и

II. Теорема подобия. Для любого постоянного 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADEAAAAQBAMAAABNQoq8AAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcGe2BFbQSGBMfCxcU2qjNsAAADDSURBVBjTY2AgDYgvxCHB5WyyALtM9wW2HUhcDgs4006A8TGyyprjAlCWiwCjCpDNekkzACLQrA6RYnwkwKgHZK42DVFghkq5CcBlAhi4NjOwPSuGGtMJlmJ/xMCgV8DA9JSB6yXc8kg3IMEKkelTAOo2gMv4Iuypm8DA+DoArgVkGiPQbdpgGdY3DDAXQP3DAPKPiAFjkRMbiqsZ1iWwPweGkY+RafYxEL8IJsHA5jklAeSShQysIHtYEaHD2JbKwAAA/gYrl5lLD9QAAAAASUVORK5CYII=» />

III. Дифференцирование оригинала. Если есть оригинал, то

Обобщение: если раз непрерывно дифференцируема на и если есть оригинал, то

IV. Дифференцирование изображения равносильно умножению оригинала на «минус аргумент», т.е.

V. Интегрирование оригинала сводится к делению изображения на

VI. Интегрирование изображения равносильно делению на оригинала:

(предполагаем, что интеграл сходится).

VII. Теорема запаздывания. Для любого положительного числа

VIII. Теорема смещения (умножение оригинала на показательную функцию). Для любого комплексного числа

IX. Теорема умножения (Э. Борель). Произведение двух изображений и также является изображением, причем

Интеграл в правой части (14) называется сверткой функций и и обозначается символом

Теорема XI утверждает, что умножение изображений равносильно свертыванию оригиналов , т.е.

Отыскание оригиналов дробно-рациональных изображений

Для нахождения оригинала по известному изображению , где есть правильная рациональная дробь, применяют следующие приемы.

1) Эту дробь разлагают на сумму простейших дробей и находят для каждой из них оригинал, пользуясь свойствами I–IX преобразования Лапласа.

2) Находят полюсы этой дроби и их кратности . Тогда оригиналом для будет функция

где сумма берется по всем полюсам функции .

В случае, если все полюсы функции простые, т.е. , последняя формула упрощается и принимает вид

Пример 1. Найти оригинал функции , если

Решение. Первый способ. Представим в виде суммы простейших дробей

и найдем неопределенные коэффициенты . Имеем

Полагая в последнем равенстве последовательно , получаем

Находя оригиналы для каждой из простейших дробей и пользуясь свойствам линейности, получаем

Второй способ. Найдем полюсы функции . Они совпадают с нулями знаменателя . Таким образом, изображение имеет четыре простых полюса . Пользуясь формулой (17), получаем оригинал

Пример 2. Найти оригинал , если .

Решение. Данная дробь имеет полюс кратности и полюс кратности . Пользуясь формулой (16), получаем оригинал

2°. Решение задачи Коши для линейных дифференциальных уравнений с постоянными коэффициентами

Пусть требуется найти решение дифференциального уравнения второго порядка с постоянными коэффициентами

Будем считать, что функция и решение вместе с его производньь ми до второго порядка включительно являются функциями-оригиналами. Пусть . По правилу дифференцирования оригиналов с учетом (2) имеем

Применяя к обеим частям (1) преобразование Лапласа и пользуясь свойством линейности преобразования, получаем операторное уравнение

Решая уравнение (20), найдем операторное решение

Находя оригинал для , получаем решение уравнения (18), удовлетворяющее начальным условиям (19).

Аналогично можно решить любое уравнение n-го порядка с постоянными коэффициентами и с начальными условиями при .

Пример 3. Решить дифференциальное уравнение операторным методом

Решение. Пусть , тогда по правилу дифференцирования оригинала имеем

Известно, что поэтому, переходя отданной задачи (21)–(22) к операторному уравнению, будем иметь

Легко видеть, что функция удовлетворяет данному уравнению и начальному условию задачи.

Пример 4. Решить уравнение .

Решение. Так как и по условию , то операторное уравнение будет иметь вид

Отсюда находим операторное решение

Разлагаем правую часть на элементарные дроби:

Переходя к оригиналам, получаем искомое решение .

Пример 5. Решить уравнение .

Решение. Так как и по условию , то операторное уравнение будет иметь вид

и, следовательно, операторное решение

Разложим правую часть на элементарные дроби:

Переходя к оригиналам, получим решение поставленной задачи

3°. Решение систем линейных дифференциальных уравнений с постоянными коэффициентами

Пусть требуется найти решение системы двух уравнений с постоянными коэффициентами

удовлетворяющее начальным условиям

Будем предполагать, что функции , а также и являются функциями-оригиналами.

По правилу дифференцирования оригиналов с учетом (24) имеем

Применяя к обеим частям каждого из уравнений системы (23) преобразование Лапласа, получим операторную систему

Эта система является линейной алгебраической системой двух уравнений с двумя неизвестными и . Решая ее, мы найдем и , а затем, переходя к оригиналам, получим решение системы (23), удовлетворяющее начальным условиям (24). Аналогично решаются линейные системы вида

Пример 6. Найти решение системы дифференциальных уравнений операторным методом

удовлетворяющее начальному условию .

Решение. Так как и , то операторная система будет иметь вид

Решая систему, получаем

Разлагаем дроби, стоящие в правых частях, на элементарные:

Переходя к оригиналам, получим искомое решение

Уравнение Лапласа

Рассмотрим уравнение с частными производными вида

где u=u(x, y, z). Это уравнение называется уравнением Лапласа.

Левая часть обозначается Δu и называется оператором Лапласа. Таким образом, это уравнение преобразуется к виду:

Данному уравнению удовлетворяет потенциал скорости безвихревого течения несжимаемой (с постоянной плотностью) жидкости; потенциал сил тяготения или сил взаимодействия электрических зарядов во всех точках пространства, находящихся вне притягивающих масс или вне зарядов, создающих поле; температура в однородном теле, если теплообмен является стационарным, т.е. температура u зависит только от места, но не от времени и др.

называется уравнением Пуассона.

Уравнение Лапласа и уравнение Пуассона является уравнениями эллиптического типа.

Определение. Функцию, непрерывную в некоторой области вместе со своими частными производными до второго порядка включительно и удовлетворяющую уравнению Лапласа, называют гармонической.

Обычно в задачах, связанных с уравнением Лапласа или Пуассона, искомое решение должно удовлетворять уравнению в области D, а также некоторому дополнительному условию на границе S области D.

Если надо определить функцию, гармоническую в области D, когда на границе S области D заданы ее значения, т.е.

(первая краевая задача), то такая задача называется задачей Дирихле.

Если же надо определить функцию, гармоническую в области D, когда на границе S задается значение нормальной производной

(вторая краевая задача), то такая задача называется задачей Неймана.

Определение. Если решение задачи ищут в области D, внутренней (внешней) по отношению к поверхности S, то соответствующую задачу называют внутренней (внешней) краевой задачей.

Фундаментальные решения уравнения Лапласа

Рассмотрим уравнение Лапласа

где оператор Лапласа в декартовой, цилиндрической и сферической системах координат определяется соответственно

Важную роль при решении задач для уравненийй Лапласа и Пуассона представляют решения, обладающие сферической или цилиндрической симметрией.

Найдем решение уравнения Лапласа, удовлетворяющее условию сферической симметрии, когда функция u зависит только от расстояния 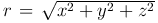точки M(x, y, z) до начала координат. В этом случае уравнение Лапласа в сферической системе координат имеет вид

Интегрируя это уравнение, получим

которая удовлетворяет уравнению Лапласа всюду, кроме точки r=0, где она обращается в бесконечность. Такую функцию называют фундаментальным решением уравнения Лапласа в пространстве.

В задаче с осевой симметрией, когда функция u в цилиндрической системы координат не зависит от φ и z, уравнение Лапласа имеет вид

Интегрируя это уравнение, получим

Эта функция называется фундаментальным решением уравнения Лапласа на плоскости.