Движение тела с переменной массой. Уравнение Мещерского. Формула Циолковского
Вы будете перенаправлены на Автор24
Уравнение движения тела с переменной массой
Под переменной массой будем понимать массу тел, которая при медленном движении тел меняется за счет потери или приобретения вещества.
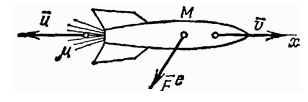
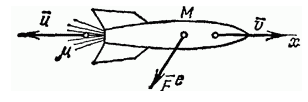
Выведем уравнение движения материальной точки с переменной массой на примере движения ракеты. Принцип действия ракеты очень прост. Ракета с большой скоростью выбрасывает вещество (газы), воздействуя на него с большой силой. Выбрасываемое вещество с той же, но противоположно направленной силой в свою очередь действует на ракету и сообщает ей ускорение в противоположном направлении. На ракету действуют внешние силы: сила земной тяжести, гравитационное притяжение Солнца и планет, а также сила сопротивления среды, в которой движется ракета.
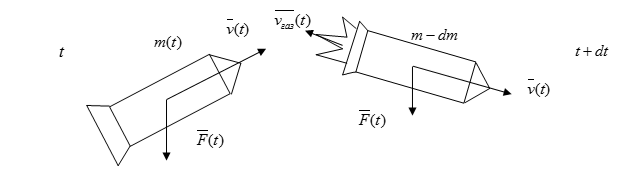
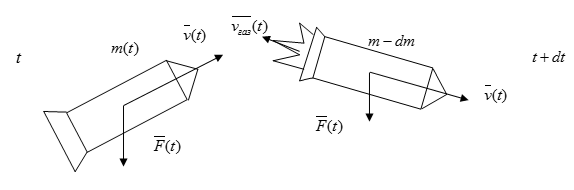
Пусть $m(t)$- масса ракеты в произвольный момент времени $t$, а $v(t)$- ее скорость в тот же момент. Количество движения ракеты в этот момент времени будет $mv$. Спустя время $dt$ масса и скорость ракеты получат приращение $dm$ и $dv$ (величина $dm$ отрицательна). Количество движения ракеты станет равным $(m+dm)(v+dv)$. Сюда надо добавить количество движения газов, образовавшихся за время $dt$. Оно равно $dm_ <газ>v_ <газ>$, где $dm_ <газ>$- масса газов, образовавшихся за время $dt$, а $v_ <газ>$- их скорость. Вычитая из суммарного количества движения в момент $t+dt$ количество движения системы в момент времени $t$, найдем приращение этой величины за время $dt$. Это приращение равно $Fdt$, где $F$- геометрическая сумма всех внешних сил, действующих на ракету. Таким образом:
Время $dt$ и приращения $dm$ и $dv$ устремим к нулю, т.к. нас интересуют предельные отношения или производные $dm/dt$ и $dv/dt$. Поэтому, раскрывая скобки, можно отбросить произведение $dm\cdot dv$, как бесконечно малую высшего порядка. Далее, ввиду сохранения массы, $dm+dm_ <газ>=0$. Пользуясь этим, можно исключить массу газов $dm_ <газ>$. А разность $v_ <отн>=v_ <газ>-v$ есть скорость истечения газов относительно ракеты — скорость газовой струи. С учетом этих замечаний уравнение (1) преобразуется к виду:
Готовые работы на аналогичную тему
Разделив на $dt$, получаем:
Уравнение Мещерского
По форме уравнение (3) совпадает с уравнением, выражающим второй закон Ньютона. Однако масса тела $m$здесь не постоянна, а меняется во времени из-за потери вещества. К внешней силе $F$ добавляется дополнительный член $v_ <отн>\frac
Формула Циолковского
Применим уравнение (2) к движению ракеты, на которую не действуют никакие внешние силы. Полагая $F=0$, получим:
Допустим, что ракета движется прямолинейно в направлении, противоположном скорости газовой струи $v_ <отн>$. Если направление полета принять за положительное, то проекция вектора $v_ <отн>$ на это направление будет отрицательной и равной $-v_ <отн>$. Поэтому в скалярной форме предыдущее уравнение можно записать так $mdv=v_ <отн>dm$. Тогда:
Скорость газовой струи $v_ <отн>$ может меняться во время полета. Однако простейшим и наиболее важным является случай, когда она постоянна. Предположение о постоянстве сильно облегчает решение уравнения (4). В этом случае:
Значение постоянной интегрирования С определяется начальными условиями. Допустим, что в начальный момент времени скорость ракеты равна нулю, а ее масса равна $m_ <0>$. Тогда из предыдущего уравнения получаем:
Последнее соотношение называется формулой Циолковского.
Формула Циолковского позволяет рассчитать запас топлива, необходимый, чтобы сообщить ракете скорость $\upsilon $.
Величина достигаемой ракетой максимальной скорости не зависит от времени сгорания топлива.
Оптимальным путем изменения достигаемой максимальной скорости является увеличение относительной скорости истечения газов.
Для получения первой космической скорости при меньшем соотношении между массой ракеты и требуемой массы топлива целесообразно использование многоступенчатых ракет.
Примеры
Космический корабль двигался с постоянной по величине скоростью $v$. Для изменения направления его полета включается двигатель, выбрасывающий струю газа со скоростью $v_ <отн>$ относительно корабля в направлении, перпендикулярном к его траектории. Определить угол $\alpha $, на который повернется вектор скорости корабля, если начальная масса его $m_ <0>$, а конечная $m$.
Решение:
Ускорение корабля по абсолютной величине равно:
$a=\omega ^ <2>r=\omega v$, причем $v=const$. Поэтому уравнение движения:
$m\frac
Так как $d\alpha =\omega dt$ есть угол поворота за время $dt$, интегрируя наше уравнение, получим:
Ответ: угол поворота вектора скорости равен: $\alpha =\frac
Ракета перед стартом имеет массу $m_ <0>=250$кг. На какой высоте окажется ракета через $t=20$с после начала работы двигателей? Расход топлива равен $\mu =4$кг/с и скорость истечения газов относительно ракеты $v_ <отн>$$=1500$м/с постоянны. Поле тяготения Земли считать однородным.
Дано: $m_ <0>=250$кг, $t=20$с, $\mu =4$кг/с, $v_<отн>=1500$м/с.
Решение:
Запишем уравнение Мещерского в однородном поле тяготения Земли в виде:
где $m=m_ <0>-\mu t$, а $v_ <0>$- скорость ракеты в момент времени $t$. Разделяя переменные получаем:
Решение данного уравнения, удовлетворяющего начальному условию $v_ <0>=0$ при $t=0$, имеет вид:
Учитывая что $H_ <0>=0$ при $t=0$ получим:
Подставляя начальные значения, получаем:
Ответ: через $20$с ракета окажется на высоте $H=3177,5$м.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 06 04 2021
Движение тела с переменной массой
Для начала сформулируем, что такое переменная масса.
Переменная масса – это масса тела, которая может меняться при медленных движениях из-за частичных приобретений или потерь составляющего вещества.
Уравнение движения материальной точки с переменной массой
Чтобы записать уравнение движения для тела с такой массой, возьмем для примера движение ракеты. В основе ее перемещений лежит очень простой принцип: она движется за счет выброса вещества с большой скоростью, а также сильного воздействия, оказываемого на это вещество. В свою очередь выбрасываемые газы также оказывают воздействие на ракету, придавая ей ускорение в противоположном направлении. Кроме того, ракета находится под действием внешних сил, таких, как гравитация Солнца и других планет, земная тяжесть, сопротивление среды, в которой она совершает движение.
Обозначим массу ракеты в какой-либо момент времени t как m ( t ) , а ее скорость как v ( t ) . То количество движения, которая она при этом совершает, будет равно m v . После того, как пройдет время d t , обе эти величины получат приращение (соответственно d m и d v , причем значение d m будет меньше 0 ). Тогда количество движения, совершаемого ракетой, станет равно:
( m + d m ) ( v + d v ) .
Нам необходимо учитывать тот момент, что за время d t также происходит движение газов. Это количество тоже нужно добавить в формулу. Оно будет равно d m г а з v г а з . Первый показатель означает массу газов, которые образуются за указанное время, а второй – их скорость.
Теперь нам нужно найти разность между суммарным количеством движения за время t + d t и количеством движения системы во время t . Так мы найдем приращение данной величины за время d t , которое будет равно F d t (буквой F обозначена геометрическая сумма всех тех внешних сил, которые действуют в это время на ракету).
В итоге мы можем записать следующее:
( m + d m ) ( v + d v ) + d m г а з + v г а з — m v = F d t .
Поскольку нам важны именно предельные значения d m d t , d v d t и их производные, приравняем эти показатели к нулю. Значит, после раскрытия скобок произведение d m · d v может быть отброшено. С учетом сохранения массы получим:
d m + d m г а з = 0 .
Теперь исключим массу газов d m г а з и получим скорость, с которой газы будут покидать ракету (скорость струи вещества), выражающаяся разностью v о т н = v г а з — v . Учитывая эти преобразования, можно переписать исходное уравнение в следующем виде:
d m v = v о т н d m + F d t .
Теперь разделим его на d t и получим:
m d v d t = v о т н d m d t + F .
Уравнение Мещерского
Форма полученного уравнения точно такая же, как у уравнения, выражающего второй закон Ньютона. Но, если там мы имеем дело с постоянной массой тела, то здесь из-за потери вещества она постепенно меняется. К тому же помимо внешней силы нужно учитывать так называемую реактивную силу. В примере с ракетой это будет сила выходящей из нее газовой струи.
Уравнение m d v d t = v о т н d m d t + F впервые вывел русский механик И.В. Мещерский, поэтому оно получило его имя. Также его называют уравнением движения тела с переменной массой.
Формула Циолковского
Попробуем исключить из уравнения движения ракеты внешние силы, воздействующие на нее. Предположим, что движение ракеты прямолинейно, а направление противоположно скорости газовой струи v о т н . Будем считать направление полета положительным, тогда проекция вектора v о т н является отрицательной. Она будет равна — v о т н . Переведем предыдущее уравнение в скалярную форму:
m d v = v о т н d m .
Тогда равенство примет вид:
d v d m = — v о т н m .
Газовая струя может выходить во время полета с переменной скоростью. Проще всего, разумеется, принять ее в качестве константы. Такой случай наиболее важен для нас, поскольку так уравнение решить намного проще.
Исходя из начальных условий, определим, какое значение приобретет постоянная интегрирования С. Допустим, что в начале пути скорость ракеты будет равна 0 , а масса m 0 . Следовательно, из предыдущего уравнения можем вывести:
C = v о т н ln m 0 m .
Тогда мы получим соотношения следующего вида:
v = v о т н ln m 0 m или m 0 m = e v v о т н .
Это соотношение и является формулой Циолковского.
Она предназначена для расчета запаса топлива, с помощью которого ракета может набрать необходимую скорость. При этом время сгорания топлива не обусловливает величину максимальной скорости ракеты. Чтобы разогнаться до предела, нужно увеличить скорость истечения газов. Для достижения первой космической скорости следует изменить конструкцию ракеты. Она должна быть многоступенчатой, поскольку необходимо меньшее соотношение между требуемой массой топлива и массой ракеты.
Разберем несколько примеров применения данных построений на практике.
Условие: у нас есть космический корабль, скорость которого постоянна. Для изменения направления полета в ней нужно включить двигатель, который выбрасывает газовую струю со скоростью v о т н . Направление выброса перпендикулярно траектории корабля. Определите угол изменения вектора скорости при начальной массе корабля m 0 и конечной m .
Решение
Ускорение по абсолютной величине будет равно a = ω 2 r = ω v , причем v = c o n s t .
Значит, уравнение движения будет выглядеть так:
m d v d t = v о т н d m d t перейдет в m v ω d t = — v о т н d m .
Поскольку d a = ω d t является углом поворота за время d t , то после интеграции первоначального уравнения получим:
a = v о т н v ln m 0 m .
Ответ: искомый угол будет равен a = v о т н v ln m 0 m .
Условие: масса ракеты перед стартом равна 250 к г . Вычислите высоту, которую она наберет через 20 секунд после начала работы двигателя. Известно, что топливо расходуется со скоростью 4 к г / с , а скорость истечения газов постоянна и равна 1500 м / с . Поле тяготения Земли можно считать однородным.
Решение
Начнем с записи уравнения Мещерского. Оно будет иметь следующий вид:
m ∆ v 0 ∆ t = μ v о т н — m g .
Здесь m = m 0 — μ t и v 0 – скорость ракеты в заданный момент времени. Разделим переменные:
∆ v 0 = μ v о т н m 0 — μ t — g ∆ t .
Теперь решим полученное уравнение с учетом первоначальных условий:
v 0 = v о т н ln m 0 m 0 — μ t — g t .
С учетом того, что H 0 = 0 при t = 0 , у нас получится:
H = v о т н t — g t 2 2 + v о т н m 0 μ 1 — μ t m 0 ln 1 — μ t m 0 .
Добавим заданные значения и найдем ответ:
H = v о т н t — g t 2 2 + v о т н m 0 μ 1 — μ t m 0 ln 1 — μ t m 0 = 3177 , 5 м .
Ответ: через 20 секунд высота ракеты будет составлять 3177 , 5 м .
Лекция 8. Движение тела переменной массы. Содержание. 1. Уравнение Мещерского 2. Движение ракет. Формула Циолковского РЕПОЗИТОРИЙ БГПУ
- Юлия Белинская 4 лет назад Просмотров:
1 Лекция 8 Движение тела переменной массы Содержание 1 Уравнение Мещерского 2 Движение ракет Формула Циолковского
2 В природе и технике нередки случаи, когда масса тел изменяется с течением времени за счет потери или приобретения вещества Так, масса: метеорита при полете в атмосфере уменьшается в результате отрыва или сгорания его частиц; дождевой капли растет при падении в перенасыщенном водяным паром воздухе; дрейфующей льдины увеличивается при намерзании и уменьшается при таянии; машины для поливки улиц уменьшается при вытекании водяных струй; ракеты уменьшается в результате вытекания газов, которые образуются при сгорании топлива, и т д Во всех этих случаях имеют дело с движением тел переменной массы Уравнения движения тел переменной массы являются следствием законов Ньютона, тем не менее, эти уравнения представляют самостоятельный интерес, главным образом как теоретическая основа ракетной техники
3 Вывод уравнения движения тела переменной массы рассмотрим на примере движения простейшей ракеты Будем рассматривать ракету как достаточно малое тело, положение центра масс которого не изменяется по мере сгорания топлива В этом случае ее можно считать материальной точкой переменной массы, положение которой совпадает с центром масс Будем считать, что вылетающая из ракеты частица газа массой dm взаимодействует с ней только в момент отделения Примем также, что изменение массы ракеты происходит непрерывно, без скачков, т е существует производная массы по времени dm / dt, которая характеризует скорость изменения массы
4 Пусть в момент времени t ракета с топливом имеет массу m, скорость относительно неподвижной системы отсчета (Земли) υ и импульс p = m υ За время dt от ракеты отделяется некоторая масса dm газа, скорость которой относительно ракеты u Относительно выбранной неподвижной системы отсчета ее скорость будет u +υ, а импульс dp ( = dm u + υ ) Масса ракеты станет m-dm, скорость υ + dυ, а импульс p ( )( ) p = m dm υ + dυ В общем случае на ракету будут действовать внешние силы, в числе которых силы гравитационного притяжения Земли, Солнца и планет, а также сила сопротивления среды, в которой она движется
5 В соответствии с основным законом динамики изменение импульса системы (ракета выбрасываемые газы) равно импульсу результирующей внешних сил ( dp = Fdt) или m dm υ + dυ + dm u + υ mυ = Fdt dmdυ md + dmu = Fdt υ ( )( ) ( ) Раскрыв скобки и, пренебрегая произведением как бесконечно малой величиной высшего порядка, получим: Разделив последнее соотношение на dt, получим уравнение dυ dm m = F u dt Это уравнение динамики тела переменной массы впервые было получено профессором Петербургского политехнического института Мещерским и носит его имя dt
6 dυ dm m = F u dt dt Сравнивая полученное уравнение со вторым законом Ньютона, отметим, что левая часть представляет собой произведение массы и ускорения ракеты Следовательно, справа должна стоять сумма сил, которые действуют на ракету Отсюда приходим к выводу, что второе слагаемое в правой части также выражает силу Для выяснения ее природы рассмотрим случай, когда внешние силы отсутствуют ( F = 0 ), т е система ракета выбрасываемые газы является замкнутой На основе закона сохранения импульса можно утверждать, что суммарный импульс системы остается неизменным В этом случае получаем соотношение, на основе которого можно сделать вывод о том, что ракета получает такое же приращение импульса, как и выбрасываемые газы, только в противоположном направлении md υ = dmu
7 Причиной изменения импульсов отдельных частей замкнутой системы могут быть только внутренние силы, действующие между ними Таким образом, на ракету со стороны газов действует сила dm = u dt р Эта сила называется реактивной Она прямо пропорциональна скорости изменения массы тела dm/dt и относительной скорости u отделяемых частиц и направлена в сторону, противоположную вектору u Величину µ = dm / dt называют расходом газа или жидкости Использование реактивной силы лежит в основе работы реактивных двигателей, которые делятся на два основных класса: ракетные и воздушно-реактивные Единственным двигателем, который обеспечивает управляемое движение аппарата в космическом пространстве, является ракетный Значительную часть массы ракеты занимают горючее и окислитель F
8 Реактивная сила возникает в результате вытекания продуктов сгорания через отверстие (сопло), которое сужается для увеличения скорости вытекания В ракетах используется как жидкое, так и твердое топливо, содержащее в себе горючее и окислитель Воздушно-реактивные двигатели работают по принципу одновременного присоединения и отделения частиц Двигатели этого типа делятся на турбореактивные и прямоточные В носовой части турбореактивного двигателя расположен компрессор, засасывающий и сжимающий воздух, который затем поступает в камеру сгорания и служит окислителем для жидкого горючего, подаваемого с помощью форсунок
9 Продукты сгорания, проходя через сопло, вращают турбину, которая приводит в действие компрессор Прямоточный двигатель не имеет компрессора и газовой турбины Воздух засасывается исключительно благодаря движению самолета Этот двигатель, в отличие от турбореактивного, не создает тяги, когда самолет неподвижный, и может использоваться на сверхзвуковых самолетах в сочетании с двигателями других типов Применим уравнение Мещерского к частному случаю движения ракеты, когда на нее не действуют внешние силы Движение ракеты происходит под действием только реактивной силы Направим ось X по оси ракеты, совместив ее с направлением полета В проекции на эту ось уравнение Мещерского примет вид: dυ m = u dt dm dt
10 Разделив на m и сокращая dt, получим: d υ = udm / m Для нахождения скорости ракеты через время t после начала движения проинтегрируем это выражение, учитывая, что за время t скорость увеличивается от 0 до, а масса уменьшается от m 0 до m: υ 0 d υ = u Отсюда получаем формулу для расчета конечной скорости ракеты, где m 0 начальная масса ракеты вместе с топливом; m конечная масса ракеты m m 0 dm m 0 = u ln m m 0 υ
11 υ u ln m 0 = m Эта формула была получена в 1903 г КЭ Циолковским и носит его имя Из нее следует, что конечная скорость, приобретаемая ракетой при отсутствии внешних сил, не зависит от закона изменения массы и ограничена только отношением начальной и конечной масс ракеты Полученная формула позволяет оценить максимальную скорость, которую может развить ракета, если предположить, что внешние силы не действуют Предельная относительная скорость u мax истечения газов через сопло определяется химическим составом и температурой сгорания топлива и обычно не превосходит 3 4 км/с Максимальное значение отношения масс m 0 / m ограничено прочностью конструкции, и для современных материалов ее можно принять 10 Тогда предельная скорость простейшей одноступенчатой ракеты не превысит 7 км/с, что меньше первой космической
12 Для получения космических скоростей Циолковский предложил использовать многоступенчатые ракеты, которые представляют собой несколько «посаженных» друг на друга ракет Когда горючее первой ракеты (ступени) полностью использовано, она отделяется и начинают работать двигатели второй ступени и т д Для запуска космических кораблей и искусственных спутников применяются трехступенчатые ракеты В настоящее время ведутся интенсивные работы по созданию новых типов ракетных двигателей, которые принципиально отличаются от твердотельных и жидкостных реактивных двигателей В атомных двигателях рабочее вещество нагревается в ядерном реакторе и затем вытекает через сопло В ионном ракетном двигателе реактивная сила тяги создается в результате выбрасывания из двигателя заряженных частиц ионов, которые предварительно разгоняются в электрическом поле до больших скоростей
13 Воображение более важно, чем знание АЭйнштейн
http://zaochnik.com/spravochnik/fizika/osnovy-dinamiki/dvizhenie-tela-s-peremennoj-massoj/
http://docplayer.com/61639126-Lekciya-8-dvizhenie-tela-peremennoy-massy-soderzhanie-1-uravnenie-meshcherskogo-2-dvizhenie-raket-formula-ciolkovskogo-repozitoriy-bgpu.html