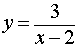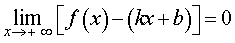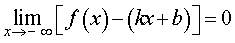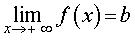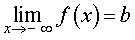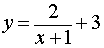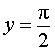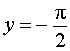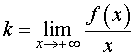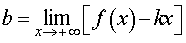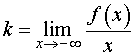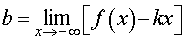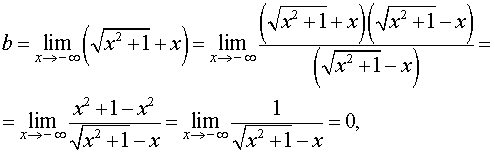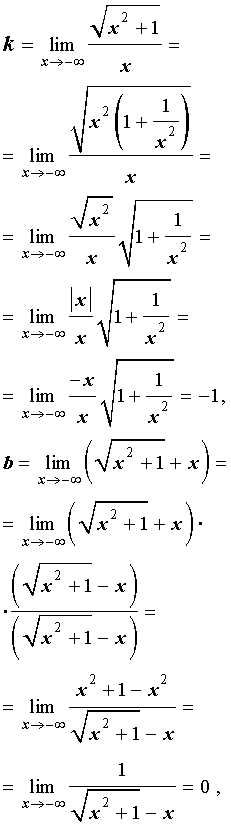Асимптоты графика функций: их виды, примеры решений
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Понятие асимптоты
Если предварительно построить асимптоты кривой, то многих случаях построение графика функции облегчается.
Судьба асимптоты полна трагизма. Представьте себе, каково это: всю жизнь двигаться по прямой к заветной цели, подойти к ней максимально близко, но так и не достигнуть её. Например, стремиться соединить свой жизненный путь с путём желанного человека, в какой-то момент приблизиться к нему почти вплотную, но даже не коснуться его. Или стремиться заработать миллиард, но до достижения этой цели и записи в книгу рекордов Гиннеса для своего случая не достаёт сотых долей цента. И тому подобное. Так и с асимптотой: она постоянно стремится достигнуть кривой графика функции, приближается к нему на минимальное возможное расстояние, но так и не касается его.
Определение 1. Асимптотами называются такие прямые, к которым сколь угодно близко приближается график функции, когда переменная стремится к плюс бесконечности или к минус бесконечности.
Определение 2. Прямая называется асимптотой графика функции, если расстояние от переменной точки М графика функции до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат по какой-либо ветви графика функции.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Вертикальные асимптоты
Первое, что нужно узнать о вертикальных асимптотах: они параллельны оси Oy .
Определение. Прямая x = a является вертикальной асимптотой графика функции, если точка x = a является точкой разрыва второго рода для этой функции.
Из определения следует, что прямая x = a является вертикальной асимптотой графика функции f(x) , если выполняется хотя бы одно из условий:
(предел функции при значении аргумента, стремящимся к некоторому значению a слева, равен плюс или минус бесконечности)
(предел функции при значении аргумента, стремящимся к некоторому значению a справа, равен плюс или минус бесконечности).
- символом
обозначается стремление x к a справа, причём x остаётся больше a;
- символом
обозначается стремление x к a слева, причём x остаётся меньше a.
Из сказанного следует, что вертикальные асимптоты графика функции можно искать не только в точках разрыва, но и на границах области определения. График функции, непрерывной на всей числовой прямой, вертикальных асимптот не имеет.
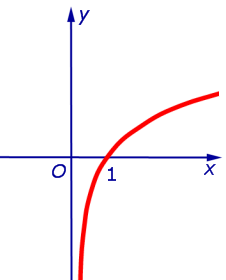
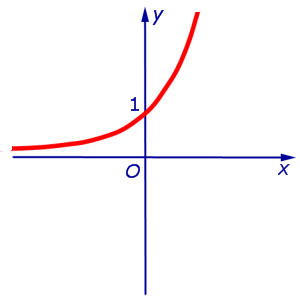
Пример 1. График функции y=lnx имеет вертикальную асимптоту x = 0 (т.е. совпадающую с осью Oy ) на границе области определения, так как предел функции при стремлении икса к нулю справа равен минус бесконечности:
Найти асимптоты графика функции самостоятельно, а затем посмотреть решения
Пример 2. Найти асимптоты графика функции 
Пример 3. Найти асимптоты графика функции
Пример 4. Найти асимптоты график функции 
Горизонтальные асимптоты
Первое, что нужно узнать о горизонтальных асимптотах: они параллельны оси Ox .
Если 
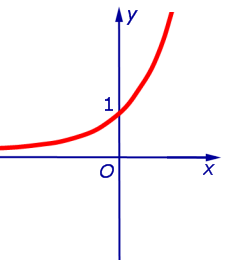
Пример 5. График функции
при a > 1 имеет левую горизонтальную асимпототу y = 0 (т.е. совпадающую с осью Ox ), так как предел функции при стремлении «икса» к минус бесконечности равен нулю:
Правой горизонтальной асимптоты у кривой нет, поскольку предел функции при стремлении «икса» к плюс бесконечности равен бесконечности:
Наклонные асимптоты
Вертикальные и горизонтальные асимптоты, которые мы рассмотрели выше, параллельны осям координат, поэтому для их построения нам требовалось лишь определённое число — точка на оси абсцисс или ординат, через которую проходит асимптота. Для наклонной асимптоты необходимо больше — угловой коэффициент k, который показывает угол наклона прямой, и свободный член b, который показывает, насколько прямая находится выше или ниже начала координат. Не успевшие забыть аналитическую геометрию, а из неё — уравнения прямой, заметят, что для наклонной асимптоты находят уравнение прямой с угловым коэффициентом. Существование наклонной асимптоты определяется следующей теоремой, на основании которой и находят названные только что коэффициенты.
Теорема. Для того, чтобы кривая y = f(x) имела асимптоту y = kx + b , необходимо и достаточно, чтобы существовали конечные пределы k и b рассматриваемой функции при стремлении переменной x к плюс бесконечности и минус бесконечности:


Найденные таким образом числа k и b и являются коэффициентами наклонной асимптоты.
В первом случае (при стремлении икса к плюс бесконечности) получается правая наклонная асимптота, во втором (при стремлении икса к минус бесконечности) – левая. Правая наклонная асимптота изображена на рис. снизу.
При нахождении уравнения наклонной асимптоты необходимо учитывать стремление икса и к плюс бесконечности, и к минус бесконечности. У некоторых функций, например, у дробно-рациональных, эти пределы совпадают, однако у многих функций эти пределы различны а также может существовать только один из них.
При совпадении пределов при иксе, стремящемся к плюс бесконечности и к минус бесконечности прямая y = kx + b является двусторонней асимптотой кривой.
Если хотя бы один из пределов, определяющих асимптоту y = kx + b , не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).
Нетрудно видеть, что горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0 .
Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.
Пример 6. Найти асимптоты графика функции
Решение. Функция определена на всей числовой прямой, кроме x = 0 , т.е.
Поэтому в точке разрыва x = 0 кривая может иметь вертикальную асимптоту. Действительно, предел функции при стремлении икса к нулю слева равен плюс бесконечности:
Следовательно, x = 0 – вертикальная асимптота графика данной функции.
Горизонтальной асимптоты график данной функции не имеет, так как предел функции при стремлении икса к плюс бесконечности равен плюс бесконечности:
Выясним наличие наклонной асимптоты:
Получили конечные пределы k = 2 и b = 0 . Прямая y = 2x является двусторонней наклонной асимптотой графика данной функции (рис. внутри примера).
Пример 7. Найти асимптоты графика функции
Решение. Функция имеет одну точку разрыва x = −1 . Вычислим односторонние пределы и определим вид разрыва:


Заключение: x = −1 — точка разрыва второго рода, поэтому прямая x = −1 является вертикальной асимптотой графика данной функции.
Ищем наклонные асимптоты. Так как данная функция — дробно-рациональная, пределы при 

Подставляя найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты:
На рисунке график функции обозначен бордовым цветом, а асимптоты — чёрным.
Пример 8. Найти асимптоты графика функции

Решение. Так как данная функция непрерывна, её график не имеет вертикальных асимптот. Ищем наклонные асимптоты:

Таким образом, график данной функции имеет асимптоту y = 0 при 

Пример 9. Найти асимптоты графика функции

Решение. Сначала ищем вертикальные асимптоты. Для этого найдём область определения функции. Функция определена, когда выполняется неравенство 




Рассмотрим правосторонний предел при 

Точка x = 2 — точка разрыва второго рода, поэтому прямая x = 2 — вертикальная асимптота графика данной функции.
Ищем наклонные асимптоты:
Итак, y = x + 1 — наклонная асимптота графика данной функции при 

Итак, y = −x − 1 — наклонная асимптота при 
Пример 10. Найти асимптоты графика функции
Решение. Функция имеет область определения 



Оба предела нашли, используя первый замечательный предел. Заключение: x = 0 — точка устранимого разрыва, поэтому у графика функции нет вертикальных асимптот.
Ищем наклонные асимптоты:
Таким образом, при 


Пример 11. Найти асимптоты графика функции

Решение. Сначала найдём вертикальные асимптоты. Для этого найдём точки разрыва функции и их виды. Знаменатель не может быть равным нулю, поэтому должно соблюдаться условие 


Так как все пределы равны бесконечности, обе точки разрыва — второго рода. Поэтому график данной функции имеет две вертикальные асимптоты: x = 2 и x = −2 .
Ищем наклонные асимптоты. Так как данная функция является дробно-рациональной, пределы при 

Подставляем найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты y = 2x . Таким образом, график данной функции имеет три асимптоты: x = 2 , x = −2 и y = 2x .
Найти асимптоты графика функции самостоятельно, а затем посмотреть решения
Пример 12. Найти асимптоты графика функции 
Пример 13. Найти асимптоты графика функции 
Асимптоты графика функции
Вы будете перенаправлены на Автор24
Достаточно часто на практике приходится иметь дело с функциями, которые определены не на всей числовой прямой, либо принимают не любые значения из множества действительных чисел.
В таких случаях при построении графиков функций получаем, что график функции не является непрерывной линией, а имеет некоторые разрывы. В результате чего становится целесообразным ввести понятие «асимптота».
Асимптота — это такая прямая, к которой график заданной функции приближается сколько угодно близко, но не пересекает ее.
Среди асимптот выделяют следующие виды:
- вертикальная асимптота (параллельна оси ОY);
- горизонтальная асимптота (параллельна оси ОХ);
- наклонная асимптота (расположена под углом к осям координат).
Отметим, что асимптоты на графике функции изображаются пунктирной линией.
Вертикальная асимптота — это прямая, определяемая уравнением $x=a$, для которой выполняются условия $\mathop<\lim >\limits_
Вертикальная асимптота может быть только в точках разрыва функции $y=f(x)$, т.е. в тех точках, где данная функция неопределенна.
Найти вертикальную асимптоту графика данной функции: $y=\frac<5>
Следовательно, прямая $x=2$ является вертикальной асимптотой (см. рис.).
Горизонтальная асимптота — это прямая, определяемая уравнением $y=b$, для которой выполняются условия $\mathop<\lim >\limits_
Готовые работы на аналогичную тему
Найти горизонтальную асимптоту графика данной функции: $y=5^
Следовательно, прямая $y=0$ является горизонтальной асимптотой (см. рис.).
График функции может иметь только правую либо только левую горизонтальную асимптоту.
Наклонная асимптота — это прямая, определяемая уравнением $y=kx+b$, для которой выполняется условие $\mathop<\lim >\limits_
Условия существования наклонной асимптоты определяются следующей теоремой.
Если функция $y=f(x)$ имеет конечные пределы $\mathop<\lim >\limits_
Частным случаем наклонной асимптоты при $k=0$ является горизонтальная асимптота.
Наклонная асимптота может быть левой (график приближается справа), правой (график приближается слева) или двусторонней (график приближается с обоих сторон).
Найти наклонную асимптоту графика данной функции: $y=\frac
Следовательно, прямая $y=x+2$ является наклонной асимптотой (см. рис.). В данном случае имеем двустороннюю наклонную асимптоту.
Найти наклонную асимптоту графика данной функции: $y=\frac
Следовательно, график данной функции не имеет наклонной асимптоты.
График функции может иметь одновременно несколько асимптот, например, вертикальную и наклонную.
Найти асимптоты графика данной функции: $y=\frac <3x^<2>>
Область определения функции: $D_
Следовательно, прямая $x=1$ является вертикальной асимптотой (см. рис.).
Следовательно, прямая $y=3x+3$ является наклонной асимптотой (см. рис.). В данном случае имеем двустороннюю наклонную асимптоту.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 17 02 2022
Асимптоты графиков функций
 Вертикальные асимптоты Вертикальные асимптоты |
 Наклонные асимптоты Наклонные асимптоты |
 Горизонтальные асимптоты как частный случай наклонных асимптот Горизонтальные асимптоты как частный случай наклонных асимптот |
 Поиск наклонных асимптот графиков функций Поиск наклонных асимптот графиков функций |
Вертикальные асимптоты
Во многих разделах нашего справочника приведены графики различных функций. Для многих функций существуют прямые, к которым графики функций неограниченно приближаются. Такие прямые называют асимптотами, и их точное определение мы дадим чуть позже. Как мы увидим далее, асимптоты бывают вертикальными, горизонтальными и наклонными. С вертикальными и горизонтальными асимптотами графика функции мы уже встречались, в частности, в разделе «Гипербола на координатной плоскости. График дробно-линейной функции». С наклонными асимптотами, за исключением горизонтальных, мы пока еще дела не имели.
Определение 1. Говорят, что x стремится к x0 слева и обозначают
Говорят, что x стремится к x0 справа и обозначают
Определение 2. Прямую
называют вертикальной асимптотой графика функции y = f (x) при x , стремящемся к с справа, если функция y = f (x) определена на некотором интервале (с, d) и выполнено соотношение выполнено соотношение
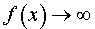
называют вертикальной асимптотой графика функции y = f (x) при x , стремящемся к с слева, если функция y = f (x) определена на некотором интервале (d, c) и выполнено соотношение выполнено соотношение
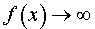
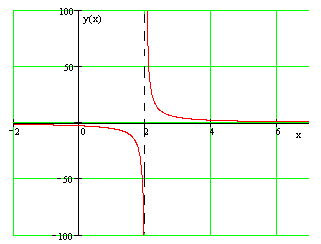
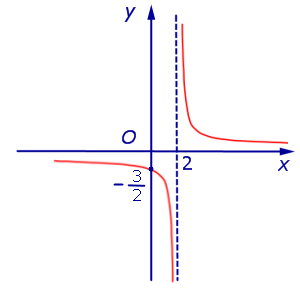
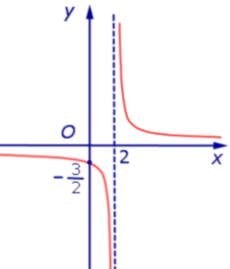
Пример 1. Прямая
является вертикальной асимптотой графика функции
как справа, так и слева (рис. 1)
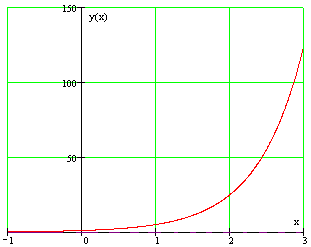
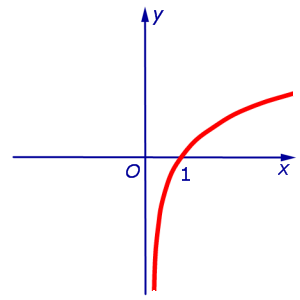
Пример 2. Прямая
является вертикальной асимптотой графика функции
при x , стремящемся к 0 справа (рис. 2)
Наклонные асимптоты
Определение 3. Прямую
называют наклонной асимптотой графика функции y = f (x) при x , стремящемся к 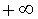
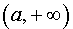
называют наклонной асимптотой графика функции y = f (x) при x , стремящемся к 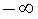
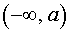
Горизонтальные асимптоты как частный случай наклонных асимптот
Определение 4. Прямую
называют горизотальной асимптотой графика функции y = f (x) при x , стремящемся к 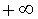
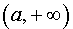
называют горизотальной асимптотой графика функции y f (x) при x , стремящемся к 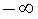
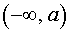
Замечание . Из определений 3 и 5 вытекает, что горизонтальная асимптота является частным случаем наклонной асимптоты y = kx + b, когда угловой коэффициент прямой k = 0 .
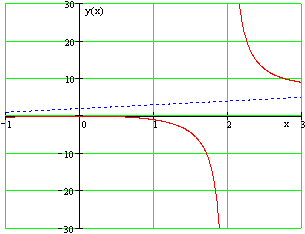
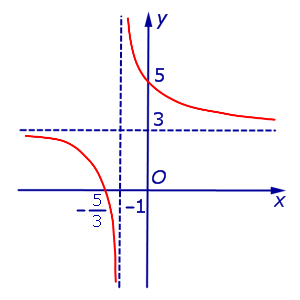
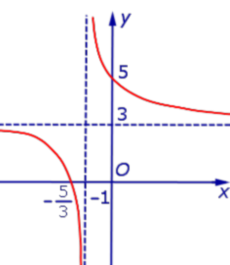
Пример 3. Прямая
является горизонтальной асимптотой графика функции
как при x , стремящемся к 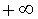
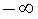
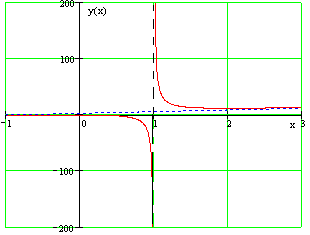
Пример 4. Прямая
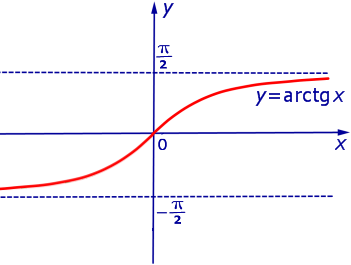
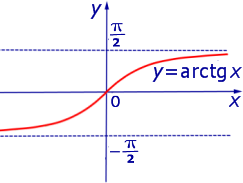
является горизонтальной асимптотой графика функции
при x , стремящемся к 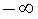
имеет две горизонтальные асимптоты: прямая
является горизонтальной асимптотой графика функции при 
является горизонтальной асимптотой графика функции при 
Поиск наклонных асимптот графиков функций
Для того, чтобы найти наклонную асимптоту графика функции y = f (x) при 

Первая операция. Вычислим предел предел
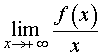 | (1) |
Если предел (1) не существует или существует, но равен существует, но равен 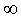

переходим ко второй операции.
Вторая операция. Вычислим предел предел
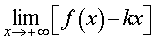 | (2) |
Если предел (2) не существует или существует, но равен существует, но равен 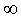

делаем вывод о том, что прямая
является наклонной асимптотой графика функции y = f (x) при 
Совершенно аналогично поступаем для того, чтобы найти наклонную асимптоту графика функции y = f (x) при 

Первая операция. Вычислим предел предел
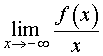 | (3) |
Если предел (3) не существует или существует, но равен существует, но равен 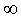

переходим ко второй операции.
Вторая операция. Вычислим предел предел
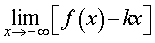 | (4) |
Если предел (4) не существует или существует, но равен существует, но равен 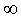

делаем вывод о том, что прямая
является наклонной асимптотой графика функции y = f (x) при 
Пример 5. Найти асимптоты графика функции
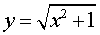 | (5) |
и построить график этой функции.
Решение. Функция (5) определена для всех 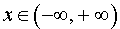
Найдем наклонные асимптоты графика функции (5). При 
Отсюда вытекает, что прямая
– наклонная асимптота графика функции (5) при 
При 
Отсюда вытекает, что прямая
– наклонная асимптота графика функции (5) при 
Итак, y’ > 0 при x > 0 , y’ при x y’ = 0 при x = 0 . Точка x = 0 – стационарная, причем производная функции (5) при переходе через точку x = 0 меняет знак с «–» на «+» . Следовательно, x = 0 – точка минимума функции (5). Других критических точек у функции (5) нет.
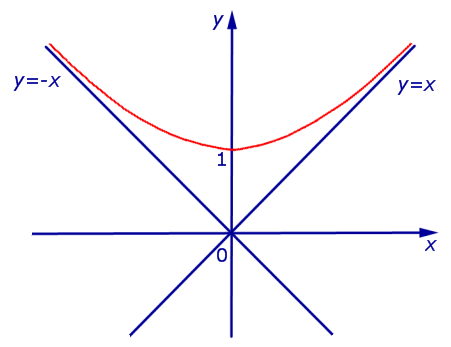
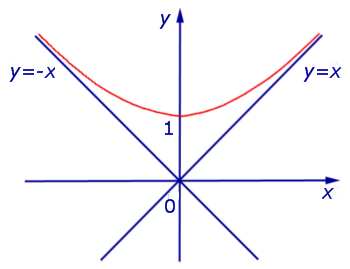
Теперь мы уже можем построить график функции (5):
Заметим, что график функции (5) находится выше асимптот y = x и y =v– x , поскольку справедливо неравенство:
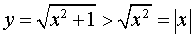
http://spravochnick.ru/matematika/obschiy_plan_issledovaniya_funkciy_i_postroeniya_grafikov/asimptoty_grafika_funkcii/
http://www.resolventa.ru/spr/matan/asymptote.htm
 (предел функции при значении аргумента, стремящимся к некоторому значению a слева, равен плюс или минус бесконечности)
(предел функции при значении аргумента, стремящимся к некоторому значению a слева, равен плюс или минус бесконечности) (предел функции при значении аргумента, стремящимся к некоторому значению a справа, равен плюс или минус бесконечности).
(предел функции при значении аргумента, стремящимся к некоторому значению a справа, равен плюс или минус бесконечности). обозначается стремление x к a справа, причём x остаётся больше a;
обозначается стремление x к a справа, причём x остаётся больше a; обозначается стремление x к a слева, причём x остаётся меньше a.
обозначается стремление x к a слева, причём x остаётся меньше a.