Уравнения прямой, виды уравнений прямой в пространстве
Материал этой статьи продолжает тему прямой в пространстве. От геометрического описания пойдем к алгебраическому: зададим прямую при помощи уравнений в фиксированной прямоугольной системе координат трехмерного пространства. Приведем общую информацию, расскажем о видах уравнений прямой в пространстве и их связи между собой.
Уравнение прямой в пространстве: общие сведения
Уравнение прямой на плоскости в прямоугольной системе координат O x y – это линейное уравнение с переменными x и y , которому отвечают координаты всех точек прямой и не удовлетворяют координаты никаких прочих точек.
Если речь идет о прямой в трехмерном пространстве, все несколько иначе: не существует такого линейного уравнения с тремя переменными x , y , z , которому бы отвечали только координаты точек заданной прямой. В самом деле, уравнение A x + B y + C z + D = 0 , где x , y , z – переменные, а А , В , С и D – некоторые действительные числа ( А , В , С одновременно не равны нулю) – это общее уравнение плоскости. Тогда как же задать прямую линию в прямоугольной системе координат O x y z ? Найдем ответ на этот вопрос в следующих пунктах темы.
Уравнение прямой в пространстве как уравнение двух пересекающихся плоскостей
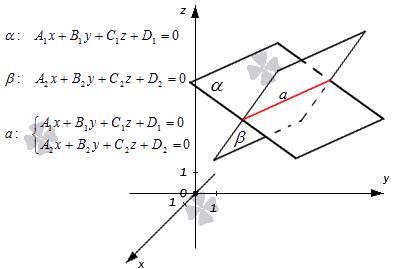
Когда две плоскости в пространстве имеют общую точку, существует их общая прямая, на которой находятся все общие точки этих плоскостей.
Рассмотрим это утверждение в алгебраическом толковании.
Допустим, в трехмерном пространстве зафиксирована прямоугольная система координат O x y z и задано, что прямая a – это линия пересечения двух плоскостей α и β , которые соответственно описываются уравнениями плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . Поскольку прямая a – это множество общих точек плоскостей α и β , то координаты любой точки прямой a будут одновременно отвечать обоим уравнениям. Никакие прочие точки одновременно удовлетворять условия обоих уравнений не будут.
Таким образом, координаты любой точки прямой a в прямоугольной системе координат станут частным решением системы линейных уравнений вида
A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0
Общее же решение системы уравнений _ A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 определит координаты каждой точки прямой a , т.е. по сути задает саму прямую a .
Резюмируем: прямая в пространстве в прямоугольной системе координат O x y z может быть задана системой уравнений двух плоскостей, которые пересекаются:
A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0
Приведем пример описания прямой линии в пространстве при помощи системы уравнений:
x + 3 y — 2 1 z + 11 3 y + 1 4 z — 2 = 0
Навык определения прямой линии уравнениями пересекающихся плоскостей необходим при решении задач на нахождение координат точки пересечения прямой и плоскости или нахождение координат точки пересечения двух прямых в пространстве.
Подробнее изучить эту тему можно, обратившись к статье об уравнениях прямой в пространстве, уравнениях двух пересекающихся прямых.
Заметим, что существует несколько способов описания прямой в пространстве. В практике прямую чаще задают не двумя пересекающимися плоскостями, а направляющим вектором прямой и точкой, принадлежащей этой прямой. В подобных случаях легче задать канонические и параметрические уравнения прямой в пространстве. Поговорим о них ниже.
Параметрические уравнения прямой в пространстве
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , где x 1 , y 1 , z 1 – координаты некой точки прямой; а x , а y и a z (одновременно не равны нулю) – координаты направляющего вектора прямой. а · λ – некий параметр, принимающий любые действительные значения.
Любое значение параметра λ позволяет, используя параметрические уравнения прямой в пространстве, определить тройку чисел ( x , y , z ) , соответствующую некой точке прямой (отсюда и название такого вида уравнений). Например, пусть λ = 0 , тогда из параметрических уравнений прямой в пространстве получим координаты:
x = x 1 + a x · 0 y = y 1 + a y · 0 z = z 1 + a z · 0 ⇔ x = x 1 y = y 1 z = z 1
Рассмотрим конкретный пример:
Пусть прямая задана параметрическими уравнениями вида x = 3 + 2 · a x y = — 2 · a y z = 2 + 2 · a z .
Заданная прямая проходит через точку М 1 ( 3 , 0 , 2 ) ; направляющий вектор этой прямой имеет координаты 2 , — 2 , 2 .
Продолжение изучения этой темы можно найти в статье о параметрических уравнениях прямой в пространстве.
Канонические уравнения прямой в пространстве
Если разрешить каждое из параметрических уравнений прямой
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ относительно параметра λ , возможно просто перейти к каноническим уравнениям прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z .
Канонические уравнения прямой в пространстве задают прямую, которая проходит через точку М 1 ( x 1 , y 1 , z 1 ) , и у которой направляющий вектор равен a → = ( a x , a y , a z ) . Например, задана прямая, описываемая каноническим уравнением x — 1 1 = y 2 = z + 5 7 . Эта прямая проходит через точку с координатами ( 1 , 0 , — 5 ) , ее направляющий вектор имеет координаты ( 1 , 2 , — 7 ) .
Отметим, что одно или два числа из чисел а x , а y и а z в канонических уравнениях прямой могут быть равны нулю (все три числа не могут быть равны нулю, поскольку направляющий вектор не может быть нулевым). В таком случае запись вида x — x 1 a x = y — y 1 a y = z — z 1 a z является формальной (поскольку в знаменателях одной или двух дробей будут нули) и понимать ее нужно как:
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , где λ ∈ R .
Если одно из чисел а x , а y и a z канонического уравнения прямой равно нулю, то прямая лежит в какой-то из координатных плоскостей, или в плоскости, ей параллельной. Если два из чисел а x , а y и a z равны нулю, то прямая или совпадает с какой-либо из координатных осей, или параллельна ей. К примеру, прямая, описываемая каноническим уравнением x + 4 3 = y — 5 2 = z + 2 0 , лежит в плоскости z = — 2 , параллельной координатной плоскости O x y , а координатная ось O y описывается каноническими уравнениями x 0 = y 1 = z 0 .
Графические иллюстрации подобных случаев, составление канонических уравнений прямой в пространстве, примеры решения типовых задач, а также алгоритм перехода от канонических уравнений к другим видам уравнений прямой в пространстве рассмотрены в статье о канонических уравнениях прямой в пространстве.
Уравнение прямой
Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
где A и B не могут быть одновременно равны нулю.
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.
Уравнение прямой в отрезках на осях
Если прямая пересекает оси OX и OY в точках с координатами ( a , 0) и (0, b ), то она может быть найдена используя формулу уравнения прямой в отрезках
| x | + | y | = 1 |
| a | b |
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки M( x 1, y 1) и N( x 2, y 2), такие что x 1 ≠ x 2 и y 1 ≠ y 2, то уравнение прямой можно найти, используя следующую формулу
| x — x 1 | = | y — y 1 |
| x 2 — x 1 | y 2 — y 1 |
Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
x = l t + x 0 y = m t + y 0
где N( x 0, y 0) — координаты точки лежащей на прямой, a = < l , m >— координаты направляющего вектора прямой.
Каноническое уравнение прямой на плоскости
Если известны координаты точки N( x 0, y 0) лежащей на прямой и направляющего вектора a =
| x — x 0 | = | y — y 0 |
| l | m |
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
x — 1 2 — 1 = y — 7 3 — 7
Упростив это уравнение получим каноническое уравнение прямой
Выразим y через x и получим уравнение прямой с угловым коэффициентом
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
x = t + 1 y = -4 t + 7
Решение. Так как M y — N y = 0, то невозможно записать уравнение прямой проходящей через две точки.
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Уравнение прямой в пространстве
Уравнение прямой, проходящей через две различные точки в пространстве
Если прямая проходит через две точки M( x 1, y 1, z 1) и N( x 2, y 2, z 2), такие что x 1 ≠ x 2, y 1 ≠ y 2 и z 1 ≠ z 2, то уравнение прямой можно найти используя следующую формулу
| x — x 1 | = | y — y 1 | = | z — z 1 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 |
Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
 | x = l t + x 0 |
| y = m t + y 0 | |
| z = n t + z 0 |
где ( x 0, y 0, z 0) — координаты точки лежащей на прямой,
Каноническое уравнение прямой в пространстве
Если известны координаты точки M( x 0, y 0, z 0) лежащей на прямой и направляющего вектора n =
| x — x 0 | = | y — y 0 | = | z — z 0 |
| l | m | n |
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
Ортогональнальная проекция прямой на плоскость.
Угол между прямой и плоскостью.
Теорема о трех перпендикулярах
 Проекция точки на плоскость. Проекция прямой на плоскость Проекция точки на плоскость. Проекция прямой на плоскость |
 Угол между прямой и плоскостью Угол между прямой и плоскостью |
 Теорема о трех перпендикулярах. Обратная теорема Теорема о трех перпендикулярах. Обратная теорема |
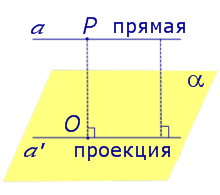
Проекция прямой на плоскость
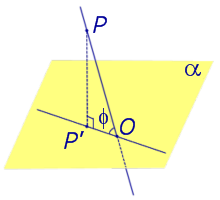
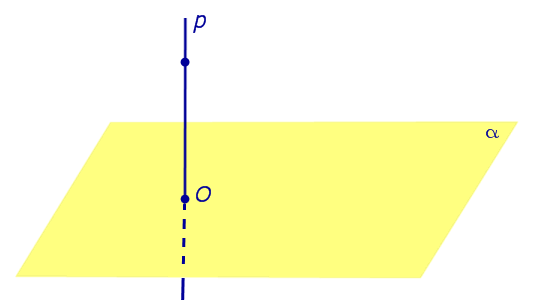
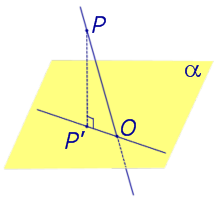
Определение 1. Ортогональной проекцией точки на плоскость называют основание перпендикуляра, опущенного из этой точки на плоскость.
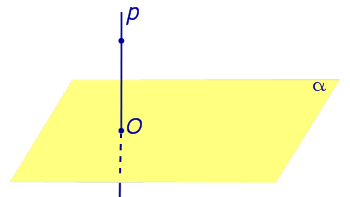
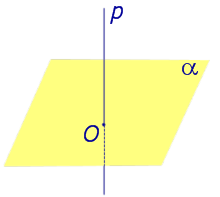
Рассмотрим рисунок 1, на котором изображены прямая p, перпендикулярная к плоскости α и пересекающая плоскость α в точке O.
Точка O является ортогональной проекцией на плоскость α каждой точки прямой p.
Замечание 1. Рассматриваемый в данном разделе случай ортогонального проектирования точки на плоскость α представляет собой частный случай более общего понятия проектирования точки на плоскость параллельно некоторой прямой, необязательно перпендикулярной к плоскости. Такое проектирование используется в нашем справочнике при определении понятия «призма».
Замечание 2. Если это не приводит к разночтениям, для упрощения формулировок термин «ортогональная проекция на плоскость» часто сокращают до термина «проекция на плоскость».
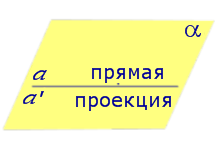
Определение 2. Проекцией фигуры a на плоскость α называют фигуру a’, образованную проекциями всех точек фигуры a на плоскость α.
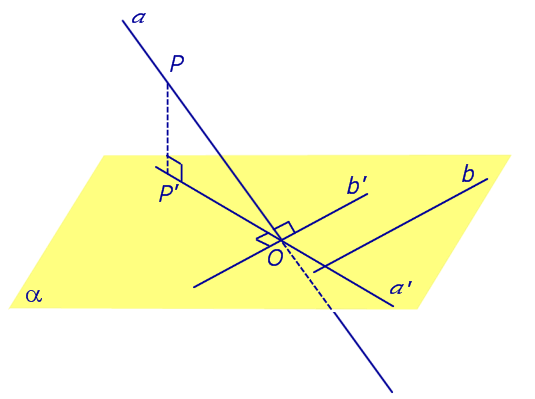
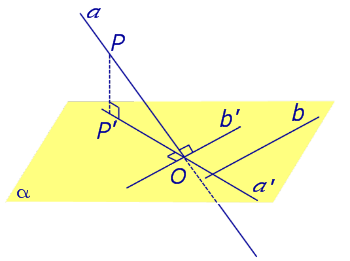
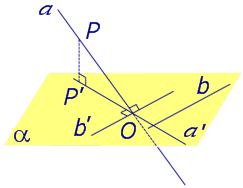
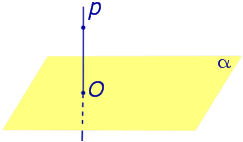
Определение 3. Прямую, пересекающую плоскость и не являющуюся перпендикуляром к плоскости, называют наклонной к этой плоскости (рис. 2).
Все возможные случаи, возникающие при ортогональном проектировании прямой на плоскость представлены в следующей таблице
| Фигура | Рисунок | Свойство проекции | ||||||||||
| Наклонная к плоскости α | 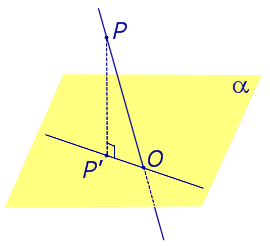 | |||||||||||
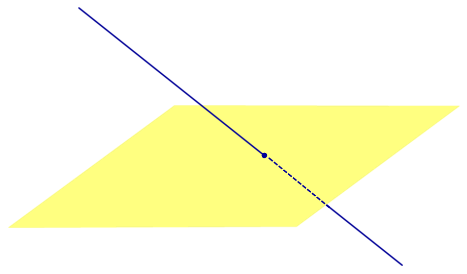
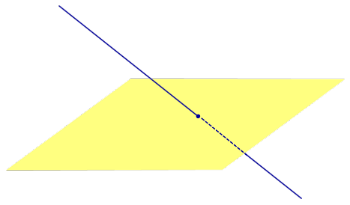
| Прямая, параллельная плоскости | 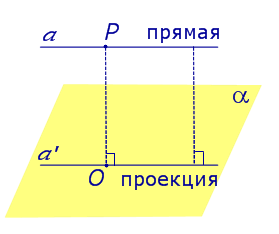 | |||||||||||
| Прямая, лежащая на плоскости | 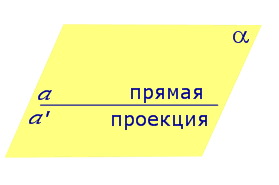 | |||||||||||
| Прямая, перпендикулярная к плоскости | 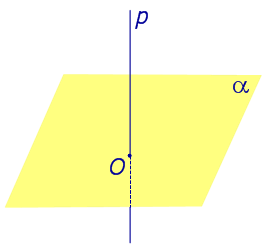 |
| Фигура | Рисунок | Определение |
| Наклонная к плоскости α | 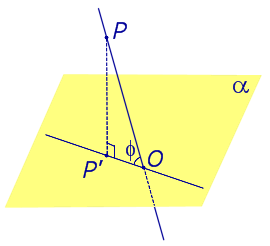 | |
| Прямая, параллельная плоскости | 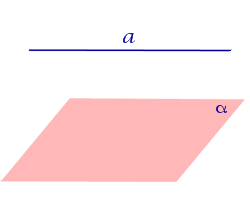 | |
| Прямая, лежащая на плоскости |  | |
| Прямая, перпендикулярная к плоскости | 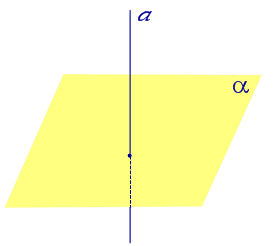 |





 радиан).
радиан).