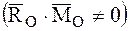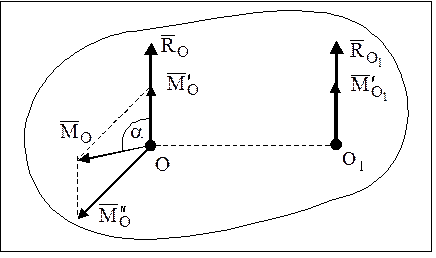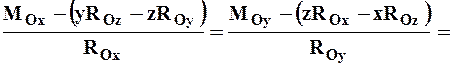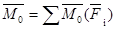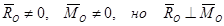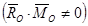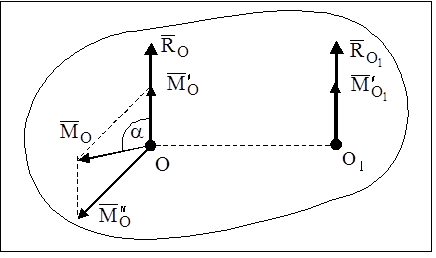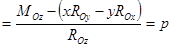Уравнение центральной винтовой оси




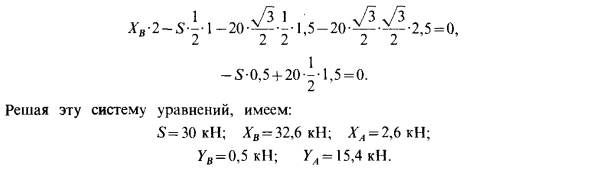
Уравнение центральной винтовой оси
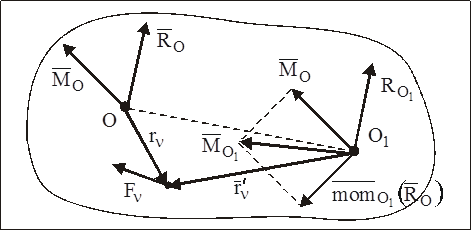
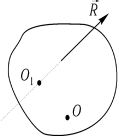
- Предположим, что главный вектор Lo проецируется на координатные оси Rx, Ry и Rz, а главный момент Lo получается на проекции Lx и Ly с центром редукции ^ в качестве начала координат. Когда система сил движется к центру редукции O (рис. 78), обнаруживается динамо с главным вектором A, = A и главным моментом LOl. Векторы LO1 и A, как генераторы динамо, параллельны, поэтому отличается только скалярный коэффициент k0. У нас есть Lo-k0R, _ _ (9) Согласно (2), поскольку Rt = R, основные моменты LOi и Lo удовлетворяют следующему соотношению: EOi = Lo
OO, xR. (2 ‘) Подставляя LOi из (2 ‘) в (9) Lo-Od, xR = knR. (9 ‘) Координаты точки O, из которой получается динамо, обозначены x, y, z.
Тогда проекция вектора OOt на оси координат равна координатам x, y, r. Учитывая это, (9 ‘) можно выразить в следующем виде: (Lxi + Lj + LZE) -x Jy AH A, = k0 (Rxi + Ryj + Rjc), Aj Где i, j и А — единичные векторы векторного произведения осей координат и OO, а x A выражается определителем. Векторное уравнение (9 «) соответствует трем скалярным уравнениям и может быть выражено следующим образом после отбрасывания Lo: £, — (yY, -? I,) _ £, — (rY, -xY,) _ I, I, (9 «) Рисунок 78 Рис. 79 Линейное уравнение (10) для координат x, y и z является уравнением спиральной оси с линейным центром. Таким образом, в точке, где система сил сводится к двойственности, есть прямая линия. Пример 1.
Такая линеаризация, конечно, в некоторой степени искажает действительное изображение движения, но чем меньше отклонение системы от устойчивого положения равновесия, тем точнее получается линеаризованное изображение. Людмила Фирмаль
В конце куба с длиной стороны 1 = 3 м действуют силы Fj = Fr = 2_H и F3 = l H (рис. 79). Приносит систему питания F, F2. Е3 в простейшем виде. Решения. Выберите точку O (начало координат) в качестве центра уменьшения силы и рассчитайте главный вектор R и главный момент Lo. для Проекции на оси этих векторов K = Y.Fix = F2 = 2B; Rr = ^ Flt = F3 = i H-. Rn- £ /? = £, = 2 H; ix = XWx (F;) = 0; Координаты у нас есть: Z.z = £ m, (F) = F3 / -F2 / = -3Hm.
Значение основного вектора и значение главного момента составляют R = ^ R2x + R ^ + R ^ = y / 9 = 3 Н. £ 0 = V / ZJ + ZJ + IJ = V / 45 = 6,8 Нм Определите угол a между векторами Eo и R. Для этого сформируем скалярное произведение. Это выражается в двух формах: Eo-R = LoRcos
- Один конец — это сечение _A, и нормальная сила P прикладывается в точке B (рис. 81, а). Надежно прикрепите балку CD к балке AB секции C под прямым углом. На конце балки I в плоскости, параллельной координатной плоскости Ayz, действует пара сил с моментом M = Ra. Направление вращения пары размеров и сил показано на рисунке. Определяет момент силы пары вложенных сил. Решения. Лучи B и CD, рассматриваемые вместе, освобождаются от галстуков. Вложение системы пространства сил создает неизвестную силу Ra, спроецированную на ось координат силы X с вектором. Момент Отологон Динат М.Л., (Рисунок £ Flx = 0; * l = 0; £ f (, = 0; ya = Q; £ F „= 0; ZA — P = O; Y.
Для того, чтобы определить силу реакции упорного подшипника, п Людмила Фирмаль
Что касается проекции сил на оси координат, то здесь есть следующее. EG (x = 0;% 4 + Uv-Psin asin p-Ssiny = 0; 1 EFf = 0; Ul + rB + Pcosa-Scosy = 0;> EF (, = 0; Z4-Psin acos P = 0. При определении проекции силы P на оси координат сначала разбейте ее на две вертикальные составляющие. Одна параллельна оси Oy и имеет проекцию на эту ось P = Pcosa. Вертикальный компонент расположен в плоскости оси и имеет проекционное значение в этой плоскости. (А) Спроецируйте силу P как вектор на оси Ax и Ar. В P, = -P „sin p = -Psin a sin p; P, = P„ cosp = Psinacosp.
За момент силы вокруг осей получим … МЖ (Р,) = О; -Gv (/, + / 2) + Scosy /, -Pcosa (Z, + / 2 + / 3) = 0;] EM, (A) = 0; XB (Z, + / 2) -Ссины / 1- Я -Psin acos pZ „-Psin asin p (Z, + 12 + Z3) = 0; EA / I (F,) = 0; -SP + PcosaZ4 = 0. По определению, при расчете момента силы вокруг координатной оси, спроецируйте силу на плоскость, перпендикулярную оси, и рассчитайте момент проекции силы относительно пересечения оси и плоскости. Сила, параллельная или пересекающая ось, дает нулевой момент вокруг этой оси.
При определении момента силы S для осей координат он разлагается на компоненты, параллельные осям координат, вычисляет момент каждого компонента для соответствующих координатных осей на основе теоремы Баринона и добавляет их алгебраически. Значения составляющих сил равны проекции этих сил на оси и могут быть получены из уравнения (а). Момент силы R. рассчитывается аналогично. Решите систему линейных уравнений (а) и (б) для проекции неизвестных сил. Могу решить Подставляя уравнение (а) и угол, оно становится следующим.
Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Приведение системы сил к динаме
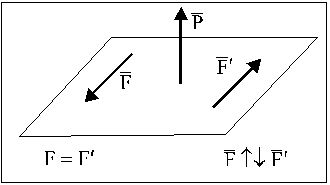
Определение: Система, состоящая из силы и пары сил, момент которой коллинеарен силе (плоскость пары перпендикулярна линии действия силы), называется динамой или динамическим винтом (рис. 30) .
Если при приведении системы сил к центру О второй инвариант не равен нулю, то эта система сил приводится к динаме (рис. 31).
Разложив 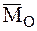
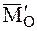
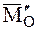
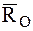
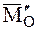
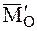
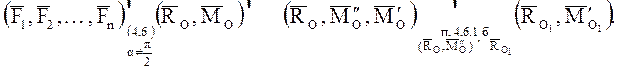
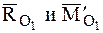
где 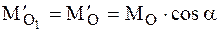
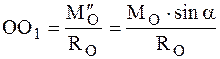
В рассматриваемом случае приведения системы сил главный момент 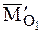
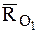
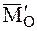
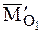
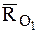
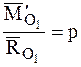
В соответствии с соотношениями (4.16) и (4.17)
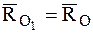
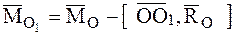
тогда уравнение центральной оси динамы в векторной форме можно записать так:
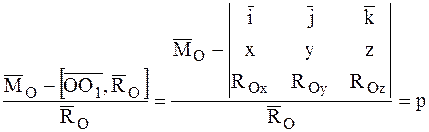
Проектируя это соотношение на оси декартовой системы координат с началом в центре приведения О, получим:
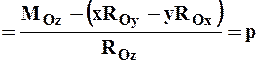
Здесь x, y, z – координаты точек, лежащих на центральной оси, а р – постоянная линейная величина, называемая параметром динамы.
4.7. Алгоритм решения задач по приведению систем сил к простейшим системам – схема алгоритма
Дата добавления: 2015-08-01 ; просмотров: 2401 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Приведение системы сил к заданному центру.
Лекция 3
Краткое содержание: Приведение произвольной и плоской системы сил к центру. Теорема о параллельном переносе силы, основная теорема статики Приведении системы сил к данному центру Главный вектор и главный момент системы сил. Зависимость главного момента от выбора центра. Аналитическое определение главного вектора и главного момента системы сил. Инварианты системы сил. Приведение системы сил к простейшему виду. Частные случаи приведения произвольной системы сил, динамический винт. Теорема Вариньона о моменте равнодействующей.
Приведение силы к заданному центру (Лемма Пуансо)

Лемма Пуансо о параллельном переносе силы.. Не изменяя действия силы на твердое тело, ее можно переносить параллельно самой себе в любую точку тела, добавляя при этом пару, момент которой равен моменту данной силы относительно новой точки приложения.
Пусть сила 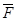

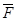


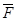


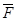
Приведение системы сил к заданному центру.
Главным вектором системы сил называется вектор, равный векторной сумме этих сил.
Главным моментом системы сил относительно точки О тела, называется вектор, равный векторной сумме моментов всех сил системы относительно этой точки.
Теорема Пуансо (Основная теорема статики)
Произвольную систему сил, действующую на твердое тело, можно заменить эквивалентной системой, состоящей из силы и пары сил. Сила равна главному вектору системы сил и приложена в произвольно выбранной точке (центре приведения), момент пары равен главному
моменту системы сил относительно этой точки.
Точка О — центр приведения. По лемме Пуансо перенесем силу F1 в точку О. При этом вместо F1 имеем в точке О такую же силу F1’ и дополнительно пару сил с моментом m1.
Аналогично перенесем все остальные силы. В результате получим систему сходящихся сил и систему пар сил. По теореме о существовании равнодействующей системы сходящихся
сил их можно заменить одной силой R, равной главному вектору. Систему пар по теореме о сложении пар можно заменить одной парой, момент которой равен главному моменту Mo. ■
Инварианты статики — характеристики системы сил, не зависящие от выбора центра приведения.
Первый инвариантстатики — главный вектор системы сил (по определению).
Второй инвариантстатики — скалярное произведение главного вектора и главного момента.
В самом деле, главный момент, очевидно, зависит от выбора центра приведения. Рассмотрим произвольную систему сил 
Из рисунка видно ,что 
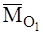
Или 
Домножим обе части этого равенства на 

свойству смешанного произведения векторов 

Если воспользоваться определением скалярного произведения, то для второго инварианта можно получить еще одну форму:

Так как 

Таким образом, проекция главного момента на направление главного вектора есть величина постоянная для данной системы сил и не зависит от выбора центра приведения.
Частные случаи приведения произвольной системы сил к простейшему виду
1) Если при приведении системы сил к центру О 

В этом случае система сил приводится к равнодействующей, приложенной в центре приведения и совпадающей по величине и направлению с главным вектором.
2)Если при приведении системы сил к центру О
то представив 
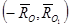
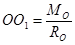
получим: 
В этом случае система сил приводится к равнодействующей, совпадающей по величине и направлению с главным вектором, а линия действия равнодействующей отстоит от линии действия главного вектора на расстоянии 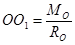
3)Если при приведении системы сил к центру О 

4)Если при приведении системы сил к центру О 

4)
Определение: Система, состоящая из силы и пары сил, момент которой коллинеарен силе (плоскость пары перпендикулярна линии действия силы), называется динамой или динамическим винтом.
Если при приведении системы сил к центру О второй инвариант не равен нулю, то эта система сил приводится к динаме.
Разложив 





Вектора 


В рассматриваемом случае приведения системы сил главный момент 





С учетом 

уравнение центральной оси в векторной форме можно записать так:
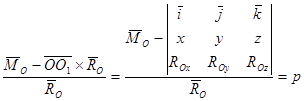
Проектируя это соотношение на оси декартовой системы координат с началом в центре приведения О, получим:
Здесь x, y, z – координаты точек, лежащих на центральной оси, а р – постоянная линейная величина, называемая параметром динамы.
Теорема Вариньона.
Пусть 


но 

http://helpiks.org/4-41341.html
http://lektsii.org/11-51576.html