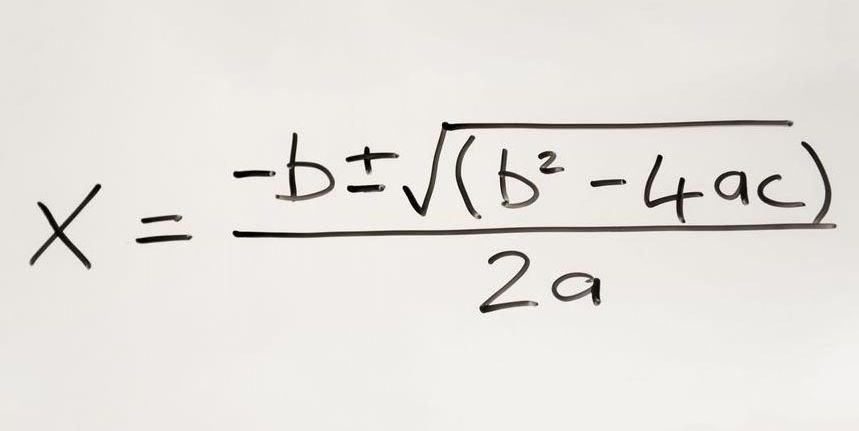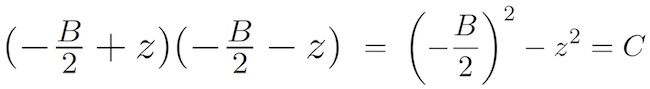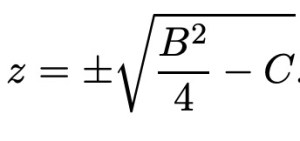Что то новое в квадратных уравнениях

«Уравнение – это золотой ключ, открывающий все математические сезамы»

Математическое образование, получаемое в школе, очень важная часть жизни современного человека. Практически всё, что окружает нас так или иначе связано с математикой. Решение многих практических задач сводится к решению уравнений различных видов.

Уравнения – это наиболее объёмная тема всего курса алгебры. В прошлом учебном году на уроках алгебры мы познакомилась с квадратными уравнениями. Квадратные уравнения находят широкое применение при решении различных задач, как в области математики, так и в области физики и химии.

В школьном курсе математики изучается основные способы решения квадратных уравнений. Однако, имеются и другие приёмы решения квадратных уравнений, некоторые из которых позволяют быстро, рационально решать их.

Нами было проведено анкетирование среди 84 учащихся 8-9 классов по двум вопросам:

Какие способы решения квадратных уравнений вы знаете?

Какие вы используете чаще всего?

По результатам анкетирование были получены следующие результаты:

Проанализировав полученные результаты, мы пришли к выводу, что большинство учащихся используют при решении квадратных уравнений формулы корней с использование дискриминанта и недостаточно осведомлены о способах решения квадратных уравнений.

Таким образом, выбранная нами тема является актуальной.

Мы поставили перед собой цель: изучить нетрадиционные способы решения квадратных уравнений, познакомить учащихся 8 и 9 классов с различными способами решения, выработать умение выбирать рациональный способ решения квадратного уравнения.

Для достижения указанной цели нужно решить следующие задачи:

собрать информацию о различных способах решения квадратных уравнений,

освоить найденные способы решения,

составить программу для решения квадратных уравнений по формулам корней квадратного уравнения в Excel,

разработать дидактический материал для проведения урока или внеурочного мероприятия по нестандартным методам решения квадратных уравнений,

провести занятие «Необычные способы решения квадратных уравнений» с учащимися 8 – 9 классов.

Объект исследования: квадратные уравнения.

Предмет исследования: различных способы решения квадратных уравнений.

Считаем, что практическая значимость работы состоит в возможности использования банка приёмов и способов решения квадратных уравнений на уроках математики и внеурочной деятельности, а также в ознакомлении учащихся 8 — 9 классов с данных материалом.

ГЛАВА 1. НЕОБЫЧНЫЕ МЕТОДЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ

1. СВОЙСТВА КОЭФФИЦИЕНТОВ (a,b,c)

Метод основан на свойствах коэффициентов a,b,c:

Пример:

Справедливы следующие зависимости коэффициентов a,b,c:

Решим следующие уравнения:

Коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Далее корни находятся по теореме Виета. Найденные корни делятся на ранее переброшенный коэффициент, благодаря этому мы находим корни уравнения.

Пример:

«Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение

Согласно теореме Виета

Если в уравнении аx 2 + bx + c = 0 перенести второй и третий члены в правую часть, то получим ax 2 = –bx–c .

Построим графики зависимостей у = aх 2 и у = –bx–c в одной системе координат.

График первой зависимости – парабола, проходящая через начало координат. График второй зависимости – прямая.

Возможны следующие случаи:

прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;

прямая и парабола могут касаться (только одна общая точка), т.е. уравнение имеет одно решение;

прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.

Решим следующие уравнения:

1) х 2 + 2х – 3 = 0

В одной системе координат построим график функции у =х 2 и график функции у = — 2х+3. Обозначив абсциссы точек пересечения, получим ответ.

В одной системе координат построим график функции у = х 2 и график функции у = -6х — 9. Обозначив абсциссу точки касания, получим ответ.

В одной системе координат построим график функции у =2х 2 и график функции

Парабола у =2х 2 и прямая у = — 4х — 7 не имеют общих точек, следовательно уравнение не имеет корней.

Ответ: нет корней.

1. РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ ЦИРКУЛЯ И ЛИНЕЙКИ

Решим уравнение aх 2 +bх+c=0:

Построим точки S(-b:2a,(a+c):2a)- центр окружности и точку А(0,1).

Провести окружность радиуса SA.

Абсциссы точек пересечения с осью Ох есть корни исходного уравнения.

При этом возможны три случая:

1) Радиус окружности больше ординаты центра (AS>SK, или R>), окружность пересекает ось Ох в двух точках..B(х₁; 0) и D(х₂;0), где х₁ и х₂ – корни квадратного уравнения ах 2 + bх + с = 0.

2) Радиус окружности равен ординате центра (AS = SВ, или R = ), окружность касается оси Ох в точке B(х₁; 0 ), где х₁ – корень квадратного уравнения.

3) Радиус окружности меньше ординаты центра (AS SВ или R > , б) AS = SВ или R = в) AS 2 –8х + 6 = 0.

Решение: Определим координаты точки центра окружности по формулам:

Проведём окружность радиуса SA, где А (0;1).

Пример 2: х 2 –6х + 9 = 0.

Решение: Найдём координаты S: x=3, y=5.

Пример 3: х 2 + 4х + 5 = 0.

Решение: Координаты центра окружности: х= — 2 и y = 3.

Ответ: нет корней

Номограмма (от греческого «nomos» – закон и грамма), графическое представление функции от нескольких переменных, позволяющее с помощью простых геометрических операций (например, прикладывание линейки) исследовать функциональные зависимости без вычислений. Например, решать квадратное уравнение без применения формул.

Это старый и в настоящее время забытый способ решения квадратных уравнений, помещённый на стр. 83 сборника: Брадис В.М. «Четырехзначные математические таблицы». — М., “ДРОФА”, 2000. Таблица XXII. Номограмма для решения уравнения z 2 + pz + q = 0 (см. Приложение 1).

Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.

Криволинейная шкала номограммы построена по формулам: ОВ = , АВ =

Полагая ОС = р, ЕD = q, ОЕ = а (все в см), из подобия треугольников САН и СDFполучим пропорцию откуда после подстановок и упрощений вытекает уравнение z 2 + pz + q = 0, причем буква z означает метку любой точки криволинейной шкалы.

Пример 1:z 2 — 9z + 8 = 0.

На шкале p находим отметку -9, а на шкале q отметку 8. Проводим через эти метки прямую, которая пересекает кривую шкалу номограммы в отметках 1 и 8. Следовательно, корни уравнения 1 и 8.

Именно данное уравнение решено в таблице Брадиса стр. 83 (см. Приложение 1).

Пример 2: 2z 2 — 9z + 2 = 0.

Разделим коэффициенты этого уравнения на 2, получим уравнение:

Пример 3:x 2 – 25x + 66 = 0

Коэффициенты p и q выходят за пределы шкалы. Выполним подстановку x = 5z, получим уравнение:

которое решаем посредством номограммы.

Пример 4: z 2 + 5z – 6 = 0, номограмма даёт положительный корень z₁=1, а отрицательный корень находим, вычитая положительный корень из — p, т.е. z₂= — p –1= — 5 – 1= -6.

Пример 5: z 2 – 2z – 8 = 0, номограмма даёт положительный корень z₁=4, а отрицательный равен z₂= — p –4 =

ГЛАВА 2. РЕШЕНИЕ КВАДРАТНОГО УРАВНЕНИЯ ПО ФОРМУЛАМ КОРНЕЙ С ПОМОЩЬЮ EXCEL

Мы решили составить программу для решения квадратного уравнения с помощью Excel – это широко распространенная компьютерная программа. Нужна она для проведения расчётов, составления таблиц и диаграмм, вычисления простых и сложных функций. Она входит в состав пакета Microsoft Office.

Лист программы Excel, где отображены формулы:

Лист программы Excel, где показан конкретный пример решения квадратного уравнения x 2 – 14x – 15 = 0:

ГЛАВА 3. СРАВНЕНИЕ РАЗНЫХ СПОСОБОВ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ

Формула корней квадратного уравнения с использованием дискриминанта D и D1

Универсальность, т.к. можно использовать для решения абсолютно всех квадратных уравнений

Громоздкий дискриминант, не входящий в таблицу квадратов

Быстрота решения в определённых случаях и экономия времени

Если дискриминант не является полным квадратом целого числа.

Не целые коэффициенты b и с.

Выделение полного квадрата

При правильном преобразовании в квадрат двучлена получаем квадратное уравнение неполного вида и следовательно быстрее находятся корни

Сложность выделения полного квадрата при дробных коэффициентах уравнения

Можно решить, не зная формул

Не всегда среднее слагаемое удаётся разложить на подходящие слагаемые для группировки

Не требуется формул.

Можно быстро узнать количество корней уравнения

Свойства коэффициентов a,b,c

Для уравнений с большими коэффициентами

Подходит только для некоторых уравнений

«Переброс» главного коэффициента

Быстрота решения, если корни целые

Такие же как с помощью теоремы Виета

Все, что требуется для решения–это номограмма

Не всегда имеется с собой номограмма.

Нахождение корней с помощью циркуля и линейки

Если координаты центра нецелые числа.

Нахождении корней уравнений с большими коэффициентами

ЗАКЛЮЧЕНИЕ

«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путём сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт»

Уолтер Варвик Сойер

В ходе работы мы собрали материал и изучили способы решения (нахождения корней) квадратных уравнений. Решение уравнений разными способами представлено в Приложении 2.

Изучая разные способы решения квадратных уравнений, мы сделали вывод, что для каждого уравнения можно подобрать свой наиболее эффективный и рациональный вариант нахождения корней. Каждый из способов решения уникален и удобен в определённых случаях. Некоторые способы решения позволяют сэкономить время, что немаловажно при решении заданий на ОГЭ, другие – помогают решить уравнение с очень большими коэффициентами. Мы постарались сравнить разные способы решения, составив таблицу, в которой отразили плюсы и минусы каждого из способов.

Нами разработан раздаточный материал. Познакомиться с банком заданий по теме можно в Приложении 3.

Используя Microsoft Excel, мы составили электронную таблицу, которая позволяет автоматически рассчитывать корни квадратного уравнения по формулам корней.

Мы провели урок, посвященный необычным способам решения квадратных уравнений, для учащихся 9 классов. Ученикам очень понравились способы, они отметили, что полученные знания пригодятся им в дальнейшем обучении. Результатом проведённого урока стали работы учащихся, в которых они представили различные варианты решения квадратных уравнений (см. Приложение 4).

Материал нашей работы можно рекомендовать для внеклассных и факультативных занятий по математике. Учителя могут использовать его для небольшого элективного курса «Необычные способы решение квадратных уравнений».

Материалом работы могут воспользоваться и те, кто любит математику и те, кто хочет знать о математике больше.

Брадис В. М. «Четырехзначные математические таблицы для средней школы», М.: Дрофа, 2000.

Виленкин Н.Я. «Алгебра для 8 класса», М.: Просвещение, 2000.

Галицкий М.Л. «Сборник задач по алгебре», М.: Просвещение 2002.

Глейзер Г. И. «История математики в школе», М.: Просвещение, 1982.

Звавич Л.И. «Алгебра 8 класс», М.: Мнемозина, 2002.

Макарычев Ю.Н. “Алгебра 8 класс”, М.: Просвещение, 2015.

Плужников И. «10 способов решения квадратных уравнений» // Математика в школе. — 2000.- № 40.

Пресман А.А. «Решение квадратного уравнения с помощью циркуля и линейки»//М., Квант, №4/72, c.34.

Савин А.П. «Энциклопедический словарь юного математика»,

М.: Педагогика, 1989.

Интернет ресурсы:

«СБОРНИК БРАДИСА В.М.»

«РЕШЕНИЕ УРАВНЕНИЯ ВСЕМИ СПОСОБАМИ»

Исходноеуравнение: 4х 2 +3х -1 = 0.

1.Формула корней квадратного уравнения с использованием дискриминанта D

D = b 2 – 4ac = 9+16 = 25 > 0, => уравнение имеет два корня

4х 2 +3х -1 = 0, поделим уравнение на 4, чтобы оно стало приведённым

3. Метод выделения полного квадрата

(2х + — )( 2х + + )=0, произведение =0, когда один из множителей=0

4. Способ группировки

(4х-1)( х+1)=0, произведение =0, когда один из множителей=0

5. Свойства коэффициентов

6. Метод «переброски» главного коэффициента

Разделим найденные корни на главный коэффициент и получим корни нашего уравнения:

7. Способ решения квадратных уравнений с помощью циркуля и линейки

Определим координаты точки центра окружности по формулам:

8. Графический способ решения

В одной системе координат построим график функции у = 4х 2 и график функции

у = — 3х+1. Обозначив абсциссы точек пересечения, получим ответ:

9. С помощью номограммы

4х 2 +3х -1 = 0, разделим коэффициенты уравнения 1/на 4, получим уравнение

Номограмма даёт положительный корень = ,

а отрицательный корень находим, вычитая положительный корень из — p, т.е.

10. Решение данного уравнения в EXCEL

«ДИДАКТИЧЕСКИЙ МАТЕРИАЛ ДЛЯ ТЕМЫ

“РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ”»

Самый простой способ решения квадратичных уравнений упускается из виду в течение 4000 лет

Профессор математики открыл новый способ решения квадратных уравнений. Это вычислительно эффективнее и проще для запоминания, чем традиционная квадратичная формула. Удивительно, что такой простой метод оставался незамеченным в течение 4000 лет.

В элементарной алгебре квадратные уравнения могут быть решены с использованием различных методов, таких как факторинг, построение графиков, построение квадратов и другие.

История квадратичной формулы — формула обеспечивает решение (я) квадратного уравнения — может быть прослежена до древне-вавилонского периода около 2000–1600 гг. До н.э. Многие великие математики оставили свой след на этом предмете, и формула стала одной из самых важных частей в алгебре.

Формула, однако, довольно сложна, и ее вычисления несколько запутаны. Это может быть сложной задачей для начинающих изучающих алгебру.

Недавно математик из Университета Карнеги-Меллона в Питтсбурге опубликовал более простое решение для любого квадратного уравнения. Этот новый метод прост в запоминании и эффективен в вычислительном отношении.

По словам его автора, По-Шен Ло , он имеет потенциал для демистификации квадратичной формулы для студентов во всем мире.

Альтернативный метод решения квадратичных задач

Самый первый шаг — посмотреть, можно ли разложить квадратное уравнение следующим образом:

Если факторизация возможна, то квадратичная функция равна нулю при X=R или X=S. Согласно традиционному методу, если сумма и произведение R и S равно -B и C соответственно, то будет полным набором корней.

А вот теперь начинается поворот.

Два числа суммируют с -B именно тогда, когда их среднее значение равно -B / 2. Рассмотрим эти два числа в виде -B / 2 ± z, где z — неизвестная величина, а произведение этих чисел равно C.

Если z оказывается равным нулю, то мы разложим с R = S = (- B / 2), в противном случае,

Квадратный корень всегда существует (с учетом комплексных чисел), поэтому искомые R и S всегда существуют для любого квадратичного уравнения. Таким образом, исходные корни могут быть выражены как

А, это новая квадратичная формула; гораздо проще и легче запомнить, чем предыдущий.

Почему сейчас?

Новый метод интуитивно понятен и не требует запоминания формулы вообще. Однако, более интересный вопрос, почему никто не думал об этом раньше.

Автор исследовал 4000-летнюю историю по этой теме: он изучал различные подходы, построенные древними вавилонянами, греками, индийцами, арабами и китайцами, а также современными математиками, но не нашел ничего похожего на его метод.

По-Шен Ло считает, что это связано с тем, как традиционный метод доказывает, что квадратные уравнения имеют два корня. Обычно считается, что квадратное уравнение всегда имеет два корня, и эти корни имеют произведение C и -B.

Возможно, к тому времени, когда математика продвинулась до «приличного уровня», Вавилонская техника исчезла из недавней памяти, и люди нашли подход завершения квадрата достаточно хорошим, чтобы интегрироваться в основную учебную программу.

Теперь вопрос в том, как быстро и насколько широко он будет распространяться.

Как решать квадратные уравнения

О чем эта статья:

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, которое содержит переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.

А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.

Квадратные уравнения могут иметь два корня, один корень или не иметь корней.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b 2 − 4ac. А вот свойства дискриминанта:

если D 0, есть два различных корня.

С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.

Разобраться в теме еще быстрее с помощью опытного преподавателя можно на курсах по математике в онлайн-школе Skysmart.

Приведенные и неприведенные квадратные уравнения

Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.

Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.

Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.

Давайте-ка на примерах — вот у нас есть два уравнения:

x 2 — 2x + 6 = 0
x 2 — x — 1/4 = 0

В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x 2 ), а значит уравнение называется приведенным.

2x 2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.

Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.

Пример 1. Превратим неприведенное уравнение: 8x 2 + 20x — 9 = 0 — в приведенное.

Для этого разделим обе части исходного уравнения на старший коэффициент 8:

Ответ: равносильное данному приведенное уравнение x 2 + 2,5x — 1,125 = 0.

Полные и неполные квадратные уравнения

В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax 2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.

Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.

Неполное квадратное уравнение —— это квадратное уравнение вида ax 2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.

Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.

Для самых любопытных объясняем откуда появились такие названия:

Если b = 0, то квадратное уравнение принимает вид ax 2 + 0x+c=0 и оно равносильно ax 2 + c = 0.
Если c = 0, то квадратное уравнение выглядит так ax 2 + bx + 0 = 0, иначе его можно написать как ax 2 + bx = 0.
Если b = 0 и c = 0, то квадратное уравнение выглядит так ax 2 = 0.

Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

ax 2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
ax 2 + c = 0, при b = 0;
ax 2 + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax 2 = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0.

Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0.

Пример 1. Решить −6x 2 = 0.

Замечаем, что данному уравнению равносильно x 2 = 0, значит исходное уравнение имеет единственный корень — нуль.
По шагам решение выглядит так:

Как решить уравнение ax 2 + с = 0

Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:

перенесем c в правую часть: ax 2 = — c,
разделим обе части на a: x 2 = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней.

Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению х 2 = -c/a, которое:

не имеет корней при — c/а 0.

В двух словах

Пример 1. Найти решение уравнения 8x 2 + 5 = 0.

Разделим обе части на 8:

В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8x 2 + 5 = 0 не имеет корней.

Как решить уравнение ax 2 + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня:

Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0

Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.

Решить линейное уравнение:

0,5x = 0,125,
х = 0,125/0,5

Значит корни исходного уравнения — 0 и 0,25.

Ответ: х = 0 и х = 0,25.

Как разложить квадратное уравнение

С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:

Формула разложения квадратного трехчлена

Если x₁ и x₂ — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x₁) (x − x₂).

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b 2 − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

вычислить его значение дискриминанта по формуле D = b 2 −4ac;
если дискриминант отрицательный, зафиксировать, что действительных корней нет;
если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.

Найдем дискриминант: D = 28 2 — 4(-4)(-49) = 784 — 784 = 0
Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
Найдем корень

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6x 2 = 0.

Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x 2 — х = 0.

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x 2 — 10 = 39.

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.

D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112

Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b 2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставим в формулу корней:

2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″>

Для удобства вычислений обозначим выражение n 2 -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D₁ = n 2 — ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

вычислить D₁= n 2 — ac;
если D₁ 0, значит можно найти два действительных корня по формуле

Формула Виета

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:

Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=»215″ src=»https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE» width=»393″>

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=»52″ src=»https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG» width=»125″>

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=»52″ src=»https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo» width=»112″>

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:

Обратная теорема Виета

Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0.

Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.

Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.

2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″>

Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.

Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. А значения 4 и 2 подходят обоим равенствам:

Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p>

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12x 2 — 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 — 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 — 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

источники:

http://new-science.ru/samyj-prostoj-sposob-resheniya-kvadratichnyh-uravnenij-upuskaetsya-iz-vidu-v-techenie-4000-let/

http://skysmart.ru/articles/mathematic/kak-reshat-kvadratnye-uravneniya