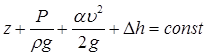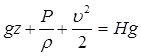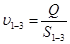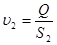Что выражает уравнение j ae

Уравнение Бернулли

Уравнение Бернулли для струйки жидкости формулируется следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Уравнение Бернулли выглядит так:

Подробное описание всех входящих в состав уравнения параметров уже описан в этой статье.

Содержание статьи

Смысл уравнения Бернулли

По существу вывода уравнение Бернулли для струйки идеальной жидкости представляет собой закон сохранения механической энергии, составленный применительно к единице массового расхода жидкости. Это следует из того, что в процессе вывода значения работы сил, приложенных к выделенному объему струйки и значения кинетической энергии этого объема были поделены на величину ρqΔT.

Отсюда вытекает, что поскольку член υ 2 /2 является мерой кинетической энергии единицы массы движущейся жидкости, то сумма членов gz+p/ρ будет мерилом ее потенциальной энергии.

В отношении величины gz это очевидно, ведь если частица жидкости массы m расположена на высоте z относительно некоторой плоскости и находится под действием сил тяжести, то способность ее совершить работу, т.е. её потенциальная энергия относительно этой плоскости равняется mgz. Но если её поделить на массу частиц m, то эта часть потенциальной энергии даст величину gz.

Для более ясного физического представления о том, что потенциальная энергия измеряется величиной p/ρ рассмотрим такую схему: пусть к трубе, заполненной жидкостью с избыточным давлением p, присоединен пьезометр, снабженный на входе в него краном.

Кран сначала закрыт, т.е. пьезометр свободен от жидкости, а элементарный объем жидкости ΔV массой ρ*ΔV перед краном находится под давлением p.

Если затем открыть кран, то жидкость в пьезометре поднимется на некоторую высоту, равную

Таким образом, единица массы, находящейся под давлением p, как бы несет в себе ещё заряд потенциальной энергии, определяемой величиной p/ρ.

В гидравлике для характеристики удельной энергии обычно используется понятие напор, под которым понимают энергию жидкости, отнесенную к единице силы тяжести, а не её массы. В соответствии с этим уравнение Бернулли записанное в начале этой статьи примет вид

Такое уравнение Бернулли для элементарной струйки идеальной жидкости в другой форме, весьма удобно для гидравлических расчетов и может быть сформулировано следующим образом.

Для элементарной струйки идеальной жидкости полный напор, т.е. сумма геометрического, пьезометрического и скоростного напоров, есть величина постоянная во всех её сечениях.

Отсюда следует, что между напором и удельной энергией существует очень простая зависимость

где э – удельная энергия

Уравнение Бернулли для элементарной струйки реальной жидкости

Если вместо идеальной жидкости рассматривать жидкость реальную, то уравнение Бернулли для реальной жидкости должно принять несколько другой вид.

При движении идеальной жидкости её полная удельная энергия или напор сохраняет постоянное значение по длине струйки, а при движении реальной жидкости эта энергия будет убывать по направлению движения. Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости.

Если же мы рассмотрим два сечения для струйки идеальной жидкости: 1-1 в начале и 2-2 в конце струйки, то полная удельная энергия будет

Полная удельная энергия для сечения 1-1 всегда будет больше, чем полная удельная энергия для сечения 2-2 на некоторую величину потерь, и уравнение Бернулли в этом случае получается

Величина Э_1-2 представляет собой меру энергии, потерянную единицей массы жидкости на преодоление сопротивлений при её движениями между указанными сечениями.

Соответствующий этой потере удельной энергии напор называют потерей напора между сечениями 1-1 и 2-2 и обозначают h_1-2 . Поэтому уравнение Бернулли для элементарной струйки реальной жидкости можно представить в виде

Уравнение Бернулли для потока реальной жидкости

Уравнение Бернулли для струйки реальной жидкости это еще только половина дела, ведь в при решении различных практических вопросов о движении жидкостей приходится иметь дело с потоками конечных размеров. Уравнение Бернулли в этом случае может быть получено, исходя из рассмотрения потока как совокупности множества элементарных струек.

Учитывая, что все струйки движутся с одной и той же средней скоростью форма записи уравнения Бернулли для потока идеальной жидкости становится идентичной его записи для элементарной струйки.

В таком виде уравнение Бернулли обычно и применяется при решении практических задач для потоков однородной несжимаемой жидкости при установившемся движении, происходящем под действием одной силы тяжести.

Такое уравнение составляется для различных живых сечений потока, вблизи которых движение жидкости должно удовлетворять условиям медленно изменяющегося движения, хотя на пути между этими сечениями движение может и не удовлетворять указанным условиям.

Слагаемое h_1-2 в этом уравнении показывает потери напора на преодоление сопротивлений движению жидкости. При этом в гидравлике различают два основных вида сопротивлений:
— h_лп — линейные потери — сопротивления, проявляющиеся по всей длине потока, обусловленные силами трения частиц жидкости друг о друга и о стенки, ограничивающие поток.
— h_мп — местные потери – местные сопротивления, обусловленные различного рода препятствиями, устанавливаемыми в потоке (задвижка, кран, колено), приводящими к изменениям величины или направления скорости течения жидкости

Поэтому полная потеря напора между двумя сечениями потока при наличии сопротивлений обоих видов будет

Видео по теме

Уравнение Бернулли подходит и для газов. Явление уменьшения давления при повышении скорости потока является основой работы различных приборов для измерения расхода. Закон Бернулли справедлив и для жидкостей вязкость которых равна нулю. При описании течения таких жидкостей используют уравнение Бернулли с добавлением слагаемых учитывающих потери на местные сопротивления.

Уравнение Бернулли

Чем выше скорость потока идеальной жидкости, тем ниже ее давление.

Вам не приходило в голову, почему самолеты весом несколько сот тонн, разогнавшись, отрываются от взлетно-посадочной полосы и устремляются ввысь? Если нет, то для начала, когда в следующий раз будете в аэропорту, внимательно приглядитесь к разрезу крыла самолета. Прежде всего, обратите внимание, что крыло в разрезе представляет собой сочетание двух выпуклых линий, причем кривизна верхнего контура больше, чем кривизна нижнего, в результате чего площадь верхней поверхности крыла больше площади его нижней поверхности. Именно эта малозаметная для непосвященных деталь конструкции и позволяет самолету отрываться от поверхности земли.

А основополагающая идея здесь такова: воздушный поток разрезается надвое передней кромкой крыла, и часть его обтекает крыло вдоль верхней поверхности, а вторая часть — вдоль нижней. Чтобы двум потокам сомкнуться за задней кромкой крыла, не образуя вакуума, воздух, обтекающий верхнюю поверхность крыла, должен двигаться быстрее относительно самолета, чем воздух, обтекающий нижнюю поверхность, поскольку ему нужно преодолеть большее расстояние. И тут в действие вступает эффект, открытый Даниилом Бернулли, одним из представителей настоящей потомственной династии неутомимых научных гениев родом из Швейцарии. (В авторитетном «Словаре научных биографий», Dictionary of Scientific Biography, упомянуто не меньше восьми представителей фамилии Бернулли.). Отец Даниила — Иоганн Бернулли — был видным профессором математики в Университете г. Гронинген (позже Иоганн Бернулли переехал в Базель и возглавил кафедру греческого языка местного университета, однако после смерти брата вернулся в Гронинген, чтобы сменить его на посту заведующего кафедрой математики. Книга Даниила «Гидродинамика» (Hydrodynamica) была опубликована в 1738 году, практически одновременно с книгой Иоганна Бернулли «Гидравлика» (Hydraulica), которая по взаимной договоренности между сыном и отцом была, однако, специально датирована 1732 годом, чтобы, в случае чего, в семье не возникло недоразумений относительно приоритетов в открытиях. Вот такая семья!).

Объединив законы механики Ньютона с законом сохранения энергии (см. Первое начало термодинамики) и условием неразрывности жидкости, Даниил Бернулли смог вывести уравнение, согласно которому давление со стороны текучей среды падает с увеличением скорости потока этой среды (понятие «текучая среда» включает жидкость или газ). В случае с самолетом воздух обтекает крыло самолета снизу медленнее, чем сверху. И благодаря этому эффекту обратной зависимости давления от скорости давление воздуха снизу, направленное вверх, оказывается больше давления сверху, напрвленного вниз. В результате, по мере набора самолетом скорости, возрастает направленная вверх разность давлений, и на крылья самолета действует нарастающая по мере разгона подъемная сила. Как только она начинает превышать силу гравитационного притяжения самолета к земле, самолет в буквальном смысле взмывает в небо. Эта же сила удерживает самолет в горизонтальном полете: на крейсерской скорости и высоте подъемная сила уравновешивает силу тяжести.

Если вы часто летаете самолетом, вы не могли не заметить и еще одного явления, напрямую связанного с эффектом Бернулли. Самолет в аэропорту вашего родного города в разные дни берет разгон по взлетно-посадочной полосе в противоположных направлениях, и садится на нее также то в одном, то в другом направлении. Выбор направления не произволен: он зависит от направления ветра. При движении навстречу преобладающему ветру скорость воздушного потока, обтекающего крыло самолета, равна скорости самолета относительно земли плюс скорость самого ветра относительно земли. Поэтому при движении навстречу ветру, скорость отрыва от земли, при которой подъемная сила, описываемая уравнением Бернулли, начинает превышать силу тяжести, оказывается ниже, и самолету требуется меньшая длина разбега или торможения после посадки. Тем самым снижается риск выхода за пределы взлетно-посадочной полосы и экономится горючее за счет того, что часть подъемной силы создается за счет энергии встречного ветра.

С эффектом Бернулли вы можете встретиться также, когда сидите ненастным вечером дома у камина. Во время особенно сильных порывов ветра языки пламени взмывают вверх, в дымоход. А происходит следующее: когда скорость ветра у выходного отверстия трубы возрастает, давление в этом месте падает. Более высокое давление внутри дома буквально «выталкивает» пламя из камина в дымоход. Вы, наверное, замечали спиральные лопатки вокруг выходных отверстий заводских труб. Они установлены там с той же целью: направляя ветер вокруг и над отверстием трубы, они способствуют белее эффективному выбросу отработанных газов.

Сам я использую эффект Бернулли весьма неожиданным образом. Для поддержания физической формы я у себя в Вашингтоне регулярно совершаю пробежки на роликовых коньках по специальной заасфальтированной дорожке, идущей вдоль реки Потомак. На трек я выхожу неподалеку от Национального аэропорта, и, еще паркуя свою машину, я первым делом смотрю, в каком направлении взлетают или приземляются авиалайнеры. Если они садятся или взлетают в том направлении, куда я собираюсь прокатиться, значит, всё в порядке, и на обратном пути мне будет помогать попутный ветер. Если же они садятся мне навстречу, значит, дистанцию пробежки лучше сократить, поскольку на обратном пути ветер будет дуть мне в лицо, а я этого не люблю. Тем самым эффект Бернулли позволяет мне точно дозировать ежедневные физические нагрузки.

Швейцарский математик, физик и физиолог. Родился в Гронингене (Нидерланды) в семье потомственных математиков и интеллектуалов. Первоначально получил медицинское образование, и в 1725 году принял приглашение Петербургской академии наук и занял пост профессора кафедры физиологии. Обнаружив в этой области множество нерешенных задач из области теоретической физики и, в частности, динамики движения жидкости (крови) в сосудах, вернулся к математическому описанию физических процессов и в 1730 году возглавил кафедру чистой математики Петербургской академии. В 1733 году вернулся на родину в Базель, где возглавил кафедру анатомии и ботаники местного университета, а с 1750 года — кафедру экспериментальной физики, которой и руководил до своей смерти. В результате изучения гидродинамических зависимостей сформулировал так называемый принцип Бернулли и на столетие предвосхитил зарождение молекулярно-кинетической теории газов.

Энергетический смысл уравнения Бернулли

Определения

Элементарная струйка – струйка жидкости, боковая поверхность которой образована линией тока, проходящей через бесконечно малый замкнутый контур. Распределение скоростей по поперечному сечению элементарной струйки считается равномерным, по причине малости площади поперечного сечения, поэтому коэффициент Кориолиса 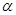равен единице.

Идеальная жидкость – модель жидкости, применяемая для расчётов реальных гидродинамических процессов.

Для идеальной жидкости приняты следующие допущения:

· отсутствуют касательные напряжения между слоями жидкости, следовательно,

отсутствует вязкость жидкости, следовательно, отсутствует трение между слоями жидкости, следовательно, в жидкости отсутствуют потери напора;

· жидкость является не сжимаемой;

· в жидкости отсутствует теплопроводность, т.е. жидкость не изменяет свой объём при изменении температуры;

· поток жидкости является сплошным, т.е. в жидкости отсутствуют места пустот или переуплотнений.

Виды уравнения Бернулли

Для элементарной струйки идеальной жидкости

Для элементарной струйки коэффициент Кориолиса равен единице, в идеальной жидкости отсутствуют потери, поэтому уравнение Бернулли будет иметь вид:

(1)

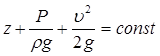
Для потока реальной жидкости

Для потока жидкости коэффициент Кориолиса будет иметь значение отличное от единицы, и зависеть от режима течения, для ламинарного режима α = 2, для турбулентного режима α = 1,05-1,1. Реальная жидкость имеет вязкость, следовательно, в реальной жидкости будут потери напора, поэтому уравнение Бернулли будет иметь вид:

Геометрический смысл уравнения Бернулли

Рассмотрим уравнение Бернулли для элементарной струйки идеальной жидкости (1).

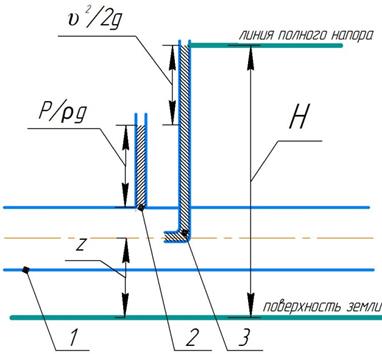
В уравнении (1) все три слагаемых имеют линейную размерность [м]. Соответственно каждую высоту можно представить в виде реальных отрезков:

геометрическая высота, представляет собой расстояние от оси элементарной струйки (трубопровода) до поверхности земли.

пьезометрическая высота, показывает на какую высоту, может подняться жидкость под действием избыточного давления в данной точке, при условии, что на свободную поверхность действует давление внешней газообразной среды (т.е. атмосферное давление).

скоростная высота, показывает высоту, при падении с которой, частица жидкости достигла бы скорости .

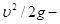
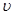
Рис. 1 Иллюстрация геометрического смысла уравнения Бернулли.

1 – элементарная струйка; 2 – пьезометр; 3 – трубка Пито (прибор для измерения скоростной высоты).

Геометрический смысл уравнения Бернулли заключается в следующем: по длине элементарной струйки сумма трёх слагаемых уравнения Бернулли остаётся величиной постоянной и равной величине полного напора Н [м].

(2)

Энергетический смысл уравнения Бернулли

Умножим каждое слагаемое уравнения (2) на величину ускорения свободного падения:

В итоге получаем слагаемые, который можно описать с точки зрения энергии:

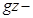
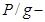
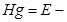
где удельная потенциальная энергия положения, т.е. если поднять жидкость массой 1 кг на высоту , то она будет иметь потенциальную энергию ;

удельная потенциальная энергия давления;

удельная кинетическая энергия;

полная удельная механическая энергия элементарной струйки.

Энергетический смысл уравнения Бернулли заключается в следующем: по длине элементарной струйки сумма трёх удельных энергий остаётся величиной постоянной и равной величине полной удельной механической энергии Е [Дж]. Возможна и другая формулировка: уравнение Бернулли – это есть закон сохранения энергии для элементарной струйки (потока) жидкости, который отображает взаимный переход кинетической и потенциальной энергии.

Потери

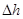
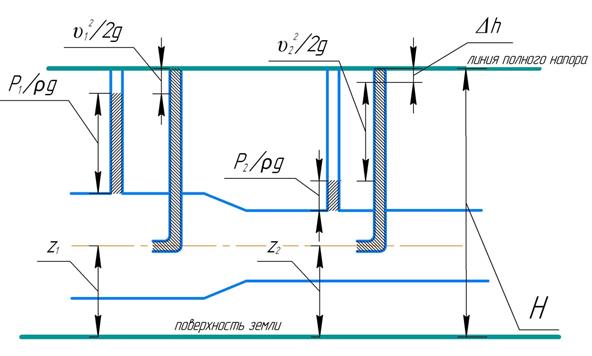
В потоке реальной жидкости в уравнение Бернулли добавляется слагаемое , которое

представляет собой величину потерь напора. Запишем уравнение Бернулли для двух произвольных сечений потока жидкости:

С геометрической точки зрения потери отображаются отрезком, расположенным над скоростным напором, при этом потери отображаются во втором сечении.

Рис. 2. Иллюстрация потерь напора.

С энергетической точки зрения 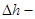это величина, показывающая, сколько энергии жидкость тратит на преодоление различных сопротивлений при переходе из первого сечения во второе сечение.

6. Порядок проведения расчётов:

1. Определить величину расхода жидкости:

2. Поскольку диаметры d₁=d₃, дальнейшие расчёты для широких частей трубопровода будут одинаковы. Поэтому будем проводить расчёт для одной широкой части трубопровода, при этом параметры жидкости, обозначая через индекс _1-3

Определить площади поперечного сечения трубопроводов S_1-3, S₂ [м];

3. Определить скорость течения жидкости:

4. Определить режим течения жидкости:

5. Определить величины скоростного напора: ;

6. На листе А4 построить график, зависимости изменения пьезометрического напора от

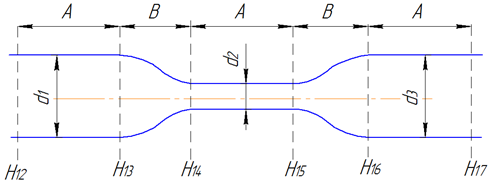
длины сечения трубопровода.По оси Х откладываются расстояния между точками, к которым подключены пьезометры. Расстояния равны: А=25см, В=12,5 см

Рис. 3 Условное изображение исследуемого

трубопровода с точками подключения пьезометров.

По оси Y откладываются показания соответствующих пьезометров. В результате получится шесть точек, который соединяются ломаной линией. Поскольку экспериментальные исследования проводились для трёх различных случаев, поэтому в результате мы имеем три графика в одной системе координат.

7. На листе А4 построить график, зависимость изменения скоростного напора от длины

сечения трубопровода.По оси Х откладывается расстояние между точками, к которым подключены пьезометры. Расстояния равны: А=25см, В=12,5 см.

По оси Y откладываются значения скоростного напора. Поскольку экспериментальные исследования проводились для трёх различных случаев, поэтому в результате мы имеем три графика в одной системе координат.

8. Вывод о работе с описанием графиков

Таблица 1. Результаты опыта