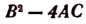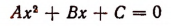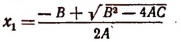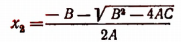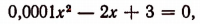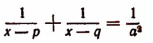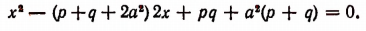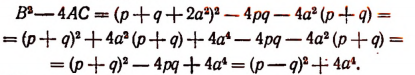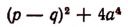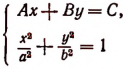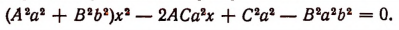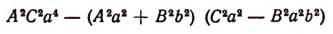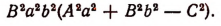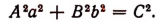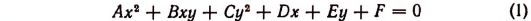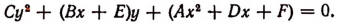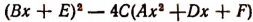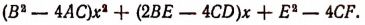Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность. Первая часть.
Исследовать систему линейных агебраических уравнений (СЛАУ) на совместность означает выяснить, есть у этой системы решения, или же их нет. Ну и если решения есть, то указать сколько их.
Нам понадобятся сведения из темы «Система линейных алгебраических уравнений. Основные термины. Матричная форма записи». В частности, нужны такие понятия, как матрица системы и расширенная матрица системы, поскольку именно на них опирается формулировка теоремы Кронекера-Капелли. Как обычно, матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $\widetilde$.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. $\rang A=\rang\widetilde$.
Следствие из теоремы Кронекера-Капелли
Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения или нет, а если существуют – то сколько.
Исследовать СЛАУ $ \left \ <\begin
Чтобы выяснить наличие решений заданной СЛАУ, используем теорему Кронекера-Капелли. Нам понадобятся матрица системы $A$ и расширенная матрица системы $\widetilde$, запишем их:
Способ №1. Вычисление рангов по определению.
Согласно определению, ранг – это наивысший порядок миноров матрицы, среди которых есть хоть один, отличный от нуля. Обычно исследование начинают с миноров первого порядка, но здесь удобнее приступить сразу к вычислению минора третьего порядка матрицы $A$. Элементы минора третьего порядка находятся на пересечении трёх строк и трёх столбцов рассматриваемой матрицы. Так как матрица $A$ содержит всего 3 строки и 3 столбца, то минор третьего порядка матрицы $A$ – это определитель матрицы $A$, т.е. $\Delta A$. Для вычисления определителя применим формулу №2 из темы «Формулы для вычисления определителей второго и третьего порядков»:
$$ \Delta A=\left| \begin
Итак, есть минор третьего порядка матрицы $A$, который не равен нулю. Минор четвёртого порядка составить невозможно, так как для него требуется 4 строки и 4 столбца, а в матрице $A$ всего 3 строки и 3 столбца. Итак, наивысший порядок миноров матрицы $A$, среди которых есть хотя бы один не равный нулю, равен 3. Следовательно, $\rang A=3$.
Задача решена. Какие недостатки и преимущества имеет данный способ? Для начала поговорим о плюсах. Во-первых, нам понадобилось найти всего один определитель. После этого мы сразу сделали вывод о количестве решений. Обычно в стандартных типовых расчётах даются системы уравнений, которые содержат три неизвестных и имеют единственное решение. Для таких систем данный метод очень даже удобен, ибо мы заранее знаем, что решение есть (иначе примера не было бы в типовом расчёте). Т.е. нам остаётся только показать наличие решения наиболее быстрым способом. Во-вторых, вычисленное значение определителя матрицы системы (т.е. $\Delta A$) пригодится после: когда станем решать заданную систему методом Крамера или с помощью обратной матрицы.
Однако метод вычисления ранга по определению нежелательно применять, если матрица системы $A$ является прямоугольной. В этом случае лучше применить второй метод, о котором пойдёт речь ниже. Кроме того, если $\Delta A=0$, то мы ничего не сможем сказать о количестве решений заданной неоднородной СЛАУ. Может, СЛАУ имеет бесконечное количество решений, а может – ни одного. Если $\Delta A=0$, то требуется дополнительное исследование, которое зачастую является громоздким.
Подводя итог сказанному, отмечу, что первый способ хорош для тех СЛАУ, у которых матрица системы квадратна. При этом сама СЛАУ содержит три или четыре неизвестных и взята из стандартных типовых расчетов или контрольных работ.
Способ №2. Вычисление ранга методом элементарных преобразований.
Какие преимущества второго способа? Главное преимущество – это его универсальность. Нам совершенно неважно, является ли матрица системы квадратной или нет. Кроме того, мы фактически провели преобразования прямого хода метода Гаусса. Осталось лишь пару действий, и мы смогли бы получить решение данной СЛАУ. Честно говоря, второй способ нравится мне более первого, но выбор – это дело вкуса.
Ответ: Заданная СЛАУ совместна и определена.
$$ \left( \begin
Расширенная матрица системы приведена к ступенчатому виду. Ранг ступенчатой матрицы равен количеству её ненулевых строк, поэтому $\rang\widetilde=3$. Матрица $A$ (до черты) тоже приведена к ступенчатому виду, и ранг её равен 2, $\rang=2$.
Ответ: система несовместна.
Приводим расширенную матрицу системы к ступенчатому виду:
$$ \left( \begin
Мы привели расширенную матрицу системы и саму матрицу системы к ступенчатому виду. Ранг расширенной матрицы системы равен трём, ранг матрицы системы также равен трём. Так как система содержит $n=5$ неизвестных, т.е. $\rang\widetilde=\rang\lt
Ответ: система является неопределённой.
Во второй части мы разберём примеры, которые нередко включают в типовые расчёты или контрольные работы по высшей математике: исследование на совместность и решение СЛАУ в зависимости от значений параметров, входящих в неё.
Исследование уравнений в математике с примерами решения
Исследовать уравнение – это значит указать, при каких значениях параметра какое именно решение имеет данное уравнение/неравенство.
Что значит исследовать уравнение
Исследовать уравнение — значит рассмотреть все особые случаи, которые могут представиться при решении его, и уяснить значение этих случаев для той задачи, из условий которой уравнение составлено.
Исследование уравнений первой степени с одним неизвестным
Вы видели раньше, что уравнение первой степени с одним неизвестным после надлежащих преобразований (раскрытие скобок, освобождение от знаменателей, перенесение неизвестных членов в одну часть уравнения, а известных в другую и приведение подобных членов) приводится к такому простейшему виду:
ах = b,
где числа а и b могут быть положительными, отрицательными и равными нулю.
Рассмотрим, какого рода решения получает это уравнение при различных численных значениях а и b .
Положительное решение: Такое решение получается тогда, когда числа а и b оба положительны или оба отрицательны. Пусть, например, Зх = 6 или —Зх = —6. Тогда мы получим:
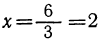
Положительное решение, удовлетворяя уравнению, вместе с тем удовлетворяет и задаче, из условий которой уравнение выведено, если только в уравнении выражены все условия задачи. Но иногда случается, что не все условия задачи выражены уравнением; тогда положительное решение может и не удовлетворять задаче. Приведём этому пример.
Задача:
Рабочий кружок, состоящий из 20 человек (взрослых и подростков), устроил сбор на покупку книг для библиотеки, причём каждый взрослый внёс по 3 руб., а каждый подросток—по 1 руб. Сколько было в этом кружке взрослых и сколько подростков, если весь сбор составил 35 руб.?
Обозначим число взрослых буквой х; тогда число подростков будет 20 — х, и сбор со взрослых окажется Зх руб., а с подростков (20 — х) руб. Следовательно, уравнение будет
3x+(20 — x)=35, откуда х =
Это положительное решение удовлетворяет уравнению, но не удовлетворяет задаче, так как по смыслу задачи искомое число должно быть целым. Различие между уравнением и задачей произошло здесь оттого, что уравнение не содержит в себе подразумеваемого в задаче требования, чтобы искомое число было целым. Предложенная задача не имеет решений.
Отрицательное решение: Такое решение получается из уравнения ax=b тогда, когда числа а и b имеют противоположные знаки. Пусть, например,
5х = — 15 или —5x=15;
тогда:
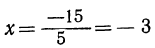
Чтобы показать, в каком смысле надо понимать отрицательное решение x=—m, обратим внимание на то, что если число —m удовлетворяет данному уравнению αx=b, то равенство —am = b должно быть тождеством; значит, тогда положительное число m удовлетворяет другому уравнению: — ax=b, которое получается из данного, если в нём заменим х на — х. Основываясь на этом замечании и получив отрицательное решение х=— m, мы можем поступить так: изменим в уравнении х на — х; от этого получим новое уравнение, которое должно иметь положительное решение х=m. Новое уравнение, конечно, не соответствует предложенной задаче; всматриваясь в него, мы легко определим, как надо изменить задачу, чтобы она имела положительное решение х=m.
Для примера приведём такую простую задачу.
Отцу 40 лет, а сыну 10 лет. Через сколько лет отец будет в 7 раз старше сына?
Обозначим искомое число буквой х.
Очевидно, что через х лет отцу будет 40+х, а сыну 10+x лет. По условию:
40+x=7 (10+x), откуда x=— 5.
Заменив в уравнении х на — х, получим новое уравнение 40 — x = 7 (10 — х), которое отвечает той же задаче, но с изменённым вопросом, а именно, вопрос должен быть такой: сколько лет назад отец был в 7 раз старше сына?
Из примеров, подобных указанному, можно усмотреть, что отрицательное решение надо понимать в смысле, противоположном тому, в каком понималось бы положительное решение; так, если положи тельное решение означает время после некоторого события, то отрицательное означает время раньше этого события; если первое означает доход, то второе — расход и т. п. Если же случается, что по смыслу задачи неизвестное число х нельзя понимать в двух противоположных смыслах, то тогда отрицательное решение означает, что задача не имеет решения.
Нулевое решение: Положим, что в уравнении ах=b число b окажется нулём, а коэффициент а будет какое-нибудь число, отличное от нуля. Пусть, например, уравнение будет 4х=0. Значит, произведение 4х должно равняться нулю. Но произведение равняется нулю только тогда, когда какой-нибудь сомножитель равен нулю; следовательно, сомножитель х должен равняться нулю. И из формулы 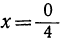
Задача:
Какое число надо прибавить к числителю и знаменателю дроби 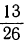
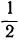
Обозначив искомое число буквой х, мы получим уравнение:
откуда:
26+2x=26+x; х=0.
Это значит, что дробь сама равна 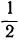
Случай, когда уравнение не имеет корня
Пусть в уравнении ax=b число а окажется нулём, а число b не равно нулю; например, 0∙x = 10. Такое равенство невозможно, так как, какое бы число мы ни взяли для х, произведение 0∙x равно нулю, а не 10.
Пусть, например, уравнение будет такое:
Решаем его, как обыкновенно (общий знаменатель 6):
Зх — 24+2x = 42+5x,
т. е.
5x = 66+5x, или 5х — 5x=66.
Какое бы число х мы ни взяли, разность 5х — 5х всегда равна нулю, а не числу 66. Значит, предложенное уравнение не имеет корня.
Если бы мы, не заметив, что коэффициент а равен нулю, разделили па него обе части уравнения ax=b, то получили бы для х такую формулу: 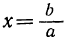
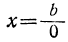
Так как деление на 0 невозможно, то из последней формулы мы пришли бы к заключению, что при α=0 уравнение ax = b не имеет корня (значит, и задача не имеет решений).
Но недостаточно ограничиться только этим одним заключением. Полезно указать ещё на одно важное обстоятельство, для уяснения которого мы предварительно должны рассмотреть, как изменяется дробь, когда знаменатель её неограниченно уменьшается, а числитель, остаётся неизменным.
Как надо понимать равенство 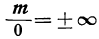
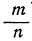
Положим, например, что знаменатель n получает такие уменьшающиеся значения:
n = 0,l; n = 0,01; n = 0,001; n = 0,0001 и т. д.
Тогда дробь будет получать такие возрастающие значения:
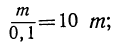
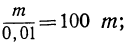
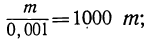
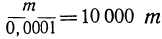
Отсюда видно, что если числитель остаётся неизменным, а знаменатель неограниченно приближается к нулю, то абсолютная величина дроби 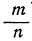
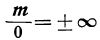
где знак ∞ выражает „бесконечность». Запись эту нельзя понимать буквально, так как деление на 0 невозможно; она только кратко означает, что абсолютная величина дроби неограниченно увеличивается (или, как иногда говорят, стремится к бесконечности), если знаменатель неограниченно приближается к нулю, а числитель остаётся неизменным, причём сама дробь остаётся или положительной, или отрицательной (смотря по тому, имеет ли знаменатель, стремящийся к нулю, одинаковый знак с числителем или противоположный).
Теперь мы можем дополнить исследования так:
При а = 0 уравнение ах = b не имеет корня, но если а не равно 0, а только приближается к 0 всё ближе и ближе, то абсолютная величина корня возрастает неограниченно.
Неопределённое решение: Если в уравнении ax=b оба числа а и b окажутся нулями, то уравнение обращается в тождество: 0∙x = 0, верное при всяком значении х. Значит, в этом случае уравнение становится неопределённым, т. е. оно допускает бесчисленное множество произвольных решений.
Если бы мы, не заметив, что α = 0, разделили обе части уравнения на а, то для х получили бы дробь 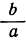
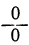
Задача:
Какое число надо прибавить к числителю и знаменателю дроби у, чтобы эта дробь сделалась равной числу m?
Обозначив искомое число буквой х, получим такое уравнение: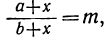
откуда:
a+x=bm+mx; х — mx=bm- a; (1-m)x = bm-a.
Если m≠l, то
Допустим, что m=1, а разность b — а есть какое-нибудь число, отличное от нуля (положительное или отрицательное). Тогда для х получим:
0∙x=b — а.
Отсюда мы можем заключить, что при m = 1 и b ≠ а не существует никакого числа х, удовлетворяющего вопросу задачи, но если m не равно 1, а только приближается к 1, то абсолютная величина числа х увеличивается неограниченно.
Если же при m=l ещё b=a, то для х получается формула:
0∙x=0,
из которой можно заключить, что всякое число х удовлетворяет вопросу задачи (и действительно: дробь 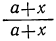
Графическое истолкование решения уравнения ax=b:
Обозначим левую часть уравнения буквой y₁ и правую часть — буквой y₂ и построим на одном и том же чертеже графики двух функций: y₁ =ax и y₂=b.
График первой функции есть прямая, проходящая через начало координат и через точку (1, а); график второй функции есть прямая, параллельная оси х-ов и отсекающая от оси у-ов отрезок ¢ ‘(на чертеже 31 мы изобразили случай, когда а>0 и b>0; предоставляем самим читателям сделать чертежи для случаев, когда 1) α>0, но 0 и 3) α 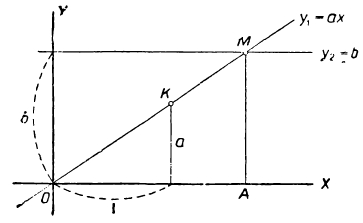
Пользуясь таким графическим изображением, мы можем наглядна
истолковать все случаи решения уравнения ax = b. Ограничимся рассмотрением двух случаев: 1) уравнение не имеет решения и 2)уравнение имеет неопределённое решение.
1) Уравнение не имеет решений (черт. 32). Уменьшая численную величину коэффициента а, мы заставляем прямую у=ах всё более и более приближаться к оси х-ов. Тогда точка M, в которой прямая у=b пересекается с прямой y=αx, всё более и более удаляется направо, проходя через положения M₁, M₂, M₃ и т. д., причём абсцисса OA точки пересечения беспредельно увеличивается, принимая значения OA₁, OA₂ , OA₃ и т. д. Значит, когда а неограниченна уменьшается, приближаясь к нулю, корень уравнения ax = b неограниченно возрастает (что можно выразить так: 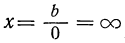
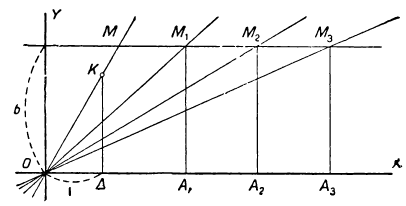
2) Неопределённое решение получается, как мы видели, при a = b=0. Чтобы истолковать этот случай графически, вообразим, что на чертеже 32 величина b уменьшается, приближаясь к нулю; тогда прямая y₂=b, оставаясь параллельной оси х-ов, будет всё более и более приближаться к этой оси и при b=0 сольётся с нею. C другой стороны, прямая y₁ = ax при а=0 обратится тоже в ось х-ов, и тогда две прямые y₂ =b и y₁=ax совпадут с осью х-ов, и, следовательно, каждую из точек этой оси можно считать за точку пересечения; значит, величина корня остаётся неопределённой.
Исследование системы двух уравнений первой степени с двумя неизвестными
Общие формулы: Мы видели что система двух уравнений:
ax+by=с и a’x+b’y=c’
даёт следующие формулы для неизвестных:
(ab’— a’b)x=(b’c — bс’); (ab’ — a’b) y=(ac’ — а’с). (1)
Если ab’ — a’b≠0, то
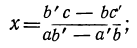
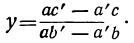
Исследование: Исследование этих формул подразделим на два случая:
1) Общий знаменатель ab’ — а’b не равен нулю.
В этом случае система имеет единственное решение. О значении этого решения для задачи, из условий которой составлена рассматриваемая система, здесь может быть сказано то же самое, что говорилось раньше при исследовании одного уравнения с одним неизвестным.
2) Общий знаменатель ab’— a’b=0. В этом случае числители в формулах (2) могут быть как отличными от нуля, так и равными нулю. Докажем, что если ни одно из чисел a, a’, b, b’ не равно нулю, то будет иметь место одно из следующих двух предположений.
а) Если один из числителей для х или для у в формулах (2) равен дулю, то и другой равен нулю.
Пусть, например, числитель для х равен нулю, для чего необходимо, чтобы:
cb’=c’b; и, кроме того, дано, что ab’=a’b.
Умножив левую часть первого из этих равенств на правую часть второго, а правую — на левую второго, получим:
cb’a’b=c’bab’, откуда cb’a’b — c,bab, =0,
и, следовательно,
bb’ (а’с — ac’)=0.
Так как числа b и b’ не равны нулю, то последнее равенство возможно только тогда, когда а’с — ac’=0, т. е. числитель для у равен нулю.
Так же, если допустим, что числитель для у в формулах (2) равен нулю (т. е. если ac’ = a’c и ab’=a’b), то получим:
ас’a’b=a’cab’ ; aa’ (c’b — cb’)=0; c’b — cb’=0.
б) Если один из числителей для х или для у в формулах (2) не равен нулю, то и числитель для другого неизвестного также не равен нулю.
Действительно, если бы для одного из неизвестных числитель был бы равен нулю, то, по доказанному, числитель для другого неизвестного также был бы равен нулю.
Если числители для обоих неизвестных в формулах (2) равны нулю, то это означает неопределённость задачи. Действительно, умножив все члены первого уравнения на b’, а члены второго на b (что можно сделать, так как, по предположению, числа b и b’ не равны 0), получим:
ab’x+bb’y=cb’ и a’bx+b’by=c’b. [А]
Но ab’ = a’b и cb’ =c’b; следовательно, оба уравнения [А] представляют собой в сущности одно уравнение с двумя неизвестными, а в этом случае, как мы знаем, неизвестные могут иметь бесчисленное множество значений.
Если числители в формулах (2) не равны нулю, a ab’ — a’b=0, то это означает несовместимость уравнений. В самом деле, если ab’ = a’b , a cb’ ≠ c’b , то левые части системы [А] имеют одинаковые численные величины, а правые — разные; значит, уравнения несовместимы, и задача не имеет решения.
Полезно заметить, что в случае, когда уравнения (1) принимают вид 0x=0, 0y=0, то это ещё не значит, что обоим неизвестным можно давать произвольные значения. Выбрав значения одного из них произвольно, мы тем самым определим другое неизвестное, найдя его из какого-нибудь одного из двух данных уравнений.
Итак, если ab’—a’b≠0, то решение системы:
ax+by=c, a’x+b’y=c’
получается по общим формулам; если же ab’ — a’b=0, но ни одно из чисел a, b, a’, b’ не обращается в нуль, то система или имеет бесчисленное множество решений, или ни одного решения. Случай, когда ab’—a’b=0 и, кроме того, какое-либо из чисел a, b, a’, b’ равно нулю, мы не рассматриваем.
Исследование квадратного уравнения
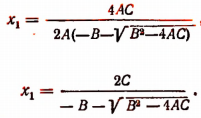
Исследование формул: Корни полного квадратного уравнения αx²+bx+c=0 выражаются, как мы знаем, формулами:
Число а мы будем считать положительным (если бы оно было отрицательное, мы могли бы переменить знаки перед всеми членами уравнения на противоположные; нулём число а быть не может, так как в противном случае уравнение перестало бы быть квадратным, оно обратилось бы в уравнение первой степени).
Мы говорили ранее, что корни квадратного уравнения будут оба вещественные или оба мнимые в зависимости от того, окажется ли дискриминант b² — 4ас величиной положительной или отрицательной.
Рассмотрим этот вопрос подробнее: 1) Если b² — 4ас > 0 , то 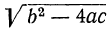
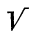
а) Оба корня — положительные числа, если 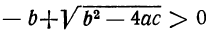
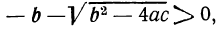
б) Оба корня — отрицательные числа, если 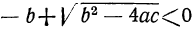
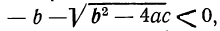
в) Один корень — положительный, а другой — отрицательный, когда b, будучи положительным или отрицательным, по абсолютной величине меньше 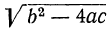
2) Если b² —4αc=0, то корни будут вещественные и равные: 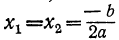
3) Если b² —4αc 
Подобно этому найдём, что точка С, отстоя от источника света В на (d— х) м, будет иметь освещённость от В в 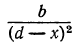
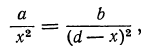
откуда:
a(d — x)²=bx², т. е. ad² — 2αdx+αx²— bx2=0,
(α — b)x² — 2adx+ad²=0.
Так как коэффициент при х делится на 2, то
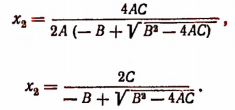
Следовательно,
Исследуем эти формулы. Так как а и b — числа положительные, то мнимых решений в этой задаче не будет.
1) Если a>b, то оба корня положительны, причём, так как
Второе решение (x₂ d) ему противоречит. Чтобы принять или отвергнуть это решение, мы должны рассмотреть, какое уравнение получится, если сделаем предположение, что искомая точка находится направо от В (например, в C₁) на расстоянии х от А. Тогда по-прежнему освещённость её источником А будет 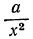
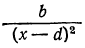
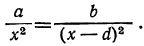
Сравнивая это уравнение с уравнением (1), находим, что они одинаковы, так как
(d-x)²=(x-d)²∙
Заметив это, мы можем утверждать, что оба положительные решения уравнения (1) удовлетворяют задаче.
2) Если a Исследование уравнений
Исследовать уравнение — значит определить, имеет ли данное уравнение решения и, если имеет, то сколько.
Кроме этого основного вопроса, в исследование уравнения может входить необходимость выяснения и других частных вопросов. Например, вопроса о числе действительных, отрицательных, рациональных и целых корней.
Решение всех этих вопросов порой представляет большие трудности и не может быть достигнуто средствами только элементарной алгебры. Эти вопросы более подробно рассматриваются в курсах высшей алгебры. Элементарная же алгебра ими занимается частично.
Исследование уравнения первой степени с одним неизвестным
Общий вид уравнения 1-й степени с одним неизвестным таков:
1. Если 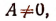
Если А и В — числа действительные, то и решение действительное.
Если А и В — мнимые, то решение может оказаться мнимым, но может оказаться и действительным.
Если А и В — действительные числа, одновременно положительные или одновременно отрицательные, то решение уравнения будет отрицательным.
Если А и В — действительные числа, из которых одно положительное, а другое отрицательное, то решение уравнения будет положительным.
Если В = 0, то единственным решением уравнения будет х = 0.
Если А=О и 
Если А = 0 и В = 0, то решением уравнения будет являться любое число. Уравнение будет иметь бесконечное множество решений.
Пусть требуется исследовать уравнение
После преобразований данное уравнение примет вид:
1. Если 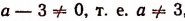
Это единственное решение окажется равным нулю лишь тогда, когда а = 5.
Если а — 3 = 0, т. е. а = 3, то уравнение примет вид:
Следовательно, при а = 3 данное уравнение не будет иметь ни одного решения.
Данное уравнение никогда не может иметь более одного решения, так как выражения (а — 3) (а — 5) не могут одновременно обратиться в нуль.
В исследование данного уравнения могут войти и другие вопросы. Например, поставим такой вопрос. «При каких значениях буквы а решение данного уравнения будет числом положительным?»
Для ответа на этот вопрос надо решить неравенство
Решив это неравенство, найдем, что корень данного уравнения будет положительным только тогда, когда
3
Исследование этого уравнения предлагается учащемуся сделать самостоятельно. Ниже приводится результат этого исследования.
- При а, равном 2, уравнение не имеет ни одного корня.
- При а, равном 3, любое число будет корнем данного уравнения.
- При всех прочих значениях а данное уравнение имеет только одни корень.
Исследование системы двух уравнений 1-й степени с двумя неизвестными
Общий вид системы двух уравнений 1-й степени о двумя неизвестными таков:
Умножим сначала обе части первого уравнения на 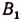
Теперь умножим обе части первого уравнения на 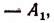
1. Если 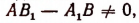
2. Если 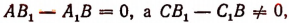
Также система не будет иметь ни одного решения, если окажется, что
3. Если 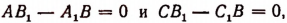
будет иметь своим решением любое число. Чтобы в этом случае находить решения системы, достаточно в одно из данных уравнений, например в уравнение
подставлять вместо буквы х любое число и после этого находить значение неизвестного у, соответствующее выбранному значению х. В этом случае данная система будет иметь бесконечное множество решений. Однако решением системы не может быть, вообще говоря, любая пара чисел, а лишь пара чисел, надлежащим образом найденная.
Если окажется 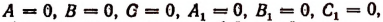
Результаты произведенного исследования системы (I) можно оформить еще и так:
1) Если 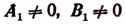
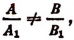
2) Если 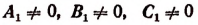
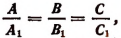
3) Если 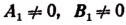
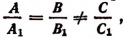
называется, как нам уже известно (см. стр. 217), определителем системы (I).
Примеры:
Следовательно, эта система имеет одно и только одно решение.
2. Определитель системы:
Следовательно, эта система не имеет ни одного решения.
3. Определитель системы:
Следовательно, эта система имеет бесконечное множество решений.
Для получения решений этой системы достаточно одной из неизвестных, например х, давать любое значение и каждый раз находить из уравнения х + у = 10 соответствующее значение неизвестного у.
Таким образом, можем получить сколько угодно решений этой системы:
Исследование квадратного уравнения
Общий вид квадратного уравнения таков:
- Если
то уравнение имеет два действительных различных корня.
- Если
то уравнение имеет два действительных одинаковых корня.
- Если
то уравнение имеет два мнимых сопряженных корня.
называется дискриминантом квадратного уравнения.
В исследование квадратного уравнения могут входить и другие вопросы. Например, исследуем характер корней уравнения
при условии, что
При
При
Таким образом, получилось следующее:
Если 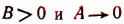
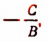
Можно убедиться, что получится такой же результат при 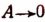
убедитесь в том, что один из корней будет близок к числу 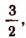
В заключение рассмотрим еще следующий пример. Может ли уравнение
иметь мнимые корни, если все числа р, q и а действительные? Преобразовав данное уравнение, получим:
Дискриминант этого уравнения
ни при каких действительных значениях р, q и а не может быть числом отрицательным. Следовательно, данное уравнение не может иметь мнимых корней.
Примеры решения уравнений
1. Найти условия, при которых система
имеет два действительных решения, два мнимых сопряженных решения и, наконец, одно решение (двукратное).
Определив у в зависимости от х из первого уравнения и подставив во второе, получим после преобразований:
Дискриминант этого квадратного уравнения
после преобразований принимает вид:
Следовательно, данная система имеет два различных действительных решения, если 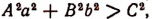
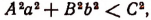
2. Вывести условие, при котором у выражается из уравнения
рационально в зависимости от х.
Преобразуем данное уравнение к форме квадратного уравнения относительно неизвестного у:
Дискриминант этого уравнения
после преобразований примет вид:
Для того чтобы у выразился в зависимости от х, рационально, необходимо и достаточно, чтобы последний трехчлен 2-й степени относительно х оказался полным квадратом, т. е. чтобы его дискриминант равнялся нулю (см. стр. 300).
является необходимым и достаточным условием того, чтобы из уравнения (1) у выражался в зависимости от х рационально.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Исследование СЛАУ. Общие сведения
В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.
Общие сведения (определения, условия, методы, виды)
Системы линейных алгебраических уравнений с n неизвестными могут иметь:
- единственное решение;
- бесконечное множество решение (неопределенные СЛАУ);
- ни одного решения (несовместные СЛАУ).
Пример 1
Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.
Система x + y = 1 2 x + 7 y = — 3 имеет единственное решение x = 2 ; y = 1 .
Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 — t при — ∞ t ∞ .
Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:
- Совместна ли система?
- Если система совместна, то, какое количество решений она имеет — одно или несколько?
- Как найти все решения?
Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:
- если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
- если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
- если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.
Ранг матрицы и его свойства
Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.
Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда
В математике выделяют следующие подходы к определению ранга матрицы:
- при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
- при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
- при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.
Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .
Свойства ранга матрицы:
- квадратная невырожденная матрица обладает рангом, который отличается от нуля;
- если транспонировать матрицу, то ранг матрицы не изменяется;
- если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
- при удалении нулевого столбца или строки ранг матрицы не изменяется;
- ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
- при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
- ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
- когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .
Пример 2
А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0
r ( A 1 ) = 1 , r ( B 1 ) = 1
А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6
http://lfirmal.com/issledovanie-uravnenij/
http://zaochnik.com/spravochnik/matematika/issledovanie-slau/slau/
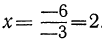
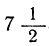
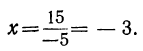
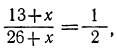
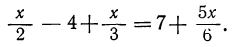
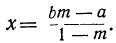
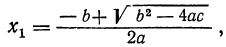
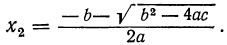
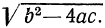
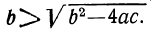
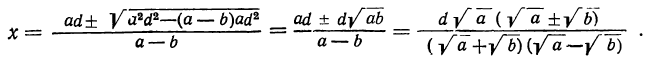
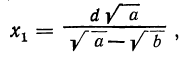
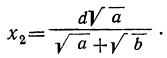
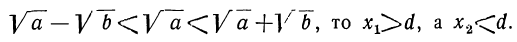
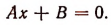

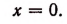
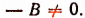
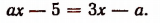
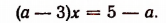
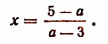
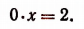
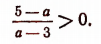

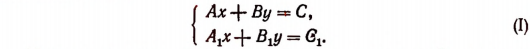
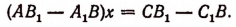
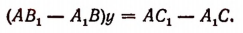
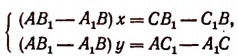
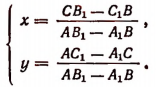
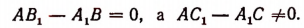
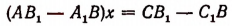
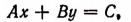
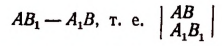
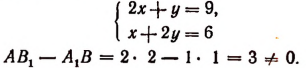
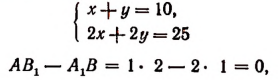
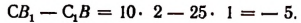
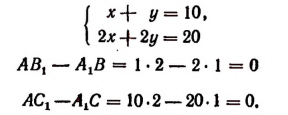
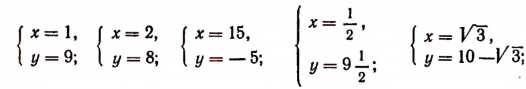
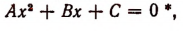
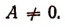
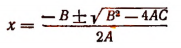
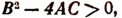 то уравнение имеет два действительных различных корня.
то уравнение имеет два действительных различных корня.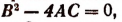 то уравнение имеет два действительных одинаковых корня.
то уравнение имеет два действительных одинаковых корня.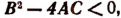 то уравнение имеет два мнимых сопряженных корня.
то уравнение имеет два мнимых сопряженных корня.