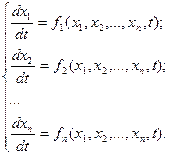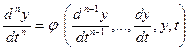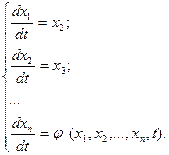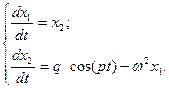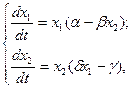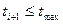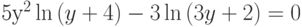Что значит решить уравнение аналитически и численно

Аналитические и численные решения в машинном обучении

Дата публикации 2018-04-13

У вас есть вопросы, такие как:

• Какие данные лучше всего подходят для моей проблемы?
• Какой алгоритм лучше всего подходит для моих данных?
• Как мне лучше настроить мой алгоритм?

Почему эксперт по машинному обучению не может дать вам прямой ответ на ваш вопрос?

В этом посте я хочу помочь вам понять, почему никто не может сказать вам, какой алгоритм использовать или как настроить его для вашего конкретного набора данных.

Я хочу помочь вам увидеть, что нахождение хороших данных / алгоритма / конфигурации на самом делесложная частьприкладного машинного обучения и единственная часть, которую вам нужно сосредоточиться на решении.

Аналитические и численные решения

В математике некоторые проблемы могут быть решены аналитически и численно.

• Аналитическое решение включает в себя постановку задачи в понятной форме и вычисление точного решения.
• Численное решение означает, что нужно угадать решение и проверить, достаточно ли хорошо решена проблема, чтобы остановиться.

Примером является квадратный корень, который может быть решен в обоих направлениях.

Мы предпочитаем аналитический метод в целом, потому что он быстрее и потому что решение является точным. Тем не менее иногда приходится прибегать к численному методу из-за ограничений по времени или аппаратным возможностям.

Хорошим примером является нахождение коэффициентов в уравнении линейной регрессии, которые могут быть рассчитаны аналитически (например, с использованием линейной алгебры), но могут быть решены численно, когда мы не можем вписать все данные в память одного компьютера для выполнения аналитического расчет (например, с помощью градиентного спуска).

Иногда аналитическое решение неизвестно, и все, с чем мы должны работать, это численный подход.

Аналитические решения

Многие проблемы имеют четко определенные решения, которые становятся очевидными после определения проблемы.

Набор логических шагов, которые мы можем выполнить, чтобы рассчитать точный результат.

Например, вы знаете, какую операцию использовать с учетом конкретной арифметической задачи, такой как сложение или вычитание.

В линейной алгебре есть набор методов, которые вы можете использовать дляразложить матрицув зависимости от того, являются ли свойства вашей матрицы квадратными, прямоугольными, содержат действительные или мнимые значения и т. д.

Мы можем распространить это более широко на разработку программного обеспечения, где есть проблемы, которые возникают снова и снова, которые могут быть решены с помощью шаблона проектирования, который, как известно, работает хорошо, независимо от специфики вашего приложения. Такой какшаблон посетителядля выполнения операции над каждым элементом в списке.

Некоторые проблемы в прикладном машинном обучении хорошо определены и имеют аналитическое решение.

Например, метод для преобразования категориальной переменной водна горячая кодировкапростая, повторяемая и (практически) всегда одна и та же методология независимо от количества целочисленных значений в наборе.

К сожалению, большинство проблем, которые мы решаем в машинном обучении, не имеют аналитических решений.

Численные решения

Есть много проблем, которые нас интересуют, которые не имеют точных решений.

Или, по крайней мере, аналитические решения, которые мы уже нашли.

Мы должны угадывать решения и тестировать их, чтобы увидеть, насколько удачное решение. Это включает в себя постановку проблемы и использование проб и ошибок в наборе возможных решений.

По сути, процесс поиска численного решения может бытьописывается как поиск,

Эти типы решений имеют некоторые интересные свойства:

• Мы часто легко можем отличить хорошее решение от плохого.
• Мы часто объективно не знаем, что такое «хорошо«Решение выглядит так; мы можем только сравнить доброту между подходящими решениями, которые мы протестировали.
• Мы часто довольны приблизительным или «достаточно хорошоРешение, а не единственное лучшее решение.

Этот последний пункт является ключевым, потому что часто проблемы, которые мы пытаемся решить с помощью численных решений, являются сложными (поскольку у нас нет простого способа их решения), где любой «достаточно хорошоРешение будет полезным. Это также подчеркивает, что есть много решений для данной проблемы, и даже то, что многие из них могут быть достаточно хорошими, чтобы их можно было использовать.

Большинство проблем, которые нас интересуют в области прикладного машинного обучения, требуют численного решения.

Это хуже чем это.

Численные решения каждой подзадачи на этом пути влияют на пространство возможных решений для последующих подзадач.

Численные решения в машинном обучении

Прикладное машинное обучение представляет собой числовую дисциплину.

Ядром данной модели машинного обучения является проблема оптимизации, которая в действительности представляет собой поиск набора терминов с неизвестными значениями, необходимых для заполнения уравнения. Каждый алгоритм имеет разныеуравнение» а также «термины«Используя эту терминологию свободно

Уравнение легко вычислить, чтобы сделать прогноз для данного набора терминов, но мы не знаем терминов, которые можно использовать, чтобы получить «хорошо» или даже «Лучший«Набор прогнозов для данного набора данных.

Это проблема численной оптимизации, которую мы всегда стремимся решить.

Он численный, потому что мы пытаемся решить проблему оптимизации с помощью шумных, неполных и подверженных ошибкам ограниченных выборок наблюдений из нашей области. Модель изо всех сил пытается интерпретировать данные и создать карту между входами и выходами этих наблюдений.

Более широкое эмпирическое решение в машинном обучении

Задача численной оптимизации, лежащая в основе выбранного алгоритма машинного обучения, вложена в более широкую задачу.

На конкретную проблему оптимизации влияют многие факторы, которые в значительной степени способствуютдобротаКонечного решения, и все они не имеют аналитических решений.

• Какие данные использовать.
• Сколько данных использовать.
• Как обрабатывать данные до моделирования.
• Какой алгоритм моделирования или алгоритмы использовать.
• Как настроить алгоритмы
• Как оценить алгоритмы машинного обучения.

Объективно, все это является частью открытой проблемы, которую представляет ваша конкретная проблема машинного обучения для прогнозирующего моделирования.

Аналитического решения не существует; Вы должны выяснить, какая комбинация этих элементов лучше всего подходит для вашей конкретной проблемы.

Это одна большая проблема поиска, когда комбинации элементов испытываются и оцениваются.

Где вы действительно знаете, каков хороший результат по сравнению с оценками других вариантов решения, которые вы пробовали.

Где нет никакого объективного пути через этот лабиринт, кроме проб и ошибок и, возможно, заимствования идей из других связанных проблем, которые уже знали:достаточно хорошоРешения.

Этот великий эмпирический подход к прикладному машинному обучению часто называют «машинное обучение как поискИ описывается далее в посте:

Это также освещено в посте:

Отвечая на ваш вопрос

Мы возвращаемся к конкретному вопросу, который у вас есть.

Вопрос о том, какие данные, алгоритм или конфигурация будут работать лучше всего для вашей конкретной задачи прогнозного моделирования.

Никто не может взглянуть на ваши данные или описание вашей проблемы и сказать вам, как решить ее лучше или даже лучше.

Опыт может информировать эксперта о тех областях, с которых следует начать поиск, и некоторые из этих ранних догадок могут окупиться, но чаще всего ранние догадки слишком сложны или просто ошибочны.

Проблема прогнозирующего моделирования должна бытьработалдля того, чтобы найти достаточно хорошее решение, и это ваша работа как специалиста по машинному обучению.

Это тяжелая работа прикладного машинного обучения, и это область, в которой нужно практиковаться и получать знания, чтобы считаться компетентными в этой области.

Дальнейшее чтение

Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться.

Резюме

В этом посте вы обнаружили разницу между аналитическими и числовыми решениями и эмпирической природой прикладного машинного обучения.

В частности, вы узнали:

• Аналитические решения — это логические процедуры, которые дают точное решение.
• Численные решения — это процедуры проб и ошибок, которые медленнее и приводят к приближенным решениям.
• В основе прикладного машинного обучения лежит численное решение с откорректированным мышлением, позволяющее выбирать данные, алгоритмы и конфигурации для конкретной задачи прогнозного моделирования.

У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.

Аналитическое и численное решения дифференциальных уравнений

Дата добавления: 2013-12-23 ; просмотров: 4404 ; Нарушение авторских прав

Модель колебаний сердечной мышцы.

К системе дифференциальных уравнений первой степени.

Переход от дифференциального уравнения высокой степени

В случаях, когда модель изучаемого процесса описывается ДУ степенью большей 1, удобно трансформировать его в систему ДУ первой степени. Именно такой стандартизованной формы требуют, например, многие математические пакеты для проведения операции численного решения ДУ (см. далее).

Напомним, что системой ДУ первой степени называется система вида:

К ней легко приводится ДУ степени n:

Приведение осуществляется путем замены переменных:

,

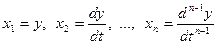
которая дает каноническую систему ДУ первой степени:

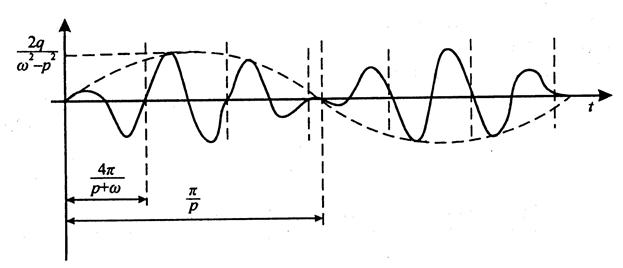
Рассмотрим пример. Модель колебаний сердечной мышцы (изменение ее длины y в продольном направлении) можно упрощенно описать ДУ следующего вида:

,

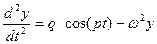
где p, q – постоянные коэффициенты, определяющие параметры периодического изменения возмущающего воздействия (мышечного напряжения), 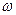— угловая собственная (резонансная) частота колебаний сердечной мышцы.

Произведем замену переменных: 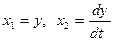. Получим:

Общее аналитическое решение данной системы в графическом виде будет иметь вид (подробно ход получения решения не приводится):

,

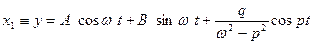
где A и B – постоянные коэффициенты.

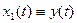
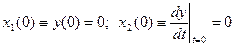
График решения системы при начальных условиях имеет вид:

Аналитическим решением ДУ называется нахождение зависимостей его переменных от времени в виде явно заданной математической формулы.

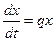
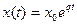
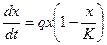
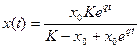
Например, для модели Мальтуса таким аналитическим решением является формула , для модели Ферхюльста аналитическим решением является формула , а вот ДУ модели Вольтера-Лотка:

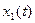
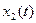
не имеют общего аналитического решения. То есть, иными словами, интегралы, возникающие в правой части выражений для и невозможно «взять», используя стандартные приемы аналитического интегрирования (см. курс высшей математики). Откуда же взялись приведенные в описании этой модели графики зависимостей переменных от времени и фазовые траектории? Они были получены путем численного решения приведенной системы ДУ.

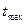
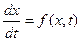
В общем случае численное решение ДУ сводится к замене дифференциалов, входящих в его состав, малыми приращениями соответствующих переменных и нахождение решений получившегося алгебраического уравнения на интервале времени от 0 до любого заранее заданного . Рассмотрим применение простейшего метода численного решения – метода Эйлера для решения ДУ первого порядка .

Представим исходное ДУ в виде:

,

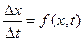
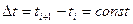
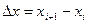
где — дискретность по времени, произвольно выбранная малая величина; ; i – шаг алгоритма.

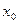
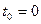
Шаг 0. Задаем начальное условие и определяем .

Шаг 1. Вычисляем первые значения x и t по формулам:

;

.

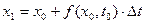
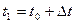
Шаги 2 — n. Продолжаем вычисление x и t по формулам:

;

.

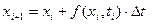
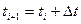
до тех пор пока

Аналогичным образом можно решать и системы ДУ первого порядка, к которым, как мы теперь знаем, можно свести ДУ любого порядка.

Точность численного решения при прочих равных условиях определяется выбранной величиной дискретности по времени 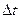. Чем меньше дискретность, тем точнее решение, но и тем больше шагов должен включать алгоритм. Именно по причине того, что алгоритмы численного решения ДУ требуют огромного количества элементарных вычислений (число шагов может составлять сотни и тысячи), для их практической реализации используют компьютеры. Широко используемые программы математического моделирования, как правило, имеют в своем составе стандартные функции численного решения ДУ, поэтому их пользователю нет нужды детально разбираться в тонкостях используемых алгоритмов – достаточно задать свои ДУ, начальные условия и интервал времени, на котором ищется решения. Все остальное программа сделает самостоятельно.

Простота использования описанных выше функций привела к тому, что создатели математических моделей в настоящее время обычно даже и не пытаются найти аналитическое решение разработанных ими ДУ, предпочитая во всех случаях решать их численно. Справедливости ради следует отметить, что абсолютное большинство ДУ, используемых в современном моделировании, не имеет аналитического решения в принципе.

Сказанное выше не отменяет необходимости при моделировании выполнять качественный анализ ДУ, в первую очередь путем исследования устойчивости стационарных состояний и типов поведения системы вблизи этих состояний.

Решение уравнений

Цель лекции. Показать технику численного решения нелинейных уравнений с использованием сервисов MathCAD. Показать различные методы аналитического решения систем линейных уравнений.

4.1. Численное решение нелинейных уравнений

Относительно небольшое количество задач решения уравнений можно решить аналитически. Аналитическое решение предполагает точное определение корней либо нахождение алгоритма, по которому корни всегда могут быть найдены. На практике часто приходится искать решение при помощи численных методов [1, 11]. Уравнения решаются численными методами с заданной погрешностью. В MathCAD погрешность задается системной константой TOL . Как правило, отыскание корней алгебраического уравнения (или системы уравнений) численными методами связано с двумя задачами:

• локализация корней, т. е. определение их существования в принципе, а также исследование их количества и примерного расположения;
• собственно отыскание корней с заданной погрешностью

Для численного решения уравнений в MathCAD существуют встроенные функции[1, 10], в которых реализованы алгоритмы известных численных методов: итерационный метод секущих ; различные градиентные методы и другие. Почти все встроенные функции предполагают, что корни уже приблизительно локализованы.

Использование функции root()

Рассмотрим решение простейших уравнений вида F(x)=0 . Решить уравнение – значит найти все его корни, т.е. такие числа, при подстановке которых в исходное уравнение получим верное равенство. Если функция нескольких аргументов F(x, у, ..)=0. , все остальные значения должны быть заданы для искомого x . Для локализации корней (исследования их количества и примерного расположения) полезно построить график функции и определить все точки пересечения графика функции с осью OX.

Функция root () вычисляет значение переменной, при котором F(x, у, ..)=0 . Если уравнение имеет несколько корней, функцию надо вызывать соответствующее число раз. Вычисления реализуются итерационным методом. Данный метод заключается в постепенном приближении к искомому корню с некоторой точностью от начального значения переменной. Точность вычислений задаётся системной переменной TOL , определённой в меню Tools/ Worksheet Options .. По умолчанию равной 0.001.

root(F(x, у, . ), x, [a, b]) возвращает с заданной точностью значение переменной, x , лежащей между a и b при котором функция равна нулю. Значения F() для a и b должны быть разных знаков. Третий аргумент не обязателен. Выбор решения определяется выбором начального значения переменной

Пример 4.1

Решить уравнение