Понимание эквивалентных уравнений в алгебре
Понимание эквивалентных уравнений в алгебре — Науки
Содержание:
Эквивалентные уравнения — это системы уравнений, которые имеют одинаковые решения. Выявление и решение эквивалентных уравнений — ценный навык не только на уроках алгебры, но и в повседневной жизни. Взгляните на примеры эквивалентных уравнений, как решить их для одной или нескольких переменных и как вы можете использовать этот навык за пределами классной комнаты.
Ключевые выводы
- Эквивалентные уравнения — это алгебраические уравнения, которые имеют одинаковые решения или корни.
- Добавление или вычитание одного и того же числа или выражения к обеим сторонам уравнения дает эквивалентное уравнение.
- Умножение или деление обеих частей уравнения на одно и то же ненулевое число дает эквивалентное уравнение.
Линейные уравнения с одной переменной
В простейших примерах эквивалентных уравнений нет переменных. Например, эти три уравнения эквивалентны друг другу:
- 3 + 2 = 5
- 4 + 1 = 5
- 5 + 0 = 5
Признать, что эти уравнения эквивалентны, — это здорово, но не особенно полезно. Обычно задача эквивалентного уравнения просит вас решить для переменной, чтобы убедиться, что она такая же (та же корень) как одно в другом уравнении.
Например, следующие уравнения эквивалентны:
В обоих случаях x = 5.Откуда нам это знать? Как вы решите это для уравнения «-2x = -10»? Первый шаг — узнать правила эквивалентных уравнений:
- Добавление или вычитание одного и того же числа или выражения к обеим сторонам уравнения дает эквивалентное уравнение.
- Умножение или деление обеих частей уравнения на одно и то же ненулевое число дает эквивалентное уравнение.
- Возведение обеих частей уравнения в одну и ту же нечетную степень или получение одного и того же нечетного корня приведет к эквивалентному уравнению.
- Если обе части уравнения неотрицательны, возведение обеих сторон уравнения в одну четную степень или получение одного и того же четного корня даст эквивалентное уравнение.
пример
Применяя эти правила на практике, определите, эквивалентны ли эти два уравнения:
- х + 2 = 7
- 2x + 1 = 11
Чтобы решить эту проблему, вам нужно найти «x» для каждого уравнения. Если «x» одинаково для обоих уравнений, то они эквивалентны. Если «x» отличается (т.е. уравнения имеют разные корни), то уравнения не эквивалентны. Для первого уравнения:
- х + 2 = 7
- x + 2-2 = 7-2 (вычитая обе части на одно и то же число)
- х = 5
Для второго уравнения:
- 2x + 1 = 11
- 2x + 1-1 = 11-1 (вычитая обе части на одно и то же число)
- 2x = 10
- 2x / 2 = 10/2 (разделив обе части уравнения на одно и то же число)
- х = 5
Итак, да, два уравнения эквивалентны, потому что x = 5 в каждом случае.
Практические эквивалентные уравнения
Вы можете использовать эквивалентные уравнения в повседневной жизни. Это особенно полезно при покупках. Например, вам нравится определенная рубашка. Одна компания предлагает рубашку за 6 долларов с доставкой за 12 долларов, в то время как другая компания предлагает рубашку за 7,50 долларов с доставкой за 9 долларов. Какая рубашка имеет лучшую цену? Сколько рубашек (может быть, вы хотите подарить друзьям) вам придется купить, чтобы цена была одинаковой для обеих компаний?
Чтобы решить эту проблему, пусть x будет числом рубашек. Для начала установите x = 1 для покупки одной рубашки. Для компании №1:
- Цена = 6x + 12 = (6) (1) + 12 = 6 + 12 = 18 $
- Цена = 7,5x + 9 = (1) (7,5) + 9 = 7,5 + 9 = 16,50 $
Итак, если вы покупаете одну рубашку, вторая компания предлагает более выгодную сделку.
Чтобы найти точку, в которой цены равны, оставьте «x» числом рубашек, но приравняйте два уравнения друг к другу. Чтобы узнать, сколько рубашек вам нужно купить, решите для «x»:
- 6х + 12 = 7,5х + 9
- 6x — 7,5x = 9-12 (вычитая одинаковые числа или выражения с каждой стороны)
- -1,5х = -3
- 1,5x = 3 (деление обеих сторон на одно и то же число, -1)
- x = 3 / 1,5 (деление обеих сторон на 1,5)
- х = 2
Если вы покупаете две рубашки, цена будет одинаковой, независимо от того, где вы ее купите. Вы можете использовать ту же математику, чтобы определить, какая компания предлагает вам более выгодную сделку с крупными заказами, а также рассчитать, сколько вы сэкономите, используя одну компанию по сравнению с другой. Видите ли, алгебра полезна!
Эквивалентные уравнения с двумя переменными
Если у вас есть два уравнения и две неизвестные (x и y), вы можете определить, эквивалентны ли два набора линейных уравнений.
Например, если вам даны уравнения:
Вы можете определить, эквивалентна ли следующая система:
Чтобы решить эту проблему, найдите «x» и «y» для каждой системы уравнений. Если значения совпадают, то системы уравнений эквивалентны.
Начнем с первого подхода. Чтобы решить два уравнения с двумя переменными, выделите одну переменную и подставьте ее решение в другое уравнение. Чтобы изолировать переменную «y»:
- -3x + 12y = 15
- -3x = 15–12 лет
- x = — (15 — 12y) / 3 = -5 + 4y (подставьте «x» во втором уравнении)
- 7x — 10y = -2
- 7 (-5 + 4лет) — 10лет = -2
- -35 + 28–10 лет = -2
- 18лет = 33
- у = 33/18 = 11/6
Теперь вставьте «y» обратно в любое уравнение, чтобы найти «x»:
Проработав это, вы в конечном итоге получите x = 7/3.
Чтобы ответить на вопрос, вы мог примените те же принципы ко второму набору уравнений, чтобы решить для «x» и «y», чтобы обнаружить, что да, они действительно эквивалентны. В алгебре легко увязнуть, поэтому неплохо проверить свою работу с помощью онлайн-программы для решения уравнений.
Однако умный ученик заметит, что две системы уравнений эквивалентны без каких-либо сложных вычислений. Единственная разница между первым уравнением в каждом наборе состоит в том, что первое в три раза больше второго (эквивалентного). Второе уравнение точно такое же.
Системы линейных уравнений
Глава 5. Системы линейных уравнений
Определение. Матрицей называется прямоугольная таблица, составленная из чисел.
Числа, записанные в матрице, называются её элементами. При этом они могут быть как действительными, так и комплексными. Пример:
A =
Наша матрица A состоит из 3 строк и 4 столбцов. Будем записывать это так, что (3, 4) − размер матрицы A (иногда пишут 3×4, но × легко перепутать с x, особливо в рукописном тексте). Вообще, если в матрице s строк и n столбцов, то её размером считается запись (s, n). Матрицу обрамляют круглыми скобками: (). В литературе вы можете встретить другие обозначения: || || или []. Если s = n, то матрица называется квадратною. Матрицу размера (n, n) называют также квадратною матрицею n—го порядка.
Если надобно записать матрицу в общем (буквенном) виде, то пишут так:
A =
Это матрица размера (s, n), каждый её элемент обозначен одной и той же буквою − обыкновенно (хотя и не обязательно) это та же буква, которая обозначает самоё матрицу, но строчная. Эта буква снабжена двойными индексами: a11 − это не ‘a одиннадцать’, а ‘a один-один’. Первый индекс означает номер строки, в которой стоит данный элемент, второй − номер столбца. Разделителей между индексами обыкновенно не пишут, доколе это не может привести к неопределённости; к примеру, запись a211 непонятна: не то это a2,11, не то a21,1. В этом случае разделитель обязателен (здесь это запятая).
Среди всех матриц выделим матрицы, состоящие из одного столбца, т. е. размера (s, 1):

Такую матрицу назовём матрицей—столбцом, или вектор—столбцом. Аналогично матрицу вида
размера (1, n) назовём матрицей—строкой, или вектор—строкой.
5.1.2. Ступенчатая матрица
Определение 1. Строка матрицы называется нулевой строкой, если она состоит из одних нулей.
Определение 2. Главным элементом какой-либо ненулевой строки данной матрицы называется первый ненулевой элемент этой строки, считая слева направо.
Нулевая строка не имеет главного элемента, все остальные строки имеют однозначно определённый главный элемент. В любой матрице число главных элементов равно числу ненулевых строк.
Определение 3. Матрица называется ступенчатой, если для любых двух её последовательных строк выполняется одно из двух условий:
1) вторая строка состоит из одних нулей (нулевая строка);
2) обе строки ненулевые, и при этом главный элемент первой строки расположен строго левее главного элемента второй строки.
Из этого определения легко понять, что нулевые строки концентрируются в конце (внизу) матрицы, составляя нулевой блок (блок нулевых строк). В самом деле, если какая-либо строка нулевая, то в силу первой части определения все последующие строки также нулевые. Впрочем, нулевых строк может и вовсе не быть.
Определение 4. Матрица называется главной ступенчатой, если она является ступенчатой и сверх того
3) все главные элементы равны единице;
4) выше главных единиц (в тех же столбцах) стоят одни нули.
Из определения ясно, что каждый главный столбец главной ступенчатой матрицы устроен так, что в одной позиции стоит 1, а в остальных позициях − нули. (Ниже 1 стоят нули из-за того, что матрица является ступенчатой.) При этом номер позиции (строки), в которой стоит 1, равен номеру этого столбца в череде главных столбцов.
5.1.3. Элементарные преобразования
Определение 1. Элементарным преобразованием первого типа над строками какой-либо матрицы называется перестановка местами двух произвольных строк этой матрицы.
Определение 2. Элементарным преобразованием второго типа называется умножение произвольной строки данной матрицы на какое-либо число, не равное 0.
Определение 3. Элементарным преобразованием третьего типа называется прибавление к какой-либо строке данной матрицы другой строки, умноженной предварительно на любое число[1].
5.1.4. Теорема C. F. Gauss’а[2]
Теорема (C. F. Gauss’а). Любую матрицу с помощью нескольких элементарных преобразований над строками можно привести к главному ступенчатому виду.
Доказательство. Будем рассматривать матрицы размера (s, n). Обозначим через N сумму числа строк и столбцов: N = s + n. Доказательство поведём индукцией по этому параметру N. Наименьшее возможное значение N равно 2 (для матриц размера (1, 1)).
Основание (база) индукции. Пусть наша матрица A имеет размер (1, 1). Тогда A = = (a11). Если a11 = 0, то матрица уже главная ступенчатая. Если же нет, то разделим (единственную) строку матрицы A на a11, получим матрицу (1), которая уже является главной ступенчатой.
Индуктивный переход. Пусть теорема C. F. Gauss’а справедлива для любой матрицы, у которой s + n 1 вычтем из i-й строки матрицы D её первую строку, предварительно умножив её на число di1. После этой серии элементарных преобразований в новой матрице E все элементы первого столбца, кроме первого, станут равными нулю. Обозначим через F матрицу, получающуюся из E вычёркиванием первой строки и первого столбца. Её размеры меньше размеров матрицы A, и поэтому её можно привести к главному ступенчатому виду G с помощью серии элементарных преобразований над её строками, что равносильно совершению таких же элементарных преобразований над матрицей E. Пусть матрица E привелась таким образом к матрице H. Матрица H уже ступенчатая, но не обязательно главная ступенчатая. Возьмём какой-нибудь главный столбец матрицы G. Пусть главная единица нашего столбца стоит в k-й строке и l-м столбце матрицы H.
Вычтем из первой строки матрицы H её k-ю строку, умноженную предварительно на число h1l, и первый элемент нашего столбца обнулится. Важно, что при этом никак не затрагивается первый столбец, − он остаётся неизменным. Произведём указанную операцию с каждым главным столбцом матрицы G. Ясно, что новая матрица уже будет главной ступенчатой. Теорема доказана.
5.1.5. Обратимость элементарных преобразований
Предложение. Если над матрицей A совершено элементарное преобразование какого-либо типа, приводящее её к матрице B, то существует элементарное преобразование того же типа, приводящее матрицу B снова к матрице A.
Доказательство. Это очевидно для преобразований первого и второго типов. В самом деле, если мы совершили перестановку строк, то вторичная перестановка тех же строк вернёт нас к исходной матрице. Если мы умножили некоторую строку на ненулевое число, то умножение той же строки на обратное число вернёт нас к исходной матрице. Допустим теперь, что в данной матрице A мы прибавили к i-й строке j-ю строку (i ≠ j), предварительно умноженную на число α, и таким образом пришли к матрице B. Утверждаю, что можно вернуться к матрице A, если прибавить к i-й строке матрицы B её j-ю строку, предварительно умноженную на число −α. Так как при обоих преобразованиях все строки, кроме i-й, вообще не менялись, то достаточно посмотреть, что произойдёт с каким-нибудь элементом bik матрицы B. Вычисляем:
т. е. мы вернулись к матрице A, QED.
§ 5.2. Системы линейных уравнений
5.2.1. Основные определения
Определение 1. Система уравнений вида
называется системой линейных алгебраических уравнений с неизвестными x1, x2, …, xn.
Числа aij называются коэффициентами системы, bi − её свободными членами.
Определение 2. Решением системы (1) называется такой набор чисел 
Определение 3. Решить систему (1) − значит найти все её решения (множество всех решений).
Определение 4. Система (1) называется совместною, если она имеет хотя бы одно решение (множество всех решений непусто), и несовместною в противном случае, т. е. если она не имеет решений (множество всех решений пусто).
Определение 5. Система (1) называется определённою, если она имеет ровно одно решение, и неопределённою, если имеет более одного решения.
Мы очень скоро увидим, что неопределённая система имеет бесконечно много решений.
5.2.2. Элементарные преобразования над системами уравнений
Определение 1. Элементарным преобразованием первого типа над системой уравнений называется перестановка местами двух произвольных уравнений системы.
Определение 2. Элементарным преобразованием второго типа называется умножение любого уравнения системы на какое-либо число, не равное 0.
Определение 3. Элементарным преобразованием третьего типа называется прибавление к какому-либо уравнению другого уравнения, умноженного предварительно на любое число[3].
Каждой системе уравнений вида (1) можно поставить в соответствие две матрицы: матрицу системы и расширенную матрицу системы.
Определение 4. Матрицей системы уравнений (1) называется матрица, составленная из коэффициентов системы:

Определение 5. Расширенной матрицей системы уравнений (1) называется матрица, составленная из коэффициентов системы и свободных членов:

Иногда в расширенной матрице отделяют столбец свободных членов вертикальной чертой (сплошной или прерывистой), но это не обязательно. Ясно, что матрица системы не даёт полной информации о системе в отличие от расширенной матрицы, по которой можно однозначно восстановить систему уравнений, если только мы знаем список неизвестных (буквы, которыми были обозначены неизвестные). Впрочем, последнее не так существенно, потому что ведь мы в первую очередь интересуемся решениями, а каждое решение представляет собою просто набор чисел без обозначений неизвестных.
Определение 6. Пусть даны две системы уравнений относительно одного и того же набора неизвестных x1, x2, …, xn. Говорят, что система (2) является следствием системы (1), если каждое решение системы (1) является решением системы (2).
Другими словами, множество всех решений системы (1) есть подмножество (часть) множества всех решений системы (2).
Определение 7. Две системы уравнений относительно одного и того же набора неизвестных x1, x2, …, xn называются эквивалентными, или равносильными, если множества их решений совпадают, или, что то же, каждая из них является следствием другой.
Иными словами, две системы эквивалентны тогда и только тогда, когда каждое решение первой системы является решением второй и, наоборот, каждое решение второй системы является решением первой.
Предложение. При совершении одного элементарного преобразования система уравнений переходит в эквивалентную систему.
Доказательство. Достаточно доказать, что вторая система является следствием первой. Действительно, предположив, что это уже доказано, совершим обратное элементарное преобразование, которое вернёт нас к исходной системе (см. п. 5.1.5). По доказанному первая система тогда будет следствием второй, и всё доказано.
Докажем, что вторая система является следствием первой. Для преобразований первых двух типов это совершенно очевидно. Совершим преобразование третьего типа, прибавив к i-й строке j-ю строку, умноженную предварительно на число α. При этом изменится только i-е уравнение, поэтому я здесь выпишу только его:
Пусть 
Если подставить наше решение в новую систему, то все равенства, кроме i-го, будут выглядеть точно так же и поэтому выполняются. i-е же равенство будет выглядеть так:
Чтобы убедиться, что оно тоже выполняется, достаточно взять i-е равенство системы (1*) верных числовых равенств и прибавить к нему j-е равенство той же системы, предварительно умножив его на α. Предложение доказано.
5.2.3. Теорема C. F. Gauss’а (о системах линейных уравнений)
Лемма. Если в системе линейных уравнений совершить одно элементарное преобразование, то расширенная матрица новой системы может быть получена из расширенной матрицы старой системы с помощью совершения аналогичного (точно такого же, я буду говорить одноимённого) преобразования.
Доказательство: это очевидно.
Следствие. Если в расширенной матрице A системы линейных уравнений (1) совершить одно элементарное преобразование над её строками и таким образом прийти к новой матрице B, а затем одноимённое преобразование совершить над системой уравнений (1), то расширенная матрица новой системы (2) совпадёт с матрицей B.
Доказательство. В силу леммы расширенная матрица системы (2) может быть получена из матрицы A, т. е. расширенной матрицы системы (1), с помощью совершения преобразования, одноимённого тому, которое было совершено нами над системой уравнений (1). С другой стороны, это последнее преобразование было одноимённо тому, которое мы совершили над матрицей A. Таким образом, расширенная матрица системы (2) может быть получена из A с помощью того же самого преобразования, которое мы в самом начале совершили над матрицей A. Значит, эта новая расширенная матрица совпадает с B, QED.
Теорема (C. F. Gauss’а, о системах линейных уравнений). Всякая система линейных уравнений с помощью конечного числа элементарных преобразований может быть приведена к такой системе уравнений, расширенная матрица которой является главной ступенчатой.
Доказательство. Приведём расширенную матрицу данной системы уравнений с помощью серии элементарных преобразований над её строками к главному ступенчатому виду. Теперь будем совершать над самой данной системой одноимённые преобразования. По следствию из леммы на каждом этапе очередная матрица будет расширенной матрицей соответствующей системы уравнений. Значит, и последняя, главная ступенчатая, матрица будет служить расширенной матрицей последней системы, QED.
Важно, что на каждом этапе в силу предложения из предыдущего пункта система уравнений переходит в эквивалентную. На этом основан метод C. F. Gauss’а решения систем, при котором система приводится с помощью серии элементарных преобразований к главному ступенчатому виду. Множество всех решений системы при этом не меняется, так что достаточно решить последнюю систему. А системы, имеющие главный ступенчатый вид, решаются очень легко, как будет видно из следующего пункта.
5.2.4. Решение ступенчатых систем уравнений
Рассмотрим систему линейных уравнений, расширенная матрица которой является главной ступенчатой. Допуская известную вольность речи, будем такие системы называть ступенчатыми.
Определение. В ступенчатой системе уравнений неизвестные, соответствующие главным столбцам, называются главными неизвестными, все остальные − свободными неизвестными.
Здесь надлежит различать три случая.
1°. Столбец свободных членов является главным. В этом случае система несовместна.
В самом деле, пусть главный элемент последнего столбца расширенной матрицы (т. е. столбца свободных членов) находится в i-й строке. Тогда i-е уравнение имеет следующий вид:
(Напомню, что все главные элементы главной ступенчатой матрицы равны 1, а левее любого главного элемента всегда стоят одни нули.) Ясно, что такое уравнение не имеет решений, тем более не может иметь решений вся наша система.
2°. Все столбцы, кроме последнего, главные. (Другими словами: нет свободных неизвестных, а столбец свободных членов не является главным, т. е. не содержит главных элементов.) В этом случае в i-м столбце на i-м месте стоит 1 (i ≤ n), на остальных местах − нули. После отбрасывания нулевых уравнений придём к эквивалентной системе, которая в нашем случае приобретает следующий вид:
Ясно, что такая система имеет решение, и притом единственное, а именно, 
3°. Есть свободные неизвестные, но столбец свободных членов не является главным. Покажем, что в этом случае система имеет бесконечно много решений (и, следовательно, является неопределённой). Отбросим в расширенной матрице нулевые строки (они сосредоточены внизу матрицы), что приведёт к эквивалентной системе. Можно считать, что исходная расширенная матрица не была нулевой (для нулевой матрицы доказываемое утверждение очевидно), так что хотя бы одна строка останется. Теперь число строк в матрице равно числу главных неизвестных. Для удобства переобозначим неизвестные: пусть y1, y2, …, yr − главные неизвестные, а z1, z2, …, zn−r − свободные. Разнесём теперь неизвестные в разные части: главные неизвестные оставим в левых частях уравнений, а свободные перенесём в правые части, естественно, с противоположным знаком (свободные члены также остаются в правых частях). Получится система, эквивалентная исходной, следующего вида:
Мы видим, что здесь все главные неизвестные явно выражены через свободные, причём эти выражения (правые части) представляют собою линейные функции, т. е. линейные комбинации свободных неизвестных плюс свободный член. Как же решить получившуюся систему? Придадим свободным неизвестным произвольные значения и вычислим по написанным формулам соответствующие значения главных неизвестных. Очевидно, что в совокупности мы получим решение нашей системы. Более того, каждое решение можно получить таким способом при подходящем выборе свободных неизвестных, так как все неизвестные всегда будут связаны соотношениями (3). В этом смысле формулы (3) описывают множество всех решений нашей системы, т. е задают, как говорят, её общее решение. И ясно, что решений будет бесконечно много, потому что хотя бы одно свободное неизвестное у нас есть, значит, придать определённые значения свободным неизвестным мы можем бесконечным числом различных способов, и получающиеся решения будут различны.
Попутно мы фактически доказали следующие два утверждения.
Теорема 1 (критерий совместности ступенчатой системы). Система уравнений, расширенная матрица которой имеет главный ступенчатый вид, совместна тогда и только тогда, когда столбец свободных членов не является главным.
Теорема 2. Если система линейных уравнений имеет более одного решения, то она имеет бесконечно много решений.
Таким образом, линейная система не может иметь, например, ровно семь решений.
5.2.5. Однородные системы уравнений
Так называются системы линейных уравнений, в которых все свободные члены равны нулю:
Такая система всегда совместна, т. к. она всегда имеет решение 
Теорема. Если в однородной системе линейных уравнений (4) число уравнений s строго меньше числа неизвестных n, то такая система имеет хотя бы одно нетривиальное решение.
Доказательство. Приведём нашу систему к главному ступенчатому виду. На всех этапах однородность, очевидно, сохраняется. После отбрасывания нулевых уравнений мы получим однородную систему уравнений, эквивалентную исходной. Число её уравнений строго меньше числа неизвестных, так как число неизвестных не изменилось, а число уравнений даже могло уменьшиться. Но число строк теперь равно числу главных элементов, а значит, числу главных столбцов и числу главных неизвестных. Таким образом, число главных неизвестных строго меньше общего числа неизвестных. Значит, есть свободные неизвестные, а тогда система неопределённая (нулевой столбец свободных членов не может быть главным) и имеет бесконечно много решений. Значит, есть и ненулевые решения, QED.
[1] При этом результат ставится в первую из этих двух строк, а вторая из них, равно как и все остальные строки матрицы, не меняется.
[2] ́дрих Га́усс (нем. Johann Carl Friedrich Gauß; 30 апреля 1777, Брауншвейг − 23 февраля 1855, Гёттинген) − великий немецкий математик, астроном и физик, считается одним из величайших математиков всех времён.
[3] При этом результат ставится на место первого из этих двух уравнений, а второе из них, равно как и все остальные, не меняется.
Эквивалентные системы линейных уравнений
Две системы линейных уравнений от одного набора x1. xn неизвестных и соответственно из m и p уравнений
называются эквивалентными, если их множества решений 


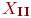





Элементарные преобразования систем линейных уравнений (строк матриц)
Определение 3.4.1 (элементарное преобразование 1-го типа). При 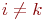

т. е. в новом i -м уравнении aij’=aij+cakj, bi’=bi+cbk.
Определение 3.4.2 (элементарное преобразование 2-го типа). При 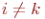
| 53. Метод Гаусса решения систем линейных уравнений | |||||||||||||
Формулы Крамера и матричный метод решения систем линейных уравнений не имеют серьезного практического применения, так как связаны с громоздкими выкладками. Практически для решения систем линейных уравнений чаще всего применяется метод Гаусса, состоящий в последовательном исключении неизвестных по следующей схеме. Для того чтобы решить систему уравнений выписывают расширенную матрицу этой системы 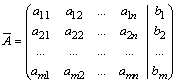 и над строками этой матрицы производят элементарные преобразования, приводя ее к виду, когда ниже главной диагонали, содержащей элементы и над строками этой матрицы производят элементарные преобразования, приводя ее к виду, когда ниже главной диагонали, содержащей элементы  будут располагаться нули. Разрешается: 1) изменять порядок строк матрицы, что соответствует изменению порядка уравнений; 2) умножать строки на любые отличные от нуля числа, что соответствует умножению соответствующих уравнений на эти числа; 3) прибавлять к любой строке матрицы другую, умноженную на отличное от нуля число, что соответствует прибавлению к одному уравнению системы другого, умноженного на число. С помощью этих преобразований каждый раз получается расширенная матрица новой системы, равносильной исходной, т. е. такой системы, решение которой совпадает с решением исходной системы. Рассмотрим метод Гаусса на примерах. Пример 14. Установить совместность и решить систему будут располагаться нули. Разрешается: 1) изменять порядок строк матрицы, что соответствует изменению порядка уравнений; 2) умножать строки на любые отличные от нуля числа, что соответствует умножению соответствующих уравнений на эти числа; 3) прибавлять к любой строке матрицы другую, умноженную на отличное от нуля число, что соответствует прибавлению к одному уравнению системы другого, умноженного на число. С помощью этих преобразований каждый раз получается расширенная матрица новой системы, равносильной исходной, т. е. такой системы, решение которой совпадает с решением исходной системы. Рассмотрим метод Гаусса на примерах. Пример 14. Установить совместность и решить систему 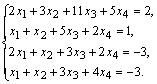 Решение. Выпишем расширенную матрицу системы и поменяем местами первую и вторую строки для того, чтобы элемент Решение. Выпишем расширенную матрицу системы и поменяем местами первую и вторую строки для того, чтобы элемент 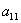 равнялся единице (так удобнее производить преобразования матрицы). равнялся единице (так удобнее производить преобразования матрицы). 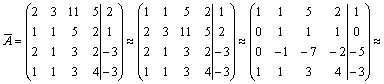  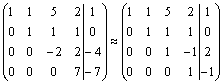 . Имеем . Имеем  Ранги матрицы системы и ее расширенной матрицы совпали с числом неизвестных. Согласно теореме Кронекера-Капелли система уравнений совместна и решение ее единственно. Выпишем систему уравнений, расширенную матрицу которой мы получили в результате преобразований: Ранги матрицы системы и ее расширенной матрицы совпали с числом неизвестных. Согласно теореме Кронекера-Капелли система уравнений совместна и решение ее единственно. Выпишем систему уравнений, расширенную матрицу которой мы получили в результате преобразований:  Итак, имеем Итак, имеем  Далее, подставляя Далее, подставляя  в третье уравнение, найдем в третье уравнение, найдем  Подставляя Подставляя  и и 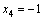 во второе уравнение, получим во второе уравнение, получим  и, наконец, подставляя в первое уравнение найденные и, наконец, подставляя в первое уравнение найденные  получим получим  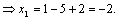 Таким образом, имеем решение системы Таким образом, имеем решение системы  54. Однородные системы линейных уравнений Однородной системой m линейных уравнений с n неизвестными называется система вида 54. Однородные системы линейных уравнений Однородной системой m линейных уравнений с n неизвестными называется система вида
Эта система может быть записана в виде матричного уравнения и операторного уравнения
Система (1) всегда совместна, так как: имеет очевидное решение x10 = x20 = … = xn0 = 0 , которое называется нулевым, или тривиальным; добавление нулевого столбца не меняет ранга матрицы, следовательно, выполняется достаточное условие теоремы Кронекера–Капелли; θ О Img ^A , так как Img ^A — линейное пространство. Естественно, нас интересуют нетривиальные решения однородной системы. Условие нетривиальной совместности: Для того, чтобы однородная система имела нетривиальное решение, необходимо и достаточно, чтобы ранг ее основной матрицы был меньше числа неизвестных. Доказательство см. в книге О.В. Зиминой «Линейная алгебра и аналитическая геометрия», стр. 77. Следствие. Для того, чтобы однородная система n линейных уравнений с n неизвестными (матрица системы A — квадратная) имела нетривиальное решение, необходимо и достаточно, чтобы определитель матрицы этой системы был равен нулю ( det A = 0 ). Общим решением системы линейных уравнений называется формула, которая определяет любое ее решение. Так как система (1) эквивалентна операторному уравнению (2), то множество всех ее решений есть ядро оператора ^A . Пусть Ker ^A ≠ θ , Rg ^A = r и x1, x2, … , xn − r — базис в ядре оператора. Фундаментальной системой решений однородной системы (1) называется базис ядра оператора ^A (точнее, координатные столбцы базисных векторов в Ker ^A ). Это определение можно сформулировать несколько иначе: Фундаментальной системой решений однородной системы (1) называется n − r линейно независимых решений этой системы. Будем обозначать координатные столбцы базисных векторов в Ker ^A X1, X2, … , Xn − r . Теорема о структуре общего решения однородной системы уравнений: Любое решение однородной системы линейных уравнений определяется формулой
где X1, X2, … , Xn − r — фундаментальная система решений однородной системы линейных уравнений и C1, C2, … , Cn − r — произвольные постоянные. Свойства общего решения однородной системы уравнений: При любых значениях C1, C2, … , Cn − r X , определяемое формулой (3), является решением системы (1). Каково бы ни было решение X0 , существуют числа C10, … , Cn − r0 такие, что
Вывод: Чтобы найти фундаментальную систему и общее решение однородной системы, нужно найти базис ядра соответствующего линейного оператора. источники: http://pandia.ru/text/78/222/99293.php http://lektsii.org/7-2182.html |












