Чувствительность системы линейных уравнений к изменению коэффициентов

Чувствительность системы линейных уравнений к изменению коэффициентов

Системой m линейных уравнений с n неизвестными называется система вида

где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные. В обозначении коэффициентов a_ij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы.

Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих неизвестных x₁,…,x_n.

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

1. Система может иметь единственное решение.
2. Система может иметь бесконечное множество решений. Например, . Решением этой системы является любая пара чисел, отличающихся знаком.
3. И третий случай, когда система вообще не имеет решения. Например, , если бы решение существовало, то x₁ + x₂ равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

Рассмотрим способы нахождения решений системы.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

или короче A∙X=B.

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.

Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A: . Поскольку A -1 A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A -1 B.

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B.

Примеры. Решить системы уравнений.

Найдем матрицу обратную матрице A.

,

Таким образом, x = 3, y = – 1.

Решите матричное уравнение: XA+B=C, где

Выразим искомую матрицу X из заданного уравнения.

Найдем матрицу А -1 .

Решите матричное уравнение AX+B=C, где

Из уравнения получаем .

Следовательно,

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы.

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – на A₂₁ и 3-е – на A₃₁:

Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

.

Далее рассмотрим коэффициенты при x₂:

Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

Решите систему уравнений при различных значениях параметра p:

Система имеет единственное решение, если Δ ≠ 0.

. Поэтому .

1. При
2. При p = 30 получаем систему уравнений которая не имеет решений.
3. При p = –30 система принимает вид и, следовательно, имеет бесконечное множество решений x=y,y Î R.

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

.

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x₁. Для этого второе уравнение разделим на а₂₁ и умножим на –а₁₁, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а₃₁ и умножим на –а₁₁, а затем сложим с первым. В результате исходная система примет вид:

Теперь из последнего уравнения исключим слагаемое, содержащее x₂. Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x₃, затем из 2-го уравнения x₂ и, наконец, из 1-го – x₁.

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

1. перестановка строк или столбцов;
2. умножение строки на число, отличное от нуля;
3. прибавление к одной строке другие строки.

Примеры: Решить системы уравнений методом Гаусса.

Вернувшись к системе уравнений, будем иметь

Выпишем расширенную матрицу системы и сведем ее к треугольному виду.

Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.

Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.

Вернемся к системе уравнений.

Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.

Таким образом, система имеет бесконечное множество решений.

Симплекс-метод. Анализ чувствительности изменения коэффициентов целевой функции и запасов сырьевых ресурсов

Задача 29. Фирма «Television» производит два вида телевизоров: «Астро» и «Космо».

В цехе 1 производят телевизионные трубки. На производство одной трубки к телевизору «Астро» требуется потратить 1,2 человекочаса, а на производство трубки к «Космо» — 1,8 человекочаса. В настоящее время в цехе 1 на производство трубок к обеим мар­кам телевизоров может быть затрачено не более 120 человекочасов в день.

В цехе 2 производят шасси с электронной схемой телевизора. На производство шасси для телевизора любой марки требуется затратить 1 человекочас. На производство шасси к обеим маркам телевизоров в цехе 2 может быть затрачено не более 90 человеко-часов в день.

Продажа каждого телевизора марки «Астро» обеспечивает при­быль в размере 1500 руб., а марки «Космо» — 2000 руб. Фирма заинтересована в максимизации прибыли.

а) Какова максимальная ежедневная прибыль компании.

b ) Произвести анализ чувствительности изменения коэффициентов целевой функции.

с) Произвести анализ чувствительности запасов сырьевых ресурсов.

d ) На сколько рублей в день увеличится прибыль, если ресурс времени в цехе 2 возрастет на 5 человеко/часов?

Сделать выводы и записать рекомендации по производству.

а) Какова максимальная ежедневная прибыль компании.

Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим максимальное значение целевой функции F(X) = 1500x₁+2000x₂ при следующих условиях-ограничений.
x₁+x₂≤90
1.2x₁+1.8x₂≤120
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
В 1-м неравенстве смысла (≤) вводим базисную переменную x₃. В 2-м неравенстве смысла (≤) вводим базисную переменную x₄.
x₁+x₂+x₃ = 90
1.2x₁+1.8x₂+x₄ = 120
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:

Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.
Решим систему уравнений относительно базисных переменных: x₃, x₄
Полагая, что свободные переменные равны 0, получим первый опорный план:
X0 = (0,0,90,120)
Базисное решение называется допустимым, если оно неотрицательно.

Переходим к основному алгоритму симплекс-метода.
Итерация №0 .
1. Проверка критерия оптимальности .
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
2. Определение новой базисной переменной .
В качестве ведущего выберем столбец, соответствующий переменной x₂, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной .
Вычислим значения D_i по строкам как частное от деления: b_i / a_i2
и из них выберем наименьшее:
min (90 : 1 , 120 : 1.8 ) = 66.667
Следовательно, 2-ая строка является ведущей.
Разрешающий элемент равен (1.8) и находится на пересечении ведущего столбца и ведущей строки.

4. Пересчет симплекс-таблицы .
Формируем следующую часть симплексной таблицы. Вместо переменной x₄ в план 1 войдет переменная x₂.
Строка, соответствующая переменной x₂ в плане 1, получена в результате деления всех элементов строки x₄ плана 0 на разрешающий элемент РЭ=1.8. На месте разрешающего элемента получаем 1. В остальных клетках столбца x₂ записываем нули.
Таким образом, в новом плане 1 заполнены строка x₂ и столбец x₂. Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника.
Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ — (А*В)/РЭ
СТЭ — элемент старого плана, РЭ — разрешающий элемент (1.8), А и В — элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:

Получаем новую симплекс-таблицу:

Итерация №1 .
1. Проверка критерия оптимальности .
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
2. Определение новой базисной переменной .
В качестве ведущего выберем столбец, соответствующий переменной x₁, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной .
Вычислим значения D_i по строкам как частное от деления: b_i / a_i1
и из них выберем наименьшее:
min (23.333 : 0.333 , 66.667 : 0.667 ) = 70
Следовательно, 1-ая строка является ведущей.
Разрешающий элемент равен (0.333) и находится на пересечении ведущего столбца и ведущей строки.

4. Пересчет симплекс-таблицы .
Формируем следующую часть симплексной таблицы. Вместо переменной x₃ в план 2 войдет переменная x₁.
Строка, соответствующая переменной x₁ в плане 2, получена в результате деления всех элементов строки x₃ плана 1 на разрешающий элемент РЭ=0.333. На месте разрешающего элемента получаем 1. В остальных клетках столбца x₁ записываем нули.
Таким образом, в новом плане 2 заполнены строка x₁ и столбец x₁. Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника.
Представим расчет каждого элемента в виде таблицы:

Получаем новую симплекс-таблицу:

1. Проверка критерия оптимальности .
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
Окончательный вариант симплекс-таблицы:

Оптимальный план можно записать так:
x₁ = 70, x₂ = 20
F(X) = 1500*70 + 2000*20 = 145000
Анализ оптимального плана .
Значение 0 в столбце x₁ означает, что использование x₁ — выгодно.
Значение 0 в столбце x₂ означает, что использование x₂ — выгодно.
Значение 500 в столбце x₃ означает, что теневая цена (двойственная оценка) равна y₁=500.
Значение 833.333 в столбце x₄ означает, что теневая цена (двойственная оценка) равна y₂=833.333.

b ) Произвести анализ чувствительности изменения коэффициентов целевой функции.

Изменение значений коэффициентов c₁ и c₂ приводит к изменению угла наклона прямой z. Существует интервалы изменения коэффициентов c₁ и c₂, когда текущее оптимальное решение сохраняется. Задача анализа чувствительности и состоит в получении такой информации. Необходимо определить интервал оптимальности для отношения c₁ / c₂ (или c₂ и c₁). Если значение отношения c₁ / c₂ не выходит за пределы этого интервала, то оптимальное решение в данной модели сохраняется неизменным.
Таким образом, в рамках анализа на чувствительность к изменениям коэффициентов целевой функции могут исследоваться вопросы:

1. Каков диапазон изменения того или иного коэффициента целевой функции, при котором не происходит изменения оптимального решения.

2. На сколько следует изменить тот или иной коэффициент целевой функции, чтобы изменить статус некоторого ресурса.

На предыдущем рисунке видно, что функция достигает своего оптимума в точке, которая является пересечением прямых (x₁+x₂=90) и (1.2x₁+1.8x₂=120). При изменении коэффициентов целевой функции эта точка останется точкой оптимального решения до тех пор, пока угол наклона линии z будет лежать между углами наклона этих прямых. Алгебраически это можно записать следующим образом:

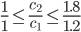
при условии c₁ ≠ 0

или

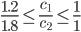
при условии c₂ ≠ 0

Таким образом, мы получили две системы неравенств, определяющих интервал оптимальности.

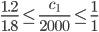
или
1333.33 ≤ c₁ ≤ 2000

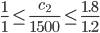
или
1500 ≤ c₂ ≤ 2250

Чувствительность решения к изменению коэффициентов целевой функции .

Так как любые изменения коэффициентов целевой функции оказывают влияние на оптимальность полученного ранее решения, то наша цель — найти такие диапазоны изменения коэффициентов в целевой функции (рассматривая каждый из коэффициентов отдельно), при которых оптимальные значения переменных остаются неизменными.
Пусть каждое значение параметра целевой функции изменится на ∆ с_i. Найдем интервалы, при которых будет экономически выгодно использование ресурсов.

Допустимые диапазоны изменения коэффициентов в целевой функции определятся из соотношений:

Анализ оптимального решения на чувствительность к изменениям исходных условий (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

1.4. Анализ оптимального решения на чувствительность

к изменениям исходных условий

Анализ моделей на чувствительность позволяет выявить чувствительность оптимального решения к определенным изменениям исходных условий, например:

1) изменениям запасов исходных продуктов,

2) изменениям рыночного спроса на изделия,

3) изменениям рыночных цен на изделия.

Каждое ограничение задачи линейного программирования представляется прямой, соответствующей уравнению ограничений линейной модели. В нашем примере (см. задачу в п.1.3) это прямые (рис. 1.12):

при ограничениях

1

2

3

4

5

6

Дефицитным ограничением называется то, для которого прямая, соответствующая ограничению, проходит через оптимальную точку. В этом случае выражение ограничения используется как уравнение, т. е. описываемое им условие выполняется на пределе. В нашем примере это прямые и

В противном случае ограничение относится к разряду недефицитных, т. е. выполняющихся с запасом. В нашем примере это прямые

Изменению ограничения соответствует изменение правой части неравенства. Изменение значения правой части неравенства выражается параллельным перемещением отображающей его прямой.

1.4.1. Улучшение оптимального решения за счет

изменения дефицитного ограничения

Увеличение недефицитных (избыточных) ресурсов не приводит к изменению оптимального значения целевой функции. Рассмотрим увеличение дефицитных ресурсов.

Ресурс (запас исходного продукта ) соответствует прямой . При его увеличении прямая перемещается вверх параллельно самой себе.

Пределом увеличения ресурса является точка пересечения прямых и т. к. в этой точке ресурс еще остается дефицитным, а его дальнейшее увеличение переводит его в разряд недефицитных и это ограничение уже не влияет на оптимальное решение. Оптимальная точка теперь лежит не пересечении прямых и , которые соответствуют дефицитным ограничениям. Координаты этой точки могут быть рассчитаны из системы уравнений (2) и (4):

Таким образом, суточный запас исходного продукта можно увеличить до тонн:

Это приведет к увеличению оптимального значения целевой функции, т. е. максимального суточного дохода фирмы до тыс. у. е.:

Аналогично можно увеличивать ресурс :

Суточный запас исходного продукта можно увеличить до тонн:

Это приведет к увеличению оптимального значения целевой функции до тыс. у. е.:

1.4.2. Изменение недефицитного ограничения

без изменения оптимального решения

Сокращение дефицитного ресурса не улучшает значения целевой функции. Поэтому будем рассматривать уменьшение недефицитных ресурсов.

Перемещение прямых, соответствующих недефицитным ограничениям, можно осуществлять до их пересечения с оптимальной точкой , после чего они становятся дефицитными.

Прямую можно спускать вниз до пересечения с оптимальной точкой без изменения оптимального решения. Это соответствует уменьшению предельного уровня спроса на изделие 1-ого вида до величины

Прямую можно двигать вправо до пересечения с оптимальной точкой. Это соответствует тому, что ранее полученное оптимальное решение не изменится, если спрос на изделие 2-ого вида превысит спрос на изделие 1-ого вида не менее, чем на :

1.4.3. Степень чувствительности оптимального решения

к изменениям дефицитных ограничений

По результатам предыдущего анализа известны пределы увеличения дефи­цитных ресурсов и приращения дохода за счет этого. Можно найти величину ценности единицы -ого дефицитного ресурса из соотношения:

Для дефицитных ограничений и :

,

.

Полученные результаты свидетельствуют о том, что дополнительные вло­жения выгоднее направить на увеличение ресурса .

1.4.4. Пределы изменения коэффициентов целевой функции

без изменения оптимального решения

Цены реализации изделий представляются коэффициентами целевой функ­ции, которые определяют наклон прямой, отображающей эту функцию в приня­той системе координат.

Обозначим цену изделия 1-ого вида через , 2-ого вида – через . Тогда целевая функция представляется следующим образом:

Можно показать, как вращается вокруг оптимальной точки прямая, отобра­жающая целевую функцию .

Оптимальная точка не изменится до тех пор, пока наклон прямой не выйдет за пределы, определяемые наклонами прямых для ограничений и , т. е.

Вопросы для самопроверки

¨ К каким изменениям исходных условий позволяет выявить чувствительность оптимального решения анализ модели задачи линейного программирования на чувствительность?

¨ Какое ограничение задачи линейного программирования называется дефицитным?

¨ За счет изменения каких ограничений осуществляется улучшение оптимального решения задачи линейного программирования?

¨ До какого предела может изменяться дефицитное ограничение?

¨ До какого предела может изменяться недефицитное ограничение?

¨ Как определяется степень чувствительности оптимального решения к изменениям дефицитных ограничений?

¨ В каких пределах могут изменяться коэффициенты целевой функции без изменения оптимального решения?

Задания для самостоятельной работы

Использовать графическое решение задачи линейного программирования:

,

,

,

.

В ответе указать:

1) номера ограничений, являющихся дефицитными;

2) номер дефицитного ограничения, увеличение которого приводит к наибольшему увеличению целевой функции.

Рассмотрим графическое решение задачи.

Оптимальное решение соответствует опорной точке с координатами , являющейся пересечением прямых и . Следовательно, соответствующие этим прямым ограничения и являются дефицитными, т. к. они выполняются на пределе, т. е. выполняются как уравнения:

.

Увеличение дефицитных ограничений приводит к увеличению оптимального значения целевой функции.

Графически увеличение ограничения выражается перемещением прямой параллельно самой себе вверх по оси .

Пределом увеличения ограничения является точка пересечения прямых и , т. к. в этой точке с координатами ограничение становится недефицитным и его дальнейшее увеличение не влияет на оптимальное решение.

Рассчитаем величину целевой функции в этой точке:

.

Графически увеличение дефицитного ограничения выражается перемещением прямой параллельно самой себе до точки пересечения прямых и с координатами , соответствующими решению системы уравнений:

В указанной точке ограничение становится недефицитным и его дальнейшее увеличение не влияет на оптимальное решение.

Величина целевой функции рассчитывается:

.

Следовательно, сравнивая возможности увеличения значения целевой функции за счет увеличения дефицитных ограничений, приходим к выводу, что увеличение ограничения влечет наибольшее увеличение целевой функции.

Для анализа оптимального решения на чувствительность к изменениям ограничений использовать графическое решение задач линейного программирования 1÷32 из предыдущего задания в п. 2.3.

В ответе указать:

1) номера ограничений, являющихся дефицитными;

2) номер дефицитного ограничения, увеличение которого приводит к наибольшему увеличению целевой функции.

1.5. Каноническая форма представления области решений

задачи линейного программирования

Учитывая, что множество точек, удовлетворяющих уравнению

при является прямой, при — плоскостью, а при — ее обобщением в -мерном векторном пространстве — гиперплоскостью, сделанные ранее выводы по результатам изучения области решений задачи линейного программирования в двумерном пространстве можно распространить на случай трех и более переменных. Тогда множество всех решений линейного неравенства с переменными

является одним из полупространств, на которые все пространство делится гиперплоскостью

включая и эту гиперплоскость. Далее область решений задачи линейного программирования определяется как пересечение всех полупространств, каждое из которых соответствует каждому линейному неравенству из входящих в ограничения этой задачи. Отсюда множество решений совместной системы линейных неравенств с переменными

является выпуклым многогранником (выпуклой многогранной областью) в -мерном векторном пространстве.

Обобщением понятия отрезка для точек является их выпуклая линейная комбинация: точка (вектор) называется выпуклой линейной комбинацией точек (векторов) если выполняются условия

Можно доказать, что выпуклый -мерный многогранник является выпуклой линейной комбинацией своих угловых точек. Отсюда следует, что выпуклый многогранник, т. е. область решений задачи линейного программирования, порождается своими угловыми точками. Поэтому главное внимание при решении систем линейных неравенств, соответствующих многогранникам (многогранным областям) решений задач линейного программирования, должно быть уделено нахождению координат угловых точек.

Рассмотрим общий вид системы линейных неравенств

с дополнительными ограничениями

,.

и .

Можно доказать, что всякому решению

соответствует определенное решение

,

,

и наоборот, каждому решению

соответствует определенное решение

.

Используя это утверждение, представим рассматриваемую систему линейных неравенств в каноническом виде, т. е. в виде эквивалентной системы линейных уравнений:

Любую систему линейных неравенств с дополнительными ограничениями неотрицательности переменных можно представить в каноническом виде. Так, в рассматриваемой системе все неравенства вида ««, поэтому дополнительные неотрицательные переменные вводились со знаком»«. Неравенства вида «» могут быть приведены к виду «» (умножением правой и левой частей на ««), что равносильно вводу со знаком «» дополнительных неотрицательных переменных для неравенств вида ««.

Считая, что в полученной системе линейных уравнений (системе линейных неравенств в каноническом виде) все уравнений независимы, т. е. ранг матрицы системы меньше числа переменных, любые переменных назовем базисными, если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные переменных называются свободными.

Базисными могут быть разные группы из переменных. Максимально возможное число групп базисных переменных равно числу способов выбора переменных из их общего числа т. е. числу сочетаний Но так как могут встретиться случаи, когда определитель матрицы коэффициентов при переменных равен нулю, то общее число групп базисных переменных не превосходит .

Оставим в левых частях уравнений полученной системы (системы линейных неравенств в каноническом виде) члены с переменными

а члены с переменными

перенесем в правые части. Получим:

Задавая свободным переменным

произвольные значения, каждый раз будем получать новое решение. Следовательно, полученная система линейных уравнений (система линейных неравенств в каноническом виде) будет иметь бесконечное множество решений.

Если и свободные переменные приравнять нулю, то получаем первоначальный план, которым называется начальное решение задачи линейного программирования, так как соответствующая ему точка является угловой точкой, или опорным планом. Тогда для отыскания оптимального плана (решения) необходимо исследовать только опорные планы. Поэтому требуется иметь схему, позволяющую осуществить упорядоченный переход от одного опорного плана к другому. Такой схемой является симплекс-метод, который позволяет, исходя из известного (начального) опорного плана задачи, за конечное число шагов получить ее оптимальный план. Каждый из шагов (или итераций) состоит в нахождении нового плана по предыдущему. Причем новому плану соответствует большее (при максимизации) или меньшее (при минимизации) значение линейной целевой функции, чем значение этой же функции в предыдущем плане. Процесс продолжается до получения оптимального плана или до установления неограниченности целевой функции на многограннике решений (за конечное число шагов-итераций).

Вопросы для самопроверки

¨ Можно ли распространить на случай трех и более переменных выводы по результатам изучения области решений задачи линейного программирования в двумерном пространстве?

¨ Как представляется система линейных неравенств в каноническом виде?

¨ Какую систему линейных неравенств нельзя представить в каноническом виде?

¨ Как с помощью базисных и свободных переменных находится каждое из множества решений задачи линейного программирования?

¨ При каком условии найденное решение задачи линейного программирования будет опорным планом?

¨ Почему для отыскания оптимального плана (решения) необходимо исследовать только опорные планы?

¨ Какую схему, позволяющую осуществить упорядоченный переход от одного опорного плана к другому, называют симплекс-методом?

¨ Что получается в результате каждого шага (итерации) симплекс-метода?

1.6. Решение задачи линейного программирования

Симплексный метод реализует направленный на оптимизацию значения целевой функции перебор опорных точек области ограничений задачи линейного программирования.

Итерацией называется переход от одной опорной точки к другой путем перехода от одного базиса к другому.

В симметричной форме задача линейного программирования имеет вид:

Каноническая форма задачи линейного программирования эквивалентна и используется для применения симплексного метода:

Для ограничений задачи линейного программирования в канонической форме легко выбрать исходное опорное решение: переменные при , коэффициенты при которых образуют единичную матрицу, равны свободным членам, а небазисные при

Имея исходное опорное решение, нужно проверить, является ли оно оптимальным. Если нет, то требуется перейти к другому опорному решению, оптимизирующему целевую функцию. Вычисления при переходе от одного базиса к другому удобно вести в симплексных таблицах (табл. 1.1).

Итерационный процесс максимизации плана путем замены некоторой базисной переменной на небазисную осуществляется следующими шагами.