Дан эллипс написать уравнение софокусной равнобочной гиперболы

Дан эллипс написать уравнение софокусной равнобочной гиперболы

Пусть теперь AB и CD — две взаимно перпендикулярные фокальные хорды эллипса или параболы. Тогда

Сумма обратных величин взаимно перпендикулярных фокальных хорд эллипса или параболы есть величина постоянная.

Софокусные конические сечения. Два центральных конических сечения (два эллипса, две гиперболы или эллипс и гипербола) называются софокусными, если они имеют общие фокусы. Две параболы называются софокусными, если они имеют общий фокус и их оси совпадают.

Два софокусных эллипса или две софокусные гиперболы не имеют общих точек, так как точкой и двумя фокусами эллипс или гипербола определяются однозначно. Софокусные эллипс и гипербола пересекаются в четырех точках (см. Рис. 3, а). Две софокусные параболы с сонаправленными осями не пересекаются.

Действительно, если бы они имели общую точку, то у них была бы общая директриса; но в таком случае параболы совпали бы, что противоречит условию. Две софокусные параболы с противоположно направленными осями пересекаются в двух точках (см. Рис. 3, б).

Равнобочная гипербола

Возьмем каноническое уравнение гиперболы

.

В случае, когда а=b, уравнение гиперболы имеет вид

х 2 — у 2 = а 2 . (6)

Гипербола, у которой полуоси а и b равны, называется равнобочной гиперболой. Уравнение (6) называется уравнением равнобочной гиперболы. Так как основной прямоугольник этой гиперболы является квадратом, то асимптоты равнобочной гиперболы будут перпендикулярны друг другу. (Рис. 5)

Сопряженная гипербола

. (7)

Представим уравнение (7) в следующем виде:

. (8)

Очевидно, что уравнение (8) представляет собой уравнение гиперболы, у которой действительной осью является ось ординат, а мнимой — ось абсцисс.

Построим основной прямоугольник, проведем асимптоты и построим гиперболу (7). Далее в той же системе координат построим (пунктиром) (Рис. 6) гиперболу

Очевидно, что гиперболы и имеют общие асимптоты. Такие гиперболы называются сопряженными.

Выведем теперь уравнение гиперболы, асимптотами которой служат оси координат. Возьмем уравнение равнобочной гиперболы х 2 — у 2 = а 2 и рассмотрим уравнение этой гиперболы в новой системе координат Х`OY`, полученной из старой поворотом осей координат на угол a= (Рис. 2).

Используя для этого формулы поворота осей координат:

х = х`cosa — y`sina;

y = x`sina + y`cosa,

подставим значения х, у в уравнение гиперболы:

. (9)

Обозначая , получим х`y`=c.

Уравнение равнобочной гиперболы, для которой координатные оси ОХ и OY являются асимптотами, будет иметь вид:

.

Математический портал

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Линейная алгебра
• Высшая математика.
• Аналитическая геометрия.
• Уравнение эллипса, гиперболы, параболы в полярной системе координат.

Уравнение эллипса, гиперболы, параболы в полярной системе координат.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Пример.

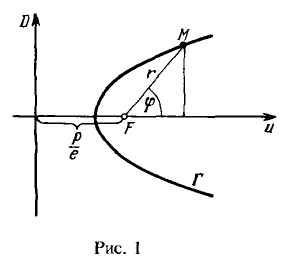
Пусть $\Gamma -$ эллипс, ветвь гиперболы или парабола, $F -$ фокус этой кривой, $D -$ соответствующая директриса. Вывести уравнение кривой $\Gamma$ в полярной системе координат, полюс которой совпадает с фокусом а полярная ось сонаправлена с осью кривой (см рисунок 1).

Решение.

Общее свойство эллипса, гиперболы и параболы состоит в следующем $$M\in\Gamma\Leftrightarrow\frac<\rho(M, F)><\rho(M, D)>=const=e,\qquad\qquad (1)$$ где $e -$ эксцентриситет кривой ( $e 1$ для гиперболы и $e=1$ для параболы)

Обозначим расстояние от фокусы до директрисы через $\frac

$( $p-$ параметр кривой, называемый полуфокальным параметром). Тогда из рисунка 1 следует, что $\rho(M, F)=r$ и $\rho(M, D)=\frac

+r\cos\varphi.$ Подставляя эти выражения в (1), получаем $$\frac<\frac

+r\cos\varphi>=e,$$ откуда $$r=\frac

<1-e\cos\varphi>.\qquad\qquad (2)$$ Уравнение (2) и есть искомое уравнение в полярной системе координат, общее для эллипса, гиперболы и параболы.

Примеры.

2.321(а).

Для эллипса $\frac<25>+\frac<16>=1$ написать полярное уравнение, считая, что полярная ось сонаправлена с осью абсцисс, а полюс находится в левом фокусе.

Решение.

Найдем эксцентриситет параболы и параметр $p:$

Далее, подставляя найденные параметры в полярное уравнение (2), найденное в предыдущей задаче, найдем уравнение данного эллипса:

2.324(а).

Написать каноническое уравнение кривой второго порядка $r=\frac<9><5-4\cos\varphi>.$

Решение.

Приведем заданное уравнение, к уравнению вида $r=\frac

<1-e\cos\varphi>:$

Отсюда имеем: $e=\frac<4><5>,$ $p=\frac<9><5>.$ Поскольку $e

Далее, подставляя выражения эксцентриситета и параметра по определению, надем полуоси эллипса:

Таким образом, запишем каноническое уравнение эллипса:

Вывести полярное уравнение гиперболы $\frac-\frac=1,$ при условии, что полярная ось сонаправлена с осью $Ox,$ а полюс находится в центре гиперболы.

Решение.

Так как полюс находится в центре гиперболы, то $OM=r,$ тогда $\rho(M, D)=r\cos\varphi-\frac,$ $\rho(M, F)=\sqrt <(r\sin\varphi)^2+(c-r\cos\varphi)^2>.$

Таким образом, из уравнения (1) находим:

Домашнее задание.

2.321(б) Для эллипса $\frac<25>+\frac<16>=1$ написать полярное уравнение, считая, что полярная ось сонаправлена с осью абсцисс, а полюс находится в правом фокусе.

2.322. Для правой ветви гиперболы $\frac<16>-\frac<9>=1$ написать полярное уравнение, считая, что полярная ось сонаправлена с осью абсцисс, а полюс находится

а) в левом фокусе, б) в правом фокусе.

2.323. Для параболы $y^2=6x$ написать полярное уравнение, считая, что полярная ось сонаправлена с осью абсцисс, а полюс находится в фокусе параболы.

2.324 (б, в) Написать канонические уравнения следующих кривых второго порядка:

Ответ: а) $\frac<16>-\frac<9>=1,$ б) $y^2=6x.$

2.327. Вывести полярное уравнение параболы $y^2=2px$ при условии, что полярная ось сонаправленна с осью $Ox,$ а полюс находится в вершине параболы.