Дано положительное число а известно что уравнение

Математика 10 класс, школьный этап (1 этап), 2018-2019 учебный год

Содержание

Задача 1

Разрежьте правильный пятиугольник на пять равных треугольников и один правильный пятиугольник меньшего размера.

Решение. Проведём лучи из вершин пятиугольника под равными углами со смежными с ними сторонами, как на рисунке. Каждый луч доведём до пересечения со следующим лучом.

Критерии

0 б. Любое разрезание, не удовлетворяющее хотя бы одному из условий.

4 б. Любое разрезание, удовлетворяющее всем условиям.

Задача 2

Ответ: 1346.

Решение. Имеем

Критерии

1 б. Только правильный ответ без доказательства.

2 б. С помощью верных алгебраических выкладок удалось избавиться от сумм с многоточиями, но допущена арифметическая ошибка.

4 б. Любое полное верное решение.

Задача 3

Числа от 1 до 50 написаны на карточках. Можно ли разложить эти карточки в 11 мешков (чтобы в каждый мешок попала хотя бы одна карточка) так, чтобы в каждом мешке произведение чисел на карточках делилось на 9?

Ответ: нет.

Решение. Предположим противное: пусть карточки можно разложить по одиннадцати мешкам так, чтобы выполнялось условие.

Для того чтобы произведение чисел на карточках в некотором мешке делилось на 9, необходимо и достаточно, чтобы было выполнено одно из двух условий:

• среди чисел на карточках в этом мешке есть хотя бы одно, кратное 9;
• среди чисел на карточках в этом мешке есть хотя бы два, кратных 3.

Из чисел от 1 до 50 ровно пять кратны 9 (это числа 9, 18, 27, 36, 45). Значит, хотя бы шесть мешков не содержат чисел, кратных 9. Эти мешки должны содержать как минимум по два числа, кратных 3, но не кратных 9. Тогда всего чисел, кратных 3, но не кратных 9, должно быть не менее 12. Но в промежутке от 1 до 50 ровно 11 таких чисел (3, 6, 12, 15, 21, 24, 30, 33, 39, 42, 48). Противоречие.

Критерии

0 б. Только ответ без доказательства.

1 б. В работе присутствует наблюдение, что среди чисел в мешке должно быть одно, кратное 9, или два, кратных 3, но дальнейших продвижений нет.

3 б. Идейно верное решение, неправильно построенное логически. Приведём эскиз такой потенциальной работы: «Чисел, кратных 9, ровно 5, их кладём в 5 мешков; остальных чисел, кратных 3, ровно 11, кладём их в 5 мешков по два, и ещё одно число осталось. Итого 10 мешков, а надо 11. Значит, нельзя». Правильно логически построенное решение должно приводить к противоречию любой потенциально возможный способ разложить числа; неправильно построенное решение опирается на конкретный способ раскладывать карточки по мешкам, который по каким-то причинам кажется автору оптимальным.

4 б. Любое полное верное решение.

Задача 4

Квадрат ABCD вписан в окружность ω. На меньшей дуге CD окружности ω выбрана произвольная точка M. Внутри квадрата отмечены такие точки K и L, что KLMD — квадрат. Найдите ∠AKD.

Решение.

Докажем равенство треугольников DAK и DCM. Проверим, что выполнены условия первого признака равенства треугольников. Отрезки DA и DC равны как стороны квадрата ABCD, отрезки DK и DM равны как стороны квадрата KLMD. Далее, поскольку углы ADC и KDM исходных квадратов прямые, можно записать

Таким образом, треугольники DAK и DCM действительно равны. Следовательно, ∠AKD = ∠CMD. Но ∠CMD = 135°, так как он вписанный и опирается на дугу DABC окружности ω, а мера этой дуги равна 270°. Тогда ∠AKD = 135°, что и требовалось найти.

Критерии

0 б. Любое незаконченное или ошибочное счётное решение.

1 б. Только правильный ответ без доказательства.

1 б. В работе упомянуто возможное равенство треугольников DAK и DCM, но не доказано или неправильно доказано; дальнейших продвижений нет.

2 б. В работе упомянуто возможное равенство треугольников DAK и DCM, но не доказано или неправильно доказано; далее решение закончено и получен правильный ответ.

2 б. Доказано равенство треугольников DAK и DCM, но угол AKD не найден или вычислен ошибочно.

4 б. Любое полное верное решение.

Задача 5

Дано положительное число a. Известно, что уравнение x 3 + 1 = ax имеет ровно два положительных корня, и отношение большего из них к меньшему равно 2018. Уравнение x 3 + 1 = ax 2 также имеет ровно два положительных корня. Докажите, что отношение большего из них к меньшему также равно 2018.

Решение. Обозначим положительные корни уравнения x 3 +1 = ax через x₁ и x₂

Из формул видно, что 1/x₁ и 1/x₂ — положительные корни уравнения x 3 +1 = ax 2 .

По условию их ровно два, и надо найти отношение большего к меньшему. Ясно, что 1/x₂ 1/ x₁ : 1/ x₂ = x ₂ : x ₁ = 2018.

Критерии

2 б. В работе отмечен тот факт, что при делении первого уравнения из условия на x 3 и последующей замены 1/x → x первое уравнение переходит во второе, но никаких дальнейших продвижений нет.

3 б. В работе доказано, что второе уравнение имеет положительные корни 1/x₁ и 1/x₂ , но отношение большего к меньшему найдено ошибочно (к примеру, перепутаны больший и меньший).

4 б. Любое полное верное решение.

Задача 6

Пятачок и Винни-Пух решили съесть квадратную шоколадку 7 × 7.

Они поочерёдно по клеточкам выедают из неё кусочки: Пятачок — 1×1, ВинниПух — 2× 1 или 1× 2 (кусочки можно выедать не обязательно с краю). Первый ход делает Пятачок. Если перед ходом Винни-Пуха в шоколадке не осталось ни одного кусочка 2 × 1 или 1 × 2, то вся оставшаяся шоколадка достаётся Пятачку. Кто из друзей сможет съесть больше половины всей шоколадки вне зависимости от действий второго?

Ответ: Пятачок.

Решение. Раскрасим мысленно все клетки шоколадки в два цвета в шахматном порядке. Получится 24 чёрные клетки и 25 белых клеток.

Опишем явно одну из возможных стратегий Пятачка. На каждом ходу Пятачок будет выедать какую-нибудь чёрную клетку. Заметим, что Винни-Пух каждым своим ходом съедает ровно одну чёрную клетку (и ровно одну белую). Таким образом, после первых 12 пар ходов все чёрные клетки закончатся, Винни-Пух больше не сможет ходить и вся оставшаяся шоколадка достанется Пятачку. Всего за первые 12 своих ходов Винни-Пух съест не более 24 клеток, что меньше половины всей шоколадки, и больше он ничего не съест. Следовательно, Пятачок, придерживаясь приведённой стратегии, съест больше половины шоколадки.

Критерии

0 б. Только правильный ответ.

0 б. Дана стратегия Пятачка, которая работает только против одной или нескольких возможных стратегий Винни-Пуха. Обычно в таких работах необснованно полагают, что какие-то ходы Винни-Пуха «выгоднее» других, и рассматривают только «выгодные» ходы. Сюда же относятся работы с неполнотой перебора возможных действий Винни-Пуха.

1 б. В работе присутствует идея шахматной раскраски шоколадки, но дальнейших продвижений нет.

2 б. В работе описана правильная стратегия Пятачка, которая на самом деле работает против любых возможных действий Вини-Пуха, но обоснования нет вовсе или в обосновании рассматриваются только одна или нескольких возможных стратегий Винни-Пуха.

4 б. Любое полное верное решение. Типичное решение должно содержать описание стратегии Пятачка и обоснование, почему приведённая стратегия работает против любых возможных действий Винни-Пуха.

Дано положительное число а известно что уравнение

Первый тур (10 минут; каждая задача – 6 баллов).

1.1.Два автобуса ехали навстречу друг другу с постоянными скоростями. Первый выехал из Москвы в 11 часов утра и прибыл в Ярославль в 16 часов, а второй выехал из Ярославля в 12 часов и прибыл в Москву в 17 часов. В котором часу они встретились?

Ответ: в 14 часов.

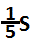
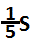
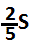
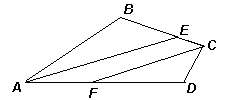
Решение. Так как каждый автобус ехал ровно 5 часов, то за час они проезжают одинаковые расстояния: , гдеS– длина пути от Москвы до Ярославля. К тому времени, как выехал второй автобус, первый успел проехать . После этого каждый автобус до встречи преодолел расстояние, равное . Следовательно, автобусы встретились через 2 часа после выезда второго, то есть в 14 часов.

Это рассуждение можно проиллюстрировать (см. рис. 1). 1.2.В четырёхугольнике ABCD биссектрисы АЕ и СF углов A и C параллельны (см. рисунок). Докажите, что углы B и D равны.

Решение. Из условия задачи и равенства соответственных углов при параллельных прямых следует, что ∠СFD = ∠EAD = ∠EAB и что ∠BEA = ∠BCF = ∠DCF (см. рис. 2). Тогда два угла треугольника АВЕ соответственно равны двум углам треугольника СDF. Следовательно, равны и третьи углы этих треугольников: ∠АВЕ = ∠СDF.

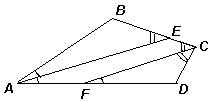
Можно также использовать свойства других углов при параллельных прямых и секущей.

1.3.Можно ли разрезать квадрат 5×5 на прямоугольники двух видов: 1×4 и 1×3 так, чтобы получилось 7 прямоугольников?

Решение. Например, см. рис. 3.

Отметим, что количество прямоугольников каждого вида определяется однозначно, а располагать их можно по-разному. Действительно,пусть x – количество прямоугольников 1× 4, тогда прямоугольников 1× 3 должно быть 7 – x.Уравнение 4x + 3(7 – x) = 25 имеет единственное решение: x = 4.

Второй тур (15 минут; каждая задача – 7 баллов).

2.1.Банк «Империал» при снятии денег со счета берет комиссию, состоящую из двух частей: фиксированной оплаты за проведение операции и еще оплаты, пропорциональной снятой сумме. Например, при снятии со счета 5000 рублей вкладчик заплатит 110 рублей, а при снятии 11000 рублей заплатит 230 рублей. Какую комиссию заплатит вкладчик, если он захочет снять со счета 8000 рублей?

Ответ: 170 рублей.

Решение. Пусть x рублей – фиксированная оплата, а k – коэффициент пропорциональности. Тогда в первом случае вкладчик заплатит x + 5000k рублей, а во втором случае – (x + 11000k) рублей. Следовательно, .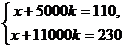

Решение этой системы: k= 0,02; x= 10. Значит, при снятии 8000 рублей вкладчик заплатит 10 + 8000·0,02 = 170 (р).

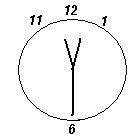
Ответ: 15° или 165°.

Решение. По прошествии часа минутная стрелка вернется в исходное положение, а часовая пройдет 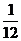ччасть окружности, то есть повернется на угол, равный 30°. Равенство углов, указанное в условии, означает, что минутная стрелка является либо биссектрисой угла между двумя положениями часовой стрелки (см., например, рис. 4а), либо лучом, дополнительным к этой биссектрисе (см., например, рис. 4б). В первом случае a = 30° : 2 = 15°, а во втором случае a = (360° – 30°) : 2 = 165°.

2.3.Известно, что остаток от деления некоторого простого числа на 60 равен составному числу. Какому?

Решение. Так как 60 = 2 2 ·3·5, то остаток не может быть кратен числам 2, 3 или 5 (иначе исходное число обладало бы тем же свойством и не могло бы оказаться простым). Так как остаток меньше, чем 60, и является произведением хотя бы двух простых множителей, то он равен 7·7 = 49. Другие варианты невозможны так как уже следующее произведение двух простых чисел: 7·11 > 60.

Ситуация, описанная в условии, возможна. Например, 109 = 60·1 + 49, где 109 – простое число.

Третий тур (15 минут; каждая задача – 7 баллов).

3.1.Девять чисел таковы, что сумма любых четырех из них меньше суммы пяти остальных. Докажите, что все числа положительные.

Решение. Разобьем данные числа на две группы: пять самых маленьких и четыре самых больших. Обозначим сумму чисел первой группы через А, а сумму чисел второй – через В, тогда, по условию А>B. Пусть какое-то из данных чисел x≤ 0, тогда оно из первой группы. Перенеся его во вторую группу, заметим, что от этого сумма А не уменьшилась, а сумма В – не увеличилась. Таким образом, знак неравенства не изменился, а это противоречит условию задачи. Следовательно, все данные числа положительные.

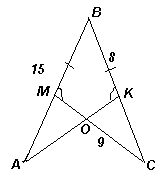
3.2.На сторонах угла ABC отмечены точки М и K так, что углы BMC и BKA равны, BM = BK, AB = 15, BK = 8, CM = 9. Найдите периметр треугольника СOK, где O – точка пересечения прямых AK и СМ.

Решение. У треугольников ABK и CBM – общий угол В, поэтому из условия задачи следует, что эти треугольники равны (по стороне и прилежащим углам, см. рис. 5). Тогда ∠BCM = ∠BAK и CB = AB = 15, значит, CK = AM = 7.

Учитывая также, что ∠CKO = ∠AMO (они дополняют равные углы до развернутых), получим, что ΔCOK = ΔAOM (по стороне и прилежащим углам). Следовательно, OK = OM. Таким образом, P_ΔCOK = CK + CO + OK = CK + CO + OM = CK + CM = 16.

3.3.В некоторой школе в каждом из 20 классов выбрали совет из 5 учеников. Петя оказался единственным мальчиком, избранным в совет класса вместе с четырьмя девочками. Он заметил, что еще в 15 классах девочек выбрали больше, чем мальчиков, хотя в целом по школе мальчиков и девочек выбрано поровну. Сколько мальчиков и сколько девочек в советах четырех оставшихся классов (в сумме)?

Ответ: 19 мальчиков и одна девочка.

Решение. Всего в советы было выбрано 5·20 = 100 человек. Девочек – половина, то есть 50. Если в классе было выбрано больше девочек, чем мальчиков, то девочек выбрано не менее трех. Значит, в 15 классах было выбрано не менее, чем 45 девочек. Еще 4 девочки было выбрано в Петином классе. Так как Петя – единственный мальчик, оказавшийся в совете вместе с четырьмя девочками, то больше ни в одном из классов не могли быть выбраны 4 девочки. Значит, в 16 классах выбрано ровно 49 девочек. Следовательно, в оставшихся четырех классах выбрали 19 мальчиков и одну девочку.

Четвертый тур (20 минут; каждая задача – 8 баллов).

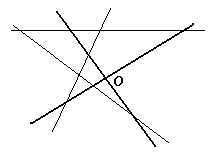
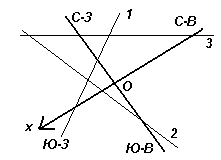
4.1.На листе бумаги были построены система координат (выделена жирно) и графики трех функций:y=ax + b,y=bx+cиy=cx+ a. После этого стерли обозначения и направления осей, а сам лист как-то повернули (см. рисунок). Укажите на рисунке ось абсцисс и ее направление.Ответ обоснуйте.

Решение.Первый способ. Так как графики попарно пересекаются, то среди чисел а, b и снет одинаковых. Кроме того, коэффициенты в уравнениях переставлены «по циклу», значит, без ограничения общности можно считать, что a 0,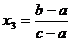 > 0. Выберем полуплоскость, ограниченную одной из осей, в которой располагаются ровно две точки пересечения графиков с положительными абсциссами. Из четырех полуплоскостей она определяется однозначно. Эта полуплоскость ограничена осью ординат и именно в ней лежит положительная полуось абсцисс.

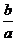
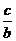
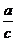
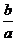
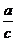
Второй способ. Пронумеруем графики функций, например, так: (1)y = ax + b, (2)y = bx + c, (3)y = cx + a(см. рис. 6). Допустим, что направление на северо-запад является положительным направлением оси ординат. Тогда точки пересечения графиков с этой осью имеют координаты (0; b), (0; c) и (0; а) соответственно, причем a > b > 0 > c. Точки пересечения графиков с другой осью имеют координаты (– ; 0), (– ; 0), (– ; 0), где – 0, – > 0. Отсюда следует, что направление на юго-запад – это положительное направление оси абсцисс, но это противоречит тому, что положительное направление оси абсцисс должно совмещаться с положительным направлением оси ординат поворотом вокруг начала координат против часовой стрелки.

Если же предположить, что положительное направление оси ординат – на юго-восток, то a 3 . Изменение любой цифры, кроме последней, а также замена последней цифры на любую цифру от 2 до 9 не дает простого числа по соображениям, изложенным выше. А если последнюю цифру заменить на 1, то получится число (10!) 3 + 1, которое можно разложить на множители по формуле суммы кубов: (10!) 3 + 1 = (10! + 1)((10!) 2 – 10! + 1). Значит, и в этом случае число не будет простым.

3) Рассмотрим число 19! + 10. Бесполезность изменения любой его цифры, кроме последней, уже объяснена выше, а замена последней цифры на 1, 2, . 9 приведет к тому, что полученные числа будут делиться на 11, 12, . 19 соответственно, то есть не будут простыми.

Дано положительное число а известно что уравнение

Покажем, как задачи с параметрами можно решать графически.

Найдём количество решений уравнения

в зависимости от $$ a$$.

Искомое количество решений совпадает с числом точек пересечения графиков функций

График первой функции получается из графика функции, который был построен в предыдущем примере. Для этого нужно воспользоваться преобразованием вида ПР1 то есть график $$ y=_<1>\left(x\right)$$ имеет такой вид, как показано на рис. 43 $$ f\left(0\right)=\sqrt<5>$$.

Графиком функции $$ y=a$$ будет прямая, параллельная оси $$ Ox$$ (рис. 43). При этом она пересекает ось ординат в точке $$ (0,a)$$. Легко видеть, что при $$a 3$$ прямая $$ y=a$$ не имеет пересечений с графиком $$ y=_<1>\left(x\right)$$, при $$ a=3$$ и $$ a\in [0;\sqrt<5>)$$ есть две точки пересечения, а при $$ a\in [\sqrt<5>;3)$$ – четыре общие точки и при $$ a=\sqrt<5>$$ – три общие точки. Остаётся лишь сформулировать ответ.

При $$ a\in (-\infty ;0)\bigcup (3;+\infty )$$ решений нет, при $$ a\in [0;\sqrt<5>)\bigcup \left\<3\right\>$$ – два решения, при $$ a\in \left\<\sqrt<5>\right\>$$ – три решения, при $$ a\in (\sqrt<5>;3)$$ – четыре решения.

Найдём количество решений уравнения в зависимости от $$ a$$:

Методом интервалов нетрудно построить график функции

Количество решений уравнения совпадает с числом точек пересечения этого графика с прямой $$ f\left(x\right)=a$$ (рис. 44).

Проанализировав график, несложно выписать ответ.

При $$ a\in (8;+\infty )$$ уравнение имеет 2 решения, при $$ a=8$$ уравнение имеет бесконечно много решений, при $$ a\in (-\infty ;8)$$ решений нет.

Рассмотрим ещё один пример задач с параметром, где используется построение множеств, задаваемых уравнениями с модулем. Напомним, что графиком уравнения называют линию на плоскости, на которой лежат те и только те точки, координаты которых удовлетворяют этому уравнению.

Найдём количество решений системы уравнений

в зависимости от $$ a$$.

Для решения необходимо построить график уравнения $$ \left|x\right|+\left|y\right|=4$$. Это можно сделать, последовательно выполнив построения таких графиков:

График второго уравнения – окружность с центром в точке $$ O(0;0)$$ и радиусом $$ \left|a\right|$$. Изобразим оба этих графика на координатной плоскости $$ xOy$$.

Как видим, при $$|a| 4$$ графики не пересекаются. При $$ \left|a\right|=2\sqrt<2>$$ или $$ \left|a\right|=4$$ есть 4 точки пересечения. При остальных $$ a$$ есть 8 точек пересечения. Таким образом, можно сформулировать ответ.

При $$ a\in (-\infty ;-4)\cup (-2\sqrt<2>;2\sqrt<2>)\cup (4;+\infty )$$ система не имеет решений;

при $$ a\in \<-4;-2\sqrt<2>;2\sqrt<2>;4\>$$ система имеет 4 решения;

при $$ a\in (-4;-2\sqrt<2>)\cup (2\sqrt<2>;4)$$ система имеет 8 решений.

В следующей задаче нам потребуется понятие локального экстремума функции. Говорят, что функция $$ y=f\left(x\right)$$ имеет локальный максимум в точке $$ _<0>$$, если для некоторого числа $$ε > 0$$ при $$|x − x_0| 0$$ при $$|x − x_0| 0$$ график $$ y=at-3$$ касается линии $$ y=\sqrt$$ (cм. рис. 46). Уравнение $$ D=0$$ имеет единственный положительный корень `a=1/4`. Следовательно, `a_2=1/4`. Если $$\dfrac3<16>\leq a 1/4` они не имеют общих точек.

Рассмотрим пример использования этого правила в задаче.

Найдём все значения параметра $$ a$$, при которых система

имеет хотя бы одно решение.

Неравенство системы после выделения полных квадратов можно записать в виде $$ ^<2>-8\left|x\right|+16+^<2>-8\left|y\right|+16\le 1$$ или $$ \left(\right|x|-4<)>^<2>+(\left|y\right|-4<)>^<2>\le 1$$. Множество $$ E$$ решений этого неравенства – объединение кругов $$ _<1>$$, $$ _<2>$$, $$ _<3>$$, $$ _<4>$$ (вместе с их границами) радиуса $$ 1$$ (см. рис. 47) с центрами $$ _<1>(4;4)$$, $$ _<2>(4;-4)$$, $$ _<3>(-4;-4)$$, $$ _<4>(-4;4)$$. Запишем уравнение системы в виде

Это уравнение задаёт окружность $$ L$$ радиуса $$ \left|a\right|$$ с центром в точке $$ M(0;1)$$, или точку $$ (0;1)$$ при $$ a=0$$. Исходная система имеет хотя бы одно решение при тех значениях $$ a$$, при которых окружность $$ L$$ имеет общие точки с множеством $$ E$$. При этом ввиду симметричного расположения соответствующих пар кругов относительно оси ординат достаточно выяснить, при каких значениях $$ a$$ окружность $$ L$$ имеет общие точки с кругами, центрами которых являются точки $$ _<1>$$ и $$ _<2>$$. Проведём из точки $$ M$$ лучи $$ _<1>$$ и $$ _<2>$$ в направлении точек $$ _<1>$$ и $$ _<2>$$. Пусть $$ _<1>$$ и $$ _<1>$$ – точки пересечения $$ _<1>$$ и окружности с центром $$ _<1>$$, $$ _<2>$$ и $$ _<2>$$ – точки пересечения $$ _<2>$$ и окружности с центром $$ _<2>$$. Тогда из геометрических соображений имеем:

При $$ 4\le \left|a\right|\le 6$$ окружность с центром $$ M$$ имеет общие точки с кругом $$ <\omega >_<1>$$ , а при $$ \sqrt<41>-1\le \left|a\right|\le \sqrt<41>+1$$ – с кругом $$ <\omega >_<2>$$.

а) Если $$b 0$$. Эта система не имеет решений при $$ a=0$$ и поэтому $$b 0$$. Теперь мы прибегнем к графическому методу. Рассмотрим два случая: $$0 1$$. Если $$b > 1$$, то $$\sqrt Эта система не имеет решений, так как прямая $$ y=x-b$$ не пересекает график функции $$ y=|^<2>-b|$$ (см. рис. 48). Если $$0 0$$).

В завершении разберём несколько задач с параметрами, которые удобно решать методом областей на координатной плоскости.

Найдём все значения `a`, при каждом из которых уравнение

Рассмотрим функции `f(x)-a|x-3|` и `g(x)=5/(x+2)`.

Если построить график функции `f(x)` для разных `a` (рис. 50) и график функции `g(x)` (рис. 51), то можно без проблем исследовать на промежутке `[0;+oo)` уравнение `f(x)=g(x)`.

При `a При `a>0` функция `f(x)` возрастает на промежутке `(3;+oo)`. Функция `g(x)` убывает на этом промежутке, поэтому уравнение `f(x)=g(x)` всегда имеет ровно одно решение на промежутке `(3;+oo)`, поскольку `f(3) g(3+1/a)`. На промежутке `[0;3]` уравнение `f(x)=g(x)` принимает вид `3a-ax=5/(x+2)`. Это уравнение сводится к уравнению `ax^2-ax+(5-6a)=0`. Будем считать, что `a>0`, поскольку случай `a

Пусть уравнение имеет два корня, то есть `a>4/5`. Тогда оба корня меньше `3`, поскольку при `x>=3` значения функции `3a-ax` неположительны, а значения функции `5/(x+2)` положительны. По теореме Виета сумма корней равна `1`, а произведение равно `5/6-6`. Значит, больший корень всегда принадлежит промежутку `[0;3]`, а меньший принадлежит этому промежутку тогда и только тогда, когда `5/a-6>=0`, то есть `a 5/6`;

– три корня при `4/5

В завершении разберём несколько задач с параметрами, которые удобно решать методом областей на координатной плоскости. В следующем примере будем использовать известный подход к задачам, содержащим некоторые переменные в квадрате. Суть этого подхода — рассмотрение выражения как квадратичной функции относительно какой-нибудь переменной (остальные переменные при этом считаются параметрами) с последующим использованием известных свойств квадратичной функции.

Найдём все значения параметра $$ a$$, при каждом из которых система уравнений

имеет ровно три решения.

Первое уравнение данной системы равносильно совокупности двух уравнений $$ |y+9|+|x+2|=2$$ и $$ ^<2>+^<2>=3$$. Первое из них задаёт квадрат $$ G$$ с центром $$ (-2;-9)$$, диагонали которого равны $$ 4$$ и параллельны осям координат. Второе задаёт окружность $$ S$$ с центром $$ (0;0)$$ радиуса $$ \sqrt<3>$$ (см. рис. 52).

Второе уравнение исходной системы при $$a > 0$$ задаёт окружность $$ \Omega $$ с центром $$ (-2;-4)$$ радиуса $$ R=\sqrt$$.

Отметим, что при $$a Рассмотрев случаи внешнего и внутреннего касания окружностей $$ \Omega $$ и $$ S$$, можно заключить, что они имеют ровно `1` общую точку при $$ R=\sqrt<20>\pm \sqrt<3>$$, ровно `2` общие точки при $$ R\in (\sqrt<20>-\sqrt<3>;\sqrt<20>+\sqrt<3>)$$ и ни одной общей точки при остальных $$ R$$. Поскольку центры окружности $$ \Omega $$ и квадрата $$ G$$ лежат на прямой $$ x=-2$$, то $$ \Omega $$ и $$ G$$ имеют ровно `1` общую точку при $$ R=3$$ или $$ R=7$$, ровно `2` общие точки при $$ R\in (3;7)$$ и ни одной общей точки при остальных значениях $$ R$$. Для того чтобы у системы было 3 решения, необходимо и достаточно, чтобы окружность $$ \Omega $$ имела `2` общие точки с квадратом $$ G$$ и `1` общую точку с окружностью $$ S$$ или наоборот. Рассмотрим значения $$ R$$, при которых окружность $$ \Omega $$ имеет с квадратом $$ G$$ или окружностью $$ S$$ ровно `1` общую точку.

1) $$ R=\sqrt<20>+\sqrt<3>$$. Тогда есть ровно `1` общая точка с окружностью $$ S$$, и ровно `2` общие точки с квадратом $$ G$$ (т. к. $$3 \sqrt <20>+ \sqrt<3>$$), т. е. у системы 1 решение.

Итак, подходят $$ R=3$$ и $$ R=\sqrt<20>+\sqrt<3>$$. Тогда искомые значения параметра $$ a=<3>^<2>=9$$ и $$ a=(\sqrt<20>+\sqrt<3><)>^<2>=23+4\sqrt<15>$$.