Дано уравнение линии f x y 0

Дано уравнение линии f x y 0

Глава 9. Понятие уравнения линии. Задание линии при помощи уравнения

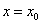
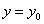
Равенство вида F(x; y )=0 называется уравнением с двумя переменными x, y , если оно справедливо не для всяких пар чисел x, y . Говорят, что два числа , удовлетворяют некоторому уравнению вида F(x, y )=0, если при подстановке этих чисел вместо переменных x и y в уравнение его левая часть обращается в нуль.

Уравнением данной линии (в назначенной системе координат) называется такое уравнение с двумя переменными, которому удовлетворяют координаты каждой точки, лежащей на этой линии, и не удовлетворяют координаты каждой точки, не лежащей на ней.

В дальнейшем вместо выражения «дано уравнение линии F(x; y )=0» мы часто будем говорить короче: «дана линия F(x; y)=0».

Если даны уравнения двух линий F(x,y )=0 и Ф( x, y )=0, то совместное решение системы F(x,y )=0, Ф( x, y )=0 дает все точки их пересечения. Точнее, каждая пара чисел, являющаяся совместным решением этой системы, определяет одну из точек пересечения.

Уравнение линии

Функция двух переменных

Если указано правило, согласно которому с каждой точкой М плоскости (или какой-нибудь части плоскости) сопоставляется некоторое число u, то говорят, что на плоскости (или на части плоскости) «задана функция точки»; задание функции символически выражается равенством вида u=f(M). Число u, сопоставляемое с точкой М, называется значением данной функции в точке М. Например, если А — фиксированная точка плоскости, М — произвольная точка, то расстояние от А до М есть функция точки М. В данном случае f(m)=AM.

Пусть дана некоторая функция u=f(M) и вместе с тем введена система координат. Тогда произвольная точка М определяется координатами x, y. Соответственно этому и значение данной функции в точке М определяется координатами x, y, или, как еще говорят, u=f(M) есть функция двух переменных x и y. Функция двух переменных x и y обозначается символом f(x; y): если f(M)=f(x;y), то формула u=f(x; y) называется выражением данной функции в выбранной системе координат. Так, в предыдущем примере f(M)=AM; если ввести декартову прямоугольную систему координат с началом в точке А, то получим выражение этой функции:

ЗАДАЧА 3688 Дана функция f (x, y)=x^2–y^2–16.

Понятие уравнения линии. Задание линии при помощи уравнения

Равенство вида F(x; y)=0 называется уравнением с двумя переменными x, y, если оно справедливо не для всяких пар чисел x, y. Говорят, что два числа x=x0, y=y0 удовлетворяют некоторому уравнению вида F(x, y)=0, если при подстановке этих чисел вместо переменных x и y в уравнение его левая часть обращается в нуль.

Уравнением данной линии (в назначенной системе координат) называется такое уравнение с двумя переменными, которому удовлетворяют координаты каждой точки, лежащей на этой линии, и не удовлетворяют координаты каждой точки, не лежащей на ней.

В дальнейшем вместо выражения «дано уравнение линии F(x; y)=0» мы часто будем говорить короче: «дана линия F(x; y)=0».

Если даны уравнения двух линий F(x,y)=0 и Ф(x, y)=0, то совместное решение системы F(x,y)=0, Ф(x, y)=0 дает все точки их пересечения. Точнее, каждая пара чисел, являющаяся совместным решением этой системы, определяет одну из точек пересечения.

ЗАДАЧА 3689 Даны линии. Определить, какие из них

Параметрические уравнения линии

Обозначим буквами х и у координаты некоторой точки М; рассмотрим две функции аргумента t:

При изменении t величины х и у будут, вообще говоря, меняться, следовательно, точка М будет перемещаться. Равенства (1) называются параметрическими уравнениями линии, которая является траекторией точки М; аргумент t носит название параметра. Если из равенств (1) можно исключить параметр t, то получим уравнение траектории точки М в виде

ЗАДАЧА 3690 Стержень АВ скользит своими концами А и

ЗАДАЧА 3691 Траекторией точки М является гипербола,

Уравнение прямой по точке и угловому коэффициенту

Глава 3

Аналитическая геометрия на плоскости

Аналитическая геометрия,раздел геометрии, который исследует простейшие геометрические объекты средствами элементарной алгебры на основе метода координат. Создание аналитической геометрии обычно приписывают Р.Декарту, изложившему ее основы в последней главе своего трактата Рассуждение о методе, озаглавленной Геометрия (1637).

Методы аналитической геометрии применимы к фигурам на плоскости и к поверхностям в трехмерном пространстве, а также допускают естественное обобщение и на пространства более высоких размерностей. Мы начнем с аналитической геометрии на плоскости.

Отрезок на координатной плоскости

Проекцией отрезка AB на ось Ox (Oy) называется отрезок [A_x; B_x] ([A_y; B_y]), где A_x и B_x(A_y, B_y) соответственно проекции точек A и B на ось Ox (Oy).

Если A₁ (x₁; y₁), A₂ (x₂; y₂) две произвольные точки плоскости Oxy, а d – расстояние между ними, то d вычисляется из соотношения d 2 = (x₁ – x₂) 2 + (y₁ – y₂) 2 _.

Если A(x₁; y₁), B(x₂; y₂) – произвольные разные точки плоскости Oxy, то координаты (x; y) середины отрезка AB вычисляют по формулам

Прямая на плоскости

2.1. Понятие уравнения линии

Пусть х и у — две произвольные переменные величины. Соотношение вида F(x, y) = 0, будем называть уравнением с двумя переменными х, у если F(x, у)=0 есть равенство, верное не всегда, т.е.не для всяких пар чисел х, у.

Говорят, что два числа х=х₀, у=y_о удовлетворяют некоторому уравнению с двумя переменными, если при подстановке их в это уравнение вместо переменных получается верное равенство.

Пусть на плоскости дана какая-нибудь линия и пусть вместе с тем выбрана некоторая система координат. Уравнением данной линии (в выбранной системе координат) называется такое уравнение F(x,y)=0 с двумя переменными, которому удовлетворяют координаты х и у каждой точки, лежащей на этой линии, и не удовлетворяют координаты никакой точки, не лежащей на ней.

Пересечение двух линий

Даны уравнения двух линий: F(x,y)= 0, Ф(х,у) = 0. Каждая точка пересечения данных линий есть их общая точка. Следовательно, координаты такой точки должны удовлетворять как уравнению F(x, у)=0, так и уравнению Ф (х, у) = 0. Каждое решение системы

определяет одну из искомых точек.

Общее уравнение прямой

Уравнением линии называется соотношение y = f(x) между координатами точек, составляющих эту линию.

Уравнение вида Аx + Вy + С = 0 где А, В, С – вещественные числа, при условии, что А и В одновременно не равны нулю, задает прямую в плоскости Oxy, и наоборот, уравнение произвольной прямой может быть записано в указанном виде. Это общее уравнение прямой.

В зависимости от значений постоянных А, В и С возможны следующие частные случаи:

а) А = 0, В ≠ 0. Уравнение определяет прямую, параллельную оси абсцисс и пересекающую ось ординат в точке с координатой

б) В = 0, А ≠ 0. Уравнение определяет прямую, параллельную оси ординат и пересекающую ось абсцисс в точке с координатой

в) С = 0. Уравнение определяет прямую, проходящую через начало координат.

Любой вектор параллельный прямой l, называется направляющим вектором этой прямой. Любой вектор перпендикулярный прямой l, называется нормальным вектором прямой. Если взять на прямой какие-либо две фиксированные точки М₀ и М₁ то вектор в частности, будет направляющим вектором прямой М₀ М₁

Для любой прямой, заданной общим уравнением Ax + By + C = 0, вектор перпендикулярен прямой, а вектор параллелен ей.

Пусть прямая проходит через точку М₀(х₀;у₀) параллельно вектору .

Уравнение называется каноническим уравнением прямой, с направляющим вектором

Уравнение прямой по точке и угловому коэффициенту

Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:

и обозначить , то полученное уравнение называется уравнением прямой с угловым коэффициентом k.

Число k называется угловым коэффициентом прямой и равно тангенсу угла между положительной полуосью абсцисс и лучом прямой, лежащей в одной с положительной полуосью ординат полуплоскости относительно оси абсцисс.

Условие параллельности прямых. Если две прямые параллельны, то их угловые коэффициенты равны.

Условие перпендикулярности прямых. Если две прямые перпендикулярны, то

Уравнение прямой, проходящей через данную точку в данном направлении.

Предположим, что прямая проходит через точку M₀ (x₀,y₀) и образует с осью OX угол j. Составим уравнение этой прямой.

Y

y – y₀ = k · (x – x₀) — уравнение прямой, проходящей через данную точку М₀ (х₀,у₀) в данном направлении.

Пример. Через точку М₀(1,-2) провести прямую ℓ параллельную прямой у = 2х — 1

Решение. Уравнение прямой ℓ запишем в виде у-у₀=К(х-х₀). Х₀ и у₀ – нам даны, это х₀=1, у₀=-2, К – угловой коэффициент найдем из условия параллельности двух прямых К=2. у+2=2(х — 1) – искомое уравнение или 2х – у — 4=0