Даны 4 точки составить уравнения плоскости прямой
Даны четыре точки A1( 5; 3; 7), A2 (-2; 3; 7), A3(4; 2; 10), A4(1; 2; 7).
а) плоскости А1А2А3;
Находим векторы А1А2 и А1А3.
А1А2 = (-2-5; 3-3; 7-7) = (-7; 0; 0).
А1А3 = (4-5; 2-3; 10-7) = (-1; -1; 3).
Нормальный вектор плоскости А1А2А3 находим из векторного произведения векторов А1А2 и А1А3.
-1 -1 3| -1 -1 = 0i + 0j + 7k + 21j + 0i + 0k =
Нормальный вектор плоскости А1А2А3 равен (0; 21; 7).
Подставляем найденные координаты нормального вектора в уравнение плоскости:
21y+7z−112=0 или после сокращения на 7:
Уравнение А1А2А3: 3y + z — 16.
Из этого уравнения можно принять нормальный вектор плоскости А1А2А3 равным (0; 3; 1).
Направляющий вектор найден выше: А1А2 = (-7; 0; 0).
Уравнение А1А2: (x — 5)/(-7) = (y — 3)/0 = (z — 7)/0.
Это уравнение прямой, параллельной оси абсцисс.
в) прямой А4М перпендикулярной к плоскости А1А2А3;
Направляющим вектором прямой А4М является нормальный вектор плоскости А1А2А3, найденный ранее и равный (0; 3; 1).
Уравнение А4М: (x — 1)/0 = (y — 2)/3 = (z — 7)/1.
г) прямой А3 N параллельной прямой А1А2.
У этой прямой направляющий вектор равен вектору А1А2,
Уравнение А3N: (x — 4)/(-7) = (y — 2)/0 = (z — 10)/0.
Это уравнение прямой, параллельной оси абсцисс.
д) плоскости проходящей через точку А4 перпендикулярно к прямой А1 А2.
У этой плоскости нормальный вектор совпадает с вектором А1А2.
после сокращения на -7 получаем
x – 1 = 0.
e) синус угла между прямой A1A4 и плоскостью A1A2A3.
= 21 = 0,23009
Угол равен 0,23217 радиан или 13,3023 градуса.
ж) косинус угла между координатной плоскостью Oxy и плоскостью A1A2A3.
Координатная плоскость Oxy имеет уравнение z = 0.
Уравнение плоскости А1А2А3: 3y + z — 16.
Вычислим угол между плоскостями
z = 0 и 3y + z – 16.
cos α = |A1·A2 + B1·B2 + C1·C2|/(√(A1² + B1² + C1²)* √(A2² + B2² + C2²)).
cos α = |0·0 + 0·3 + 1·1|/(√(0² + 0² + 1²)* √(0² + 3² + 1²)) =
= |0 + 0 + 1|/(√(0 + 0 + 1)* √(0 + 9 + 1)) =
= 1/√1* √10 = 1/√10 = √10/10 ≈ 0,3162.
Онлайн калькулятор. Уравнение плоскости
Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.
Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.
Найти уравнение плоскости
Выберите метод решения исходя из имеющихся в задаче данных:
В задаче известны:
Ввод данных в калькулятор для составления уравнения плоскости
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления уравнения плоскости
- Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.
Теория. Уравнение плоскости.
Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки
В зависимости от условий задачи уравнение плоскости можно составить следующими способами:
- Если заданы координаты трех точек A( x 1, y 1, z 1), B( x 2, y 2, z 2) и C( x 3, y 3, z 3), лежащих на плоскости, то уравнение плоскости можно составить по следующей формуле
| x — x 1 | y — y 1 | z — z 1 | = 0 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 | |
| x 3 — x 1 | y 3 — y 1 | z 3 — z 1 |
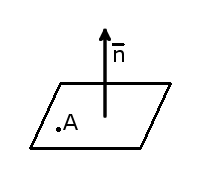
Если заданы координаты точки A( x 1, y 1, z 1) лежащей на плоскости и вектор нормали n =
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Уравнение плоскости, проходящей через точку и прямую онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и через данную прямую (точка не лежит на этой прямой). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через точку и прямую − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L:
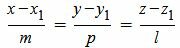 . . | (1) |
Задача заключается в построении уравнения плоскости α, проходящей через точку M0 и и через прямую L(Рис.1).
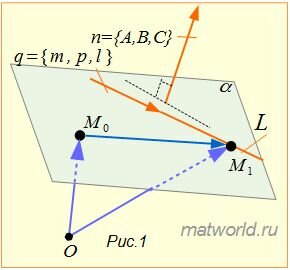 |
Решение. Уравнение плоскости, проходящей через точку M0 и имеющий нормальный вектор n=<A, B, C> имеет следующий вид:
| A(x−x0)+B(y−y0)+C(z−z0)=0. | (2) |
Направляющий вектор прямой L имеет вид q=<m, p, l>. Поскольку плоскость проходит через прямую L, то она проходит также через точку M1(x1, y1, z1). Тогда уравнение плоскости, проходящей через точку M1(x1, y1, z1) имеет вид:
| A(x−x1)+B(y−y1)+C(z−z1)=0. | (3) |
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:
Вычитая уравнение (3) из уравнения (2), получим:
| A(x1−x0)+B(y1−y0)+C(z1−z0)=0. | (5) |
Решая совместно уравнения (4) и (5) отностительно коэффициентов A, B, C получим такие значения A, B, C, при которых уравнение (2) проходит через точку M0 и через прямую (1). Для решения систему уравнений (4), (5), запишем их в матричном виде:
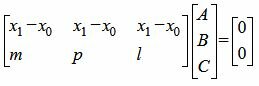 . . | (6) |
Как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн.
Получив частное решение уравнения (6) и подставив полученные значения A, B, C в (2), получим решение задачи.
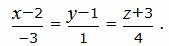 | (7) |
Решение. Уравнение плоскости α, проходящей через точку M0(x0, y0, z0)=M0(1, 2, 5) и имеющий нормальный вектор n=<A, B, C> представляется формулой (2).
Вычитая уравнение (3) из уравнения (2), получим:
| A(x1−x0)+B(y1−y0)+C(z1−z0)=0. | (8) |
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:
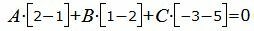 | (10) |
 | (11) |
Решим систему линейных уравнений (10) и (11) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:
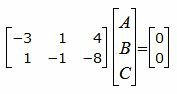 | (12) |
Решив однородную систему линейных уравнений (12) используя метод Гаусса, найдем следующее частное решение:
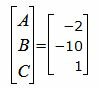 |
Подставляя значения коэффициентов A, B, C в уравнение плоскости (2), получим:
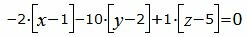 | (13) |
Упростим уравнение (13):
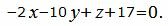 | (14) |
Ответ: Уравнение плоскости, проходящей через точку M0(1, 2, 5) и через прямую (7) имеет вид (14).
Пример 2. Найти уравнение плоскости α, проходящую через точку M0(4, 3, −6) и через прямую L, заданной параметрическим уравнением:
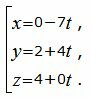 | (15) |
Решение. Приведем параметрическое уравнение (15) к каноническому виду:
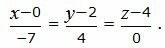 | (16) |
Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n=<A, B, C> представляется формулой:
| A(x−x0)+B(y−y0)+C(z−z0)=0. | (17) |
Поскольку плоскость проходит через прямую L, то она проходит также через точку M1(x1, y1, z1)=(0, 2, 4). Тогда уравнение плоскости, проходящей через точку M1(x1, y1, z1) имеет вид:
| A(x−x1)+B(y−y1)+C(z−z1)=0. | (18) |
Вычитая уравнение (18) из уравнения (17), получим:
| A(x1−x0)+B(y1−y0)+C(z1−z0)=0. | (19) |
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n должен быть ортогональным направляющему вектору прямой L :
| Am+Bp+Cl=0. | (20) |
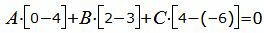 | (21) |
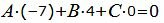 | (22) |
Решим систему линейных уравнений (21) и (22) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:
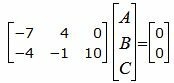 | (23) |
Решив однородную систему линейных уравнений (23) используя метод Гаусса, найдем следующее частное решение:
 |
Подставляя значения коэффициентов A, B, C в уравнение плоскости (17), получим:
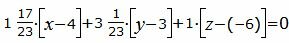 | (24) |
Упростим уравнение (24):
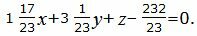 | (25) |
Уравнение плоскости можно представить более упрощенном виде, умножив на число 23.
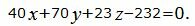 | (26) |
Ответ: Уравнение плоскости, проходящей через точку M0(4, 3, −6) и через прямую (16) имеет вид (26).
http://ru.onlinemschool.com/math/assistance/cartesian_coordinate/plane/
http://matworld.ru/analytic-geometry/uravnenie-ploskosti4-online.php