Даны четыре точки составить уравнения плоскости прямой
Даны четыре точки A1( 5; 3; 7), A2 (-2; 3; 7), A3(4; 2; 10), A4(1; 2; 7).
а) плоскости А1А2А3;
Находим векторы А1А2 и А1А3.
А1А2 = (-2-5; 3-3; 7-7) = (-7; 0; 0).
А1А3 = (4-5; 2-3; 10-7) = (-1; -1; 3).
Нормальный вектор плоскости А1А2А3 находим из векторного произведения векторов А1А2 и А1А3.
-1 -1 3| -1 -1 = 0i + 0j + 7k + 21j + 0i + 0k =
Нормальный вектор плоскости А1А2А3 равен (0; 21; 7).
Подставляем найденные координаты нормального вектора в уравнение плоскости:
21y+7z−112=0 или после сокращения на 7:
Уравнение А1А2А3: 3y + z — 16.
Из этого уравнения можно принять нормальный вектор плоскости А1А2А3 равным (0; 3; 1).
Направляющий вектор найден выше: А1А2 = (-7; 0; 0).
Уравнение А1А2: (x — 5)/(-7) = (y — 3)/0 = (z — 7)/0.
Это уравнение прямой, параллельной оси абсцисс.
в) прямой А4М перпендикулярной к плоскости А1А2А3;
Направляющим вектором прямой А4М является нормальный вектор плоскости А1А2А3, найденный ранее и равный (0; 3; 1).
Уравнение А4М: (x — 1)/0 = (y — 2)/3 = (z — 7)/1.
г) прямой А3 N параллельной прямой А1А2.
У этой прямой направляющий вектор равен вектору А1А2,
Уравнение А3N: (x — 4)/(-7) = (y — 2)/0 = (z — 10)/0.
Это уравнение прямой, параллельной оси абсцисс.
д) плоскости проходящей через точку А4 перпендикулярно к прямой А1 А2.
У этой плоскости нормальный вектор совпадает с вектором А1А2.
после сокращения на -7 получаем
x – 1 = 0.
e) синус угла между прямой A1A4 и плоскостью A1A2A3.
= 21 = 0,23009
Угол равен 0,23217 радиан или 13,3023 градуса.
ж) косинус угла между координатной плоскостью Oxy и плоскостью A1A2A3.
Координатная плоскость Oxy имеет уравнение z = 0.
Уравнение плоскости А1А2А3: 3y + z — 16.
Вычислим угол между плоскостями
z = 0 и 3y + z – 16.
cos α = |A1·A2 + B1·B2 + C1·C2|/(√(A1² + B1² + C1²)* √(A2² + B2² + C2²)).
cos α = |0·0 + 0·3 + 1·1|/(√(0² + 0² + 1²)* √(0² + 3² + 1²)) =
= |0 + 0 + 1|/(√(0 + 0 + 1)* √(0 + 9 + 1)) =
= 1/√1* √10 = 1/√10 = √10/10 ≈ 0,3162.
Онлайн калькулятор. Уравнение плоскости
Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.
Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.
Найти уравнение плоскости
Выберите метод решения исходя из имеющихся в задаче данных:
В задаче известны:
Ввод данных в калькулятор для составления уравнения плоскости
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления уравнения плоскости
- Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.
Теория. Уравнение плоскости.
Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки
В зависимости от условий задачи уравнение плоскости можно составить следующими способами:
- Если заданы координаты трех точек A( x 1, y 1, z 1), B( x 2, y 2, z 2) и C( x 3, y 3, z 3), лежащих на плоскости, то уравнение плоскости можно составить по следующей формуле
| x — x 1 | y — y 1 | z — z 1 | = 0 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 | |
| x 3 — x 1 | y 3 — y 1 | z 3 — z 1 |
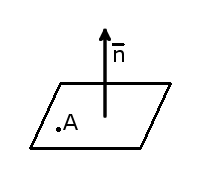
Если заданы координаты точки A( x 1, y 1, z 1) лежащей на плоскости и вектор нормали n =
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
4.2.10. Примеры решения задач по теме «Уравнение плоскости в пространстве»
Составить уравнение плоскости, проходящей через точки А=<5; -1; 3>,
Для того, чтобы составить уравнение плоскости, нужно знать координаты
Точки, лежащей в этой плоскости, и координаты нормали, то есть вектора, перпендикулярного плоскости.
Векторы АВ = (-3; 3; -3) и АС = (-6; 2; -2) параллельны данной плоскости, поэтому их векторное произведение или любой вектор, коллинеарный ему, является нормалью к плоскости.
Выберем в качестве нормали П = (0; 1; 1), а точкой <Х0; У0; Z0> будем считать точку В. Тогда уравнение плоскости имеет вид:
Составить канонические уравнения прямой
Для того, чтобы составить канонические или параметрические уравнения прямой в пространстве, нужно знать координаты какой-либо точки, лежащей на этой на этой прямой, и координаты направляющего вектора, то есть вектора, коллинеарного прямой.
Прямая является линией пересечения двух плоскостей, поэтому ее направляющий вектор А параллелен каждой из этих плоскостей и соответственно перпендикулярен нормалям П1 и П2 к данным плоскостям. В таком случае он коллинеарен векторному произведению [N1, N2].
Будем искать точку, лежащую на данной прямой, у которой одна из координат принимает выбранное нами значение; тогда остальные две координаты можно определить единственным образом из системы уравнений, задающей пересекающиеся плоскости. Выберем для удобства вычислений Z0 = 0, тогда для точки М=<Х0; У0; 0>
Теперь составим канонические уравнения данной прямой:
Ответ:
Составить уравнение плоскости, проходящей через прямую L:
Точка А= <-3,5,-1>принадлежит плоскости, соответственно вектор 
Поскольку прямая лежит в плоскости, ее направляющий вектор A = (2: 1: -1) параллелен плоскости. При T = 0 из уравнений прямой получаем:
Координаты точки А, принадлежащей прямой и соОтВетственно плоскости.
Тогда вектор АМ = (5; -8; 2) параллелен Плоскости. Следовательно, нормаль
П к плоскости коллинеарна векторному произведению [A, AM] = (-6; -9; — 21).
Выберем N = (2; 3; 7) и составим уравнение плоскости, проходящей через
Найти кратчайшее расстояние между прямыми
Координаты направляющих векторов данных прямых A1 = <3; 2; -2>и
A2 = <1; 1; 4>не пропорциональны, следовательно, А1 и А2 не коллинеарны, поэтому прямые либо пересекаются, либо скрещиваются.
Составьте уравнение плоскости A, проходящей через прямую L1 параллельно вектору А2. Если L1 и L2 пересекаются, то прямая L2 будет лежать в этой плоскости; если же L1 и L2 скрещиваются, то L2 параллельна плоскости A, и тогда расстояние между L1 и L2 (длина общего перпендикуляра) будет равно расстоянию от любой точки прямой L2 до плоскости A.
Координаты направляющих векторов данных прямых A1 = <3; 2; -2>и
A2 = <1; 1; 4>не пропорциональны, следовательно, А1 и А2 не коллинеарны, поэтому прямые либо пересекаются, либо скрещиваются.
Составим уравнение плоскости A, проходящей через прямую L1 параллельно вектору А2. Если L1 и L2 пересекаются, то прямая L2 будет лежать в этой плоскости (рис.9); если же L1 и L2 скрещиваются, то L2 параллельна плоскости A, и тогда расстояние между L1 и L2 (длина общего перпендикуляра) будет равно расстоянию от любой точки прямой L2 до плоскости A (рис.10).
[A1, A2] = (10; -14; 1) = N, точка А= <5; 0; -25>лежит на прямой L1, следова-тельно, она лежит и в плоскости A. Тогда уравнение плоскости A имеет вид:
Точка В= <1; 2; 13>принадлежит прямой L2. Проверим, лежит ли эта точка в плоскости A:
Тогда искомой величиной будет расстояние от В до A. Его можно найти, составив нормальное уравнение плоскости A:
Ответ: 
Найти точку, симметричную точке А(5; -10; 4) относительно плоскости
Искомая точка В лежит на прямой, проходящей через точку А перпендикулярно плоскости A так, что ОА = ОВ, где точка О – точка пересечения A с прямой АВ.
Искомая точка В лежит на прямой, проходящей через точку А перпендикулярно плоскости A так, что ОА = ОВ, где точка О – точка пересечения A с прямой АВ. Составим уравнения прямой АВ. Эта прямая перпендикулярна A, поэтому ее направляющим вектором можно считать нормаль к плоскости A: A = N = (1; -3; 1).
Параметрические уравнения прямой АВ имеют вид:
Точка О принадлежит и прямой АВ, и плоскости A, поэтому ее координаты должны удовлетворять и уравнениям прямой, и уравнению плоскости. Подставим в уравнение плоскости A параметрические выражения для X, Y, Z из уравнений прямой АВ:
T + 5 – 3(-3T – 10) + T + 4 – 6 = 0; 11T + 33 = 0; T = -3.
Итак, координаты точки О:
Поскольку точка О – середина отрезка АВ, то
http://ru.onlinemschool.com/math/assistance/cartesian_coordinate/plane/
http://matica.org.ua/metodichki-i-knigi-po-matematike/lineinaia-algebra-i-analiticheskaia-geometriia/4-2-10-primery-resheniia-zadach-po-teme-uravnenie-ploskosti-v-prostranstve