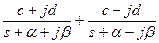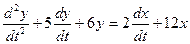Контрольная работа: Передаточные функции одноконтурной системы
| Название: Передаточные функции одноконтурной системы Раздел: Рефераты по математике Тип: контрольная работа Добавлен 21:52:15 24 декабря 2010 Похожие работы Просмотров: 508 Комментариев: 14 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать | ||||||||||||||||||||||||||||||||||||
| 1 | 3y (3) +6y (2) — 3y = u (2) — 2u (1) + u | 10 | 3y (3) +3y (2) + 2y (1) -y = — 4u (1) + u |
| 2 | y (3) — 3y (2) + 2y (1) + 5y = 3u (2) + u | 11 | 5y (3) — 5y = 3u (2) -2u (1) + u |
| 3 | -2y (3) + 4y (2) +2y (1) -5y = u (2) — 3u (1) + u | 12 | 4y (3) -3y (2) + 6y (1) + 2y = 3u (2) -2u (1) |
| 4 | 3y (3) — 4y (2) + 2y (1) =3u (2) — u (1) | 13 | 12y (3) + 4y (2) + 3y (1) + 2y = 3 u |
| 5 | 5y (3) — 7y (2) — 3y (1) = 2u (2) — u | 14 | 6y (3) — 4y (2) +-2y (1) = 6u (2) — 3u (1) + u |
| 6 | -3y (3) + 4y (2) + 6y (1) + 5y = -3 u | 15 | 8y (3) +3y (2) — 3y = -5u (2) — 3u (1) + u |
| 7 | 2y (3) — 4y (2) + 5y = — 3u (1) + u | 16 | 3y (3) + 3y (1) + 5y = 5u (2) +2u (1) + u |
| 8 | 6y (3) -+y (2) -y (1) = — 3u (1) + u | 17 | -4y (3) + 4y (2) -2y (1) + 7y = 5 u |
| 9 | — 4y (2) + 3y (1) + 5y = — 2u (1) + u | 18 | 3y (3) — 2y (2) — 3y (1) = u (2) — 4u (1) +2 u |
Задание 2
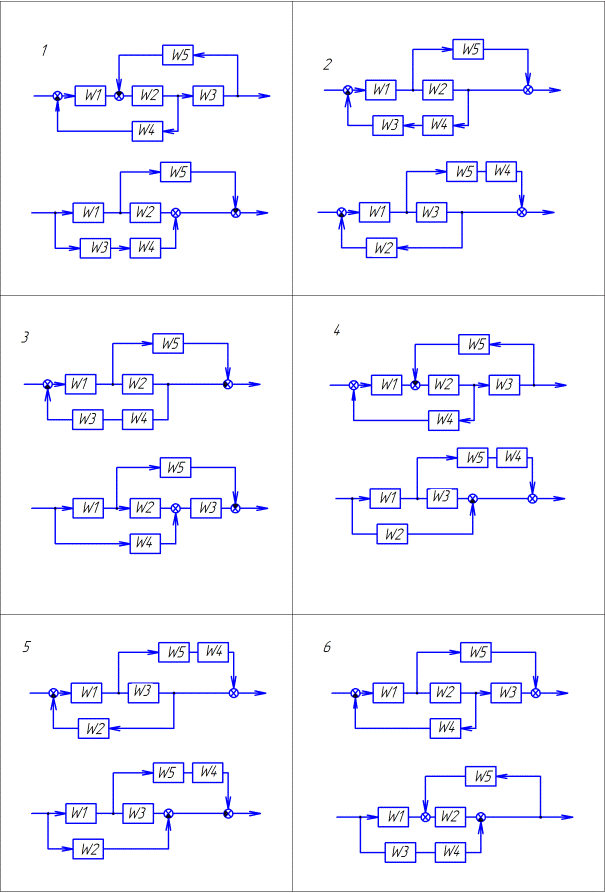
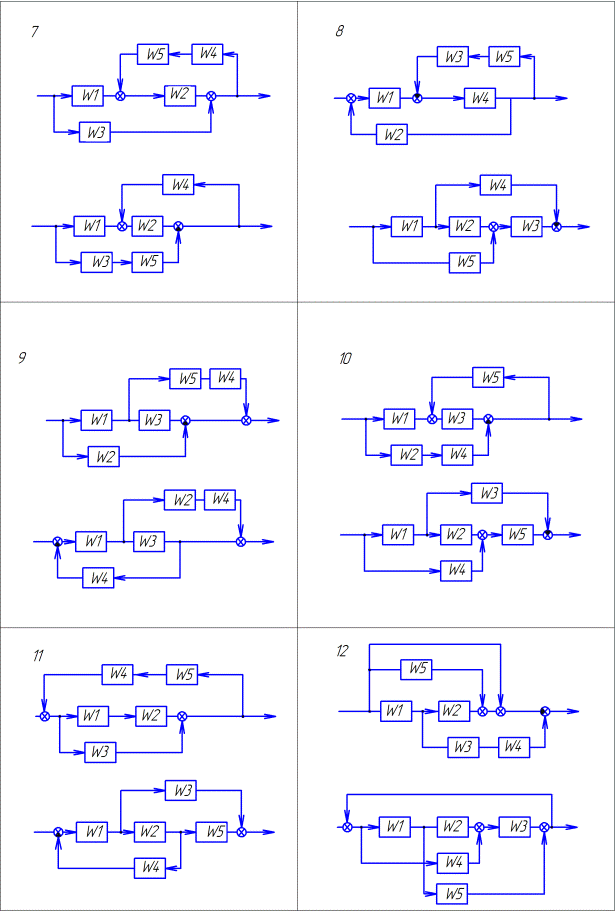
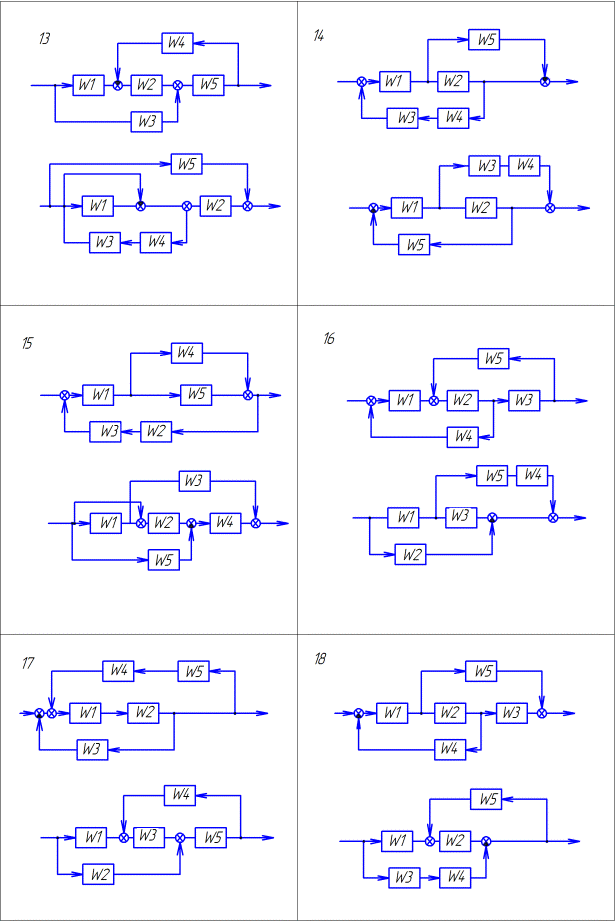
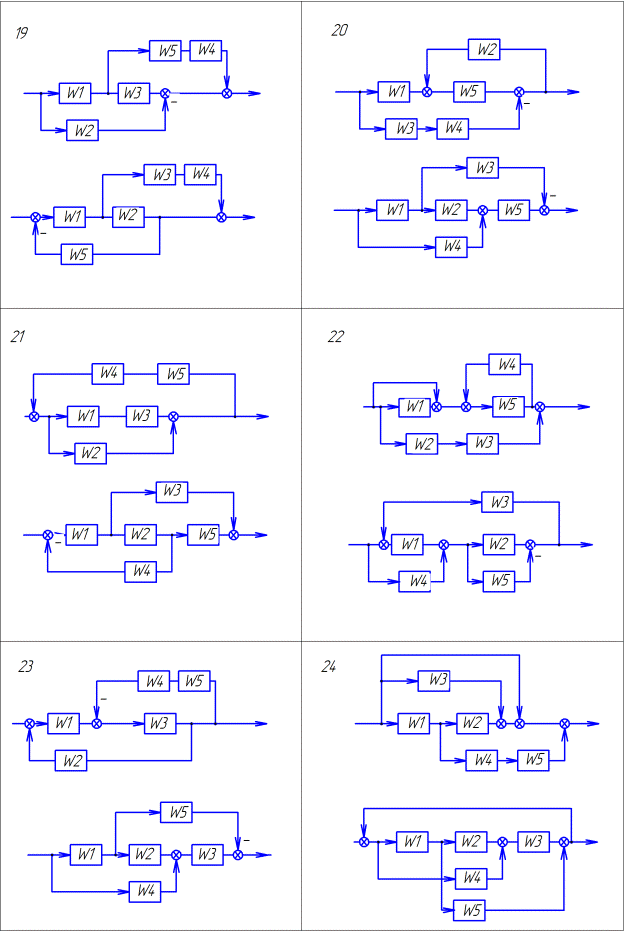
Преобразовать структурную схему и определить эквивалентную передаточную функцию. Варианты заданий приведены в таблице 1. (смотреть примеры 1-4)
Таблица 1.1. Варианты заданий по теме «Структурные схемы»
Продолжение таблицы 1.1. Варианты заданий
Продолжение таблицы 1.1. Варианты заданий
Продолжение таблицы 1.1. Варианты заданий
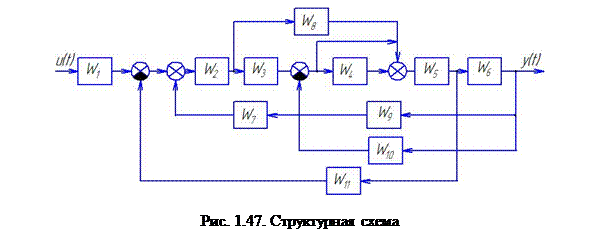
Задание 3. (без вариантов заданий, общее). Записать в общем виде главную передаточную функцию системы (рис. 1.47).
ПРЕОБРАЗОВАНИЯ ЛАПЛАСА – теоретическая часть
Общие сведения
В ТАУ основным инженерным методом решения дифференциальных уравнений, т. е. исследования поведения систем во времени, является преобразование Лапласа. Его преимущество заключается в том, что операции дифференцирования и интегрирования оно заменяет более простыми алгебраическими операциями умножения и деления.
Рассмотрим принцип решения дифференциальных уравнений с помощью преобразования Лапласа.
1. На первом этапе производят прямое преобразование X ( s ) = L – от функции времени переходят к функции комплексной переменной Лапласа s = σ + jω = α + jβ.
Здесь ω = 2π f – это известная из электротехники круговая частота, рад/с.
2. Далее решают алгебраическое уравнение реакции, для чего находят собственные значения системы, т. е. корни характеристического уравнения D ( s ) = 0, и по теореме разложения определяют коэффициенты числителей простых дробей, на которые в соответствии с собственными значениями разлагается реакция.
3. В конце вычислений выполняют обратное преобразование Лапласа x ( t ) = L -1 – от функции переменной s возвращаются к функции переменной t.
Общее обозначение описанных операций x ( t )÷ X ( s ), где слева строчными буквами изображена функция времени (оригинал), справа, прописной буквой – функция комплексного переменного (изображение), а между ними стоит символ соответствия (ни в коем случае не равенства, что будет являться грубой ошибкой!).
Таблица 2. Таблица соответствия оригиналов и изображений
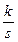
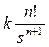
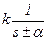
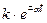 – экспонента
– экспонента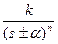
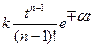 , при n > 1
, при n > 1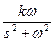
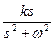
сопряженные комплексные корни
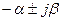
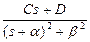
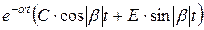 б) через синус
б) через синус 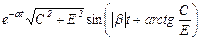 в) через косинус
в) через косинус 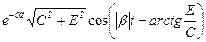
сопряженные комплексные корни
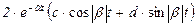 перед d ставят плюс, если знаки мнимых частей изображения в числителе и знаменателе совпадают (как показано), и минус в противном случае
перед d ставят плюс, если знаки мнимых частей изображения в числителе и знаменателе совпадают (как показано), и минус в противном случаеЗакон изменения выходного сигнала обычно является функцией, которую необходимо найти, а входной сигнал, как правило, известен.
Некоторые типовые входные и их изображения:
единичное ступенчатое воздействие имеет изображение X ( s ) = 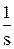
дельта-функция X ( s ) = 1,
линейное воздействие X(s) = 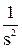
Пример. Решение ДУ с использованием преобразований Лапласа.
Допустим, входной сигнал имеет форму единичного ступенчатого воздействия, т.е. x(t) = 1. Тогда изображение входного сигнала, согласно таблице 2, имеет вид X(s) = 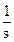
Производим преобразование исходного ДУ по Лапласу и подставляем X(s):
s 2 ×Y(s) + 5×s×Y(s) + 6×Y(s) = 2×s×X(s) + 12×X(s),
s 2 ×Y(s) + 5×s×Y(s) + 6×Y(s) = 2×s 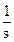
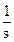
Y(s)×(s 3 + 5s 2 + 6s) = 2×s + 12.
Определяется выражение для Y:
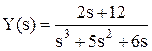
Оригинал полученной функции отсутствует в таблице оригиналов и изображений. Для решения задачи его поиска дробь разбивается на сумму простых дробей с учетом того, что знаменатель может быть представлен в виде s ( s + 2)( s + 3):
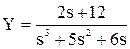
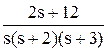
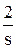
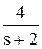
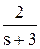
Теперь, используя табличные функции (см. табл. 2), определяется оригинал выходной функции:
y(t) = 2 — 4 . e -2 t + 2 . e -3 t .
При решении ДУ с использованием преобразований Лапласа часто встает промежуточная задача разбиения дроби на сумму простых дробей. Существуют два пути решения этой задачи:
— путем решения системы уравнений относительно коэффициентов числителей,
— путем расчета коэффициентов числителей по известным формулам.
Общий алгоритм разбиения дроби на сумму простых дробей:
шаг 1 – определяются корни знаменателя si (знаменатель дроби приравнивается к нулю и решается полученное уравнение относительно s);
шаг 2 – каждому корню ставится в соответствие простая дробь вида 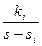
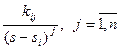
шаг 3 – определяются коэффициенты ki по одному из вариантов расчета.
Продолжение метода:
Даны дифференциальные уравнения состояния определить передаточную функцию объекта
Взаимосвязь видов математических моделей многомерных систем
Выше были рассмотрены два вида моделей многомерной системы. Установим связь между этими двумя видами. Так как исходной базой для математических моделей являются дифференциальные уравнения, то логичным будет определить связь уравнений состояния с передаточными матрицами САУ. Для этого применим преобразование Лапласа к уравнениям состояния и выхода
при нулевых начальных условиях, заменим оригиналы переменных изображениями по Лапласу и получим систему векторно-матричных операторных уравнений
Определим связь между вектором входа и векторами состояния и выхода. Из первого уравнения системы (3) имеем
и если матрица 

Откуда следует, что
Подставив (4) в (3), получаем

В результате получаем
Вспомним, что компонентами эквивалентных матриц являются передаточные функции системы. Следовательно, выражения (5) и (6) представляют собой универсальные формулы для вычисления всех необходимых для анализа передаточных функций многомерной системы, по которым могут быть получены структурные схемы и частотные характеристики.
Заметим, что каждый элемент эквивалентных матриц (передаточных функций) имеет, по определению обратной матрицы, сомножитель
То есть полином 
является характеристическим уравнением системы.
Таким образом, мы не только получили связь между математическими моделями во временной и частотной областях, но и универсальные выражения для определения передаточных функций и характеристических уравнений любых линейных объектов или систем управления. Исходными параметрами для выражений (5),(6) и (7) являются матрицы параметров уравнений состояния и выхода. Выполнить преобразования (5),(6) и (7) можно с помощью компьютера, имеющего программы символьной математики, на пример, такие, как Mathematica 3.0 (4.0), разработанные Wolfram Research. в системах второго и третьего порядка эти преобразования можно производить и вручную.
Рассмотрим несколько примеров получения и преобразования моделей.
Рассмотрим объект, принципиальная электрическая схема которого показана на рис. 1.
Выполним для этого объекта следующие задачи:
Получить уравнение состояния.
Определить характеристическое уравнение объекта.
Определить передаточную матрицу объекта.
Получение уравнения состояния
Запишем дифференциальные уравнения, описывающие процессы в схеме
Зададим векторы состояния и входа:
Получаем, что 
Раскроем в (9) матричные скобки:
Приведем систему уравнений (8) к виду (10), используя при отсутствии переменной в правых частях нулевые коэффициенты:
Теперь известны все компоненты матриц параметров, и можно записать уравнение состояния

Следовательно, матрицы параметров имеют следующий вид
Определение характеристического уравнения объекта
Характеристическое уравнение системы определим по матрицам параметров уравнения состояния (11), используя выражение (7)
Подставив в (12) выражения для матрицы параметров 

Определение передаточной матрицы объекта
Определим эквивалентную матрицу передаточных функций, которая связывает векторы состояния и управления по выражению (5), которое для нашего случая имеет вид:
Матрица 

Определим обратную матрицу, помня о том, 

где 



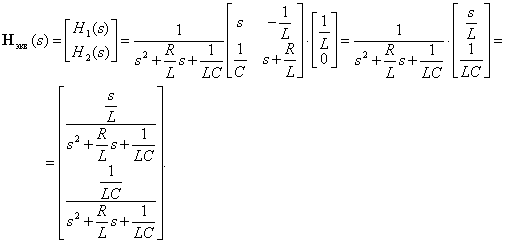
Следовательно, получаем передаточные функции объекта

Электродвигатель постоянного тока независимого возбуждения (с постоянными магнитами) как объект управления описывается следующей системой дифференциальных уравнений
где 


Получение уравнения состояния
Зададим векторы состояния и входа:
Получаем, что 
Раскроем в (16) матричные скобки:
Приведем систему уравнений (15) к виду (17), используя при отсутствии переменной в правых частях нулевые коэффициенты:
Теперь известны все компоненты матриц параметров, и можно записать уравнение состояния в развернутой форме

Следовательно, матрицы параметров имеют следующий вид
Определение характеристического уравнения объекта
Характеристическое уравнение системы определим по матрицам параметров уравнения состояния (18), используя выражение (7)
Подставив в (19) выражения для матрицы параметров 

Определение передаточной матрицы объекта
Определим эквивалентную матрицу передаточных функций, которая связывает векторы состояния и управления по выражению (5), которое для нашего случая имеет вид:
Матрица 

Определим обратную матрицу

Следовательно, получаем передаточные функции объекта
Контрольные вопросы и задачи
Поясните, как связаны между собой модели во временной и частотной области?
Как определить по уравнению состояния характеристическое уравнение?
Как определить по уравнению состояния матрицу передааточных функций системы?
По уравнению состояния

описывающему многомерную систему, определить характеристическое уравнение системы.

По уравнению состояния

описывающему многомерную систему, определить характеристическое уравнение системы.

По уравнению состояния

описывающему многомерную систему, определить матрицу передаточных функций системы.

http://megaobuchalka.ru/17/40072.html
http://drive.ispu.ru/elib/lebedev/15.html
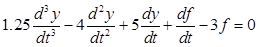 ; б)
; б)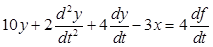 .
.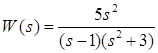 .
.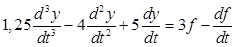 .
. .
. , то получается уравнение Y(s) = WF(s).F(s). Структурная схема объекта приведена на рис. 1.
, то получается уравнение Y(s) = WF(s).F(s). Структурная схема объекта приведена на рис. 1.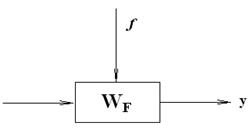
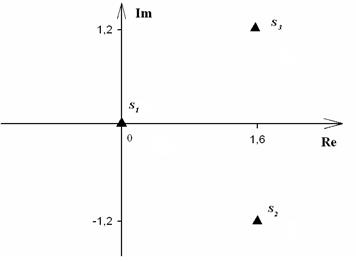
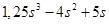 .
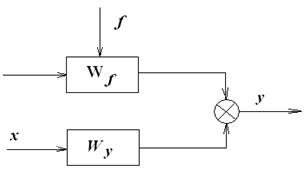
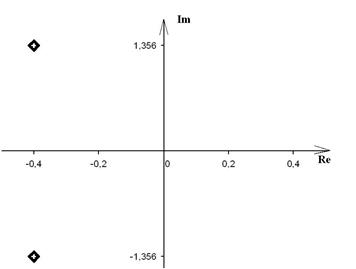
.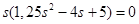 , корни которого:
, корни которого: ,
, 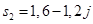 и
и 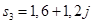 .
.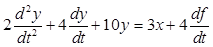 .
.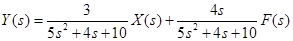 .
.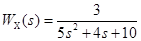 и
и  ,
,
 ,
, .
.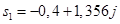 и
и 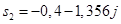 .
.
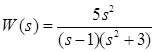
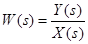 , получим:
, получим: , тогда:
, тогда: .
.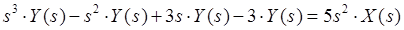
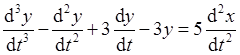 .
.
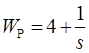 ;
;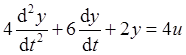 .
.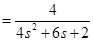 .
.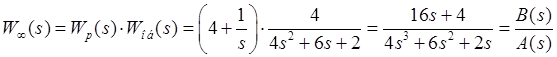
 ;
;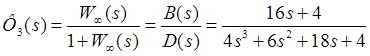 — по заданию;
— по заданию;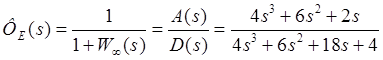 — по ошибке;
— по ошибке;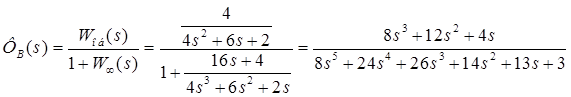 — по возмущению.
— по возмущению.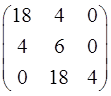
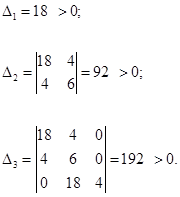
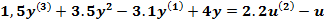
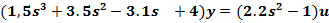
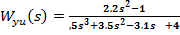 .
.