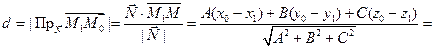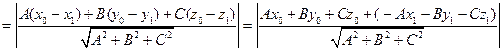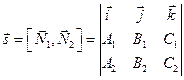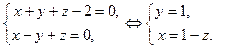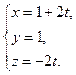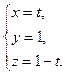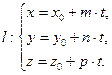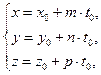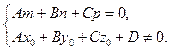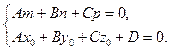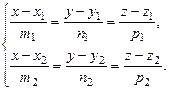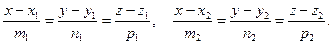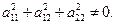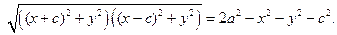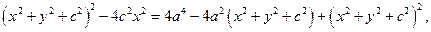Даны две плоскости заданные своими уравнениями

Уравнения прямой в пространстве — это уравнения двух пересекающихся плоскостей

В данном разделе продолжим изучение темы уравнения прямой в пространстве с позиции стереометрии. Это значит, что мы будем рассматривать прямую линию в трехмерном пространстве как линию пересечения двух плоскостей.

Согласно аксиомам стереометрии, если две плоскости не совпадают и имеют одну общую точку, то они также имею одну общую прямую, на которой лежат все точки, которые являются общими для двух плоскостей. Используя уравнения двух пересекающихся плоскостей, мы можем определить прямую линию в прямоугольной системе координат.

По ходу рассмотрения темы приведем многочисленные примеры, ряд графических иллюстраций и развернутых решений, необходимых для лучшего усвоения материала.

Уравнения двух плоскостей, задающих прямую линию в пространстве

Пусть даны две плоскости, которые не совпадают между собой и пересекаются. Обозначим их как плоскость α и плоскость β . Разместим их в прямоугольной системе координат O х у z трехмерного пространства.

Как мы помним, любую плоскость в прямоугольной системе координат задает общее уравнение плоскости вида A x + B y + C z + D = 0 . Будем считать, что плоскости α соотвествует уравнение A 1 x + B 1 y + C 1 z + D 1 = 0 , а плоскости β уравнение A 2 x + B 2 y + C 2 z + D 2 = 0 . В этом случае нормальные вектора плоскостей α и β n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) не коллинеарны, так как плоскости не совпадают между собой и е размещаются параллельно друг другу. Запишем это условие следующим образом:

n 1 → ≠ λ · n 2 → ⇔ A 1 , B 1 , C 1 ≠ λ · A 2 , λ · B 2 , λ · C 2 , λ ∈ R

Чтобы освежить в памяти материал по теме «Параллельность плоскостей», смотрите соответствующий раздел нашего сайта.

Линию пересечения плоскостей обозначим буквой a . Т.е. a = α ∩ β . Эта прямая представляет собой множество точек, которые являются общими для обеих плоскостей α и β . Это значит, что все точки прямой линии a удовлетворяют обоим уравнениям плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . Фактически, они являются частным решением системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .

Общее решение системы линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 определяет координаты всех точек линии, по которой происходит пересечение двух плоскостей α и β . Это значит, что с его помощью мы можем определить положение прямой в прямоугольной системе координат O x y z .

Рассмотрим описанную теорию еще раз, теперь уже на конкретном примере.

Прямая O x – это прямая, по которой пересекаются координатные плоскости O x y и O x z . Зададим плоскость O x y уравнением z = 0 , а плоскость O x z уравнением у = 0 . Такой подход мы подробно разобрали в разделе «Неполное общее уравнение плоскости», так что, в случае затруднений, можно обратиться к этому материалу повторно. В этом случае координатная прямая O x определяется в трехмерной системе координат системой из двух уравнений вида y = 0 z = 0 .

Нахождение координат точки, лежащей на прямой, по которой пересекаются плоскости

Рассмотрим задачу. Пусть в трехмерном пространстве задана прямоугольная система координат O х у z . Линия, по которой пересекаются две плоскости a , задана системой уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 . Дана точка трехмерного пространства M 0 x 0 , y 0 , z 0 .

Давайте определим, принадлежит ли точка M 0 x 0 , y 0 , z 0 заданной прямой линии a .

Для того, чтобы получить ответ на вопрос задачи, подставим координаты точки М 0 в каждое из двух уравнений плоскости. Если в результате подстановки оба уравнения превратятся в верные равенства A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 , то точка М 0 принадлежит каждой из плоскостей и принадлежит заданной линии. Если хотя бы одно из равенств A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 окажется неверным, то точка М 0 не принадлежит прямой линии.

Рассмотрим решение примера

Прямая линия задана в пространстве уравнениями двух пересекающихся плоскостей вида 2 x + 3 y + 1 = 0 x — 2 y + z — 3 = 0 . Определите, принадлежат ли точки M 0 ( 1 , — 1 , 0 ) и N 0 ( 0 , — 1 3 , 1 ) прямой линии пересечения плоскостей.

Решение

Начнем с точки М 0 _. Подставим ее координаты в оба уравнения системы 2 · 1 + 3 · ( — 1 ) + 1 = 0 1 — 2 · ( — 1 ) + 0 — 3 = 0 ⇔ 0 = 0 0 = 0 .

В результате подстановки мы получили верные равенства. Это значит, что точка М 0 принадлежит обеим плоскостям и расположена на линии их пересечения.

Подставим в оба уравнения плоскости координаты точки N 0 ( 0 , — 1 3 , 1 ) . Получаем 2 · 0 + 3 · — 1 3 + 1 = 0 0 — 2 · — 1 3 + 1 — 3 = 0 ⇔ 0 = 0 — 1 1 3 = 0 .

Как вы видите, второе уравнение системы превратилось в неверное равенство. Это значит, что точка N 0 не принадлежит заданной прямой.

Ответ: точка М 0 принадлежит прямой линии, а точка N 0 не принадлежит.

Теперь предлагаем вам алгоритм нахождения координат некоторой точки, принадлежащей прямой линии, если прямая в пространстве в прямоугольной системе координат O x y z определяется уравнениями пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .

Количество решений системы из двух линейных уравнений с темя неизвестными A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 бесконечно. Любое из этих решений может стать решением задачи.

Пусть в трехмерном пространстве задана прямая линия уравнениями двух пересекающихся плоскостей вида x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 . Найдите координаты любой из точек этой прямой.

Решение

Перепишем систему уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 ⇔ x + 0 y + 3 z = — 7 2 x + 3 y + 3 z = — 2 .

Возьмем отличный от нуля минор второго порядка в качестве базисного минора основной матрицы системы 1 0 2 3 = 3 ≠ 0 . Это значит, что z – это свободная неизвестная переменная.

Перенесем слагаемые, содержащие свободную неизвестную переменную z в правые части уравнений:

x + 0 y + 3 z = — 7 2 x + 3 y + 3 z = — 2 ⇔ x + 0 y = — 7 — 3 z 2 x + 3 y = — 2 — 3 z

Введем произвольное действительное число λ и примем, что z = λ .

Тогда x + 0 y = — 7 — 3 z 2 x + 3 y = — 2 — 3 z ⇔ x + 0 y = — 7 — 3 λ 2 x + 3 y = — 2 — 3 λ .

Для решения полученной системы уравнений применим метод Крамера:

∆ = 1 0 2 3 = 1 · 3 — 0 · 1 = 2 ∆ x = — 7 — 3 λ 0 — — 3 λ 3 = — 7 — 3 λ · 3 — 0 · ( — 2 — 3 λ ) = 21 — 9 λ ⇒ x = ∆ x ∆ = — 7 — 3 λ ∆ y = 1 — 7 — 3 λ 2 — 2 — 3 λ = 1 · — 2 — 3 λ — — 7 — 3 λ · = 12 + 3 λ ⇒ y = ∆ y ∆ = 4 + λ

Общее решение системы уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 будет иметь вид x = — 7 — 3 λ y = 4 + λ z = λ , где λ ∈ R .

Для получения частного решения системы уравнений, которое даст нам искомые координаты точки, принадлежащей заданной прямой, нам необходимо взять конкретное значение параметра λ . Если λ = 0 , то x = — 7 — 3 · 0 y = 4 + 0 z = 0 ⇔ x = — 7 y = 4 z = 0 .

Это позволяет нам получить координаты искомой точки — 7 , 4 , 0 .

Проверим верность найденных координат точки методом подстановки их в исходные уравнения двух пересекающихся плоскостей — 7 + 3 · 0 + 7 = 0 2 · ( — 7 ) + 3 · 4 + 3 · 0 + 2 = 0 ⇔ 0 = 0 0 = 0 .

Ответ: — 7 , 4 , 0

Направляющий вектор прямой, по которой пересекаются две плоскости

Давайте рассмотрим, как определить координаты направляющего вектора прямой, которая задана уравнениями двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . В прямоугольной системе координат 0хуz направляющий вектор прямой неотделим от прямой линии.

Как мы знаем, прямая перпендикулярна по отношению к плоскости в том случае, когда она перпендикулярна по отношению к любой прямой, лежащей в данной плоскости. Исходя из вышесказанного, нормальный вектор плоскости перпендикулярен любому ненулевому вектору, лежащему в данной плоскости. Эти два факта помогут нам в нахождении направляющего вектора прямой.

Плоскости α и β пересекаются по линии a . Направляющий вектор a → прямой линии a расположен перпендикулярно по отношению к нормальному вектору n 1 → = ( A 1 , B 1 , C 1 ) плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и нормальному вектору n 2 → = ( A 2 , B 2 , C 2 ) плоскости A 2 x + B 2 y + C 2 z + D 2 = 0 .

Направляющий вектор прямой a представляет собой векторное произведение векторов n → 1 = ( A 1 , B 1 , C 1 ) и n 2 → = A 2 , B 2 , C 2 .

a → = n → 1 × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2

Зададим множество всех направляющих векторов прямой как λ · a → = λ · n 1 → × n 2 → , где λ — это параметр, который может принимать любые действительные значения, отличные от нуля.

Пусть прямая в пространстве в прямоугольной системе координат O х у z задана уравнениями двух пересекающихся плоскостей x + 2 y — 3 z — 2 = 0 x — z + 4 = 0 . Найдем координаты любого направляющего вектора этой прямой.

Решение

Плоскости x + 2 y — 3 z — 2 = 0 и x — z + 4 = 0 имеют нормальные векторы n 1 → = 1 , 2 , — 3 и n 2 → = 1 , 0 , — 1 . Примем за направляющий вектор прямой линии, являющейся пересечением двух заданных плоскостей, векторное произведение нормальных векторов:

a → = n → 1 × n 2 → = i → j → k → 1 2 — 3 1 0 — 1 = i → · 2 · ( — 1 ) + j → · ( — 3 ) · 1 + k → · 1 · 0 — — k → · 2 · 1 — j → · 1 · ( — 1 ) — i → · ( — 3 ) · 0 = — 2 · i → — 2 j → — 2 k →

Запишем ответ в координатной форме a → = — 2 , — 2 , — 2 . Тем, кто не помнит, как это делается, рекомендуем обратиться к теме «Координаты вектора в прямоугольной системе координат».

Ответ: a → = — 2 , — 2 , — 2

Переход к параметрическим и каноническим уравнениям прямой в пространстве

Для решения ряда задач проще использовать параметрические уравнения прямой в пространстве вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ или канонические уравнения прямой в пространстве вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ . В этих уравнениях a x , a y , a z — координаты направляющего вектора прямой, x 1 , y 1 , z 1 — координаты некоторой точки прямой, а λ — параметр, принимающий произвольные действительные значения.

От уравнения прямой вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 можно перейти к каноническим и параметрическим уравнениям прямой линии в пространстве. Для записи канонических и параметрических уравнений прямой нам понадобятся навыки нахождения координат некоторой точки прямой, а также координат некоторого направляющего вектора прямой, заданной уравнениями двух пересекающихся плоскостей.

Рассмотрим написанное выше на примере.

Зададим прямую линию в трехмерной системе координат уравнениями двух пересекающихся плоскостей 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 . Напишем канонические и параметрические уравнения этой прямой.

Решение

Найдем координаты направляющего вектора прямой, который является векторным произведением нормальных векторов n 1 → = 2 , 1 , — 1 плоскости 2 x + y — z — 1 = 0 и n 2 → = ( 1 , 3 , — 2 ) плоскости x + 3 y — 2 z = 0 :

a → = n 1 → × n 2 → = i → j → k → 2 1 — 1 1 3 — 2 = i → · 1 · ( — 2 ) + j → · ( — 1 ) · 1 + k → · 2 · 3 — — k → · 1 · 1 — j → · 2 · ( — 2 ) — i → · ( — 1 ) · 3 = i → + 3 · j → + 5 · k →

Координаты направляющего вектора прямой a → = ( 1 , 2 , 5 ) .

Следующим шагом является определение координат некоторой точки заданной прямой линии, которыми является одно из решений системы уравнений: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ 2 x + y — z = 1 x + 3 y — 2 z = 0 .

Возьмем в качестве минорной матрицы системы определитель 2 1 1 3 = 2 · 3 — 1 · 1 = 5 , который отличен от нуля. В этом случае переменная z является свободной. Перенесем слагаемые с ней в правые части каждого уравнения и придаем переменной произвольное значение λ :

2 x + y — z = 1 x + 3 y — 2 z = 0 ⇔ 2 x + y = 1 + z x + 3 y = 2 z ⇔ 2 x + y = 1 + λ x + 3 y = 2 λ , λ ∈ R

Применяем для решения полученной системы уравнений метод Крамера:

∆ = 2 1 1 3 = 2 · 3 — 1 · 1 = 5 ∆ x = 1 + λ 1 2 λ 3 = ( 1 + λ ) · 3 — 1 · 2 λ = 3 + λ ⇒ x = ∆ x ∆ = 3 + λ 5 = 3 5 + 1 5 · λ ∆ y = 2 1 + λ 1 2 λ = 2 · 2 λ — ( 1 + λ ) · 1 = — 1 + 3 λ ⇒ y = ∆ y ∆ = — 1 + 3 λ 5 = — 1 5 + 3 5 · λ

Получаем: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ x = 3 5 + 1 5 y = — 1 5 + 3 5 z = λ

Примем λ = 2 для того, чтобы получить координаты точки прямой линии: x 1 = 3 5 + 1 5 · 2 y 1 = — 1 5 + 3 5 · 2 z 1 = 2 ⇔ x 1 = 1 y 1 = 1 z 1 = 2 . Теперь мы имеем достаточно данных для того, чтобы записать канонические и параметрические уравнения данной прямой в пространстве: x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ x — 1 1 = y — 1 3 = z — 2 5 x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ x = 1 + 1 · λ y = 1 + 3 · λ z = 2 + 5 · λ ⇔ x = 1 + λ y = 1 + 3 · λ z = 2 + 5 · λ

Ответ: x — 1 1 = y — 1 3 = z — 2 5 и x = 1 + λ y = 1 + 3 · λ z = 2 + 5 · λ

Данная задача имеет еще один способ решения.

Нахождение координат некоторой точки прямой проводится при решении системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .

В общем случае ее решения можно записать в виде искомых параметрических уравнений прямой в пространстве x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ .

Получение канонических уравнений проводится следующим образом: решаем каждое из полученных уравнений относительно параметра λ , приравниваем правые части равенства.

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y λ = z — z 1 a z ⇔ x — x 1 a x = y — y 1 a y = z — z 1 a z

Применим данный способ к решению задачи.

Зададим положение прямой линии уравнениями двух пересекающихся плоскостей 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 . Напишем параметрическое и каноническое уравнения для этой прямой линии.

Решение

Решение системы из двух уравнений с тремя неизвестными проводится аналогично тому, как мы делали это в предыдущем примере. Получаем: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ x = 3 5 + 1 5 · λ y = — 1 5 + 3 5 · λ z = λ .

Это параметрические уравнения прямой в пространстве.

Канонические уравнения получаем следующим образом: x = 3 5 + 1 5 · λ y = — 1 5 + 3 5 · λ z = λ ⇔ λ = x — 3 5 1 5 λ = y + 1 5 3 5 λ = z 1 ⇔ x — 3 5 1 5 = y + 1 5 3 5 = z 1

Полученные в обоих примерах уравнения отличаются внешне, однако они эквивалентны, так как определяют одно и то же множество точек трехмерного пространства, а следовательно и одну и ту же прямую линию.

Ответ: x — 3 5 1 5 = y + 1 5 3 5 = z 1 и x = 3 5 + 1 5 · λ y = — 1 5 + 3 5 · λ z = λ

Аналитическая геометрия на плоскости и в пространстве. 2 страница

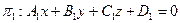
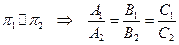
1. Если плоскости параллельны и , то их нормальные векторы коллинеарны, то есть их координаты пропорциональны:

.

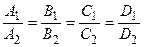
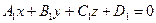
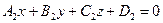
Если же выполняются равенства , то уравнения и определяют одну и ту же плоскость.

2. Если плоскости перпендикулярны, то их нормальные векторы ортогональны, то есть их скалярное произведение равно нулю

.

2.4.3 Расстояние от точки до плоскости.

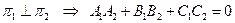
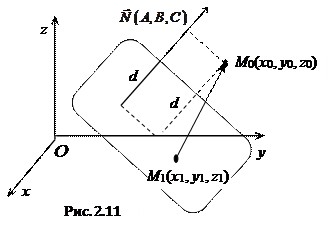
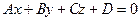
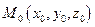
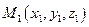
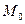
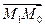
Пусть плоскость π задана уравнением , – произвольная точка пространства. Для любой точки , лежащей на плоскости, расстояние d от точки до плоскости π равно абсолютной величине проекции вектора на нормальный вектор .

Вектор , следовательно

Так как из принадлежности точки плоскости π следует, что , т.е. , то

. (2.9)

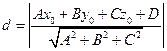
2.4.4. Уравнение плоскости, проходящей через три заданные точки.

Пусть даны три точки , и , не лежащие на одной прямой (т.е. векторы и не коллинеарны). Введем в задачу точку – текущую точку плоскости. Векторы , и лежат в одной плоскости, т.е. компланарны, следовательно, их смешанное произведение равно нулю: , или, в координатной форме,

. (2.10)

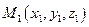
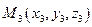
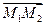
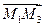
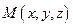
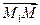
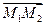
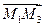
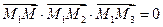
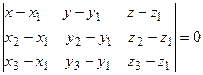
Уравнение вида (2.10) называется уравнением плоскости, проходящей через три данные точки.

2.4.5. Уравнение плоскости в отрезках.

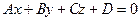
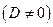
Рассмотрим плоскость, не проходящую через начало координат и заданную своим общим уравнением . Представим данное уравнение в виде

.

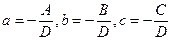
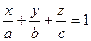
Обозначая , получим уравнение

, (2.11)

которое называется уравнением плоскости в отрезках.К виду в отрезках может быть приведено уравнение всякой плоскости, не проходящей через начало координат.

Отметим, что точки с координатами (a;0;0), (0;b;0) и (0;0;c) являются точками

пересечения плоскости с осями координат.

§2.5.Прямая в пространстве.

2.5.1. Общие уравнения прямой.

В пространстве прямая определяется пересечением двух плоскостей: .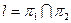

2.5.1.1. Определение. Система уравнений

(2.12)

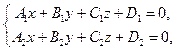
называется общими уравнениями прямой в пространстве.

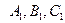
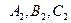
Система уравнений вида (2.12) задает прямую в пространстве тогда и только тогда, когда коэффициенты не пропорциональны коэффициентам .

Доказательство очевидно, так как пропорциональность коэффициентов эквивалентна параллельности плоскостей.

2.5.1.3. Определение. Пучком плоскостей называется совокупность всех плоскостей, проходящих через одну и ту же прямую.

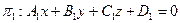
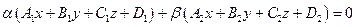
Если прямая определяется уравнениями двух плоскостей, принадлежащих пучку плоскостей, и , то уравнение пучка плоскостей можно представить в виде линейной комбинации данных уравнений, то есть . Полученное уравнение называется уравнением пучка плоскостей.

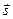
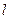
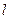
2.5.2. Определение. Ненулевой вектор , параллельный прямой , называется направляющим вектором прямой .

2.5.3. Векторное, параметрические и канонические уравнения прямой.

Пусть в пространстве задан ненулевой вектор и точка . Проведем прямую через точку в направлении вектора . Очевидно, произвольная точка принадлежит прямой при условии, что вектор коллинеарен вектору .

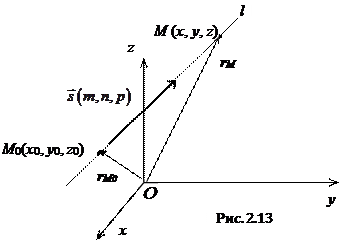
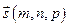
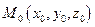
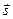
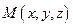
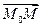
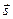
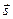
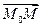
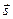
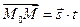
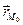
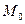
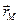
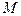
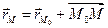
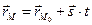
Так как вектор является ненулевым, условие коллинеарности векторов и имеет вид . Если – радиус-вектор точки , – радиус-вектор точки , то для любой точки М прямой выполняется , или

. (2.13)

Это уравнение называется векторным уравнением прямой в пространстве.

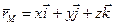
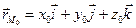
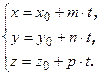
Запишем векторное уравнение (2.13) в координатной форме. Так как , , получим

(2.14)

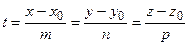
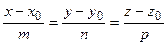
Эти уравнения называется параметрическими уравнением прямой в пространстве.Исключим из этих уравнений параметр t: . Уравнения

(2.15)

называется каноническими уравнениями прямой в пространстве.

2.5.4. Связь общих уравнений прямой с параметрическими.

Для того, чтобы записать параметрические уравнения прямой, заданной своими общими уравнениями

1. Найти направляющий вектор прямой;

2. Найти точку, принадлежащую прямой.

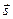
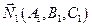
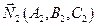
Направляющий вектор находится как векторное произведение векторов нормали плоскостей, задающих прямую вектором и :

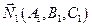
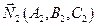
Для того, чтобы найти координаты какой-либо точки, принадлежащей прямой, требуется решить систему из двух уравнений с тремя неизвестными. Так как векторы и неколлинеарны (их координаты непропорциональны), то эта система имеет решение.

Пусть прямая задана своими общими уравнениями:

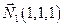
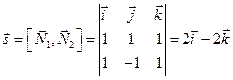
Найдем координаты нормальных векторов пересекающихся плоскостей, задающих прямую и . Следовательно, направляющий вектор прямой

.

Итак, 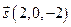. Найдем теперь какое-либо решение исходной системы уравнений. Складываем и вычитаем уравнения, получим:

Полагая , получим одну из точек, принадлежащих прямой .

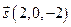
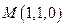
Таким образом, имеем направляющий вектор и точку , следовательно, параметрические уравнения прямой имеют вид

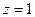
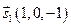
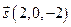
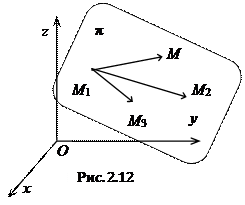
Заметим, что уравнение одной и той же прямой можно записать разными способами. Это определяется произвольностью выбора точки, принадлежащей прямой, а также произвольностью выбора направляющего вектора. Так, например, в предыдущем примере мы могли положить и получить точку , а в качестве направляющего взять вектор , коллинеарный с найденным вектором . Тогда параметрические уравнения той же прямой, очевидно, принимают вид

2.5.5. Уравнение прямой, проходящей через две заданные точки.

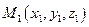
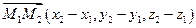
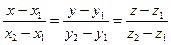
Пусть заданы две точки , и требуется найти уравнение прямой, проходящей через эти две точки. Очевидно, можно взять вектор в качестве направляющего вектора прямой, а в качестве точки, принадлежащей прямой, можно взять любую из точек М₁ или М₂. Следовательно, канонические уравнения прямой имеют вид:

(2.16)

2.5.6. Угол между прямыми.

Рассмотрим две прямые, заданные своими каноническими уравнениями

и .

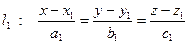
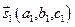
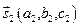
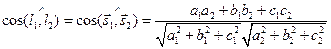
Очевидно, угол между прямыми будет равен углу между их направляющими векторами и :

. (2.17)

если прямые параллельны, то координаты их направляющих векторов пропорциональны

;

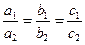
если прямые перпендикулярны, то их направляющие векторы ортогональны

.

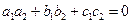
§2.6.Взаимное расположение прямых и плоскостей в пространстве.

2.6.1. Взаимное расположение прямой, заданной общими уравнениями, и плоскости.

В пространстве прямая может

а) пересекать плоскость;

б) быть параллельной плоскости;

в) лежать в плоскости.

Пусть плоскость задана общим уравнением

,

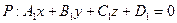
а прямая 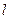задана общими уравнениями

Тогда взаимное расположение прямой и плоскостью определяется системой трех линейных уравнений относительно трех неизвестных:

(2.18)

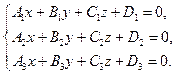
Если система уравнений (2.18) имеет единственное решение, то прямая и плоскость пересекаются; если у системы нет решений, то прямая параллельная плоскости; и, наконец, если у системы бесконечное множество решений, то прямая лежит в плоскости.

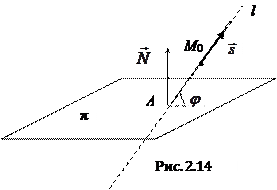
2.6.2. Взаимное расположение прямой, заданной параметрическими уравнениями, и плоскости.

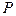
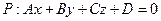
Пусть плоскость задана общим уравнением

,

а прямая 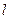задана параметрическими уравнениями

Подставим параметрические уравнения в уравнение плоскости. Получим линейное уравнение относительно параметра t

. (2.19)

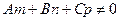
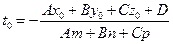
Если выполняется условие , то уравнение (2.19) разрешимо относительно параметра t

, (2.20)

и координаты точки пересечения прямой и плоскости имеют вид

где 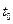определяется из (2.20).

Если , при этом , то уравнение (2.19) не разрешимо относительно параметра t, то есть прямая не пересекает плоскость. Таким образом, условие параллельности прямой и плоскости имеет вид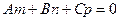

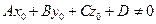
Если же оба коэффициента уравнения (2.19) равны нулю, то оно справедливо для любого значения параметра, то есть имеет бесконечное множество решений. Следовательно, прямая лежит в плоскости при условии

2.6.3. Угол между прямой и плоскостью.

Угол между прямой и плоскостью (т.е. угол между прямой и ее проекцией на плоскость) связан с углом между прямой и нормалью к плоскости соотношением , поэтому

.

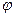
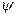
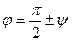
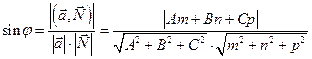
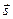
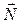
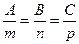
В частности, если векторы и коллинеарны, то есть

,

то прямая перпендикулярна плоскости.

2.6.4. Взаимное расположение двух прямых.

Две прямые в пространстве могут

а) быть компланарными, в том числе пересекаться, быть параллельными или совпадать;

б) не быть компланарными, то есть скрещиваться.

Пусть две прямые заданы своими каноническими уравнениями

, .

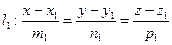
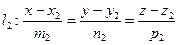
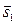
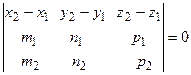
Прямые компланарны тогда, и только тогда, когда компланарны векторы , и . Таким образом, условие компланарности прямых l₁ и l₂ имеет вид

. (2.21)

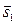
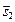
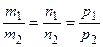
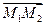
Если при этом векторы , коллинеарны, т.е. , то прямые параллельны. Если, дополнительно, вектор коллинеарен направляющим векторам, то прямые совпадают.

Если условие компланарности выполняется, но направляющие векторы неколлинеарны, то прямые пересекаются. Чтобы найти точку пересечения, надо решить систему уравнений

В этой системе три неизвестных (координаты точки пересечения х, у, z) и четыре уравнения, однако, если выполняются условия компланарности прямых и неколлинеарности направляющих векторов, она имеет единственное решение.

2.6.5. Расстояние от точки до прямой в пространстве.

Найдем расстояние от некоторой точки до прямой l, имеющей направляющий вектор и проходящей через точку . Очевидно, искомое расстояние будет являться высотой параллелограмма, построенного на векторах и . Используя геометрический смысл векторного произведения, окончательно получаем:

. (2.22)

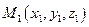
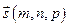
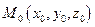
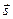
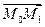
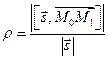
Чтобы найти расстояние между параллельными прямыми, нужно найти расстояние от произвольной точки первой прямой до второй прямой.

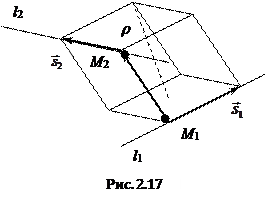
2.6.6. Расстояние между скрещивающимися прямыми.

Найдем расстояние между скрещивающимися прямыми, заданными своими каноническими уравнениями

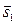
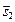
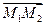
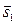
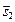
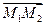
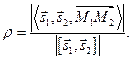
Так как прямые l₁ и l₂ скрещиваются, то векторы , и некомпланарны. Очевидно, что если построить параллелепипед на векторах , и (Рис. 2.17), то искомое расстояние r будет равно высоте параллелепипеда. С учетом свойств смешанного и векторного произведений получим

(2.23)

§2.7.Кривые второго порядка на плоскости.

2.7.1. Определение. Кривой второго порядка на плоскости называется множество точек плоскости, которое описывается уравнением второго порядка, то есть

(2.24)

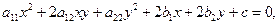
где

2.7.2. Определение. Канонической системой координатдля данной кривой называется декартова система координат, в которой уравнение кривой имеет наиболее простой вид.

2.7.3. Определение. Уравнение кривой в канонической системе координат называется ее каноническим уравнением.

2.7.4.1. Определение. Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух данных точек, называемых фокусами, является постоянной величиной.

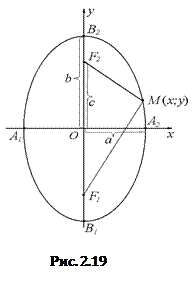
2.7.4.2. Каноническое уравнение эллипса.

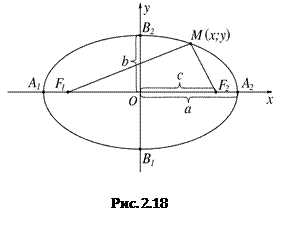
Введем на плоскости прямоугольную систему координат. Направим ось Ох вдоль линии, соединяющей фокусы F₁ и F₂, с серединой отрезка F₁F₂, а ось Оу – перпендикулярно через середину отрезка F₁F₂.

Пусть расстояние между фокусами равно 2с, а сумма расстояний от фокусов до произвольной точки равна 2а (a > c).

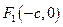
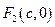
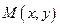
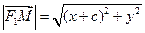
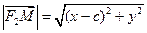
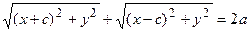
Тогда фокусы имеют координаты и , и, если – текущая точка эллипса, то расстояния от этой точки до фокусов равны длинам фокальных радиусов F₁M и F₂M: и . Тогда из определения эллипса

.

Возведем обе части уравнения в квадрат:

После преобразований получим:

Возводя обе части уравнения в квадрат, имеем:

.

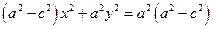
Обозначая , перепишем последнее уравнение в виде

, и после деления на правую часть окончательно получим

. (2.25)

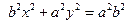
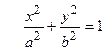
Это уравнение называется каноническим уравнением эллипса.

2.7.4.3. Свойства эллипса.

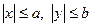
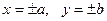
1. Из уравнения (2.25) следует, что , это означает, что график эллипса ограничен прямоугольником .

2. Так как в уравнение входят только четные степени х, у, то если точка (х, у) принадлежит эллипсу, (т.е. х, у удовлетворяют уравнению), то точки (-х, у), (х, —у), (-х, —у) тоже принадлежат уравнению. Следовательно, оси Oх и Оу являются осями симметрии эллипса, точка О(0, 0) является центром симметрии.

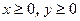
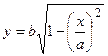
3. Рассмотрим часть эллипса, расположенную в первом квадранте ( ). Решив уравнение относительно у, получим .

Если x = 0, то у = b; если x = а, то у = 0; у убывает при возрастании х;.

На Рис. 2.18 изображен график эллипса.

1. Число а называют большой полуосью эллипса, b – малой полуосью.

2. Число называется эксцентриситетом эллипса. Этот параметр характеризует степень «сжатия» эллипса. Если (т.е. с = 0, b = а) фокусы эллипса совпадают с его центром, полуоси равны и эллипс превращается в окружность. Если ( ) эллипс вырождается в отрезок, соединяющий фокусы.

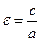
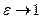
Дата добавления: 2016-04-14 ; просмотров: 2191 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Глава 32. Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей

Один из углов f между плоскостями A1x + B1y + C1z + D1 = 0 и
A2x +B2y + C2z + D2 = 0 (рис. 2.18.1) равен углу между их нормальными векторами и и определяется по формуле:

Найти угол между плоскостями x – y + 21/2z + 2 = 0 и x + y +21/2z – 3 = 0.

Условие параллельности плоскостей

Две плоскости параллельны тогда и только тогда, когда их нормальные векторы и коллинеарны, следовательно, их координаты пропорциональны, т. е.

Определить, параллельны ли плоскости 2x–3y–4z+11=0 и –4x+6y+8z+36=0.

Плоскости параллельны, так как

Условие перпендикулярности плоскостей

Если две плоскости заданы уравнениями A1x1 + B1y1 + C1z1 + D = 0, A2x2 + B2y2 + C2z2 + D = 0, то условием их перпендикулярности является

A1A2 + B1B2 + C1C2 = 0.

Если плоскости перпендикулярны, то перпендикулярны и их нормальные векторы N1 и N2.

Определить перпендикулярны ли плоскости 3x–2y–2z+7=0 и 2x+2y+z+4=0.

Так как 3×2+(–2)×2+(–2) ×1=0, то заданные плоскости перпендикулярны.

Плоскость, проходящая через данную точку параллельно данной плоскости

Плоскость, проходящая через точку M1(x1;y1;z1) и параллельная плоскости Ax+By+Cz+D=0, представляется уравнением

A(x–x1) + B(y–y1) + C(z–z1) = 0.

Написать уравнение плоскости, проходящей через точку (2;–1;6) параллельно плоскости x+y–2z+5=0.

(x–2) + (y+1) –2(z–6) = 0, т. е. x + y – 2z + 11 = 0.

Плоскость, проходящая через две точки перпендикулярно к данной плоскости

Плоскость P, проходящая через две точки M0(x0,y0,z0) и M1(x1,y1,z1) перпендикулярно к плоскости Q, заданной уравнением Ax+By+Cz+D=0, представляется уравнением

Написать уравнение плоскости, проходящей через две точки: M0(1;2;3) и M1(2;1;1) перпендикулярно к плоскости 3x+4y+z–6=0.

Плоскость представляется уравнением:

т. е. x–y+z–2=0.

Расстояние от точки до плоскости

Расстояние от точки M1(x1;y1;z1) до плоскости Ax+By+Cz+D=0 равно

Найти расстояние от точки (3;9;1) до плоскости x–2y+2z–3=0.