Даны координаты треугольника параметрическое уравнение

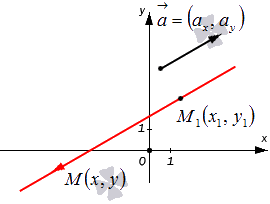
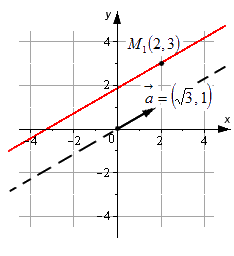
Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Параметрические уравнения прямой на плоскости: описание, примеры, решение задач

Одним из подпунктов темы «Уравнение прямой на плоскости» является вопрос составления параметрических уравнений прямой на плоскости в прямоугольной системе координат. В статье ниже рассматривается принцип составления подобных уравнений при определенных известных данных. Покажем, как от параметрических уравнений переходить к уравнениям иного вида; разберем решение типовых задач.

Вывод параметрических уравнений прямой на плоскости

Конкретная прямая может быть определена, если задать точку, которая принадлежит этой прямой, и направляющий вектор прямой.

Допустим, нам задана прямоугольная система координат O x y . А также заданы прямая а с указанием лежащей на ней точки М 1 ( x 1 , y 1 ) и направляющий вектор заданной прямой a → = ( a x , a y ) . Дадим описание заданной прямой a , используя уравнения.

Используем произвольную точку М ( x , y ) и получим вектор М 1 М → ; вычислим его координаты по координатам точек начала и конца: M 1 M → = ( x — x 1 , y — y 1 ) . Опишем полученное: прямая задана множеством точек М ( x , y ) , проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Указанное множество задает прямую только тогда, когда векторы M 1 M → = ( x — x 1 , y — y 1 ) и a → = ( a x , a y ) являются коллинеарными.

Существует необходимое и достаточное условие коллинеарности векторов, которое в данном случае для векторов M 1 M → = ( x — x 1 , y — y 1 ) и a → = ( a x , a y ) возможно записать в виде уравнения:

M 1 M → = λ · a → , где λ – некоторое действительное число.

Уравнение M 1 M → = λ · a → называют векторно-параметрическим уравнением прямой.

В координатной форме оно имеет вид:

M 1 M → = λ · a → ⇔ x — x 1 = λ · a x y — y 1 = λ · a y ⇔ x = x 1 + a x · λ y = y 1 + a y · λ

Уравнения полученной системы x = x 1 + a x · λ y = y 1 + a y · λ носят название параметрических уравнений прямой на плоскости в прямоугольной системе координат. Суть названия в следующем: координаты всех точек прямой возможно определить по параметрическим уравнениям на плоскости вида x = x 1 + a x · λ y = y 1 + a y · λ при переборе всех действительных значений параметра λ

Составление параметрических уравнений прямой на плоскости

Согласно вышесказанному, параметрические уравнения прямой на плоскости x = x 1 + a x · λ y = y 1 + a y · λ определяют прямую линию, которая задана в прямоугольной системе координат, проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Следовательно, если заданы координаты некоторой точки прямой и координаты ее направляющего вектора, то возможно сразу записать параметрические уравнения заданной прямой.

Необходимо составить параметрические уравнения прямой на плоскости в прямоугольной системе координат, если заданы принадлежащая ей точка М 1 ( 2 , 3 ) и ее направляющий вектор a → = ( 3 , 1 ) .

Решение

На основе исходных данных получим: x 1 = 2 , y 1 = 3 , a x = 3 , a y = 1 . Параметрические уравнения будут иметь вид:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 2 + 3 · λ y = 3 + 1 · λ ⇔ x = 2 + 3 · λ y = 3 + λ

Ответ: x = 2 + 3 · λ y = 3 + λ

Необходимо отметить: если вектор a → = ( a x , a y ) служит направляющим вектором прямой а, а точки М 1 ( x 1 , y 1 ) и М 2 ( x 2 , y 2 ) принадлежат этой прямой, то ее возможно определить, задав параметрическими уравнениями вида: x = x 1 + a x · λ y = y 1 + a y · λ , а также и таким вариантом: x = x 2 + a x · λ y = y 2 + a y · λ .

К примеру, нам заданы направляющий вектор прямой a → = ( 2 , — 1 ) , а также точки М 1 ( 1 , — 2 ) и М 2 ( 3 , — 3 ) , принадлежащие этой прямой. Тогда прямую определяют параметрические уравнения: x = 1 + 2 · λ y = — 2 — λ или x = 3 + 2 · λ y = — 3 — λ .

Следует обратить внимание и на такой факт: если a → = ( a x , a y ) — направляющий вектор прямой a , то ее направляющим вектором будет и любой из векторов μ · a → = ( μ · a x , μ · a y ) , где μ ϵ R , μ ≠ 0 .

Таким образом, прямая а на плоскости в прямоугольной системе координат может быть определена параметрическими уравнениями: x = x 1 + μ · a x · λ y = y 1 + μ · a y · λ при любом значении μ , отличном от нуля.

Допустим, прямая а задана параметрическими уравнениями x = 3 + 2 · λ y = — 2 — 5 · λ . Тогда a → = ( 2 , — 5 ) — направляющий вектор этой прямой. А также любой из векторов μ · a → = ( μ · 2 , μ · — 5 ) = 2 μ , — 5 μ , μ ∈ R , μ ≠ 0 станет направляющим вектором для заданной прямой. Для наглядности рассмотрим конкретный вектор — 2 · a → = ( — 4 , 10 ) , ему соответствует значение μ = — 2 . В таком случае заданную прямую можно также определить параметрическими уравнениями x = 3 — 4 · λ y = — 2 + 10 · λ .

Переход от параметрических уравнений прямой на плоскости к прочим уравнениям заданной прямой и обратно

В решении некоторых задач применение параметрических уравнений является не самым оптимальным вариантом, тогда возникает необходимость перевода параметрических уравнений прямой в уравнения прямой другого вида. Рассмотрим, как же это сделать.

Параметрическим уравнениям прямой вида x = x 1 + a x · λ y = y 1 + a y · λ будет соответствовать каноническое уравнение прямой на плоскости x — x 1 a x = y — y 1 a y .

Разрешим каждое из параметрических уравнений относительно параметра λ , приравняем правые части полученных равенств и получим каноническое уравнение заданной прямой:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y

При этом не должно смущать, если a x или a y будут равны нулю.

Необходимо осуществить переход от параметрических уравнений прямой x = 3 y = — 2 — 4 · λ к каноническому уравнению.

Решение

Запишем заданные параметрические уравнения в следующем виде: x = 3 + 0 · λ y = — 2 — 4 · λ

Выразим параметр λ в каждом из уравнений: x = 3 + 0 · λ y = — 2 — 4 · λ ⇔ λ = x — 3 0 λ = y + 2 — 4

Приравняем правые части системы уравнений и получим требуемое каноническое уравнение прямой на плоскости:

x — 3 0 = y + 2 — 4

Ответ: x — 3 0 = y + 2 — 4

В случае, когда необходимо записать уравнение прямой вида A x + B y + C = 0 , при этом заданы параметрические уравнения прямой на плоскости, необходимо сначала осуществить переход к каноническому уравнению, а затем к общему уравнению прямой. Запишем всю последовательность действий:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y ⇔ ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ A x + B y + C = 0

Необходимо записать общее уравнение прямой, если заданы определяющие ее параметрические уравнения: x = — 1 + 2 · λ y = — 3 · λ

Решение

Для начала осуществим переход к каноническому уравнению:

x = — 1 + 2 · λ y = — 3 · λ ⇔ λ = x + 1 2 λ = y — 3 ⇔ x + 1 2 = y — 3

Полученная пропорция идентична равенству — 3 · ( x + 1 ) = 2 · y . Раскроем скобки и получим общее уравнение прямой: — 3 · x + 1 = 2 · y ⇔ 3 x + 2 y + 3 = 0 .

Ответ: 3 x + 2 y + 3 = 0

Следуя вышеуказанной логике действий, для получения уравнения прямой с угловым коэффициентом, уравнения прямой в отрезках или нормального уравнения прямой необходимо получить общее уравнение прямой, а от него осуществлять дальнейший переход.

Теперь рассмотрим обратное действие: запись параметрических уравнений прямой при другом заданном виде уравнений этой прямой.

Самый простой переход: от канонического уравнения к параметрическим. Пусть задано каноническое уравнение вида: x — x 1 a x = y — y 1 a y . Каждое из отношений этого равенства примем равным параметру λ :

x — x 1 a x = y — y 1 a y = λ ⇔ λ = x — x 1 a x λ = y — y 1 a y

Разрешим полученные уравнения относительно переменных x и y :

x = x 1 + a x · λ y = y 1 + a y · λ

Необходимо записать параметрические уравнения прямой, если известно каноническое уравнение прямой на плоскости: x — 2 5 = y — 2 2

Решение

Приравняем части известного уравнения к параметру λ : x — 2 5 = y — 2 2 = λ . Из полученного равенства получим параметрические уравнения прямой: x — 2 5 = y — 2 2 = λ ⇔ λ = x — 2 5 λ = y — 2 5 ⇔ x = 2 + 5 · λ y = 2 + 2 · λ

Ответ: x = 2 + 5 · λ y = 2 + 2 · λ

Когда необходимо осуществить переход к параметрическим уравнениям от заданного общего уравнения прямой, уравнения прямой с угловым коэффициентом или уравнения прямой в отрезках, необходимо исходное уравнение привести к каноническому, а после осуществлять переход к параметрическим уравнениям.

Необходимо записать параметрические уравнения прямой при известном общем уравнении этой прямой: 4 x — 3 y — 3 = 0 .

Решение

Заданное общее уравнение преобразуем в уравнение канонического вида:

4 x — 3 y — 3 = 0 ⇔ 4 x = 3 y + 3 ⇔ ⇔ 4 x = 3 y + 1 3 ⇔ x 3 = y + 1 3 4

Приравняем обе части равенства к параметру λ и получим требуемые параметрические уравнения прямой:

x 3 = y + 1 3 4 = λ ⇔ x 3 = λ y + 1 3 4 = λ ⇔ x = 3 · λ y = — 1 3 + 4 · λ

Ответ: x = 3 · λ y = — 1 3 + 4 · λ

Примеры и задачи с параметрическими уравнениями прямой на плоскости

Рассмотрим чаще всего встречаемые типы задач с использованием параметрических уравнений прямой на плоскости в прямоугольной системе координат.

1. В задачах первого типа заданы координаты точек, принадлежащих или нет прямой, описанной параметрическими уравнениями.

Решение таких задач опирается на следующий факт: числа ( x , y ) , определяемые из параметрических уравнений x = x 1 + a x · λ y = y 1 + a y · λ при некотором действительном значении λ , являются координатами точки, принадлежащей прямой, которая описывается этими параметрическими уравнениями.

Необходимо определить координаты точки, которая лежит на прямой, заданной параметрическими уравнениями x = 2 — 1 6 · λ y = — 1 + 2 · λ при λ = 3 .

Решение

Подставим в заданные параметрические уравнения известное значение λ = 3 и осуществим вычисление искомых координат: x = 2 — 1 6 · 3 y = — 1 + 2 · 3 ⇔ x = 1 1 2 y = 5

Ответ: 1 1 2 , 5

Также возможна следующая задача: пусть задана некоторая точка M 0 ( x 0 , y 0 ) на плоскости в прямоугольной системе координат и нужно определить, принадлежит ли эта точка прямой, описываемой параметрическими уравнениями x = x 1 + a x · λ y = y 1 + a y · λ .

Чтобы решить подобную задачу, необходимо подставить координаты заданной точки в известные параметрические уравнения прямой. Если будет определено, что возможно такое значение параметра λ = λ 0 , при котором будут верными оба параметрических уравнения, тогда заданная точка является принадлежащей заданной прямой.

Заданы точки М 0 ( 4 , — 2 ) и N 0 ( — 2 , 1 ) . Необходимо определить, являются ли они принадлежащими прямой, определенной параметрическими уравнениями x = 2 · λ y = — 1 — 1 2 · λ .

Решение

Подставим координаты точки М 0 ( 4 , — 2 ) в заданные параметрические уравнения:

4 = 2 · λ — 2 = — 1 — 1 2 · λ ⇔ λ = 2 λ = 2 ⇔ λ = 2

Делаем вывод, что точка М 0 принадлежит заданной прямой, т.к. соответствует значению λ = 2 .

Далее по аналогии проверим заданную точку N 0 ( — 2 , 1 ) , подставив ее координаты в заданные параметрические уравнения:

— 2 = 2 · λ 1 = — 1 — 1 2 · λ ⇔ λ = — 1 λ = — 4

Очевидно, что не существует такого параметра λ , которому будет соответствовать точка N 0 . Другими словами, заданная прямая не проходит через точку N 0 ( — 2 , 1 ) .

Ответ: точка М 0 принадлежит заданной прямой; точка N 0 не принадлежит заданной прямой.

1. В задачах второго типа требуется составить параметрические уравнения прямой на плоскости в прямоугольной системе координат. Самый простой пример такой задачи (при известных координатах точки прямой и направляющего вектора) был рассмотрен выше. Теперь разберем примеры, в которых сначала нужно найти координаты направляющего вектора, а потом записать параметрические уравнения.

Пример 8

Задана точка M 1 1 2 , 2 3 . Необходимо составить параметрические уравнения прямой, проходящей через эту точку и параллельной прямой x 2 = y — 3 — 1 .

Решение

По условию задачи прямая, уравнение которой нам предстоит опередить, параллельна прямой x 2 = y — 3 — 1 . Тогда в качестве направляющего вектора прямой, проходящей через заданную точку, возможно использовать направляющий вектор прямой x 2 = y — 3 — 1 , который запишем в виде: a → = ( 2 , — 1 ) . Теперь известны все необходимые данные для того, чтобы составить искомые параметрические уравнения:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 1 2 + 2 · λ y = 2 3 + ( — 1 ) · λ ⇔ x = 1 2 + x · λ y = 2 3 — λ

Ответ: x = 1 2 + x · λ y = 2 3 — λ .

Задана точка М 1 ( 0 , — 7 ) . Необходимо записать параметрические уравнения прямой, проходящей через эту точку перпендикулярно прямой 3 x – 2 y – 5 = 0 .

Решение

В качестве направляющего вектора прямой, уравнение которой надо составить, возможно взять нормальный вектор прямой 3 x – 2 y – 5 = 0 . Его координаты ( 3 , — 2 ) . Запишем требуемые параметрические уравнения прямой:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 0 + 3 · λ y = — 7 + ( — 2 ) · λ ⇔ x = 3 · λ y = — 7 — 2 · λ

Ответ: x = 3 · λ y = — 7 — 2 · λ

1. В задачах третьего типа требуется осуществить переход от параметрических уравнений заданной прямой к прочим видам уравнений, которые ее определяют. Решение подобных примеров мы рассматривали выше, приведем еще один.

Пример 10

Дана прямая на плоскости в прямоугольной системе координат, определяемая параметрическими уравнениями x = 1 — 3 4 · λ y = — 1 + λ . Необходимо найти координаты какого-либо нормального вектора этой прямой.

Решение

Чтобы определить искомые координаты нормального вектора, осуществим переход от параметрических уравнений к общему уравнению:

x = 1 — 3 4 · λ y = — 1 + λ ⇔ λ = x — 1 — 3 4 λ = y + 1 1 ⇔ x — 1 — 3 4 = y + 1 1 ⇔ ⇔ 1 · x — 1 = — 3 4 · y + 1 ⇔ x + 3 4 y — 1 4 = 0

Коэффициенты переменных x и y дают нам требуемые координаты нормального вектора. Таким образом, нормальный вектор прямой x = 1 — 3 4 · λ y = — 1 + λ имеет координаты 1 , 3 4 .

Образцы выполнения некоторых заданий

Рассмотрим решения некоторых практических упражнений.

Задание 2(е)

На плоскости даны точки А(11; -5), В(6;7), С(-10; -5). Найти уравнение биссектрисы угла А.

Решение задания 2(е)

Найдем направляющий вектор биссектрисы как сумму ортов векторов и

,

или (умножая на )

.

; ;

; .

.

Таким образом, в качестве направляющего вектора биссектрисы угла А можно взять вектор и уравнение биссектрисы будет иметь вид

.

Задание 3

Дана точка (0;2) пересечения медиан треугольника и уравнения двух его сторон 5х – 4у + 15 = 0 и 4х + у – 9 = 0. Найти координаты вершин треугольника и уравнение третьей стороны.

Решение Координаты одной вершины найдем как координаты точки пересечения данных сторон, для чего решим систему уравнений

Получаем или

Точка О_ц пересечения медиан треугольника называется его центром. Отметим одно свойство центра треугольника, которое используем для нахождения координат остальных вершин:

; ,

где х_ц, у_ц – координаты центра треугольника;

х_i, y_i – координаты i-ой вершины треугольника,

Для доказательства этих формул рассмотрим треугольник А₁А₂А₃, где А_i(x_i;y_i), i = 1-3 (см.рис.2.1).

Рис.2.1. Вспомогательный чертеж к заданию 3

Пусть В середина стороны А₁А₂. Тогда А₃В – медиана треугольника А₁А₂А₃. По известному из элементарной геометрии свойству медиан треугольника .

Тогда координаты точки В найдем по формулам

и ,

а координаты центра О_ц из векторного соотношения , которое в координатной форме записывается так

, .

Отсюда, выражая х_ц и у_ц через x_i, y_i, получим требуемые формулы.

Вернемся к решению задания 3. Используя доказанные формулы, полагая в них х₁ = 1 и у₁ = 5, х_ц = 0 и у_ц = 2, получим два уравнения, которым должны удовлетворять координаты остальных двух вершин

; ,

Еще два уравнения получим, если потребуем, чтобы искомые точки, вершины треугольника, принадлежали заданным сторонам, т.е. их координаты удовлетворяли уравнениям этих сторон

Итак, для определения четырех неизвестных х₂, у₂, х₃, у₃, мы имеем четыре независимых (!) условия (уравнения)

Решив эту систему, получим х₂ = -3, у₂ = 0, х₂= 2, у₃ = 1.

Наконец, уравнение третьей стороны запишем как уравнение прямой, проходящей через две заданные точки (-3;0) и (2;1)

или .

Итак, уравнение третьей стороны x – 5у + 3 = 0, а вершины треугольника имеют координаты (1;5), (-3;0), (2;1).

Задание 7

Составить уравнение линии, для каждой точки М которой, отношение расстояний до точки F( ) и до прямой
равно .

Привести уравнение линии к каноническому виду, определить тип линии и построить линию на чертеже. Показать на чертеже фокусы, директрисы, асимптоты (если они имеются у построенной линии).

Замечание. Отметим, что в заданиях этого модуля ; ; .

Пусть n = 101. Тогда:

, т.к. ;

, т.к. ;

, т.к. .

Итак, для n = 101 первая часть задания 7 принимает вид:

Составить уравнение линии, для каждой точки М которой, отношение расстояния до точки F(-4;1) и до прямой x = 1
равно .

Решение задания 7 (для n = 101).

Пусть М(х;у) произвольная точка искомой линии, r – расстояние от М до F и d – расстояние от точки М до прямой x = 1. Тогда

и .

По условию , т.е. d = 2r.

— уравнение искомой линии.

Упростим уравнение линии и приведем его к каноническому виду. Для этого возведем обе части уравнения в квадрат и выполним следующие преобразования уравнения

х 2 – 2х +1 = 4х 2 + 32х + 64 + 4(у – 1) 2 ,

3х 2 + 34х + 4(у – 1) 2 + 63 = 0,

,

.

Последнее уравнение – это каноническое уравнение эллипса с полуосями и ( ), центр которого находится в точке с координатами . Координаты вершин эллипса
и , т.е. (-9;1), , ,
. Построим эллипс на чертеже (см.рис.2.2).

Рис.2.2. Эллипс с уравнением

Фокусы эллипса имеют координаты , где .

.

Итак, координаты фокусов F₁(-4;1), F₂( ;1).

Директрисы эллипса имеют уравнения , где е – эксцентриситет эллипса

.

Уравнения директрис , т.е.

D₂: .

Отметим фокусы и директрисы эллипса на рис.2.2.

Обратите внимание на совпадение фокуса F₁ с точкой, данной в условии задания 7, на совпадение директрисы D₁ с прямой х = 1 из условия этого задания, и совпадение эксцентриситета е с параметром е в условии. По этому поводу см. теоретическое упражнение 18.

В пространстве даны точки А(-2; -4;1), В(3;1; -1), С(5;1;1),
S(1;-4;0). Найти координаты центра и радиус вписанной в пирамиду SABC сферы (условие сформулировано для n = 101).

Решение задания 4(м)

Пусть точка О(x₀;y₀;z₀) – центр сферы, вписанной в пирамиду SABC. Найдем точку О как точку, равноудаленную от граней пирамиды. Для этого найдем уравнения всех граней и расстояния от точки О до этих граней (уравнения некоторых граней находятся в предшествующих пункту М пунктах задания 4).

Грань АВС. Уравнение грани

или 5х – 7у – 5z – 13 = 0.

Точки О и S лежат по одну сторону от грани АВС, поэтому отклонения этих точек от грани АВС имеют одинаковые знаки. Отклонение (S) точки S от грани АВС равно

> 0.

.

Аналогично все делается для граней ABS, BCS, CAS.

Грань ABS имеет уравнение 5х + у + 15z – 1 = 0 и
.

Грань BCS имеет уравнение 5х – 3у – 5z – 17 = 0 и
.

Наконец, грань CAS имеет уравнение 5х – 7у + 15z + 33 = 0 и
.

Так как О – центр сферы, вписанной в пирамиду SABC, то

d(O; ABC) = d(O; ABS) = d(O; BCS) = d(O; CAS) = r,

где r – радиус вписанной сферы.

Тогда координаты точки О должны удовлетворять системе

В отличие от других заданий этого модуля, коэффициенты и решение этой системы найдем приближенно, с помощью микрокалькулятора или ЭВМ. Получим систему

и уравнение вписанной сферы

.

1. Общее уравнение прямой на плоскости. Нормальный вектор прямой. Угол между прямыми. Условия параллельности и перпендикулярности.

2. Уравнение прямой с угловым коэффициентом. Угол между прямыми. Условия параллельности и перпендикулярности.

3. Каноническое и параметрическое уравнения прямой на плоскости. Направляющий вектор прямой. Угол между прямыми. Условия параллельности и перпендикулярности.

4. Уравнение прямой, проходящей через две заданные точки.

5. Уравнения прямых, проходящих через данную точку параллельно и перпендикулярно данной прямой (3 случая задания данной прямой: общим уравнением, каноническим уравнением, уравнением с угловым коэффициентом).

6. Общее уравнение плоскости в пространстве, нормальный вектор плоскости. Угол между плоскостями. Условие параллельности и перпендикулярности.

7. Уравнение плоскости, проходящей через три данные точки, не лежащие на одной прямой.

8. Общее, каноническое и параметрическое уравнения прямой в пространстве. Угол между прямыми. Условия параллельности и перпендикулярности.

9. Угол между прямой и плоскостью в пространстве. Условие параллельности и перпендикулярности прямой и плоскости.

10. Уравнение плоскости, проходящей через данную точку, перпендикулярно данной прямой. Уравнение прямой, проходящей через данную точку, перпендикулярно данной плоскости.

11. Расстояние от точки до: прямой на плоскости; прямой в пространстве; плоскости в пространстве.

12. Уравнение линии на плоскости. Общее уравнение кривой второго порядка.

13. Каноническое и параметрическое уравнения окружности.

14. Эллипс (фокусы и директрисы, фокальные радиусы точки, эксцентриситет). Каноническое и параметрическое уравнения эллипса.

15. Гипербола (фокусы, директрисы и асимптоты, фокальные радиусы точки, эксцентриситет). Каноническое и параметрическое уравнения гиперболы.

16. Парабола (фокус и директриса, фокальный радиус точки, эксцентриситет). Каноническое уравнение параболы.

17. Приведение общего уравнения кривой второго порядка к каноническому виду.

18. Полярные координаты на плоскости. Уравнение линии в полярных координатах.

19. Уравнение поверхности в пространстве. Общее уравнение поверхностей второго порядка.

20. Основные типы поверхностей второго порядка и их канонические уравнения.

1. Бугров Н.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – М.: Наука, 1980. 176 с.

2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.1: Учебное пособие для студентов втузов. – 3-е изд., перераб. и доп. – М.: Высшая школа, 1980. 320 с.

3. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Наука, 1981. 232 с.

4. Клетеник Д.В. Сборник задач по аналитической геометрии. – М.: Наука, 1980. 240 с.

5. Сборник задач по математике для втузов. Линейная алгебра и основы математического анализа/Под ред. А.В. Ефимова, Б.П. Демидович. – М.: Наука, 1981, 464 с.

6. Высшая математика. Методические указания и контрольные задания/Под ред. Ю.С. Арутюнова. – М.: Высшая школа, 1985.

7. Гусак А.А. Пособие к решению задач по высшей математике. – Изд. 3-е. – Минск: Изд-во БГУ, 1973. 532 с.

8. Кузнецов А.А. Сборник заданий по высшей математике (типовые расчеты): Учеб. пособие для втузов. – М.: Высшая школа, 1983. 175 с.

9. Погорелов А.В.Аналитическая геометрия.– М.:Наука, 1968. 176с