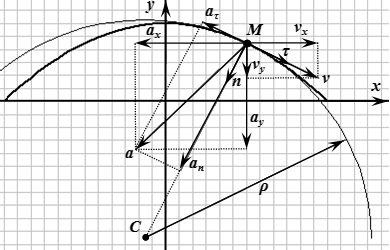
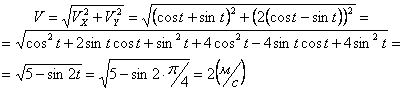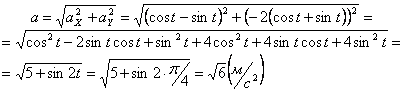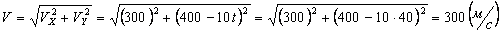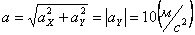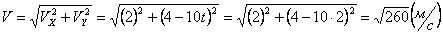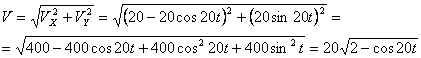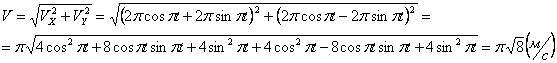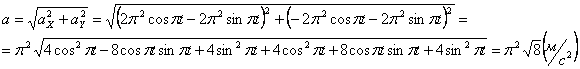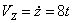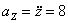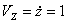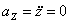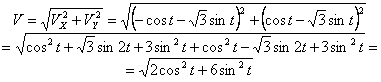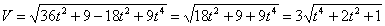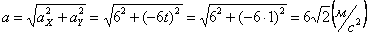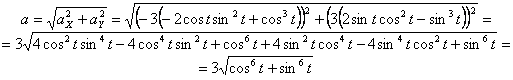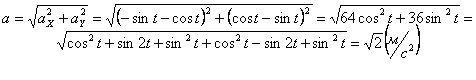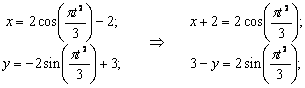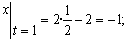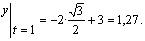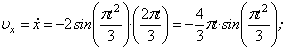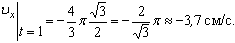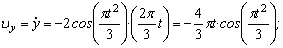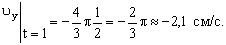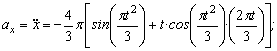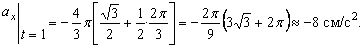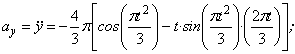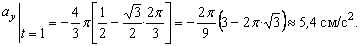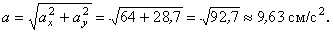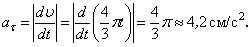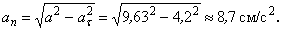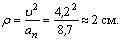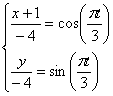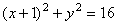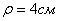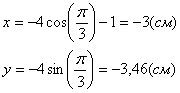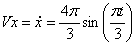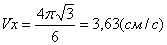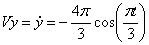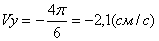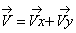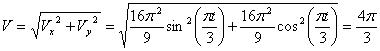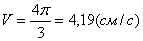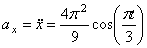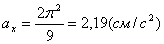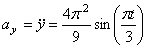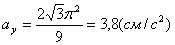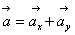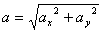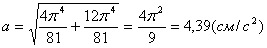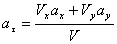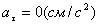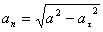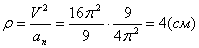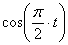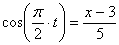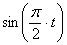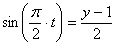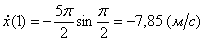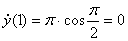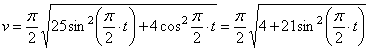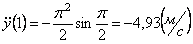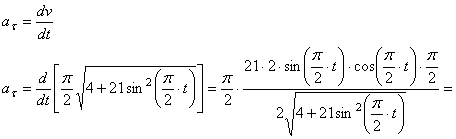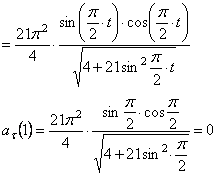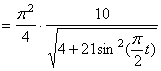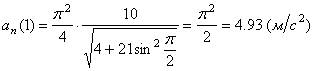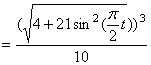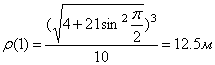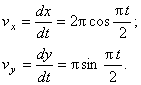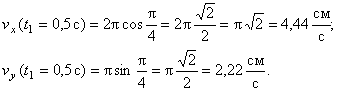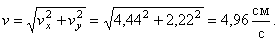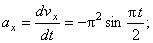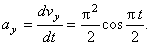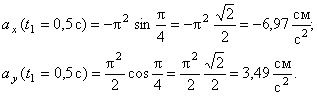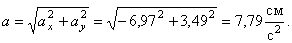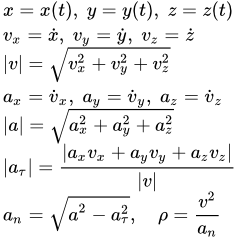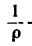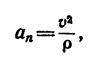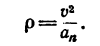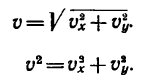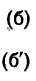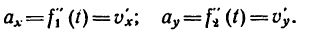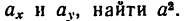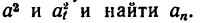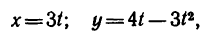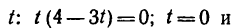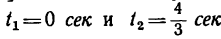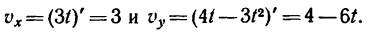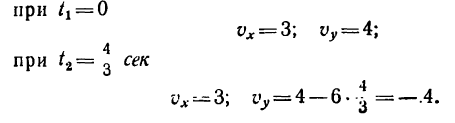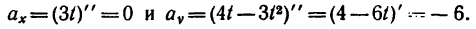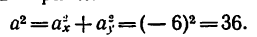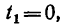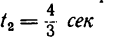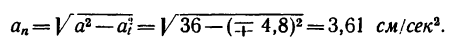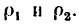Даны уравнения движения точки найти радиус кривизны
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ
7.1. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 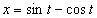
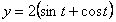
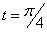
Решение: Скорости точки :
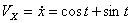
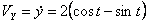
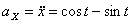
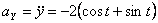
Модуль полного ускорения:
Модуль касательного ускорения точки:
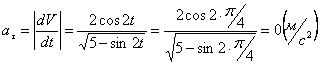
А модуль нормального ускорения:
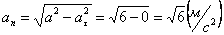
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
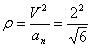
7.2. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 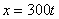
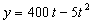
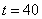
Решение: Скорости точки :
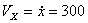
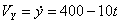
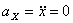
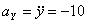
Модуль полного ускорения:
Модуль касательного ускорения точки:

А модуль нормального ускорения:
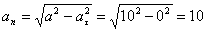
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
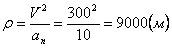
7.3. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 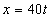
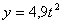
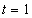
Решение: Скорости точки:
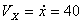
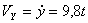
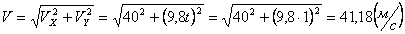
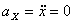
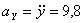
Модуль полного ускорения:
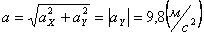
Модуль касательного ускорения точки:
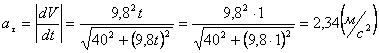
А модуль нормального ускорения:
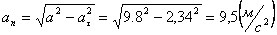
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
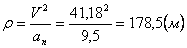
7.4. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 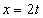
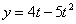
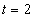
Решение: Скорости точки :
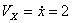
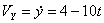
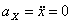
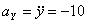
Модуль полного ускорения:
Модуль касательного ускорения точки:
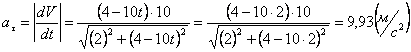
А модуль нормального ускорения:
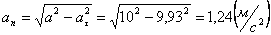
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
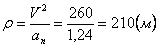
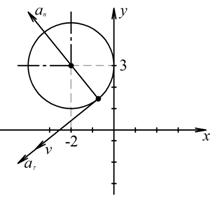
7.5. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 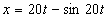
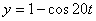
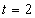
Решение: Скорости точки по осям :
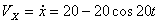
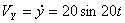
Ускорения точки по осям:
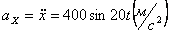
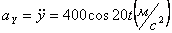
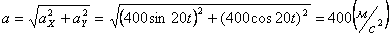
Модуль касательного ускорения точки:
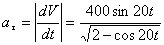
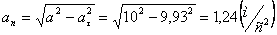
Нормальное ускорение и радиус кривизны траектории связаны соотношением 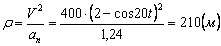
7.6. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 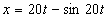
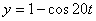

Решение: Скорости точки по осям :
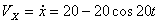
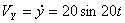
Ускорения точки по осям:
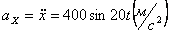
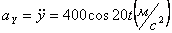
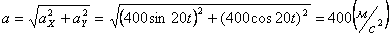
Модуль касательного ускорения точки:
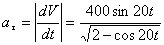
а модуль нормального ускорения:
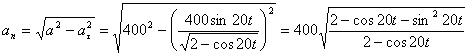
Нормальное ускорение и радиус кривизны траектории связаны соотношением 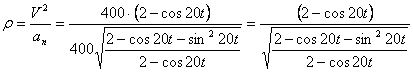
7.7. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 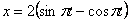
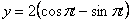
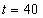
Решение: Скорости точки :
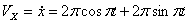
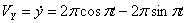
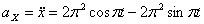
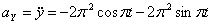
Модуль полного ускорения:
Модуль касательного ускорения точки:
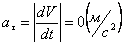
А модуль нормального ускорения:
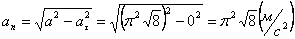
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
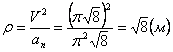
7.8. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 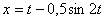
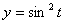

Решение: Скорости точки :
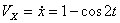
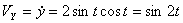
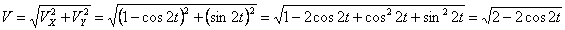
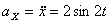
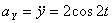
Модуль полного ускорения:
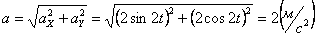
Модуль касательного ускорения точки:
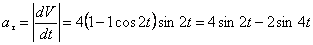
А модуль нормального ускорения:
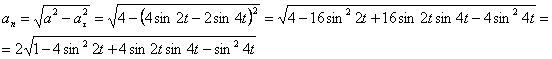
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
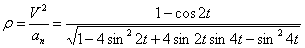
7.9. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 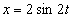
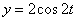
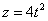
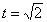
Решение: Скорости точки :
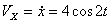
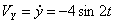
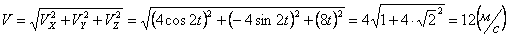
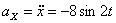
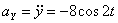
Модуль полного ускорения:
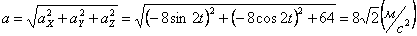
Модуль касательного ускорения точки:
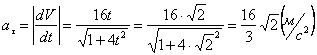
А модуль нормального ускорения:
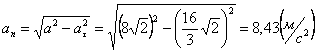
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
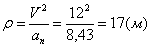
7.10. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 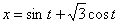
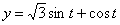
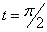
Решение: Скорости точки :
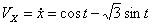
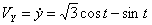
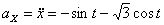
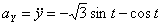
Модуль полного ускорения:
Модуль касательного ускорения точки:
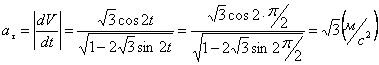
А модуль нормального ускорения:
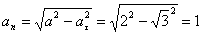
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
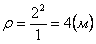
7.11. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 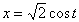
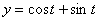
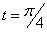
Решение: Скорости точки :
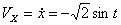
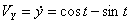
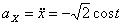
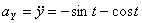
Модуль полного ускорения:
Модуль касательного ускорения точки:
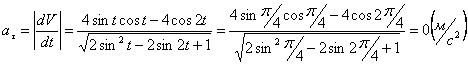
А модуль нормального ускорения:
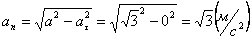
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
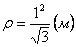
7.12. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 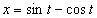
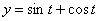
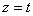

Решение: Скорости точки :
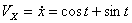
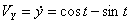
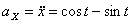
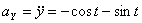
Модуль полного ускорения:
Модуль касательного ускорения точки:
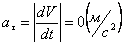
А модуль нормального ускорения:
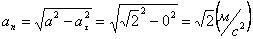
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
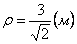
7.13. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 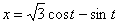
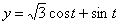

Решение: Скорости точки :
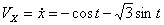
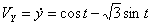
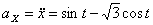
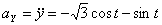
Модуль полного ускорения:
Модуль касательного ускорения точки:
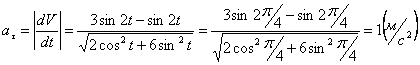
А модуль нормального ускорения:
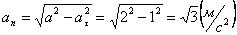
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
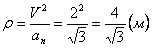
7.14. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 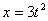
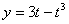
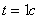
Найти: 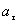
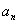
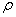
Решение: Скорости точки по осям :
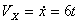
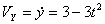
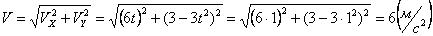
Ускорения точки по осям:
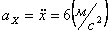
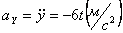
Модуль касательного ускорения точки:
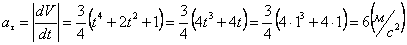
А модуль нормального ускорения:
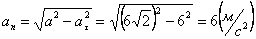
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
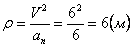
7.15. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 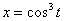
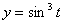

Решение: Скорости точки :
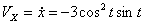
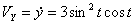
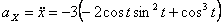
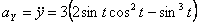
Модуль полного ускорения:
Модуль касательного ускорения точки:
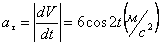
А модуль нормального ускорения:
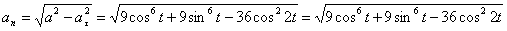
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
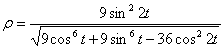
7.16. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 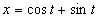
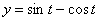

Решение: Скорости точки :
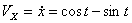
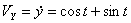
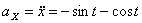
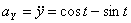
Модуль полного ускорения:
Модуль касательного ускорения точки:
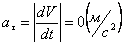
А модуль нормального ускорения:
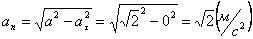
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
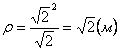
7.17. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 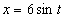
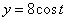
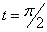
Решение: Скорости точки :
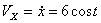
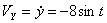
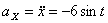
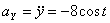
Модуль полного ускорения:
Модуль касательного ускорения точки:
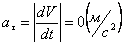
А модуль нормального ускорения:
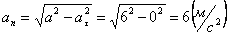
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
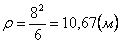
7.18. Дан закон движения точки по окружности радиусом r . Определить:
1) скорость и ускорение точки при 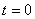

2) моменты остановки точки;
3) путь, пройденный точкой за 10секунд.
Дано: 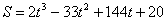
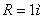
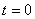

Найти: 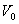
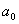
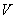
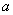
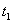
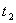
Решение: 1. На траектории отметим точку О – начало отсчета координаты s и укажем положительное направление отсчета этой координаты. Отметим положение точки в заданные моменты времени: При 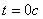
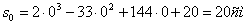
При 
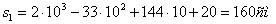
Проведем из этих точек естественные оси координат.
Определим проекцию скорости на касательную:
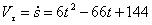
При 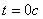
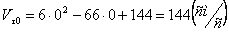
При 
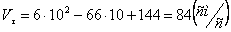
Векторы 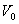
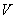
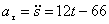
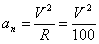
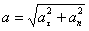
При 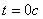
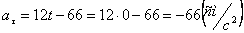
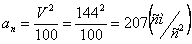
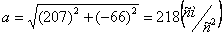
При 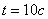
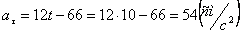
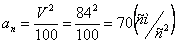
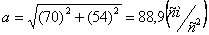
2. Чтобы найти время остановки надо найти время, когда скорость точки равна нулю:
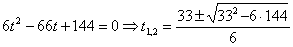
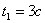
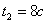
3. Поскольку за 10 секунд точка сделала две остановки, пройденный ею путь за 10с можно найти как сумму пути, пройденного от начала до первой остановки, от первой до второй остановки и от второй до момента времени 
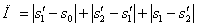
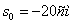
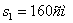
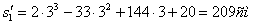
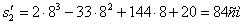
Путь пройденный точкой за 10 секунд:
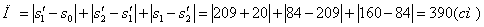
7.19. Определить скорость, касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 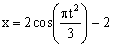
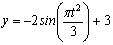
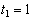
Найти: 1) вид траектории;
2) для t = t 1 положение точки на траектории;
3) 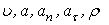
Решение: 1) Уравнение движения (1) можно рассматривать как параметрические уравнения траектории точки. Чтобы получить уравнения траектории в координатной форме, исключаем время t из уравнений (1).
Возводя обе части равенств в квадрат, а затем складывая равенства, получаем 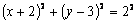
2) Определяем положение точки М в заданный момент времени t =1 с :
Вектор скорости точки
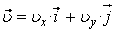
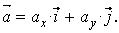
Здесь 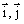
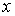
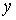
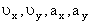
Найдем их, дифференцируя по времени уравнения движения (1):
По найденным проекциям определяем модуль скорости:
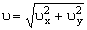
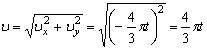
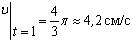
и модуль ускорения точки:
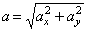
Модуль касательного ускорения точки
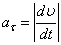
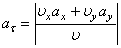
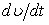
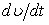
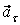
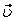
Вычисляем модуль касательного ускорения для заданного момента времени
Модуль нормального ускорения точки
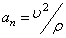
Если радиус кривизны траектории 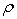
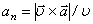
При движении точки в плоскости формула (9) принимает вид
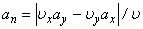
Модуль нормального ускорения можно определить и следующим образом:
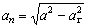
Воспользуемся в нашем случае формулой (10)
Радиус кривизны траектории в рассматриваемой точке определим из выражения:
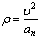
Тогда
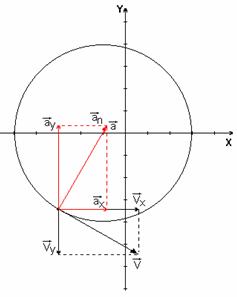
На рис. 1 показано положение точки М в заданный момент времени. Вектор 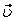
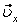
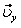
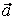
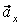
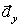
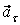
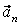
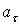
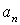
7.20. Определить скорость, касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
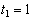
Найти: 1) вид траектории;
2) 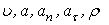
Указания. Задача — относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения. В задаче все искомые величины нужно определить только для момента времени t 1 = 1 с .
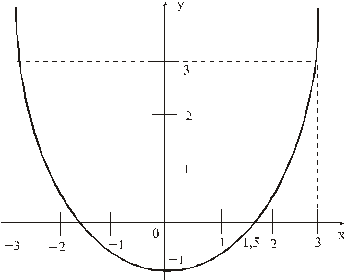
1. Для определения уравнения траектории точки исключим из заданных уравнений движения время t :
Отсюда окончательно находим уравнение траектории точки (параболы, см. рисунок):
2. Скорость точки найдем по ее проекциям на координатные оси:
V = 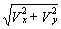
3. Аналогично найдем ускорение точки:
а =
4. Касательное ускорение найдем, дифференцируя по времени равенство:
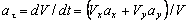
ч исловые значения всех величин, входящих в правую часть выражения (3), определены и даются равенствами (1) и (2).
Подставив в (3) эти числа, найдем сразу, что при t 1 = 1 с
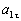
5. Нормальное ускорение точки:
a n = 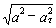
Подставляя сюда найденные числовые значения a 1 и a 1 τ , получим, что при t 1= 1 с
6. Радиус кривизны траектории ρ = V 2 / a n .
Подставляя сюда числовые значения V 1 и a 1 n , найдем, что при t 1 = 1 с
Ответ: V 1= 8 ,54 см/с, а 1 =8 см/с 2 , 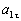
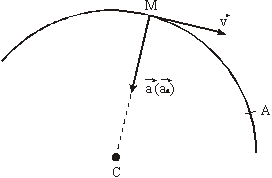
7.21. Точка движется по дуге окружности радиуса R =1 м по закону 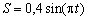
Найти: скорость и ускорение точки в момент времени t 1 =1 с .
Определяем скорость точки:
V = ds / dt = 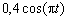
При t 1 =1 с получим 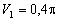
Ускорение находим по его касательной и нормальной составляющим:
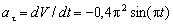
п ри t 1 = 1 с получим , учтя, что R = 1 м
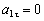
тогда ускорение точки при t 1 =1 с будет:
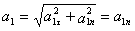
Изобразим на рисунке векторы 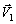
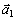
7.22. По заданным уравнениям движения точки М установить вид её траектории и для момента времени t = t 1(с) найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а так же радиус кривизны траектории.
Дано: 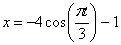
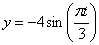
Найти: 1) вид траектории;
2) 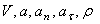
1) Найдём траекторию движения:
Для этого исключим параметр t .
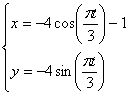
Возведём во вторую степень, получившиеся уравнения, а затем сложим, таким образом, исключится t . Получим:
Это окружность с центром в точке с координатами (-1;0) и радиусом
2) Найдём положение точки на траектории в момент времени t = t 1:
3) Определим скорость токи:
Для нахождения вектора полной скорости необходимо сложить 2 вектора:
Найдём модуль полной скорости:
для момента времени t 1:
4) Определим ускорение точки:
для момента времени t 1:
для момента времени t 1:
Найдём полное ускорение:
Найдём модуль полного ускорения:
для момента времени t 1:
Определим касательное ускорение 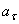
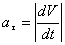
для момента времени t :
Определим нормальное ускорение an :
для момента времени t 1:
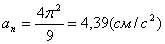
5) Из полученных результатов можно найти радиус кривизны траектории 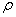
Действительно, этот радиус совпадает с радиусом окружности (траектории).
7.23. Точка М движется согласно уравнений 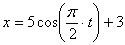
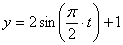
1) Найдем уравнение траектории точки. Для определения уравнения траектории исключим из уравнений движения время 
Из второго уравнения движения найдем
Возведя полученные значения ( правую и левую стороны уравнения ) в квадрат и складывая их находим:
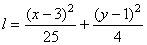
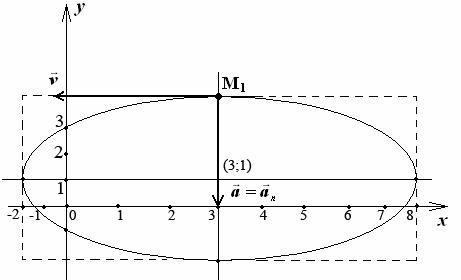
Следовательно, траекторией точки является эллипс с центром в точке с координатами (3;1).
Вид траектории показан на рисунке.
2) Найдем положение точки в момент времени t =1с
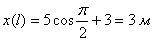
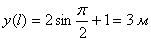
Положение точки М 1 показано на рисунке.
3) Найдем скорость точки М
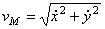
Где 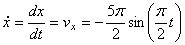
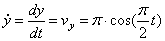
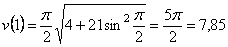
4) Найдём ускорение точки.
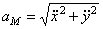
где 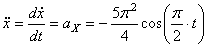
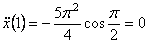
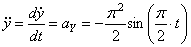
5) Найдем касательное ускорение точки M,
6) Найдём нормальное ускорение точки M ,
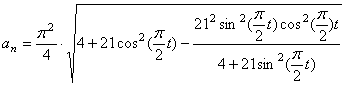
7) Найдем радиус кривизны траектории точки М,
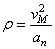
Направление векторов показано на рисунке.
Ответ: 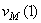
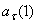
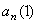
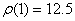
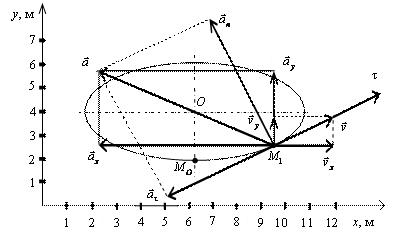
7.24. Пусть точка М движется в плоскости xOy в соответствии с уравнениями 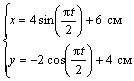
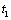
Решение: Заданный закон движения точки в координатной форме можно рассматривать как параметрические уравнения траектории точки. Исключим время t из уравнений движения и получим уравнение траектории точки в виде:
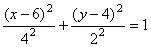
Таким образом, траекторией точки М является эллипс со смещенным центром, изображенный на рис. Отметим на траектории положение точки М 1 ( x 1, y 1) в момент времени t 1 = 0,5 c
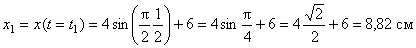
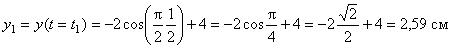
Вектор скорости точки представим в виде:
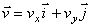
где 
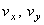
В момент времени t 1 = 0,5 c
Вектор скорости точки 
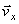
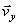
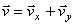
Полученный вектор должен быть направлен по касательной к траектории точки в сторону движения. Модуль скорости точки определим по уже найденным проекциям
Вектор ускорения точки представим в виде:
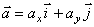
где 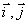
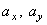
В момент времени t 1 = 0,5 c
Вектор ускорения точки 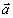
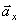
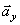
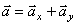
Полученный вектор ускорения точки в общем случае должен отклоняться от вектора скорости в сторону вогнутости траектории, а при движении по эллипсовидной траектории – проходить через центр эллипса. Модуль ускорения точки определим по уже найденным проекциям
Вектор полного ускорения точки можно также представить в виде геометрической суммы его проекций на оси естественной системы отсчета
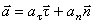
где 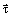
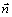
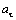
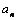
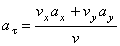
В момент времени t 1 = 0,5 c
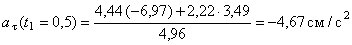
Значение касательного ускорения 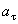
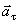
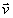
Нормальное ускорение 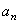
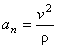
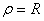
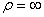
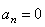
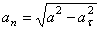
В момент времени t 1 = 0,5 c
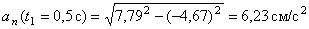
Построим векторы 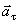
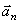
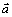
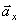
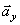
Радиус кривизны траектории в рассматриваемой точке определим по формуле
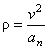
В момент времени t 1 = 0,5 c
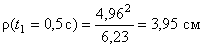
Ответ: 
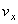
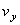
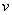
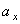
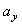
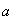
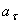
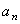
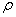
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Координатный способ задания движения точки
Введение
Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы применим основные результаты этой теории к координатному способу задания движения материальной точки.
Пусть мы имеем неподвижную прямоугольную систему координат с центром в неподвижной точке . При этом положение точки M однозначно определяются ее координатами (x, y, z). Координатный способ задания движения точки – это такой способ, при котором заданы зависимости координат от времени. То есть заданы три функции от времени (при трехмерном движении):
Далее мы приводим формулы вычисления кинематических величин и пример решения задачи для координатного способа задания движения.
Определение кинематических величин
Зная зависимости координат от времени , мы автоматически определяем радиус-вектор материальной точки M по формуле:
,
где – единичные векторы (орты) в направлении осей x, y, z .
Дифференцируя по времени , находим проекции скорости и ускорения на оси координат:
;
;
Модули скорости и ускорения:
;
.
Единичный вектор в направлении касательной к траектории:
.
Его можно определить двумя способами – по направлению скорости, или в противоположную сторону. Поэтому здесь в знаменателе стоит не модуль скорости, а алгебраическая величина скорости, которая, по абсолютной величине, равна модулю скорости, но может принимать как положительные, так и отрицательные значения: . Она является проекцией скорости на направление единичного вектора .
Алгебраическая величина тангенциального (касательного) ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории:
.
Вектор тангенциального (касательного) ускорения:
.
Здесь также, как и для скорости, – это скалярная величина, которая может принимать как положительные так и отрицательные значения: .
Нормальное ускорение:
.
Вектор нормального ускорения:
; .
Единичный вектор в направлении главной нормали траектории (то есть единичный вектор, перпендикулярный касательной и направленный к центру кривизны траектории):
.
Здесь – это модуль нормального ускорения: . Нормальное ускорение всегда направлено к центру кривизны траектории. Оно не может быть направлено в противоположную сторону.
Радиус кривизны траектории:
.
Центр кривизны траектории:
.
Единичный вектор в направлении бинормали:
.
Пример решения задачи
Определение скорости и ускорения точки по заданным уравнениям ее движения
По заданным уравнениям движения точки установить вид ее траектории и для момента времени найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Уравнения движения точки:
, см;
, см.
Решение
Определение вида траектории
Исключаем время из уравнений движения. Для этого перепишем их в виде:
; .
Применим формулу:
.
;
;
;
.
Итак, мы получили уравнение траектории:
.
Это уравнение параболы с вершиной в точке и осью симметрии .
Поскольку
, то
; или
.
Аналогичным образом получаем ограничение для координаты :
;
;
Таким образом, траекторией движения точки является дуга параболы
,
расположенная при
и .
Строим параболу по точкам.
| 0 | 6 |
| ± 3 | 5,625 |
| ± 6 | 4,5 |
| ± 9 | 2,625 |
| ± 12 | 0 |
Определяем положение точки в момент времени .
;
.
Определение скорости точки
Дифференцируя координаты и по времени , находим компоненты скорости.
.
Чтобы продифференцировать , удобно применить формулу тригонометрии:
. Тогда
;
.
Вычисляем значения компонент скорости в момент времени :
;
.
Модуль скорости:
.
Определение ускорения точки
Дифференцируя компоненты скорости и по времени , находим компоненты ускорения точки.
;
.
Вычисляем значения компонент ускорения в момент времени :
;
.
Модуль ускорения:
.
Алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории. Выберем направление совпадающим с направлением скорости . Тогда ; алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление скорости :
.
Поскольку , то вектор тангенциального ускорения направлен противоположно скорости .
Нормальное ускорение:
.
Вектор и направлен в сторону центра кривизны траектории.
Радиус кривизны траектории:
.
Траекторией движения точки является дуга параболы
; .
Скорость точки: .
Ускорение точки: ; ; .
Радиус кривизны траектории: .
Определение остальных величин
При решении задачи мы нашли:
вектор и модуль скорости:
; ;
вектор и модуль полного ускорения:
; ;
тангенциальное и нормальное ускорения:
; ;
радиус кривизны траектории: .
Определим остальные величины.
Единичный вектор в направлении касательной к траектории:
.
Вектор тангенциального ускорения:
.
Вектор нормального ускорения:
.
Единичный вектор в направлении главной нормали:
.
Координаты центра кривизны траектории:
.
Введем третью ось системы координат перпендикулярно осям и . В трехмерной системе
; .
Единичный вектор в направлении бинормали:
.
Автор: Олег Одинцов . Опубликовано: 22-02-2016 Изменено: 29-01-2020
Кинематический способ определения радиуса кривизны траектории в теоретической механике
Кинематический способ определения радиуса кривизны траектории:
При решении многих технических задач возникает необходимость знать радиус кривизны р (или
Отсюда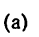
Скорость 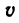
Следовательно,
Числовое значение нормального ускорения а„ входит в выражение полного ускорения точки
откуда 
где квадрат полного ускорения 
и касательное ускорение
Таким образом, если закон движения точки задан уравнениями
то при определении радиуса кривизны траектории рекомендуется произвести следующее:
1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:
2. Подставив в (б’) выражения 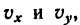
3. Продифференцировав по t уравнение (б), полученное непосредственно из (б’), найти касательное ускорение 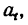
4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения
5. Подставив в (г) выражения
6. Подставить в (в) значения
7. Подставив в (а) найденные значения 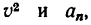
Задача:
Движение точки задано уравнениями
(х, у—в см, t — в сек). Определить радиус кривизны траектории в те моменты, когда она пересекает ось Ох.
1. В те моменты, когда траектория пересекает ось Ох, ордината у—0. Поэтому, подставив во второе уравнение движения значение у = 0, получим
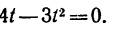
Отсюда [решая уравнение относительно 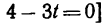
2. Находим выражения проекций скорости:
Как видно, проекция скорости на ось Ох — постоянная величина (не зависит от времени).
3. Определяем значение этих проекций в моменты пересечения траекторией оси Ох:
4. Числовое значение скорости точки в моменты пересечения траекторией оси Ох в данном случае одинаковы
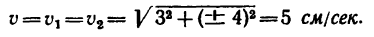
5. Находим касательное ускорение точки. Для этого получим общее выражение (уравнение) скорости, воспользовавшись зависимостью (б):
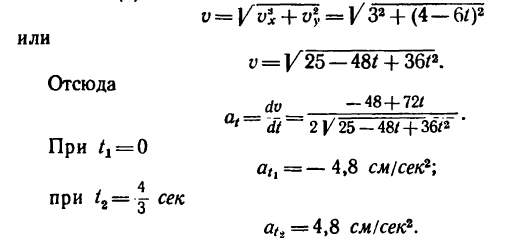
6. Находим проекции полного ускорения точки:
Следовательно, в данном случае полное ускорение точки — постоянная величина. Причем
7. Определяем нормальное ускорение точки. Как при
так и при
8. Зная, что в моменты пересечения траекторией оси 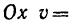
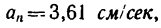
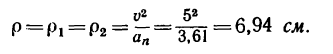
Решение этой задачи рекомендуется самостоятельно иллюстрировать чертежом, изобразив на нем траекторию точки, векторы скорости 
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Равномерное вращательное движение
- Равнопеременное вращательное движение
- Неравномерное вращательное движение
- Плоскопараллельное движение тела
- Равномерное криволинейное движение точки
- Равнопеременное движение точки
- Неравномерное движение точки по любой траектории
- Определение траектории, скорости и ускорения точки
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://1cov-edu.ru/mehanika/kinematika/tochki/koordinatnyj-sposob-zadaniya-dvizheniya/
http://www.evkova.org/kinematicheskij-sposob-opredeleniya-radiusa-kriviznyi-traektorii-v-teoreticheskoj-mehanike