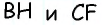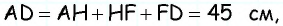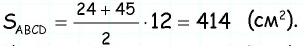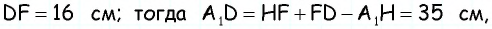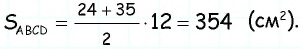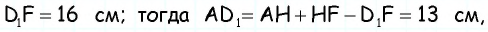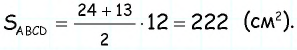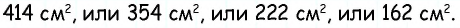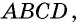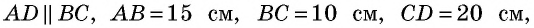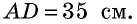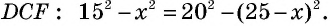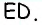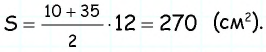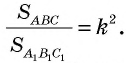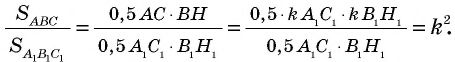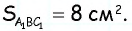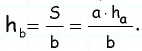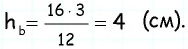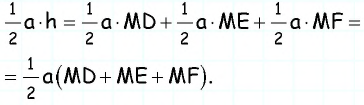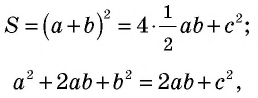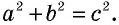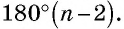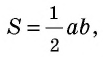Даны уравнения сторон квадрата найти площадь

Задача 34286 Пусть прямая l1(4x–y+1=0) одна из.

Условие

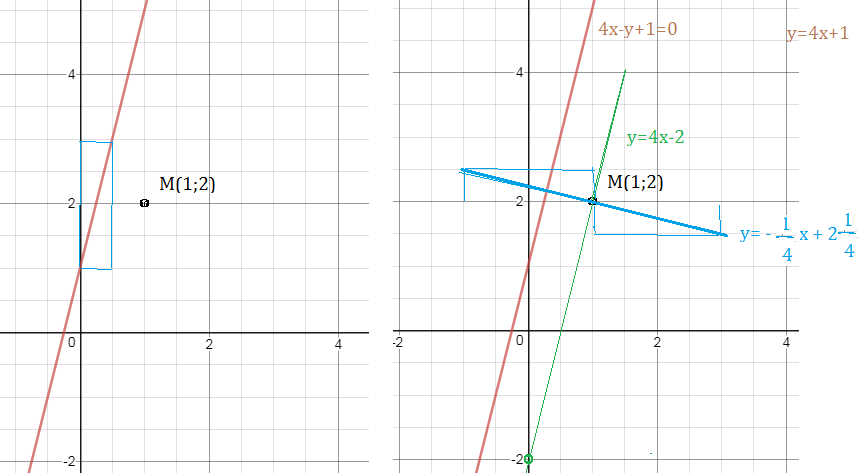
Пусть прямая l1(4x–y+1=0) одна из сторон квадрата, а точка M(1;2) его вершина. Составить уравнение остальных сторон квадрата

Решение

Расстояние d от точки M(1;2) до прямой 4х-у+1=0
это длина стороны квадрата

Уравнение прямой 4x-y+1=0 можно записать
y=4x+1
k=4
k=tg α ;
Значит прямая c угловым коэффициентом 4 — это диагональ прямоугольника, размеры 1 × 4 ( длина 1, высота 4: tgα=4/1)

Параллельная ей прямая проходит через точку М
k=4
y=4x+m
Чтобы найти m подставляем координаты точки M
2=4*1+m
m=-2

Перпендикулярная ей прямая имеет угловой k=-1/4
(потому что произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1))

Чтобы найти b подставляем координаты точки M
2=(-1/4)*1+b
b=2 целых 1/4

[b]y=(-1/4)x + 2 целых 1/4⇒ 4y+x-9=0[/b]

Третья сторона имеет угловой коэффициент k=(-1/4) и находится на расстоянии 3/sqrt(17) от точки M (1;2)

9-4n=-3 или 9-4n=3
n=3 или n=3/2
[b]4y+x-12 =0[/b] или [b]4y+x-6=0[/b]

О т в е т. [b]y=4x-2[/b]; [b]4y+x-9=0[/b]; [b]4y+x-12 =0[/b] (или [b] 4y+x-6=0[/b])

Помогите, пожалуйста, решить задачу по геометрии.

1. Даны две противоположные вершины квадрата А (1;3) и С (-1;1). Найти коорди-наты В и D.

2.Две стороны параллелограмма заданы уравнениями у = х — 2 и 5у = х + 6. Его диа-гонали пересекаются в начале координат. Написать уравнения диагоналей.

1) Уравнение диагонали АС:
(у-ус) /(уА-уС) = (х-хС) /(хА-хС)
(у-1)/2 = (х+1)/2
у = х+2
Диагональ BD перпендикулярна АС (угловой коэффициент равен -1) и проходит через середину АС, т. е. через точку О (0;2).
Уравнение диагонали BD
y = 2 — х
Искомые координаты вершин могут быть найдены, например, из условий
АO=OВ и AO=OD
(1-0)^2 + (3-2)^2 = x^2 + (2-x-2)^2
2 = 2*x^2
x = 1; y = 2-1=1 — координаты т. В
x = -1; y = 2+1 = 3 — координаты т. D
2) Одна из вершин параллелограмма — точка пересечения данных прямых. Решение системы линейных уравнений
у = х — 2
х = 5*у — 6
даст точку вершины с координатами А (4; 2).
Начало координат — точка пересечения диагоналей, поэтому противоположная вершина С (-4; -2) — центрально симметрична точке А относительно начала координат.
Собственно, сразу можно было найти уравнение диагонали АС (то же, что и прямой АО) :
у = 2*х/4 = х/2
Для нахождения второй диагонали достаточно найти третью вершину параллелограмма, например, как точку пересечения стороны, задаваемой уравнением
х = 5*у — 6
и стороны, параллельной прямой
у = х — 2
и проходящей через точку С.
уравнение этой стороны будет иметь вид:
у = -2 + х + 4
у = х + 2
Координаты вершины В найдем из решения системы:
х = 5*у — 6
у = х + 2
Вершина В (-1; 1)
Уравнение диагонали BD (то же, что и прямой ОВ)
у = -х

Решение задач на вычисление площадей с примерами вычисления и определения

Решение задач на вычисление площадей многоугольников чаще всего сводится к поиску величин отдельных элементов рассматриваемых фигур и дальнейшему применению соответствующих формул площадей.

Во многих задачах наряду с сугубо геометрическими приемами решения (дополнительные построения, применение равенства фигур и т. п.) используются и методы алгебры (составление уравнений или систем уравнений на основе метрических соотношений между элементами фигуры).

В ходе решения особое внимание следует уделить тому, однозначно ли данные задачи определяют взаимное расположение элементов фигуры.

Пример:

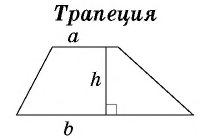
Найдите площадь трапеции, в которой одно из оснований равно 24 см, высота 12 см, а боковые стороны — 13 см и 20 см.

Решение:

Пусть

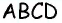
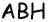
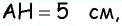
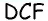
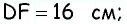
1) Для трапеции (рис. 152, а): из треугольника по теореме Пифагора имеем аналогично из треугольника имеем тогда

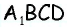
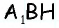
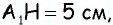
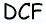
2) Для трапеции (рис. 152, б): из треугольника по теореме Пифагора имеем аналогично из треугольника имеем

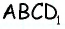
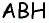
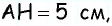
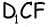
3) Для трапеции (рис. 152, в): из треугольника по теореме Пифагора имеем аналогично из треугольника имеем

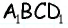
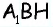
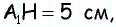
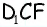
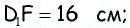
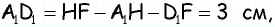
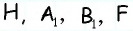
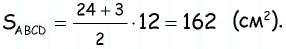
4) Для трапеции (рис. 152, г): из треугольника по теореме Пифагора имеем аналогично из треугольника имеем тогда т.е. точки расположены на прямой в указанном порядке.

Ответ:

Рассмотренная задача наглядно демонстрирует одну из причин, по которым в процессе решения геометрической задачи может возникать многовариантность. Но даже если такая ситуация не возникает, взаимное расположение элементов фигур нуждается в обосновании.

Пример:

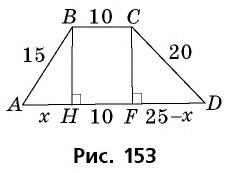
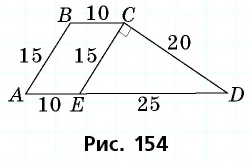
Основания трапеции равны 10 см и 35 см, а боковые стороны — 15 см и 20 см. Найдите площадь трапеции.

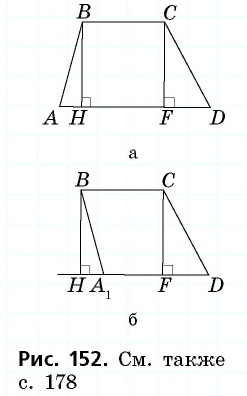
Прежде всего заметим, что решение данной задачи фактически сводится к нахождению высоты трапеции. Итак, пусть дана трапеция

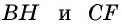
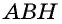
Естественно было бы провести, как в предыдущей задаче, высоты (рис. 153) и составить уравнение на основании теоремы Пифагора, примененной к треугольникам и

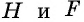
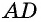
Такое решение позволит получить правильный ответ, но не будет полным, ведь принадлежность точек отрезку нужно обосновать. Попробуем избежать необходимости такого обоснования, применив для решения другое дополнительное построение.

Решение:

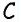
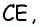
Проведем через вершину прямую параллельную (рис. 154).

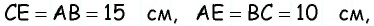
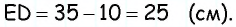
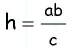
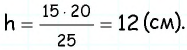
Поскольку по построению — параллелограмм, то следовательно, Стороны треугольника пропорциональны числам 3, 4, 5, следовательно, по теореме, обратной теореме Пифагора, он является прямоугольным с гипотенузой

По формуле находим высоту этого треугольника, которая одновременно является и высотой трапеции: Следовательно,

Ответ: 270

Как видим, этот способ намного более рационален, в частности, с точки зрения вычислений. Рассмотрим еще одну задачу, для решения которой используется дополнительное построение.

Пример:

Диагонали трапеции равны 30 см и 40 см и пересекаются под прямым углом. Найдите площадь трапеции.

Попробуем решить эту задачу чисто геометрическими методами. Основная сложность заключается в том, что данные отрезки не являются сторонами одного треугольника. Попробуем «исправить» эту ситуацию.

Решение:

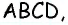
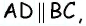
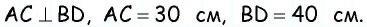
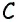
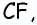
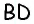
Пусть дана трапеция в которой Проведем через вершину прямую параллельную диагонали (рис. 155).

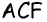
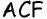
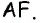
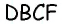
Очевидно, что по построению угол будет прямым, т.е. треугольник прямоугольный с гипотенузой С другой стороны, — параллелограмм, тогда

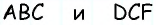
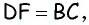
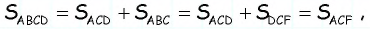
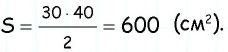
Обратим внимание на то, что треугольники равновеликие, поскольку а высоты, проведенные к этим сторонам, являются высотами трапеции. Таким образом, т.е. искомая площадь трапеции равна площади треугольника которая, в свою очередь, равна полупроизведению его катетов:

Ответ: 600

Применение площадей

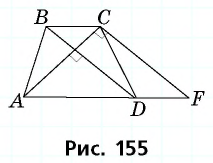
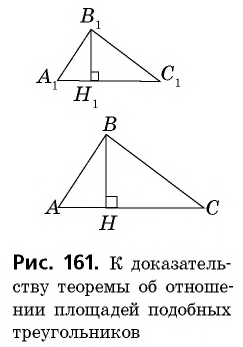
Теорема (об отношении площадей подобных треугольников)

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

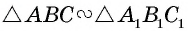
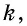
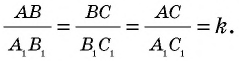
Пусть с коэффициентом т.е. Докажем, что

Проведем в данных треугольниках высоты 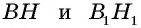(рис. 161).

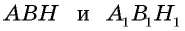
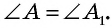
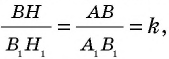
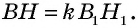
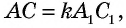
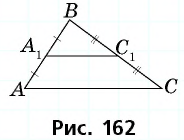
Прямоугольные треугольники подобны, поскольку Это означает, что т.е. Учитывая, что имеем:

Пример:

Средняя линия отсекает от данного треугольника треугольник с площадью 8 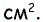Найдите площадь данного треугольника.

Решение:

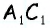
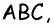
Пусть — средняя линия треугольника параллельная стороне (рис. 162),

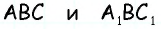
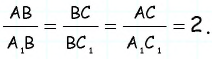
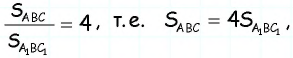
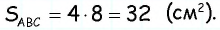
Треугольники подобны по двум сторонам и углу между ними, причем Тогда по доказанной теореме откуда
Ответ:

Метод площадей

Понятия площади и формулы ее вычисления могут применяться даже в тех задачах, в условиях которых площадь не упоминается. Рассмотрим такой пример.

Пример:

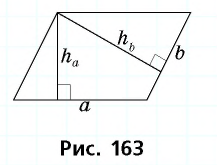
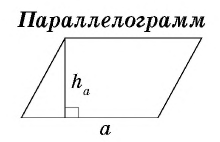
Стороны параллелограмма равны 16 см и 12 см. Высота параллелограмма, проведенная к большей стороне, равна 3 см. Найдите высоту, проведенную к меньшей стороне.

Решение:

Пусть дан параллелограмм со сторонами 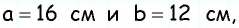к которым проведены высоты длину которой необходимо найти (рис. 163).

По формуле площади параллелограмма 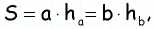откуда

Таким образом,

При решении этой задачи площадь параллелограмма вычислялась двумя разными способами. Поскольку площадь многоугольника независимо от способа ее вычисления определяется однозначно, то полученные выражения приравнивались, благодаря чему удалось связать известные величины с искомой. Такой метод, основанный на использовании площади как вспомогательной величины, называется методом вспомогательной площади или просто методом площадей.

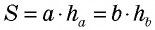
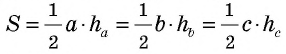
Заметим, что из формул площади параллелограмма и площади треугольника следует важное утверждение: в параллелограмме (треугольнике) большей является высота, проведенная к меньшей стороне, меньшей — высота, проведенная к большей стороне.

Метод площадей используется как в задачах на вычисление, так и для доказательства утверждений.

Пример:

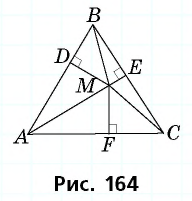
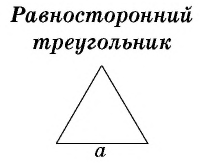
Сумма расстояний от точки, взятой внутри равностороннего треугольника, до его сторон не зависит от выбора точки и равна высоте треугольника. Докажите.

Решение:

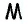
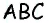
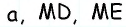
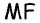
Пусть точка лежит внутри равностороннего треугольника со стороной и — расстояния от данной точки до сторон треугольника (рис. 164).

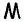
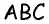
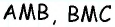
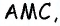
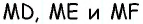
Соединим точку с вершинами треугольника. Площадь треугольника равна сумме площадей треугольников и в которых отрезки являются высотами. Имеем:

Отсюда 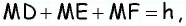т.е. сумма рассматриваемых расстояний равна высоте треугольника и не зависит от выбора точки

Другие доказательства теоремы Пифагора

Исторически появление и доказательство теоремы Пифагора связаны с вычислением площадей. Поэтому в классической формулировке этой теоремы речь идет не о квадратах сторон прямоугольного треугольника, а о площадях соответствующих фигур:

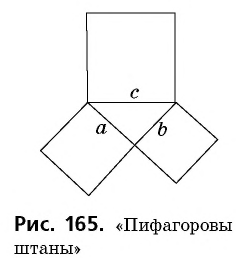
• площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.

Рисунок 165, который наглядно воплощает эту формулировку, стал своеобразным символом геометрии и среди гимназистов позапрошлого столетия получил название «пифагоровы штаны».

Шутливый стишок про «пифагоровы штаны» школьники запоминали на всю жизнь.

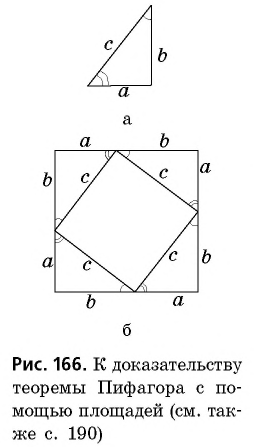
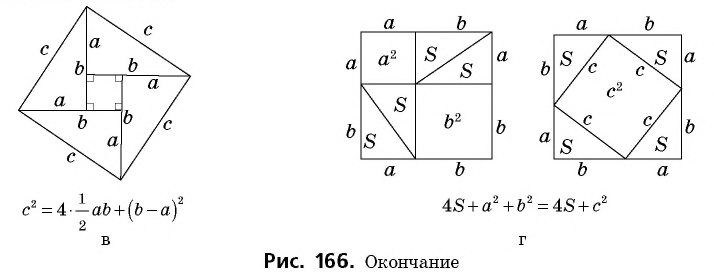
Докажем теорему Пифагора с помощью площадей.

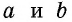
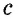
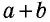
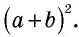
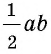
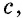
Пусть дан прямоугольный треугольник с катетами и гипотенузой (рис. 166, а). Достроим его до квадрата со стороной так, как показано на рисунке 166, б. Площадь этого квадрата равна Построенный квадрат состоит из четырех равных прямоугольных треугольников площадью и четырехугольника со сторонами длиной который является квадратом (докажите это самостоятельно). Итак, имеем: ^

т.е.

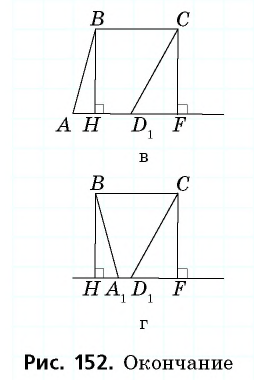
На рисунках 166, в, г показаны другие способы доказательства теоремы Пифагора с помощью площадей. В трактатах индийского математика XII ст. Бхаскари один из них сопровождался только одним словом: «Смотри!». В целом сегодня известно более 150 разных способов доказательства этой знаменитой теоремы. Но каждый из вас может изобрести и свой собственный способ.

Многоугольник называется выпуклым, если он лежит по одну сторону от любой прямой, содержащей его сторону

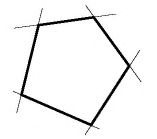
Сумма углов многоугольника
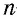
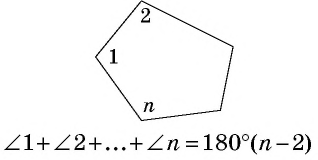
Сумма углов выпуклого -угольника равна

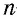
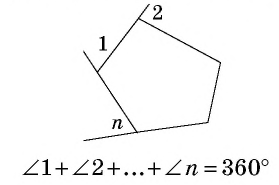
Сумма внешних углов выпуклого -угольника, взятых по одному при каждой вершине, равна

Описанный многоугольник

Многоугольник называется вписанным в окружность, если все его вершины лежат в этой окружности.

Описанный многоугольник.

Многоугольником называют описанным около окружностей, если все его стороны касаются этой окружности.

Аксиомы площадей

1. Равные многоугольники имеют равные площади.
2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
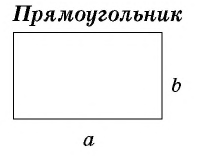
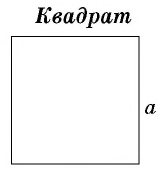
3. Площадь квадрата со стороной, равной единице длины, равна единице площади

Две фигуры называются равновеликими, если они имеют равные площади

где — стороны прямоугольника.

где — сторона квадрата

где — сторона параллелограмма,

— проведенная к ней высота

где — сторона треугольника, — проведенная к ней высота.

— катеты прямоугольного треугольника.

где — сторона треугольника.

где — диагонали ромба.

где основание трапеции, — высота трапеции.

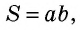
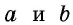
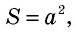
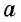
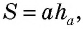
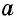
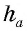
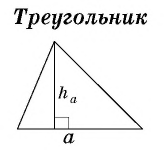
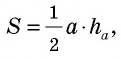
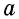
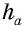
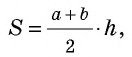
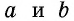
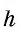
Теорема об отношении площадей подобных треугольников Отношение площадей подобных треугольников равно квадрату коэффициента подобия

Историческая справка:

Вычисление площадей многоугольников — первая среди тех практических задач, благодаря которым появилась геометрия как наука. Но не всегда представление об измерении площадей было таким, как сегодня.

Например, древние египтяне при вычислении площади любого треугольника брали половину произведения двух его сторон. Так же пять столетий назад измеряли площадь треугольника и в Древней Руси. Чтобы найти площадь четырехугольника, который не является квадратом, в Вавилоне использовали формулу произведения полусумм его противолежащих сторон.

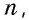
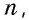
В Средние века для вычисления площади треугольника со стороной и проведенной к ней высотой, которые выражаются целым числом брали сумму членов натурального ряда от 1 до т.е. число

Кстати, в то время знали и правильную формулу площади этого треугольника 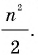Ее обосновал средневековый математик Герберт, который в X ст. даже занимал какое-то время престол Римского Папы под именем Сильвестра II.

Древние вавилоняне еще четыре тысячи лет назад умели правильно вычислять площадь квадрата, прямоугольника, трапеции. Немало формул площадей и объемов, с которыми вы познакомитесь в старших классах, открыл знаменитый греческий ученый Архимед (ок. 287-212 гг. до н. э.). И это все при том, что в те древние времена не было даже алгебраической символики!

Сегодня, благодаря значительно более широкому применению алгебры в геометрии, мы имеем возможность дать куда более простые и понятные решения многих задач, чем это было возможно в те далекие времена.

• Тела вращения: цилиндр, конус, шар
• Четырехугольник
• Площади фигур в геометрии
• Площади поверхностей геометрических тел
• Эллипс
• Гипербола
• Парабола
• Многогранник

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.