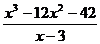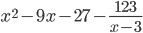Делить уравнение на уравнение в системе

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Деление многочлена на многочлен (двучлен) столбиком (уголком)

С помощью данной математической программы вы можете поделить многочлены столбиком.
Программа деления многочлена на многочлен не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вам нужно или упростить многочлен или умножить многочлены, то для этого у нас есть отдельная программа Упрощение (умножение) многочлена

Немного теории.

Деление многочлена на многочлен (двучлен) столбиком (уголком)

В алгебре деление многочленов столбиком (уголком) — алгоритм деления многочлена f(x) на многочлен (двучлен) g(x), степень которого меньше или равна степени многочлена f(x).

Алгоритм деления многочлена на многочлен представляет собой обобщенную форму деления чисел столбиком, легко реализуемую вручную.

Для любых многочленов $ f(x) $ и $ g(x) $, $ g(x) \neq 0 $, существуют единственные полиномы $ q(x) $ и $ r(x) $, такие что
$$ \frac = q(x)+\frac $$
причем $ r(x) $ имеет более низкую степень, чем $ g(x) $.

Целью алгоритма деления многочленов в столбик (уголком) является нахождение частного $ q(x) $ и остатка $ r(x) $ для заданных делимого $ f(x) $ и ненулевого делителя $ g(x) $

Пример

Разделим один многочлен на другой многочлен (двучлен) столбиком (уголком):
$$ \frac $$

Частное и остаток от деления данных многочленов могут быть найдены в ходе выполнения следующих шагов:
1. Делим первый элемент делимого на старший элемент делителя, помещаем результат под чертой $ (x^3/x = x^2) $

$ x^3 $

$ -12x^2 $

$ +0x $

$ -42 $

$ x $	$ -3 $
$ x^2 $

2. Умножаем делитель на полученный выше результат деления (на первый элемент частного). Записываем результат под первыми двумя элементами делимого $ (x^2 \cdot (x-3) = x^3-3x^2) $

$ x^3 $	$ -12x^2 $	$ +0x $	$ -42 $
$ x^3 $	$ -3x^2 $

$ x $	$ -3 $
$ x^2 $

3. Вычитаем полученный после умножения многочлен из делимого, записываем результат под чертой $ (x^3-12x^2+0x-42-(x^3-3x^2)=-9x^2+0x-42) $

$ x^3 $	$ -12x^2 $	$ +0x $	$ -42 $
$ x^3 $	$ -3x^2 $
$ -9x^2 $	$ +0x $	$ -42 $

$ x $	$ -3 $
$ x^2 $

4. Повторяем предыдущие 3 шага, используя в качестве делимого многочлен, записанный под чертой.

$ x^3 $	$ -12x^2 $	$ +0x $	$ -42 $
$ x^3 $	$ -3x^2 $
$ -9x^2 $	$ +0x $	$ -42 $
$ -9x^2 $	$ +27x $
$ -27x $	$ -42 $

$ x $	$ -3 $
$ x^2 $	$ -9x $

5. Повторяем шаг 4.

$ x^3 $	$ -12x^2 $	$ +0x $	$ -42 $
$ x^3 $	$ -3x^2 $
$ -9x^2 $	$ +0x $	$ -42 $
$ -9x^2 $	$ +27x $
$ -27x $	$ -42 $
$ -27x $	$ +81 $
$ -123 $

$ x $	$ -3 $
$ x^2 $	$ -9x $	$ -27 $

6. Конец алгоритма.
Таким образом, многочлен $ q(x)=x^2-9x-27 $ — частное деления многочленов, а $ r(x)=-123 $ — остаток от деления многочленов.

Результат деления многочленов можно записать в виде двух равенств:
$ x^3-12x^2-42 = (x-3)(x^2-9x-27)-123 $
или
$$ \frac = x^2-9x-27 + \frac<-123> $$

Деление многочленов столбиком

Алгоритм деления в столбик применяется в частности при нахождении интегралов.

Решение онлайн
Видеоинструкция

Пример деления в столбик . Найти частное деления и остаток многочлена:

№1.

x 3 -12x 2 -42	x -3
x 3 -3x 2	x 2
-9x 2 -42

№2.

x 3 -12x 2 -42	x -3
x 3 -3x 2	x 2 -9x
-9x 2 -42
-9x 2 + 27x
-27x -42

№3.

x 3 -12x 2 -42	x -3
x 3 -3x 2	x 2 -9x -27
-9x 2 -42
-9x 2 + 27x
-27x -42
-27x + 81
-123

Целая часть: x 2 -9x -27
Остаток: -123

Таким образом, ответ можно записать как:
см. также и другие примеры решение столбиком.

Пример №1 . Найти частное и остаток от деления многочлена на многочлен:
P(x)=2x 5 +3x 3 -x 2 +4x+1, Q(x)=2x 2 -x+1

Пример №2 . Не производя деление найти остаток от деления многочлена на двучлен:
P(x)=-x 4 +6x 3 -2x 2 +x-2, Q(x)=x-6
Решение. Выделим общий множитель (x-6).
-x 3 (x-6)-2x(x-6)-12x+x-2 = -x 3 (x-6)-2x(x-6)-11(x-6)-66-2 = -x 3 (x-6)-2x(x-6)-11(x-6)-68
Остаток от деления: -68/(x-6)

Системы алгебраических уравнений

Систему уравнений можно решать методом подстановки – выражать переменную из одного уравнения и подставлять в другое.

Уравнения в системе можно также складывать друг с другом и вычитать одно из другого. Например, левую часть одного уравнения складываем с левой частью другого, правую – с правой.

Можно умножать и даже делить одно уравнение на другое! Конечно, при этом надо следить, чтобы не умножить или не поделить на ноль.

Обратите внимание – когда мы решаем систему уравнений, она не распадается на «кусочки», на отдельные уравнения. Каждый раз мы переходим от системы уравнений к равносильной ей системе.

1. Решите систему уравнений:

Раскроем скобки в каждом уравнении:

Вычтем из первого уравнения системы второе: . И подставим во второе уравнение.

2. Решите систему уравнений:

Мы разложили левую часть первого уравнения на множители по формуле суммы кубов.

Поделим первое уравнение системы на второе

Подставим в уравнение

3. Решите систему уравнений:

Дальше – цепочка равносильных переходов.

Решения первой системы:

Решим квадратное уравнение . Его корни:
и .

Это полезно

Узнаете, чем отличаются официально-деловой, публицистический, научный, художественный и разговорный стили.

источники:

http://math.semestr.ru/gauss/factor.php

http://ege-study.ru/sistemy-algebraicheskix-uravnenij/