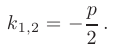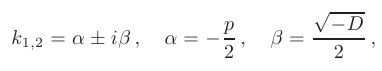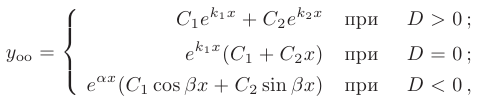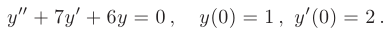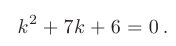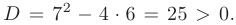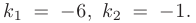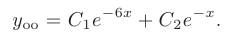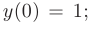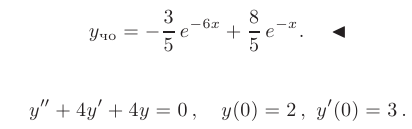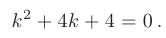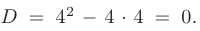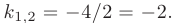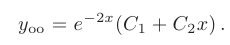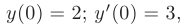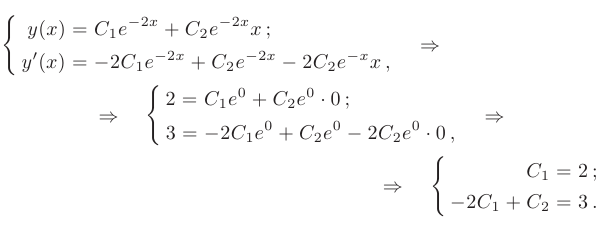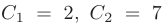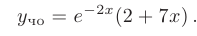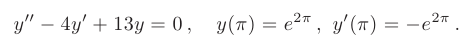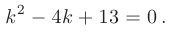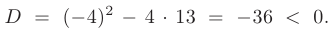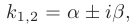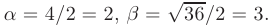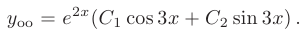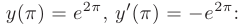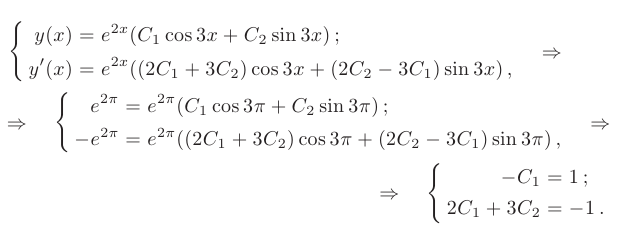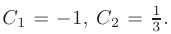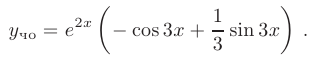Линейные однородные дифференциальные уравнения с постоянными коэффициентами
Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
Частный случай: уравнение второго порядка Пусть имеем линейное однородное дифференциальное уравнение второго порядка где р\, Р2 — действительные числа. Чтобы найти общее решение этого уравнения, надо найти два его линейно независимых частных решения. Следуя Эйлеру, будем искать их в виде где тогда Подставляя эти выражения для у и ее производных в уравнение (1), получаем .
Так как , то должно выполняться равенство Следовательно, функция у = eAz будет решением уравнения (1), т. е. будет обращать его в тождество по х, если А будет удовлетворять алгебраическому уравнению Уравнение (3) называется характеристическим уравнением по отношению к уравнению (1), а его левая часть называется характеристическим много-членом.
Уравнение (3) есть квадратное уравнение. Обозначим его корни через А] и 1 они могут быть 1) действительными и разными; 2) комплексными; 3) действительными и равными. Рассмотрим каждый случай в отдельности. 1. Если корни Л|, Аг характеристического уравнения действительные и разные, то частными решениями уравнения (1) будут функции Эти решения линейно независимы (Aj Ф А2) и, следовательно, образуют фундаментальную систему решений уравнения.
Общее решение уравнения
Общее решение уравнения имеет вид — произвольные постоянные). Пример 1. Найти общее решение уравнения М Составляем характеристическое уравнение: Оно имеет корни Линейные однородные дифференциальные уравнения с постоянными коэффициентами Общий случай: уравнение произвольного порядка Физические приложения: уравнение колебаний Уравнения, приводящие к уравнениям с постоянными коэффициентами Линейные неоднородные дифференциальные уравнения Отсюда получаем искомое общее решение 2.
Пусть корни характеристического уравнения комплексные. Так как коэффициенты р], р2 характеристического уравнения действительные, комплексные корни входят попарно сопряженными. Положим, что Частные решения дифференциального уравнения (1) можно записать в виде Это комплекснозначные функции действительного аргумента х, а мы будем заниматься лишь действительными решениями.
С помощью формул Эйлера частные решения ij\ и у2 уравнения (1) можно представить в виде Воспользовавшисьтеоремой 4, получим, что частными решениями уравнения (1) будут также функции _ Эти решения линейно независимы, так как Решения образуют фундаментальную систему решений уравне-ния (1), общее решение которого в этом случае имеет вид или Пример 3.
Найти общее решение уравнения 4 Характеристическое уравнение имеет кратные корни Поэтому общее решение исходного дифференциального уравнения: Замечание. Пусть имеем линейное однородное дифференциальное уравнение (вообще, с переменными коэффициентами) Пусть — частное решение уравнения. Введем новую искомую функцию ti(x) соотношением (разрешимым относительно н(х) в тех интервалах, где yi(x) не обращается в нуль).
Из этого соотношения найдем производные от у : и подставим их в уравнение (5): Для функции и(х) получаем опять уравнение порядка п, но коэффициент при м(х) есть £(yil-Он тождественно равен нулю, так как yi (х) есть решение уравнения (5). Следовательно, в полученном уравнении порядок понизится, если ввести новую искомую функцию z(x) = и'(х).
Разделив, кроме того, все члены последнего уравнения на yi(x) Ф 0, приведем его к виду Итак, если известно частное решение уравнения (5), то задача интегрирования этого уравнения приводится к интегрированию линейного однородного уравнения порядка п — \. Можно показать, что если известны два частных линейно независимых решения, то порядок уравнения может быть понижен на две единицы. Вообше, если известно г частных линейно независимых решений линейного однородного дифференциального уравнения, то порядок этого уравнения может быть понижен на г единиц. 6.2.
Физические приложения: уравнение колебаний Линейные дифференциальные уравнения с постоянными коэффициентами возникают в задачах о механических и электрических колебаниях. Рассмотрим уравнение свободных механических колебаний, причем независимой переменной будем считать время t: где у — отклонение колеблющейся точки от положения равновесия, rh — масса точки, h — коэффициент трения (считаем, что сила трения пропорциональна скорости), к > 0 — коэффициент упругости восстанавливающей силы (считаем, что эта сила пропорциональна отклонению).
Характеристическое уравнение
Характеристическое уравнение для (6) имеет корни Если трение достаточно велико, h2 > Атк, то эти корни действительные и отрицательные. Общее решение уравнения (6) в этом случае имеет вид Так как то из (7) заключаем, что при большом трен и и отклонение точки от положения равновесия с возрастанием t стремится к нулю, не совершая колебаний. Если трение мало, Атк, то характеристическое уравнение имеет комплексно сопряженные корни Общее решение уравнения (6) в этом случае определяется формулой или Отсюда видно, что в случае малого трения происходят затухающие колебания. Пусть теперь трение отсутствует, .
В этом случае характеристическое уравнение имеет чисто мнимые корни Решение уравне- ния (6) имеет вид . в этом случае происходят незатухающие гармонические колебания с частотой ш = и произвольными амплитудой А и начальной фазой 6. Задача. При каких 1) все решения уравнения стремятся к нулю при 2) каждое решение уравнения обращается в нуль на бесконечном множестве точек х? 6.3. Общий случай: уравнение произвольного порядка Рассмотрим теперь линейное однородное дифференциальное уравнение произвольного порядка п (п ^ 1) с постоянными коэффициентами ) гдерьрг,,Рп — действительные числа.
Общее решение дифференциального уравнения (8) находим так же, как и в случае уравнения второго порядка. Ищем решение в виде Подставляя вместо у величину еХх в уравнение (8), получаем , что приводит к характеристическому уравнению 2. Находим корни характеристического уравнения. 3. По характеру корней выписываем частные линейно независимые решения уравнения (8), руководствуясь тем, что: а) Каждому действительному однократному корню А характеристическою уравнения соответствует частное решение уравнения (8).
б) Каждой паре однократных комплексно сопряженных корней соответствуют два линейно независимых частных решения уравнения (8). в) Каждому действительному корню А кратности г соответствует г линейно независимых частных решений уравнения (8). Рассмотрим случай в) подробнее. Пусть число А есть корень кратности г характеристического уравнения . Функцию будем рассматривать как функцию двух аргументов: ж и А.
Возможно вам будут полезны данные страницы:
Она имеет непрерывные производные по а: и по А всех порядков, причем Поэтому частные производные функции по х и по А не зависят от порядка дифференцирования (операции дифференцирования функции у по х и по А перестановочны), так что Воспользовавшись этой перестановочностью, а также тем, что Если А есть г-кратный корень характеристического уравнения то стало быть, правые части (10) и (11) тождественно по х равны нулю: Это означает, что функции являются в этом случае решениями уравнения (8).
Легко проверить, что функции линейно независимы на любом интервале (a, b) изменения х. г) Приведенные в пункте в) рассуждения сохраняют силу и для комплексных корней.
Поэтому каждой паре комплексно сопряженных корней p кратности \l отвечает 2/х частных решений уравнения 4. Число построенных таким образом частных решений уравнения (8) равно порядку п этого уравнения. Можно показать, что все эти решения линейно независимы в совокупности. Имея п линейно независимых частных решений 3/i(x), skfc). уп(я) уравнения (8), получаем общее решение этого уравнения, где произвольные постоянные. Прммер 4. Найти общее решение уравнения Составляем характеристическое уравнение: 2. Находим корни характеристического уравнения: 3.
По характеру корней выписываем частные линейно независимые решения дифференциального уравнения: 4. Общее решение дифференциального уравнения имеет вид Схема решения линейного дифференциального уравнения с постоянными коэффициентами Дифференциальное уравнение действительные числа). Характеристическое уравнение Корни характеристического уравнения Частные линейно независимые решения дифференциального уравнения Общее решение уравнения — произвольные постоянные). §7.
Уравнения, приводящие к уравнениям с постоянными коэффициентами Существуют линейные дифференциальные уравнения с переменными коэффициентами, которые с помощью замены переменных преобразуются в уравнения с постоянными коэффициентами. К их числу принадлежит уравнение Эйлера где pi.tp2, —tPn — постоянные числа.
Ограничимся рассмотрением уравнения Эйлера 2-го порядка (оно встречается в задачах математической физики): Линейные однородные дифференциальные уравнения с постоянными коэффициентами Общий случай: уравнение произвольного порядка Физические приложения: уравнение колебаний Уравнения, приводящие к уравнениям с постоянными коэффициентами Линейные неоднородные дифференциальные уравнения Положим Подставляя выражения для , получим дифференциальное уравнение с постоянными коэффициентами.
Последнее интегрируется обычным приемом: составляем характеристическое уравнение находим его корни и по характеру корней выписываем общее решение уравнения (2), после чего возвращаемся к старой переменной х. Пример. Найти общее решение уравнения Замена переменной х = приводит к уравнению характеристическое уравнение которого имеет корни Общее решение преобразованного уравнения равно Учитывая, что , для общего решения исходного уравнения получаем выражение Замечание 1.
Для преобразованного уравнения (2) в случае действительных и различных корней характеристического уравнения (3) частные решения имеют вид Поэтому можно сразу задаться этим видом частного решения. Подставляя в уравнение (1), получим для к уравнение ) совпадающее с (3). Каждому простому действительному корню уравнения (4) отвечает частное решение уравнения (1); двукратному корню отвечают два решения уравнения (1).
Паре комплексных сопряженных корней уравнения (4) будут соответствовать два решения уравнения (I). Замечание 2. Уравнение постоянные числа) подстановкой также приводится к уравнению с постоянными коэффициентами. §8. Линейные неоднородные дифференциальные уравнения Линейное неоднородное дифференциальное уравнение п-го порядка имеет вид Здесь заданные на некотором интервале (а, р) функции. Если ао(ж) Ф 0 на (а, то после деления на ац(х) получим уравнение.
Из теоремы 1 существования и единственности решения задачи Коши получаем: если на отрезке [а, 6] коэффициенты Рк(х) и правая часть /(х) уравнения (2) непрерывны, то это уравнение имеет единственное решение, удовлетворяющее условиям Уравнение (2) можно записать в виде где, как и выше, Теорема 12. Если у(х) есть решение неоднородного уравнения есть решение соответствующего однородного уравнения мПо условию, В силу линейности оператора £ имеем Это означает, что функция есть решение уравнения Теорема 13.
Если у\(х) есть решение уравнения есть решение уравнения та функция есть решение уравнения По условию, используя линейность оператора £, получаем Последнее означает, что функция есть решение уравнения Теорема выражает так называемый принцип суперпозиции (наложения). Теорема 14. Если уравнение где все коэффициенты и функции действительные, имеет решение то действительная часть решения и(х) и его мнимая часть v(x) являются соответственно решениями уравнений.
По условию имеем Отсюда получаем: Теорема 15 (о структуре общего решения линейного неоднородного дифференциального уравнения). Общее решение в области — уравнения с непрерывными на отрезке коэффициентами , и правой частью f(x) равно сумме общего решения соответствующего однородного уравнения и какого-нибудь частного решения у(х) неоднородного уравнения, т. е. Надо доказать, что где произвольные постоянные, линейно независимые решения соответствующего однородного уравнения £[у] = 0, является общим решением неоднородного уравнения.
Будем исходить из определения общего решения и просто проверим, что семейство функций у(ж), определяемое формулой (4), удовлетворяет условиям 1) и 2), содержащимся в этом определении. В самом деле, функция у(х), определяемая формулой (4), является решением уравнения (2) при любых значениях постоянных, поскольку сумма какого-либо решения неоднородного уравнения и любого решения соответствующего однородного уравнения есть решение неоднородного уравнения.
Так как для уравнения (2) при х 6 [а, Ь] выполнены условия теоремы 1 существования и единственности решения задачи Коши, то остается показать, что подбором постоянных С\, в (4) можно удовлетворить произвольно заданным начальным условиям где хо € (а,6), т.е. можно решить любую задачу Коши. Ограничимся случаем, когда п = 3.
Потребовав, чтобы решение (4) удовлетворяло начальным условиям (5), приходим к системе уравнений для отыскания Эта линейная по отношению к система трех уравнений с тремя неизвестными допускает единственное решение относительно з при произвольных правых частях, так как определитель этой системы есть определитель Вронского W(x$) для линейно независимой системы решений соответствующего однородного уравнения и, следовательно, отличен от нуля в любой точке ж € (а, Ь), в частности в точке ж = жо.
| Значит, какова бы ни была тройка чисел |
уо, Уо> Уо» найдется решение С?, С?, Cj системы (6) такое, что функция будет решением дифференциального уравнения (2), удовлетворяющим начальным условиям Линейные однородные дифференциальные уравнения с постоянными коэффициентами Общий случай: уравнение произвольного порядка Физические приложения: уравнение колебаний.
Уравнения, приводящие к уравнениям с постоянными коэффициентами Линейные неоднородные дифференциальные уравнения Из этой теоремы следует, что задача нахождения общего решения линейного неоднородного уравнения сводится к отысканию какого-либо частного решения этого неоднородного уравнения и общего решения соответствующего однородного уравнения. Интегрирование линейного неоднородного дифференциального уравнения методом вариации постоянных 155 Пример 1.
Найти общее решение уравнения М Нетрудно заметить, что функция является частным решением данного неоднородного уравнения. Чтобы найти общее решение этого уравнения, остается отыскать общее решение соответствующего однородного уравнения Это уравнение есть линейное однородное уравнение с постоянными коэффициентами. Характеристическое уравнение, соответствующее уравнению , есть корни его Поэтому общее решение уравнения (*) имеет вид . Общее решение исходного неоднородного уравнения:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Простейшие типы точек покоя
Пусть имеем систему двух линейных однородных дифференциальных уравнений с постоянными коэффициентами причем
Точка , в которой правые части уравнений системы (1) обращаются в ноль, называется точкой покоя системы (1).
Для исследования точки покоя системы (1) надо составить характеристическое уравнение
и найти его корни и .
Возможны следующие случаи.
1. Корни характеристического уравнения (2) вещественные и разные:
а) . Точка покоя асимптотически устойчива (устойчивый узел, рис. 32);
б) 0,\,\lambda_2>0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAH4AAAATCAMAAABhl0k+AAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAMWHQwCEQA0GageBx8LFRDpCt4AAAAbhJREFUSMfFVldyxCAMpUei6v6nDQZcFsvZkMwk/vDs2KxeUbMQ/34p493KeQnMQzRlJYYDefyOhAvgOmNQ9+eG5ILigKiP8yl8/5/BVwp0N6AsaICNqg+750isc8i4rMhuUs39Da8BuMRmXW+Wdg8ly/zDorkRyNTvt6AfDxqUQTs/o8ae8uFoYk2qBPSUZt3gPeO+fHIfZgIw4A+7kJR4IOBfCdAj/JOGRuDFRiB/hup1M4xgqtd5fcnfDs/QHRosMNTkNY8zvAyhJdNnYps0av9evdJNA2DJxn1ZSNDTtMPLVCLFRpz4Nj3hwxO80k5vGkwULsV7jFpGZcp9GuiqdoHuL96Zb6jf52qOSYqmwSDXl/Y6Fd2ANx0dWytZFr6Cq6uVsff9VrSXuVnzLsWuoYaf1MPUwbr3fWzouY8TZODvjeeSHxND0mnBqLquQXg9Nx4wsysm25i4c2i9wltuj1SzlN6o2nAUgByN0GtK4dWuwowdgSGOxWHHWQtuhs/A9oGKw3V/vN/TIOXWY1XZxXfLBbGxOG4XrGzNzO1paQCK/9HmN5rMwt5ijwaql/qDzxR0vw7xCYY/D3jyG++NAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />. Точка покоя неустойчива (неустойчивый узел, рис. 33);
в) 0,\,\lambda_2 . Точка покоя неустойчива (седло, рис. 34).
2. Корни характеристического уравнения (2) комплексные:
а) . Точка покоя асимптотически устойчива (устойчивый фокус, рис.35);
q\ne0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAGoAAAAVCAMAAACZi4uxAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAYSHAEJnpQYEB0DHBcbFSUNy43AAAAbpJREFUSMfVVcmShCAMFQKBsJn//9phUTvYdpfW1ByGg5ZWyPMtxGX570v/arN7sF0X+RQdPUGy6JM1d6uLE0BoLaonSBUm2ZvVTpAy6Cscu6s6r97p9vpF8U0NQdRlblqEclVnfMhnpVbO7WP5ng5Osk9MxzVCMdGC6GJU8DOY7wI49m9tFZTo8vwuCVKEG1RrEAwGawzKelLB6guodFYAQt3JeU9aXwraddtO/IKqbBGbvmGyaAazH6B6WizHTWbfF/ZrnKB6Axdj12UQlWAuHWAfWEVurgDSR6d2KBgRzO1mGJczVLXhBHVKu+W1NZvSRUlfQA2vltIe1lObCiQEVFsC51gQtCC73aohoB367QJu2euVNSPQ8FB/iYXmca7qfi2iCtgZx0XEAtcRDn0w7+cqDMHxdGSoh51m/1vn9k2Bswgm1bkzWaXO50G3aOvRPrMFi04eYf827EwqqoT6miwm8RZKmayi8LZVoc043KlWaU1yMF1OVefH15CRrY1xnL+R6hMh6+04w7O/iZpnQz6suiY1jTf76G9iYOpmApvvpMTAAiiPSK0TJ0gJXj4Hs/zlIrr5n/8Bj3oQCknmmsUAAAAASUVORK5CYII=» style=»vertical-align: middle;» />. Точка покоя неустойчива (неустойчивый фокус, рис.36);
q\ne0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAGoAAAAVCAMAAACZi4uxAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAYSHAEJnpQYEB0DHBcbFSUNy43AAAAbpJREFUSMfVVcmShCAMFQKBsJn//9phUTvYdpfW1ByGg5ZWyPMtxGX570v/arN7sF0X+RQdPUGy6JM1d6uLE0BoLaonSBUm2ZvVTpAy6Cscu6s6r97p9vpF8U0NQdRlblqEclVnfMhnpVbO7WP5ng5Osk9MxzVCMdGC6GJU8DOY7wI49m9tFZTo8vwuCVKEG1RrEAwGawzKelLB6guodFYAQt3JeU9aXwraddtO/IKqbBGbvmGyaAazH6B6WizHTWbfF/ZrnKB6Axdj12UQlWAuHWAfWEVurgDSR6d2KBgRzO1mGJczVLXhBHVKu+W1NZvSRUlfQA2vltIe1lObCiQEVFsC51gQtCC73aohoB367QJu2euVNSPQ8FB/iYXmca7qfi2iCtgZx0XEAtcRDn0w7+cqDMHxdGSoh51m/1vn9k2Bswgm1bkzWaXO50G3aOvRPrMFi04eYf827EwqqoT6miwm8RZKmayi8LZVoc043KlWaU1yMF1OVefH15CRrY1xnL+R6hMh6+04w7O/iZpnQz6suiY1jTf76G9iYOpmApvvpMTAAiiPSK0TJ0gJXj4Hs/zlIrr5n/8Bj3oQCknmmsUAAAAASUVORK5CYII=» style=»vertical-align: middle;» />. Точка покоя устойчива (центр, рис. 37).
3. Корни кратные:
а) . Точка покоя асимптотически устойчива (устойчивый узел, рис.38, 39);
б) 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAGgAAAATBAMAAACO11WQAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQoFewKTnMRAg0CJxkY7DLSgAAAFdSURBVCjPY2AgC/D4YBc/cgC7uDiYjDPAKsn6GKtwWWg6iJoXgFWW8xU2Ue5kBrMNQJrrJXZ3+G2AM6dOgLF4HzDwXQDSzG+wa7JDeIrRtQDKYnNgYFkApDleYdfUl4BgM4YIQBh8QE0PwCEBM4aBXRAMGiAh8RzZLyGQ4NoH02QHdCQnWIhZCQwghjC/ZWBolIDrCgPrkgNqeggyPi2BYdISLIGbxsAZGAYPAg4tAyRNZqWPGTpVMPSwp8cZ8AZwBaBqgvqJ+SHjUwYGFQzn2RnUBfAu4IWFBjdYDyj0uBJAkgxpDVBNSAHB/JiB7QUwEqE2cUdBAoIVGE8BYO/qGTBgOM8ugIEJmJCsGqCBBw1yxocMcgIgfQzzHDA1AZ3MmcLA7gFR6iIAEzc7kwx0EcgcAUxNIH9tZGhpACeLUkSK4jaGhyemJkiIOQoG4M5UJWnOWLPHu3cXGKgEAGUFSl2PiR1zAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />. Точка покоя неустойчива (неустойчивый узел, рис.40, 41).
Пример 1. Определить характер точки покоя (0,0) системы
Решение. Составляем характеристическое уравнение
\lambda_2=3-\sqrt<2>>0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAS8AAAAXBAMAAACortSfAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQRGBpGbAgugg0DGRUU3Z2TAAAAPiSURBVEjH7VbdS5NRGH/ed3v30TZZZUE3Mk3Muoih4IUXMi3NLRhvRmQFY2mJGogYfdCFSKVMLFmgoRAiYiB9yAITMYgFEeWF6EW34nTm1Lm/ofPxfu19T2qw7nou9Ow55/zO7/yej/cA/Ld/badHkXlyBofRRnMBxA9mkHXmipcZo6VygWRqKEKWM8VeYrQi9tz5JbY0J5humwdeGJycWyXezD5Fs0Rr1cAfMTg/0HuXrjG31D18y3Jfhfn2pE4w17Pv6rGLImub8K6e5bePw0KH/pyS5id0zwYLydnEp+j5XFTrn+DvQCicvXZkSehXfoyFWXBzMcsuw20VnaIjEs123oJScgn7NgvJsgEdVAarNghCJ5cEWwKNHD8UZxAgrW7cYsF1h01phvsM2PphMY6rQDnFsQvmHoobZWnfBpmYkdghj5AC8zoeHvfLzj6AVnUjMwCzopPlvwd5O1CANbbXyaG2JsC0Q0YhLztdf0np7M5KMbiB1cSWf1NyooUdatFss7O/9DGjwMaBE2GFBJ9/JDGzrIGVhv1sj7LyMDHChGusYRBr0p4xRJk5MDG1HoIxJSgUjgRk+E2MlWJkA2XEV5ZRYqtg3aThQcLxNJwPiJEFpgp/NjG8hPPhUZWs+lCvLG2Hyj4UB36Z8HRROMLoaEDXlewkxTD9pKzf9TKJmIkSC6SBq2eEM4IQXeXlFefKyzH2PFLcgvlzaracem8g5or0wFB+v1EdvAvBISuTM/sK0d+nrCHMFGLm8QjYLQxiiz5y6fsXyKW5dlSL+aT0VXVOYmJ8Vo41zuzCV5g0pmxK0bALN6sgQp/AE5ql12toWZvI1QOexSWQiN0lN8Lj4jhUhbWh5AuR5G1Y+gE4JgG9ei1X5ZRSlAnUTxagHhR9iNzfolwmK8nstjXUe7AuIsRlXl1EKFSVuB+ZB+CzTyamJv/KGlFMm/zTUZJiJTH4IqXYbaWPJUGgWRoSIeKRZNAkf8bLZXShXUe9B/2vlRIXJX+XdDXax1ARIfKGUI74+MFYNrGQD6cYP9XSmshuFwVuLgEhUttCmtSGa0IH1+5xbupaRQQu4w19LdNeyqtBmnkKpUhD1wbpiQZi3GTlc127sG3NYCT0TlklDbZaCV9vowhzJN/zfOSjNOsxfP+C+qdSt4jZ5yE4XOT2gPItnaudxNuxLJ+MxKDwkkdHTNi8qJl3+NXx8DX0h/x24DPcfJOgh/toeKyM9WqpmtVuwv/UZKPF+8cnk/IR5yPhvZ5WmsmS5fwDvBFTB3jVCa19sf1Xdbv3gtBcLZhJ749mT+bsfV6816Tzr+H8e03+BtfBA04k/tP9AAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> вещественные, разные, положительные. Следовательно, точка покоя — неустойчивый узел.
Связь между типами точек покоя и значениями корней характеристического уравнения (2) можно представить наглядно. Для этого введем обозначения . Тогда характеристическое уравнение запишется в виде .
Рассмотрим плоскость с прямоугольными декартовыми координатами и и отметим на ней области, соответствующие различным типам покоя (рис. 42). Из приведенной выше классификации следует, что условиями устойчивости точки покоя являются . Они выполняются при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADUAAAARBAMAAACP9fljAAAAJ1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB+jSoGAAAADHRSTlMAwEURoSHbgmbwMZHLPgtLAAAAy0lEQVQY02NgwA+YF+CWYzmKKcakAKFjjmBKzd4GMczxTAC6XKQCx1QQzTpZxgEswLUVLufDwHAaRHMX6EAtVPSCySUyMIiBaDMDRpiFKkJQxkEGBhkQXc7AdNIAKhYCkeSCyjEnA+kCmGEhGWBnguSAvmAHiutMhrvCPAkmtwBkHQMD43FUOWaomeUgdXALo8FmMkxkYMiEWIewMEQC7j+g2zkmCgJBzmRUP+goMB1iYGA7AwYnwH53gtnKMaOtASUQuVwR7IhWBgYAYb0rVmdybtQAAAAASUVORK5CYII=» /> и 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQCAMAAABncAyDAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMA0GginYExwEIB4FEh8BGxVXXvTAAAAL9JREFUKM+1kdsOAyEIREURvC///7WV3U1bL0nbh/pgonJkhjHmbysGir/U24SY6Pv6IKFDte3eyJf18oC+NbH73xjdbKCy7sLXMftz0TsSBsDJBYj6biBVBBLk9y7IYbDwAhpAMaWimYbmkHMcAZMU8FU9Mq9eHKa8doiCJ7sFYAPQOSonfi1n+5QUbwDuRLquKRIaTRu+cuhqYrJK5SmJYxyryUKatNolwIPpQ3BdQ7KY7qBLmdS4Xf7OZpX9AFDMBpP54cUeAAAAAElFTkSuQmCC» />, т. е. для точек, которые находятся в первой четверти.
Если и комплексные, то точка покоя будет типа фокуса. Этому условию удовлетворяют точки, которые лежат между ветвями параболы и не принадлежат оси .
Точки полуоси , для которых 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADUAAAARBAMAAACP9fljAAAAJ1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB+jSoGAAAADHRSTlMAwEURoSHbgmbwMZHLPgtLAAAAy0lEQVQY02NgwA+YF+CWYzmKKcakAKFjjmBKzd4GMczxTAC6XKQCx1QQzTpZxgEswLUVLufDwHAaRHMX6EAtVPSCySUyMIiBaDMDRpiFKkJQxkEGBhkQXc7AdNIAKhYCkeSCyjEnA+kCmGEhGWBnguSAvmAHiutMhrvCPAkmtwBkHQMD43FUOWaomeUgdXALo8FmMkxkYMiEWIewMEQC7j+g2zkmCgJBzmRUP+goMB1iYGA7AwYnwH53gtnKMaOtASUQuVwR7IhWBgYAYb0rVmdybtQAAAAASUVORK5CYII=» />, соответствуют точкам покоя типа центра.
Точки, расположенные вне параболы 4\Delta)» png;base64,iVBORw0KGgoAAAANSUhEUgAAAKcAAAAZBAMAAACm+CPaAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAb6BKEHnXaEQ0AlxkSizG6IAAAK8SURBVEjHtZVBa9RAFMff7KZmAy0kcYngYdmNpWihYWmwailL6mGpIktR97p0tUXsIUSQpfRQeihWpZYiuPQgYhGhXvoZhOq9B08eBFu79ZTP4HuTpMluWpg9+A5DMvnnN/P+82YG4P+FZDui0vc3RJUz905EpWt3VwWVP2FUUDkwL/8RlC7BxDlf3kUPudnAqOGB43Okd3giyZ7dlCbvUVuZDV83ov7sXEqa5cMdUdtOLM7gl5TychEbxS0Gb/JO1F9Nr2lFpVQ6W2TPx7j79lZaSbisFSZ7wQu7leF0Tj5Bq1YZW/YkLqmDbKrKLIK2Zw6D15Ya9m87z3nGz2Kp7tLH9cbTLiFU7fFeqF4j6E3JD0y9GvW/sa/xCU/G1CkLQVJTJ1NZjbvzwLavj5tXeqFTBYQq87DJTWWPafL7tv3NNAOXlclbUU4lgua8AW6q8RWbt76/GPmQr/OgsfIlgl5ahRovS4msrfidkbjyleWQqjsErarMJVN1GnN0un26sLLNw+FKghoO5P7ymkfo4In2K7mebPlHkBMQdB1ghUzN4G/yMQz97smcrN4Hgi7hHH0nhFbL0JiFLuornj1BpSZOgUzNlLAadyDTPOOEWag3PjtsHh83V0NoxYGVbuh9gma+1/ceQg5TlzvkLUILZTCK6fTzprn3yJOJx00lKB4PL9Qks8X3pG6a7hi00RjmeoGnH7zE8NLpQjGARhGMaY1pOpmqINQE5agr+Wj5KX1bw1hpBtDMQT7eA1oyuUYJWibGCJlKJTUB28X4c1xSoO4xZZGkFh6gBvog7b72zjxzCr5fdn0eZMJLdGvsU5IZF7/lH14MlB10C/Nm0vQ5J5mmghYEGdmiYzDh6FBimzJNZaEUjVbFLxzDE9PxrScaclHwZpjr527cEJO1nX6gOTH1Wn/XuCbmKa7TP6ovmlkrqbjpAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />, соответствуют точкам покоя типа узла.
Область плоскости , где , содержит точки покоя типа седла.
Исключая особые случаи (прохождение через начало координат), замечаем, что седло может перейти в узел устойчивый или неустойчивый (рис.42). Устойчивый узел может перейти либо в седло, либо в устойчивый фокус. Случай равных корней соответствует границе между узлами и фокусами, т.е. параболе .
Пример 2. Исследовать уравнение упругих колебаний с учетом трения и сопротивления среды (при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADEAAAAQBAMAAABNQoq8AAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcGe2BFbQSGBMfCxcU2qjNsAAADDSURBVBjTY2AgDYgvxCHB5WyyALtM9wW2HUhcDgs4006A8TGyyprjAlCWiwCjCpDNekkzACLQrA6RYnwkwKgHZK42DVFghkq5CcBlAhi4NjOwPSuGGtMJlmJ/xMCgV8DA9JSB6yXc8kg3IMEKkelTAOo2gMv4Iuypm8DA+DoArgVkGiPQbdpgGdY3DDAXQP3DAPKPiAFjkRMbiqsZ1iWwPweGkY+RafYxEL8IJsHA5jklAeSShQysIHtYEaHD2JbKwAAA/gYrl5lLD9QAAAAASUVORK5CYII=» />)
Решение. Переходим от уравнения (3) к эквивалентной ему системе уравнений
Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами в математике
Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами
Рассмотрим метод решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами:
Линейной комбинацией функций 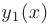
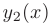
где 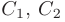
Функции 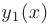
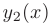
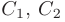
Теорема 7.2. Если 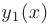
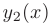
Следовательно, чтобы найти общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, надо знать два его частных линейно независимых решения: 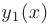
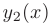
Будем искать частное решение дифференциального уравнения в виде 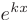
Очевидно, функция 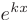
которое называется характеристическиль уравнением исходного дифференциального уравнения.
Как известно, для корней данного квадратного трехчлена возможны три случая.
- Если дискриминант больше нуля
, то корни характеристического уравнения действительные, простые:
- Если дискриминант равен нулю (
= 0), то корни характеристического уравнения действительные, кратные:
- Если дискриминант меньше нуля (
где 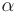
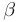
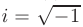
Теорема 7.3. Общее решение 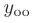
где 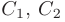
Пример:
Найти частные решения заданных линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами, удовлетворяющие начальным условиям:
► Составим характеристическое уравнение, заменяя в дифференциальном уравнении производные неизвестной функции у соответствующими степенями неизвестного 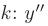
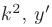
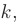
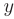
Дискриминант уравнения больше нуля:
В таком случае, корни характеристического уравнения действительные, простые:
Следовательно, общее решение дифференциального уравнения имеет вид
Частное решение получим из общего, используя для определения произвольных постоянных заданные начальные условия:
Решая полученную систему, находим значения произвольных постоянных:
После подстановки найденных значений в общее решение, искомое частное решение принимает вид
► Составим характеристическое уравнение:
Дискриминант уравнения равен нулю:
В таком случае, корни характеристического уравнения действительные, кратные:
Следовательно, общее решение дифференциального уравнения имеет вид
Найдем производную общего решения и определим произвольные постоянные из начальных условий:
Находим значения произвольных постоянных:
и подставим их в общее решение. Искомое частное решение принимает вид
Составим характеристическое уравнение:
Дискриминант меньше нуля:
В таком случае, корни характеристического уравнения комплексно-сопряженные:
Следовательно, общее решение дифференциального уравнения имеет вид
Используем для определения произвольных постоянных заданные начальные условия:
После подстановки найденных значений в общее решение, получим:
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://mathhelpplanet.com/static.php?p=prostyeishie-tipy-tochek-pokoya
http://lfirmal.com/linejnoe-odnorodnoe-differentsialnoe-uravnenie-vtorogo-poryadka-s-postoyannyimi-koeffitsientami-v-matematike/
















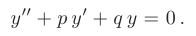
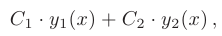
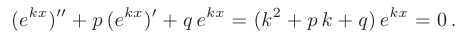
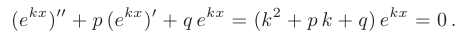
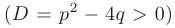 , то корни характеристического уравнения действительные, простые:
, то корни характеристического уравнения действительные, простые: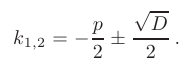
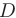 = 0), то корни характеристического уравнения действительные, кратные:
= 0), то корни характеристического уравнения действительные, кратные: