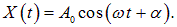Диф уравнение свободных затухающих колебаний

Электронная библиотека

Свободные затухающие колебания – колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения.

Дифференциальное уравнение свободных затухающих колебаний задается в виде:

где – сила сопротивления; s – колеблющаяся величина; d = const – коэффициент затухания; w₀ – циклическая частота свободных незатухающих колебаний той же колебательной системы, при d = 0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы.

Решением уравнения (3.4) в случае малых затуханий является:

где – закон изменения амплитуды со временем; А₀ – начальная амплитуда (при t = 0).

Промежуток времени , в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации.

Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Но, если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся величины.

Период затухающих колебаний равен:

Если A(t) и A(t+T) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение

называется декрементом затухания, а его логарифм – логарифмическим декрементом затухания:

где N_e – число колебаний, совершаемых за время уменьшения амплитуды в е раз.

Для характеристики колебательной системы пользуются понятием добротности (Q), которая при малых значениях логарифмического декремента равна:

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Дифференциальное уравнение затухающих колебаний и его решение

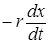
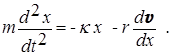
В реальных системах всегда существуют некоторые силы сопротивления, препятствующие развитию колебательных процессов. Для установления характера колебательного движения в этом случае будем считать, что наряду с упругой или квазиупругой силой F_y в системе действует сила трения, пропорциональная скорости и направленная противоположно ей: F_тр = . Тогда учет влияния этих двух сил на характер движения приводит к следующему дифференциальному уравнению:

(8)

Разделив левую и правую части уравнения (8) на m , обозначив r/m = 2b и сохранив обозначение к/m = w₀ 2 , приведем это уравнение к виду:

(9)

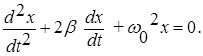
Решение этого уравнения имеет вид:

(10)

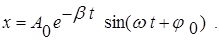
Формула (10) представляет собой смещение при затухающем колебании как функцию времени и параметров системы b и w. Коэффициент b = r/2m имеет смысл коэффициента затухания. Из формулы (10) видно, что в затухающих колебаниях амплитуда уменьшается со временем. Причем, колебания затухают тем быстрее, чем больше коэффициент затухания b. По сравнению с гармоническими колебаниями уменьшается также и циклическая частота колебаний. Это уменьшение зависит от коэффициента затухания. Оказывается, что

(11)

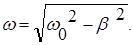
Колебательный процесс может происходить лишь при условии:
(w₀ 2 — b 2 )>0, когда частота w в формуле (11) является действительной величиной . Если же затухание в системе слишком велико (w₀

Дата добавления: 2016-01-20 ; просмотров: 1931 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

1.6. Свободные затухающие колебания

Гармонические колебания, существующие вечно, являются одной из физических абстракций. В реальных системах колебания по прошествии некоторого времени затухают из-за диссипации энергии. Таким образом, представлением о гармонических колебаниях можно пользоваться лишь для времен, малых по сравнению с характерным временем затухания. Затухание колебаний всегда будет наблюдаться в системах с трением.

Уравнение затухающих колебаний

Рассмотрим в качестве примера пружинный маятник, помещенный в вязкую среду. Помимо силы упругости на тело будет действовать сила сопротивления, пропорциональная скорости

где r — соответствующий коэффициент, зависящий от вязкости среды, размеров и формы тела. Поэтому уравнение движения примет вид:

Здесь новый, дополнительный параметр системы, называемый коэффициентом затухания. Колебания незатухающие, если .

Другой пример — электромагнитный контур. Если помимо конденсатора С и индуктивности L в контуре имеется еще и активное сопротивление R, то ЭДС самоиндукции равна сумме напряжения на конденсаторе и падения напряжения на сопротивлении. Поэтому уравнения (1.15) примут теперь вид:

Подставляем первое уравнение во второе:

Напомним, что комбинация L/R уже встречалась нам в теории электромагнетизма, где она характеризовала характерное время затухания (появления) экстратоков замыкания-размыкания. Таким образом, величина b имеет размерность обратного времени, совпадающую с размерностью циклической частоты.

Анализ решений

Итак, в обоих рассмотренных случаях дифференциальное уравнение свободных затухающих колебаний линейной системы имеет вид:

Дифференцируя функцию x(t), получаем:

Подставляем эти выражения в (1.67):

Выражение в квадратных скобках должно быть равно нулю. Замечаем, что в этом выражении сокращаются члены с первой производной . Получаем в итоге дифференциальное уравнение для функции X(t):

Здесь возможны два случая. Пусть сначала . Тогда можно ввести параметр

так что уравнение (1.71) примет вид:

Но это — стандартное уравнение гармонических колебаний, общее решение которого мы знаем:

Значит, мы нашли общее решение уравнения затухающих колебаний (1.67):

Во многих системах коэффициент затухания мал по сравнению с собственной частотой колебаний: . Тогда движение системы можно рассматривать как почти гармоническое колебание с частотой и с амплитудой, изменяющейся по закону (рис. 1.22)

Рис. 1.22. Свободные затухающие колебания

Коэффициент затухания определяет скорость уменьшения амплитуды колебаний: он обратен по величине промежутку времени, за который амплитуда уменьшается в e раз.

Период затухающих колебаний равен:

Пусть первое наибольшее положительное отклонение достигается в момент времени . Последующие наибольшие отклонения того же знака (A’, A», A»’ и т.д. — см. рис. 1.22) образуют геометрическую прогрессию:

Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно:

Это соотношение называется декрементом затухания. Логарифм этого отношения называется логарифмическим декрементом затухания:

Определим количество колебаний, которое совершит система за время . За это время амплитуда уменьшается в е раз, а число колебаний равно:

Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз.

Для характеристики колебательной системы часто употребляется величина, называемая добротностью:

которая пропорциональна числу колебаний N_е, совершаемых системой за то время , за которое амплитуда колебаний уменьшается в е раз. Например, для электромагнитного контура при находим:

Мы видели, что полная энергия в колеблющейся системе пропорциональна квадрату амплитуды. При малом затухании (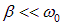) имеем:

где E₀ — значение полной энергии колеблющейся системы в начальный момент времени. Можно определить убыль энергии за период Т:

то есть при слабом затухании добротность, с точностью до множителя , равна отношению полной энергии, запасенной в колебательной системе в данный момент времени, к убыли энергии за один период колебаний.

При увеличении затухания частота колебаний

стремится к нулю, а период колебаний растет. В предельном случае

период обращается в бесконечность, то есть движение перестает быть периодическим. Соответствующий математический анализ показывает, что при движение носит апериодический характер — выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.