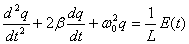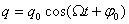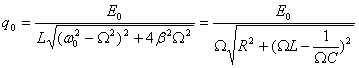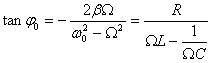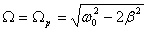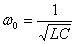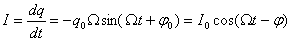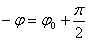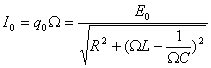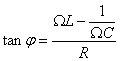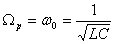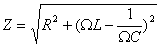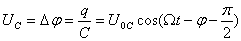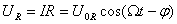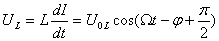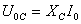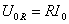Вынужденные колебания
Определение вынужденных колебаний
Для того чтобы в реально существующей колебательной системе получать незатухающие колебания, следует каким-либо образом компенсировать потери энергии, которые происходят в результате существования сил сопротивления. Самым простым способом реализации незатухающих колебаний является воздействие на систему при помощи внешней периодической силы. Работа внешней силы обеспечить приток энергии в систему извне. Эта энергия не даст колебаниям затухнуть, при действии сил трения.
Колебания, которые возникают под действием периодически меняющейся силы (периодически изменяющейся ЭДС), называют вынужденными механическими (электромагнитными) колебаниями.
Дифференциальное уравнение вынужденных колебаний
Допустим, на механическую колебательную систему действует гармонически изменяющаяся внешняя сила:
Рассмотрим колебания груза на пружине (пружинный маятник). Уравнение незатухающих гармонических колебаний для этой системы можно записать как:
где $x$ — координата; $\delta $ — коэффициент затухания; $<\omega >_0$ — циклическая частота свободных незатухающих колебаний (если $\delta $=0, то $<\omega >_<0\ >$называют собственной частотой колебаний).
Если рассматривается, например, электрический колебательный контур, то роль периодически действующей силы может играть внешняя ЭДС или переменное напряжение. Их подводят к контуру извне и изменяются они по гармоническому закону. Уравнение колебаний в электрическом контуре можно представить как:
где $q$ — заряд; $\delta =\frac
Уравнения (2) и (3) можно свести к линейному неоднородному дифференциальному уравнению вида:
где $s$ — колеблющийся параметр; $x_0=\frac
Решением уравнения (4) является сумма общего решения однородного уравнения и частного решения неоднородного уравнения. Однородное уравнение при этом имеет вид:
Его общее решение:
где $A_0$ — начальная амплитуда колебаний.
Частное решение уравнения (4) в представлено выражением:
Слагаемое $s_1$ в решении уравнения (5) играет значительную роль в начальной стадии установления колебаний, пока амплитуда вынужденных колебаний не будет определяться выражением (8).
Установившись, вынужденные колебания происходят с частотой $\omega $ и являются гармоническими. Амплитуда и фаза этих колебаний определяются равенствами (8) и (9), и они зависят от частоты $\omega $.
Резонанс вынужденных колебаний
Если частота вынуждающей силы приближается к собственной частоте колебаний, то возникает резкое увеличение амплитуды колебаний. Такое явление называют резонансом.
Из выражения (8) видно, что амплитуда имеет максимум. Для нахождения резонансной частоты (частоты при которой $A=max$), следует найти максимум функции $A(\omega )$. Взяв производную $\frac
Равенство (10) справедливо при:
Получается, что резонансная частота ($<\omega >_r$) равна:
При $<\delta >^2\ll <\omega >^2_0$ резонансная частота совпадает с собственной частотой колебаний $<\omega >_0.$ Подставим вместо частоты правую часть выражения (11) в формулу (8), получим выражение для резонансной амплитуды вынужденных колебаний:
При небольшом затухании колебаний (если $<\delta >^2\ll <\omega >^2_0$) амплитуда при резонансе равна:
где $Q=\frac<<\omega >_0><2\delta >$ — добротность колебательной системы, величина, характеризующая резонансные свойства колебательной системы. С увеличением добротности увеличивается амплитуда резонанса.
Примеры задач с решением
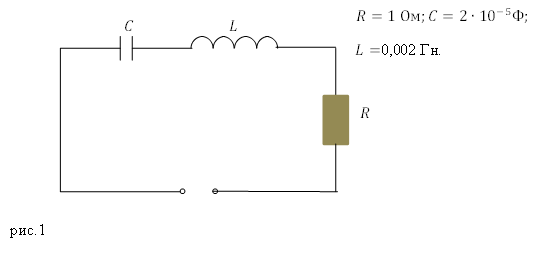
Задание. Какова добротность колебательного контура, представленного на рис.1?
Решение. Добротность электрического колебательного контура найдем как:
При этом собственная частота колебаний в таком контуре равна:
коэффициент затухания находим как:
Подставляет правые части выражений (1.2) (1.3) вместо соответствующих величин в (1.1), в результате, добротность представленного на рис. 1 контура найдем при помощи формулы:
Ответ. $Q=10$
Задание. Пружинный маятник выполняет вынужденные колебания в вязком веществе. Масса груза на пружине равна $m$, коэффициент упругости пружины $k$. Коэффициент сопротивления среды равен $r$. Систему заставляет совершать колебания сила $F=<\cos \left(\omega t\right)(Н).\ \ \ >$Чему равна резонансная амплитуда заданных колебаний ($A_r$)?
Решение. Допустим, что груз совершает колебания вдоль прямой X, тогда уравнением данных механических колебаний будет выражение:
где коэффициент затухания равен $\delta =\frac
мы видим, что амплитуда силы равна единице:
Собственная частота колебаний груза на пружине:
Амплитуда при резонансе таких колебаний равна:
Вынужденные электрические колебания
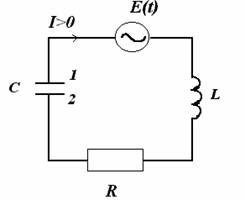
Рассмотрим электромагнитный колебательный контур, в котором помимо ёмкости, индуктивности, сопротивления есть ещё и генератор переменного напряжения, то есть источник электрической энергии. Очевидно, что в таком контуре со временем (это время обычно мало) установятся вынужденные колебания тока с частотой генератора и с постоянной амплитудой; подвод энергии от генератора будет в точности компенсировать потери энергии на сопротивлении.
Не будем учитывать внутреннее сопротивление генератора (будем считать, что у нас хороший, «идеальный» генератор). Получим уравнение для колебаний заряда на обкладках конденсатора. Для этого нам необходимо в закон Ома , который мы писали для затухающих колебаний, добавить в левую часть э.д.с. генератора E(t).
Дифференциальное уравнение вынужденных колебаний заряда в электромагнитном контуре в стандартном (каноническом) виде получается следующим:
или 
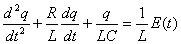
которое полностью аналогично уравнению вынужденных колебаний пружинного маятника . Э.д.с. генератора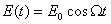 
. Поэтому сразу можем написать решение:
Резонансная частота колебаний заряда на обкладках конденсатора запишется также по аналогии с резонансной частотой механических колебаний маятника:
Напомню, что в электрическом контуре:
и 
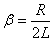
Обратите внимание, что резонансная частота для заряда зависит от коэффициента затухания, а, следовательно, от сопротивления.
Чаще нас интересуют не колебания заряда на конденсаторе, а колебания тока в цепи контура. Найдем эти колебания, продифференцировав заряд по времени:
В этом уравнении сделана подстановка — 
Напомню, что — j является сдвигом фазы между напряжением генератора 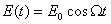и током в цепи. В такой записи знак минус показывает, что напряжение первично, а ток отстает по фазе.
Формулы для амплитуды тока и сдвига фаз выглядят так:
Существенное отличие колебаний тока от колебаний заряда состоит в том, что резонансная частота для тока не зависит от сопротивления; она просто равна собственной частоте свободных колебаний в контуре:
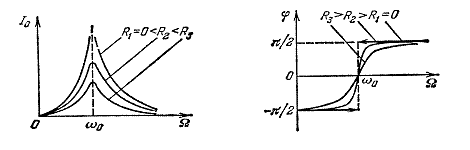
Колебания тока в цепи имеют аналогом не колебания механического маятника, а колебания его скорости. Резонансные кривые для амплитуды тока и зависимость сдвига фаз от частоты для различных сопротивлений — на графиках. Обратите внимание, что при резонансе сдвиг фаз между током и напряжением на генераторе отсутствует.
Посмотрим ещё раз на формулу для амплитуды колебаний тока. В числителе стоит амплитудное напряжение на генераторе (мы пренебрегаем внутренним сопротивлением генератора, поэтому его э.д.с. равна напряжению на его клеммах); в знаменателе — величина, имеющая размерность сопротивления. Она включает в себя не только активное сопротивление R, но и составляющую, зависящую от ёмкости и индуктивности контура и от частоты генератора. Эта величина носит название полного сопротивления контура, или импеданса контура Z:
Величина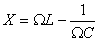 
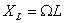
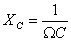
носит название реактивного сопротивления, а её составляющие: 
— индуктивным сопротивлением; 
— ёмкостным сопротивлением.
Посмотрим, как ведут себя колебания тока и напряжения на различных участках контура.
Ток в цепи устанавливается со скоростью распространения электрического поля, то есть со скоростью света с. Время установления тока в цепи
l/c, где l — длина контура. Это время в реальных контурах много-много меньше, чем период колебаний. Поэтому мы считаем, что в каждый момент времени значения тока на всех участках цепи одинаково; колебания тока на сопротивлении, индуктивности и ёмкости происходят синхронно.
Иначе обстоит дело с колебаниями напряжения. Вычислим напряжение на каждом элементе контура и посмотрим, как они отличаются по амплитуде и фазе.
Видно, что напряжение на конденсаторе отстает на четверть периода от напряжения на сопротивлении, а напряжение на индуктивности на столько же по фазе опережает его. Напряжение на ёмкости и индуктивности всегда отличаются по фазе на полпериода. Наглядно сдвиг фаз на элементах цепи можно посмотреть на векторной диаграмме; из неё, в частности, ясно, почему импеданс вычисляется таким образом.
Общее падение напряжения на всех трех элементах цепи равно напряжению на клеммах генератора; поэтому угол j на диаграмме дает сдвиг по фазе между током и напряжением на генераторе.
Дифференциальное уравнение вынужденных колебаний и его интегрирование
Дифференциальное уравнение вынужденных колебаний и его интегрирование
- Чтобы прояснить влияние линейного сопротивления на вынужденную вибрацию, рассмотрим наиболее распространенный случай, когда обобщенная сила Q состоит из трех сил. Потенциал Qn = —dP / dq— —eq, линейное сопротивление b (φ, = −dF / da = — == Hsin (pz + 8). Подставляя это значение обобщенной силы Q = Q «+ Q’t + QB в уравнение Лагранжа (1), aq + \ uj + cq = Hsm (pi + 5). Разделим обе части уравнения на π и введем обозначение k2 = c / a, 2n = c / a, h = Hja. Где A: круговая частота естественной вибрации.
Коэффициент демпфирования, а h относительная амплитуда возмущающей силы. Окончательный вид дифференциального уравнения: q + 2nq + k2q = hs \ n (pt-y8). (44) Линейное дифференциальное уравнение получается с постоянным фактором вынужденной вибрации, который учитывает линейное сопротивление. Поскольку это неравномерное уравнение, решение состоит из двух частей. qx — общее решение для равномерного уравнения. q2 является частным решением неоднородного уравнения. Общее решение однородного уравнения удовлетворяет уравнению для собственных колебаний с линейным сопротивлением.
Но для выявления сил, действие которых испытывает материальная точка, выберем ее собственную систему отсчета, по отношению к которой ее относительные скорость и ускорение равны нулю, т. Людмила Фирмаль
Таким образом, это движение не может быть вибрацией, но называется его собственным движением или вибрацией. Частное решение неоднородного уравнения q2 называется вынужденным колебанием. Общее движение системы характеризуется обобщенной координатой q, равной сумме qt и q2, где q = qt + q2 величина q называется общим вынужденным движением (или вынужденной вибрацией). Общее решение qt для однородного дифференциального уравнения q1 + 2nql + k2qi = 0 может быть выражено в одной из следующих трех форм в зависимости от соотношения между величинами n и k. n k, ql = e «‘(cie’ ^ r2 ‘+ C2 .
В любом из этих случаев qt стремится к нулю с течением времени, то есть затухает из-за наличия коэффициентов e
q. Если коэффициент демпфирования мал (n A) движение не будет колебаться, поскольку затухание очень велико. Следовательно, если через некоторое время возникает линейное сопротивление, суммарное вынужденное движение Людмила Фирмаль
Таким образом, это движение не может быть вибрацией, но называется его собственным движением или вибрацией. Частное решение неоднородного уравнения q2 называется вынужденным колебанием. Общее движение системы характеризуется обобщенной координатой q, равной сумме qt и q2, где q = qt + q2 величина q называется общим вынужденным движением (или вынужденной вибрацией). Общее решение qt для однородного дифференциального уравнения q1 + 2nql + k2qi = 0 может быть выражено в одной из следующих трех форм в зависимости от соотношения между величинами n и k. n k, ql = e «‘(cie’ ^ r2 ‘+ C2e
В любом из этих случаев qt стремится к нулю с течением времени, то есть затухает из-за наличия коэффициентов e
Если коэффициент демпфирования мал (n A) движение не будет колебаться, поскольку затухание очень велико. Следовательно, если через некоторое время возникает линейное сопротивление, суммарное вынужденное движение
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://koi.tspu.ru/waves/ch3_2.htm
http://lfirmal.com/differencialnoe-uravnenie-vynuzhdennyh-kolebanij-i-ego-integrirovanie/