Диф уравнения плоского движения твердого тела

Дифференциальные уравнения плоского движения твердого тела

Для твердого тела, совершающего плоское движение и, следовательно, имеющего три степени свободы, соответственно получим следующие три дифференциальных уравнения:

, , . (179)

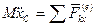
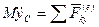
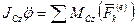
С помощью этих уравнений можно решать две основные задачи: по заданному плоскому движению твердого тела находить действующие на тело внешние силы и по заданным внешним силам и начальным условиям определять его движение. При решении этих задач должны быть заданы масса тела и его момент инерции.

ЛЕКЦИЯ № 8

Теорема об изменении кинетической энергии

Работа силы

Работа силы на каком-либо перемещении является одной из основных характеристик, оценивающих действие силы на этом перемещении.

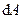
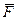
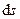
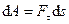
Элементарная работа силы. Элементарная работа силы на элементарном (бесконечно малом) перемещении определяется следующим образом (рис. 54):

, (180)

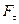
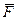
где – проекция силы на направление скорости точки приложения силы или на направление элементарного перемещения, которое считается направленным по скорости точки.

Элементарную работу можно представить, в виде:

, (181)

элементарная работа силы равна произведению элементарного перемещения ни проекцию силы на это перемещение. Отметим частые случаи, которые можно получить из (180):

, ;

, ;

, .

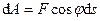
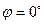
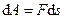
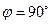
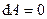
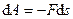
Таким образом, если сила перпендикулярна элементарному перемещению, то ее элементарная работа равна нулю. В частности, работа нормальной составляющей к скорости силы всегда равна нулю.

Приведем другие формулы для вычисления элементарной работы силы:

, (182)

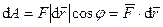
элементарная работа силы равна скалярному произведению силы на дифференциал радиуса-вектора точки приложения силы.

, (183)

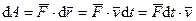
элементарная работа равна скалярному произведению элементарного импульса силы на скорость точки.

Аналитическое выражение элементарной работы:

. (184)

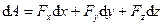
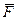
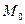
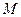
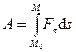
Полная работа силы. Полная работа силы на перемещении от точки до точки равна:

, (185)

Используя другие выражения для элементарной работы, полную работу силы можно представить также в виде

, (186)

, (187)

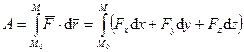
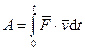
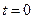
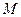
где момент времени соответствует точке , а момент времени – точке .

Из определения элементарной и полной работы следует:

1) работа равнодействующей силы на каком-либо перемещении равна алгебраической сумме работ составляющих сил на том же перемещении;

2) работа силы на полном перемещении равна сумме работ этой же силы на составляющих перемещениях, на которые любым образом разбито все перемещение.

Мощность. Мощность силы или работоспособность какого-либо источника силы часто оценивают той работой, которую он может совершить за единицу времени:

.

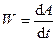
Учитывая определение для элементарной работы, мощность можно представить в виде

.

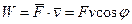
Таким образом, мощность равна скалярному произведению силы на скорость точки.

Дифференциальные уравнения плоского движения твердого тела

Дифференциальные уравнения плоского движения твердого тела

• Используйте теорему о движении центра масс для относительного движения системы к системе и изменения момента движения системы относительно центра масс Рисунок 57 вес тела Для координат, которые постепенно перемещаются в центре тяжести, вы получаете дифференциальное уравнение для плоского движения твердого тела.

Эти пары сил могут быть получены из пар сил, произвольно расположенных в плоскости пересечения путем перемещения в плоскости действия, вращения и одновременного изменения парных плеч и сил. Людмила Фирмаль

Для плоскости движения центра тяжести тела, которое выполняет плоское движение, выберите фиксированную систему координат Oxtylt, которая учитывает движение, и систему Cxu, которая движется вместе с центром тяжести (рисунок 57). Установите xc и yc в качестве координат центра Стационарная система координат. Далее по теореме о движении центра тяжести получены следующие два дифференциальных уравнения для плоского движения твердого тела. Где М — вес.

• Дифференциальное уравнение третьего порядка для плоского движения твердого тела получается из теоремы об изменении момента движения относительно центра масс (38) в проекции на движущуюся ось Cz. dK ^ ldl = LMC2 (F \ e>). Плоское движение твердого тела можно представить как вращение и перемещение относительно центра тяжести C и оси движения Cz. Для вращения вокруг оси момент движения вокруг этой оси рассчитывается как Где со — угловая скорость. JCl — Момент инерции объекта вокруг оси Cz.

Понятия пространства и времени также остаются прежними,и только пространство для принятого понятия инерции должно обладать свойством сопротивляться движению в нем материальных объектов. Людмила Фирмаль

Поскольку JCz является постоянной величиной, подставляя изменение в момент относительного движения в теорему с помощью Kc’g, оно становится следующим. Введение угла поворота ; JCzip = YMCz \ (39) Эти уравнения могут быть использованы для решения двух основных задач. Данное плоское движение твердого тела находит внешнюю силу, действующую на тело, и движение определяется данной внешней силой и начальным условием. При решении этих задач необходимо дать вес L / и момент его инерции.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Дифференциальные уравнения плоского движения твердого тела

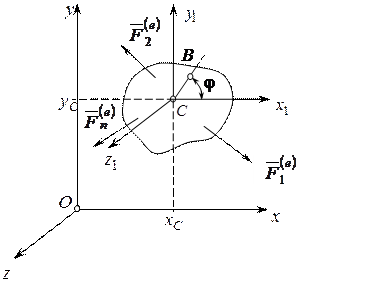
Рассмотрим движение твёрдого тела в плоскости Oxy, под действием системы внешних сил . За полюс примем центр масс этого тела точку С (рис. 18).

Рис. 18. Плоское движение твердого тела

Введём подвижную систему координат Сx₁y₁z₁ в центре масс тела таким образом, чтобы ее оси были параллельны неподвижным осям системы Oxyz.

Плоское движение твёрдого тела рассмотрим как сумму двух движений: движения полюса C (материальной точки) и движения твёрдого тела по отношению к полюсу, которое носит вращательный характер (вращение вокруг подвижной оси Сz₁).

Положение центра масс системы С по отношению к неподвижным осям определяется координатами .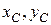

Используя теорему о движении центра масс системы (4.16 / ), получим

,

.

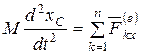
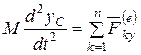
Положение произвольной точки B по отношению к полюсу (центру масс C), в любой момент времени характеризуется углом поворота φ, отсчитываемым от положительного направления оси Ox₁

Используя дифференциальное уравнение вращательного движения твердого тела (4.27), получим

,

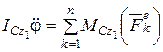
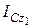
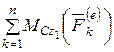
где — момент инерции твердого тела относительно центральной оси Cz₁,

— сумма алгебраических моментов внешних сил относительно центральной оси Cz₁.

Окончательно для твердого тела, совершающего плоское движение (имеющего три степени свободы), получим три дифференциальных уравнения

,

, (4.28)

.

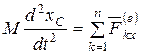
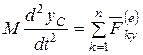
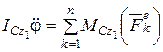
Полученные уравнения (4.28) называют дифференциальными уравнениями плоского движения твердого тела.