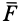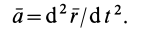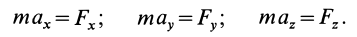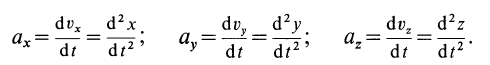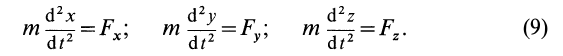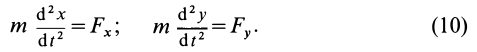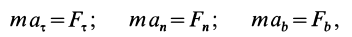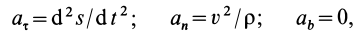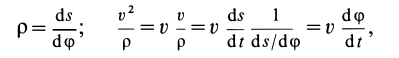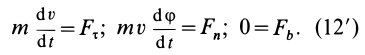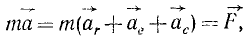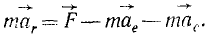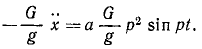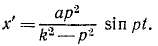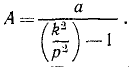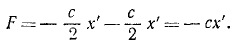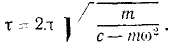Дифференциальные уравнения движения материальной точки в теоретической механике
Содержание:
Дифференциальные уравнения движения материальной точки:
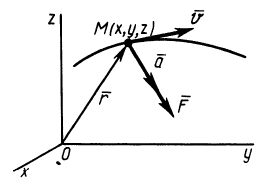
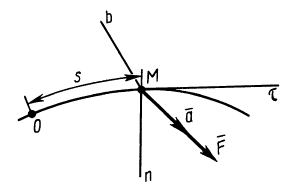
Используя основной закон динамики, можно вывести дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить дифференциальные уравнения движения и несвободной точки так же, как и для свободной, только ко всем приложенным к точке силам надо добавить силы реакций связей.
Силы реакций связей при движении точки могут зависеть в общем случае не только от вида наложенных на точку связей и приложенных к ней сил, но и от характера ее движения, например от ее скорости при движении в воздухе или в какой-либо другой сопротивляющейся среде. В дальнейшем не будем делать различия между свободной и несвободной материальными точками. Обозначая равнодействующую всех заданных сил и сил реакций связей
Из кинематики точки известно, что ускорение 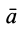
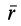
Дифференциальное уравнение движения материальной точки в векторной форме имеет вид
Если спроецировать обе части уравнений (7) или (8) на координатные оси, то можно получить дифференциальные уравнения движения точки в проекциях на эти оси.
В декартовой системе координат в общем случае
Проекции ускорения на координатные оси можно выразить через вторые производные по времени от координат движущейся точки:
Рис. 3
Дифференциальные уравнения движения материальной точки в прямоугольной декартовой системе координат имеют вид
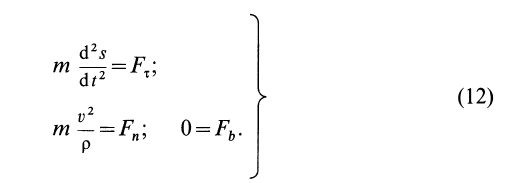
Частные случаи дифференциального уравнения движения материальной точки
Если известно, что материальная точка движется в одной и той же плоскости, то, принимая ее за координатную плоскость 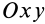
Так как 
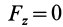
Так как при движении 
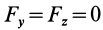
где 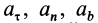
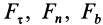
где 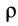
Второе уравнение из (12) можно преобразовать:
где 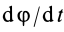
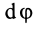
Дифференциальные уравнения (12) можно представить в виде
Рис. 4
Эта форма дифференциальных уравнений движения точки удобна при исследовании некоторых случаев полета снарядов и ракет, особенно по траектории, лежащей в плоскости. Тогда 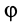
Дифференциальные уравнения движения точки можно представить в любой другой системе координат. Для этого надо знать выражения проекций ускорения на эти оси координат.
Дифференциальные уравнения относительного движения точки
Кориолисовыми силами инерции называют две векторные величины, имеющие размерность силы и добавляемые к силам, приложенным к материальной частице, для определения ее относительного ускорения
Все дифференциальные уравнения движения, с которыми мы ознакомились в этой главе, относятся к абсолютному движению, т. е. к движению по отношению к инерциальной системе отсчета. Для написания дифференциальных уравнений движения точки (или частицы) относительно подвижных осей подставим в основное уравнение динамики (123) вместо абсолютного ускорения точки его выражение (110):
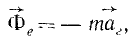
имеющую размерность силы, равную произведению массы материальной частицы на ее переносное ускорение и направленную противоположно этому ускорению, называют переносной силой инерции Кориолиса.
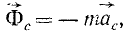
равную произведению массы материальной частицы на ее кориолисово ускорение и направленную противоположно этому ускорению, называют поворотной силой инерции Кориолиса.
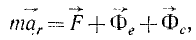
или в проекциях на оси координат:
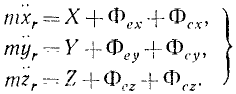
Таким образом, относительное движение материальной точки можно описать такими же (по форме) дифференциальными уравнениями, как и абсолютное, но к действующим на точку силам нужно прибавить две кориолисовы силы инерции: переносную и поворотную.
Эти величины следует отличать от даламберовых сил инерции (см. гл. XX), введение которых позволяет решать задачи динамики методом статики.
Пример решения задачи №1
Определить амплитуду вынужденных колебаний в относительном движении вибрографа для записи вертикальных колебаний фундамента (рис. 171), совершающего вместе с фундаментом колебания по закону χ = a sin pt, если вес груза равен G и жесткость пружины с.
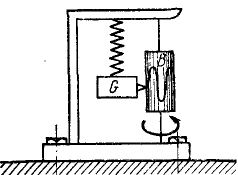
Рис. 171
Решение. Рама жестко соединена с фундаментом и участвует в его колебаниях, как и вращающийся барабан В, на котором груз G, перемещаясь вверх и вниз, записывает колебания фундамента. Вертикальные перемещения х’ груза G по отношению к раме являются относительными и по отношению к барабану, если пренебречь его вращением. Уравнение этих относительных перемещений можно составить как уравнение абсолютного движения, если к заданным силам добавить переносную кориолисову силу, равную и противоположную произведению вектора переносного ускорения на массу груза. Переносная сила инерции груза равна
Напишем дифференциальное уравнение относительных колебаний груза, сократив на m:
x’ + k 2 χ’ = ар 2 sin pt.
где 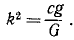
Амплитуда этих колебаний тем менее отличается от амплитуды колебаний фундамента, чем меньше собственная частота k прибора сравнительно с частотой р, т. е. чем меньше жесткость пружины и чем больше масса груза.
Ответ.
Пример решения задачи №2
Ползун G (рис. 172) может скользить по хорде AB равномерно вращающегося горизонтального диска, к точкам А и В которой он прикреплен двумя одинаковыми пружинами жесткостью 
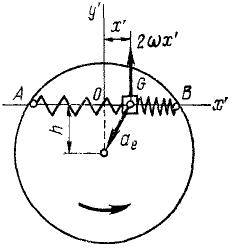
Рис. 172
Решение. Построим оси подвижной системы координат с началом в точке О (в положении относительного равновесия ползуна), направив Ox’ но хорде.
Определим силы, действующие на ползун. Если ползун отклонится от равновесного положения О на величину х’, то одна из пружин сожмется, а другая растянется. Согласно закону Гука сила каждой из пружин пропорциональна деформации х’ и направлена к точке О. Следовательно, на ползун действует активная сила
Кроме активной силы, надо учесть действие кориолисовых сил: Φe—переносной и Φc-поворотной.
Переносная сила инерции равна произведению массы т ползуна на его переносное ускорение: 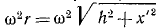
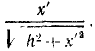
Поворотная сила Кориолиса равна произведению массы ползуна иа кориолисово ускорение 2ωx’ и направлена против этого ускорения. Таким образом, чтобы определить направление поворотной силы Кориолиса, надо вектор относительной скорости повернуть на 90° против переносного вращения. Находим, что поворотная сила инерции действует перпендикулярно AB и проекция ее на Ox’ равна нулю.
При найденных значениях активных сил и кориолисовых сил дифференциальное уравнение относительного движения ползуна по хорде имеет вид:
mх’ = — cx’ + mω 2 x’= — (с—mω 2 )x’.
Это уравнение выражает гармоническое колебание с периодом
Ответ. 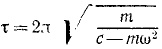
Пример решения задачи №3
Составить дифференциальное уравнение относительного движения ползуна, описанного в предыдущей задаче, считая, что при его движении вдоль хорды AB возникает трение, пропорциональное нормальному давлению на хорду.
Решение. Нормальное давление обусловлено поворотной силой инерции и нормальной составляющей переносной силы инерции.
Поворотная сила ползуна Φс=2mωx’ переменна по величине и направлению. Она направлена перпендикулярно к хорде AB, но в сторону положительных значений у’, если точка G движется в сторону отрицательных значений х’, т. е, если х’ 2 h. Эта составляющая в рассматриваемом механизме всегда направлена в сторону положительных у’, а потому в суммарном давлении обе кориолисовы силы складываются при х’ 0, и дифференциальное уравнение относительного движения точки имеет вид
mх’ =— (с—mω 2 ) x’ — fm (2ωx’ ± ω2h),
причем знак второго слагаемого в скобках надо брать положительным при х’ 0. Решение такого уравнения при движении точки G влево и вправо получается, конечно, различным. Если Л — 0 и хорда является диаметром, то вместо кулонова трения получается вязкое демпфирование, зависящее от скорости.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
ДВИЖЕНИЕ ЧАСТИЦ В ВОЗДУШНОМ ПОТОКЕ
Автор: A.A. Соболев, H.A. Мельников, Л.О. Тютюнник
Источник: Тольяттинский государственный университет. Вектор науки ТГУ. №3(17), 2011 — c. 82–86.
Ключевые слова: движение частиц; воздушный поток; лобовая сила; адгезия; подъемная сила; сила трения; уравнение движения частиц.
Аннотация: Проанализbрованы силы, действующие на частицу в воздушном потоке, составлено уравнение, которое описывает траекторию движения частицы на разгонном участке, построен график зависимости подъема частицы от горизонтального пробега на разгонном участке, описан процесс отрыва частицы от поверхности.
Твердые частицы. неподвижно лежащие иа поверх по¬ети, иод действием веаеыватошего воздушного потока могут двигаться но поверх и о ста, отрываться от неё и переходить в азрорированное состояние. Частицы при определенной кри-тической скорости воздуха начинают трогаться, потом дви¬гаться ускоренно и в последствии могут достигнуть постоян¬ной скорости νk=const.
Начальный участок пути, где скорость частицы увеличивается от ν0=0 до νk=const называется разгонным участком. Здесь частицы движутся с ускорением.
Для нахождения аналитических зависимостей параметров процесса движения и отрыва частиц от поверхности допускаем некоторые упрощения. Считаем, что частицы движутся одиночно, имеют форму шара, движение происходит в неограниченном пространстве, а воздушный поток постоянный по скорости и направлению.
Длина разгонного участка зависит от аэродинамических свойств частиц, их скорости витания и критической скорости, от параметров воздушного потока, его скорости, плотности воздуха и от состояния и материала поверхности.
ДЕЙСТВУЮЩИЕ СИЛЫ НА ЧАСТИЦУ В ВОЗДУШНОМ ПОТОКЕ
На неподвижную частицу в воздушном потоке действует сила веса, сила давление потока, сила адгезии, подъемная сила и сила трения.
Fp — равнодействующая сила, Н;
P — вес частицы, Н;
Fдав — сила давления потока (лобовая сила), Н;
Fад — сила адгезии,Н;
Fпод — подъемная сила, Н;
Fтр — сила трения частицы о поверхность, Н.
Лобовая сила
При обтекании частицы воздушным потоком возникает сила давления (лобовая сила), под действием которой происходит ее движение в горизонтальном потоке.
Величину силы давления воздушного потока на частицу можно рассчитать по формуле [1]:
c — коэффициент сопротивления частицы;
ρ — плотность воздуха, кг/м 3 ;
S — миделевое сечение частицы, м 2 ;
u — средняя скорость воздушного потока, м/с.
Сила воздействия воздушного потока на частицу пропорциональна второй степени средней скорости воздушного потока, т.е. F
U 2 , поэтому по мере уменьшении скорости воздушного потока сила, воздействующая на частицу, уменьшается в квадрат раз. Например, при уменьшении скорости в 3 раза воздействующая сила потока на частицу уменьшается в 9 раз. По этой причине втягивание частиц с поверхности по мере удаления от входной щели заборного насадка сильно уменьшается и на расстоянии 10–15 мм практически совсем прекращается.
СИЛЫ АДГЕЗИИ
Адгезия (прилипание) возникает при соприкосновении тел и является результатом молекулярного взаимодействия, которое проявляется при непосредственном контакте частиц между собой и поверхностью. Взаимодействие частиц между собой называют аутогезией, а взаимодействие частиц с твердой поверхностью называют адгезией. Сила адгезии зависит от площади контакта частиц с плоской поверхностью, так как молекулярное взаимодействие пропорциональны площади контакта. Силы аутогезии определяются формой и состоянием поверхности частиц.
Отрыв от поверхности прилипшего слоя мелкого материала воздушным потоком происходит следующим образом. Сначала отрываются верхние более крупные частицы, потом отрываются мелкие частицы, т.е. преодолеваются силы адгезии слоя. Удаление верхних частиц возможно при Fад>Fаут. Аутогезионный процесс отрыва частиц называется эрозией. При Fад -10 м сила адгезии максимальна и равна
Силы адгезии убывают пропорционально квадрату размера зазора. Поэтому мелкие частицы (порядка менее 50 мк) имеют большую площадь соприкосновения, по отношению с размером крупной частицы, и их величина силы адгезии больше чем, у крупных частиц. По этой причине для отрыва более крупных частиц от поверхности необходима меньшая сила, чем для подъема мелких частиц, менее 50 мк.
Под действием градиента скорости силы трения отличаются по величине на противоположных сторонах частицы, что порождает возникновению крутящего момента. Влияние градиента скорости возрастает для более крупных частиц. Под действием момента сил, когда равнодействующая сила не проходит через центр тяжести частицы, возникает вращение частиц дисперсного материала. Для округленных частиц эта сила не играет большой роли. Одной из причин вращения округленных частиц в воздушном потоке является столкновение с поверхностью и другими частицами. Вращение частиц под действием градиента скорости и столкновение с поверхностью и другими частицами происходит вокруг оси, которая лежит в плоскости, нормальной к направлению потока.
Угловая скорость вращения частиц зависит от изменения скорости потока по нормали к поверхности, т.е. градиента скорости потока, равно:
α — угловая скорость вращения частицы, рад;
du/dy — градиент скорости потока, с -1 .
Неравномерная скорость обтекания и вращения частиц вызывает циркуляцию воздуха по контуру частицы. Если направление скорости потока и вращение частиц совпадают, то скорость течения увеличивается, а со стороны, где они противоположны — уменьшается. По этой причине под частицей давление возрастает, а над частицей — уменьшается, благодаря этому возникает сила, действующая на частицу снизу вверх.
Pд — давление воздушного потока, Н/м 2 ;
На частицу сверху вниз будет действовать сала равная dF1=P1S, а снизу вверх dF2=Pд2S, где Pд1 и Pд2 давление на частицу соответственно сверху и снизу.
Направление этой силы всегда направлено к той стороне вращающей частицы, на которой вращение и потока совпадают.
Неравномерная скорость обтекания частиц и вызванная циркуляция воздуха по контуру частицы порождает эффект Магнуса и создает силу, действующую на частицу в перпендикулярном к направлению потока и называется поперечной или подъемной силой, или силой Магнуса.
Величина этой силы в соответствии с теорией Н.Е. Жуковского может быть выражена следующем образом:
k — коэффициент трения.
ux — средняя скорость воздушного потока, м/с.
Таким образом, величина циркуляции, а следовательно, и подъемная сила определяются в основном градиентом скорости по поперечному сечению потока. Увеличение градиента скорости i=dv/dy ведет к увеличению подъемной силы. Подъемная сила является главной причиной отрыва частиц от поверхности.
СИЛА ТРЕНИЯ
Силу трения между частицей и плоскостью можно записать следующим образом:
k — коэффициент трения.
После того как сила давления воздушного потока на частицу превысит силу трения, возникает скольжение ее по поверхности. Сила трения всегда направлена противоположно перемещению частицы.
УРАВНЕНИЕ ДВИЖЕНИЯ ЧАСТИЦЫ
Дифференциальное управление движения частицы, принимаемой за точку, на разгонном участке в плоском горизонтальном воздушном потоке имеет вид:
(d 2 l)/(dt 2 )=(dv)/(dt) — ускорение движения частицы, м/с 2 .
Под действующей равнодействующей силы частицы будут отрываться от поверхности и всасываться в заборное устройство.
Спроектируем равнодействующую силу (12) на оси прямоугольной системы координат. За начало отсчета примем точку начала движения частицы в потоке. Ось ординат направим вертикально вверх, а ось абсцисс по направлению движения воздушного потока. Тогда будем иметь:
d 2 y/dt 2 и d 2 y/dt 2 — проекции ускорения частицы на оси X и Y.
Fx и Fy – проекции силы на соответствующие оси координат;
X и Y – соответствующие координаты движущейся частицы;
Рис. 1. Силы, действующие на частицу.
Под действием силы Fx частицы будут двигаться в горизонтальном направлении, а под действием силы Fy в вертикальной плоскости.
Проекции сил на ось Y: Fпод≠0, P≠0, Fад≠0
Таким образом, в горизонтальной плоскости на частицу действует сила давления воздушного потока (лобовая сила) и сила трения, а в вертикальном — сила веса, подъемная сила и сила адгезии.
Условия, при котором возможен перенос частицы в горизонтальной плоскости скольжением, волочением или перекатыванием выразится следующим неравенством:
Условия, при котором возможен унос частиц с поверхности, выразится неравенством:
Подставив в формулы (15) и (16) выражения, получим систему уравнений:
q – ускорение силы тяжести, м/с 2 .
Упростив и решив систему уравнений (19), получим:
Полученная система уравнений (20) описывает траекторию движения частицы на разгонном участке.
Рис. 2. График зависимости подъема частицы линейным размером 0,001 м. от горизонтального пробега на разгонном участке при скорости воздушного потока V0: 1–50 м/с, 2–40 м/с, 3–30м/с,4–20м/с.
На рис. 2 представлен график зависимости подъема от горизонтального пробега частицы на разгонном участке при скоростях воздушного потока во входе в щель заборного устройства 50; 40; 30; 20 (м/с), представляющий прямые линии с углом наклона, ? в зависимости от скорости воздушного потока при входе в щель насадка.
Преобразовав систему уравнений (20), получим:
Из уравнения (21) следует, что путь частицы в горизонтальном направлении под действием воздушного потока прямо пропорционально пути в вертикальном направлении, т.е. x =f·y,где:
f = 0,93÷0,99 — опытный коэффициент пропорциональности.
Т.к. x/y=ctgα , то x=y·ctgα, тогда
Формула (23) дает возможность теоретически определить угол наклона прямых, описывающих траекторию частицы в зависимости от скорости воздушного потока.
На рис. 3. и 4. представлен график расстояния переноса частицы воздушным потоком относительно вертикального и горизонтально направления в зависимости от времени.
ОТРЫВ ЧАСТИЦ ОТ ПОВЕРХНОСТИ
Явление отрыва частиц от поверхности произойдет тогда, когда скорость воздушного потока достигнет критической скорости. При увеличении скорости потока частицы будут в массовом порядке отрываться и переходить в аэрорированное состояние.
Рис. 3. График переноса частицы на ось X в зависимости от времени 1–50м/с;2–40м/с;3–30м/с;4–20м/с.
Отрыв частиц от поверхности начинается со скольжения или перекатывания.
Удаление сыпучего материала с поверхности воздушным потоком достигается в результате силового воздействия потока. Адгезиционная сила Fад действует только во время отрыва частиц от поверхности. После отрыва частицы от поверхности при Fпод ≥ P перейдут в аэрорированное состояние.
При Fпод Fаут. Аутогезионный процесс отрыва частиц называется эрозией. При Fпод Fаут нужно различать 2 скорости воздушного потока: первая из них характеризует условия, при которой преодолеваются силы аутогезии. Величина первой скорости всегда меньше второй.
При условии Fад Fотр > Fаут — аутогезионный процесс отрыва. При Fад = Fаут возможен смешанный аутогезионно–адгезационный отрыв частиц.
Рис. 4. График переноса частицы на ось Y в зависимости от времени 1–50м/с;2–40м/с;3–30м/с;4–20м/с.
Полуенные зависимости параметров движения частиц от характеристики величин пылегазового потока, являются основой для расчета сдувания частиц с поверхности, вакуумной пылеуборки и т.д.
Процесс отрыва частиц от поверхности осуществляется следующим образом. Под воздействием воздушного потока сначала происходит сдвиг или качение частиц, потом скольжение или перекатывание, затем отрыв и переход в аэрированное состояние. При этом аэродинамическая подъемная сила должна преодолеть вес частицы и силу аутогезии между частицами, то есть:
силы прилипания при прочих равных условиях пропорциональны линейным размерам частиц Fад
l, а вес частицы пропорционален линейному размеру в третьей степени P
l 3 . Следовательно с уменьшением размера частиц роль прилипания возрастает. Для частиц менее 50 мк, силы адгезии значительно превышают вес частиц. Поэтому крупные частицы диаметром более 50 мк эффективнее удаляются с поверхности, так как P > Fад.
Затраты энергии на разгонном участке. Для достижения частицей на разгонном участке равномерной скорости от v0=0 до vk=const необходимо затратить большое количество энергии [2,3].
Движение частиц, перешедших во взвешенное состояние, происходит с ускорением и в пределе достигает постоянной скорости, которая всегда меньше скорости движения воздуха. Эта разность скоростей и дает возможность двигаться частицам:
где E — кинетическая энергия частицы, Дж;
vk — постоянная скорость частицы, м/с.
Кинетическая энергия частиц возникает за счет передачи энергии воздушного потока частицам. При этом можно определить скорость движения частицы в зависимости от скорости воздушного потока.
В вертикальном потоке разность между скоростями восходящего потока и частицы примерно равно ее скорости витания.
При удалении пыли с воздухонепроницаемой поверхности требуются более значительные скорости движения воздуха, чем транспортировка ее.
Для перевода из состояния покоя в движение со скоростью vk частиц материала массой m, необходимо затратить энергию равную (m vk 2 )/2 = E.
Для получения такой энергии необходим объем воздушного потока L, м 3 при давлении Pд, то есть (m vk 2 )/2 = LPд, отсюда:
где L — объем воздушного потока, м 3 .
Таким образом, для придания частице скорости v массой m необходим воздушный поток объемом L при давлении Pд.
Затраты энергии на разгонном участке частицы можно найти из уравнения момента количества движения [1]:
где F — сила воздушного потока, H.
При интегрировании этого выражения в пределах времени от t0=0 до t, скорость частицы изменяется от 0 до vr, получим m vr = F t.
После преобразований получим:
После интегрирования получим:
Таким образом, получено уравнение для расчета потери энергии воздушного потока на разгон частиц.
http://masters.donntu.org/2014/fimm/mitina/library/article7.htm